战斗部约束条件下的立方体反导破片优化设计

陈 洋，董桂旭，宋之勇，杜茂华

（1.海军驻重庆地区导弹设备军事代表室，重庆 402760；2.海军航空工程学院研究生管理大队，山东 烟台 264001）

随着战术巡航导弹、空地导弹、制导炸弹等攻击性精确制导武器的飞速发展，反导技术已成为各国防空反导领域的热点课题。根据各国制导精度水平的差异，目前采用的反导毁伤技术主要有两种形式：一是以美国“爱国者-3”型为代表的直接碰撞技术，一是以俄罗斯“C-300”、“C-400”系列为代表的破片杀伤技术。前者毁伤概率较高，但对制导技术的要求极高，只有美国等极少数国家掌握；后一种对制导技术的要求相对较低，但对战斗部的毁伤能力要求极高。在制导水平不能于短期内得到较大提高的条件下，破片式反导仍将成为未来一段时期内的主要反导模式[1]。在破片式反导中，反导破片的设计直接影响到战斗部综合性能的提升，意义十分重大。国内外很多专家学者对破片式反导开展了多方面的研究[2-4]，本文重点对给定战斗部约束条件下的立方体反导破片优化设计方法开展研究，以使得战斗部的破片平均初速、破片密度、单枚破片毁伤能力等综合性能达到最优。

1 研究模型

1.1 基本假设

本研究基于以下假设：

1)破片形状为立方体，贴向主装药的截面为正方形，为非含能材料制成；

2)战斗部预留一定的空间装填破片，其余参数不变；

3)以来袭导弹的战斗部为毁伤目标，并将目标战斗部等效成带一定厚度钢板屏蔽的炸药；

4)只考虑单枚破片对目标的毁伤作用，而不考虑多枚破片命中时的叠加作用；

5)以破片既能够击穿目标的屏蔽钢板，又能够引爆被屏蔽的炸药作为毁伤判据；

6)在同样约束条件下，单枚破片能够毁伤目标，且破片装填数量最多。

1.2 反导破片是否具备毁伤能力的判定方法

先随机给出一组战斗部基本参数，预留一定的空间装填破片。在战斗部其他参数不变的情况下，仅变化破片材料、破片底面边长，并计算不同条件下的破片数量、平均初速、着靶速度、对目标靶板的穿透能力、对目标靶弹的引爆能力等，分别判定单枚破片设计是否满足既能穿透靶板又能引爆目标装药的判据要求，最终输出所有符合要求的反导破片基本参数。

1.3 基本公式

单枚破片对一定厚度钢板屏蔽的炸药以一定速度入射，当入射速度达到一定临界值时(称为速度阈值)，主装药将被引爆，速度阈值可按式(1)计算[5]：

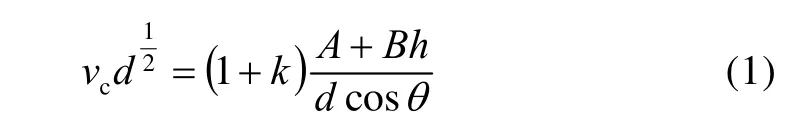
式(1)中：vc为速度阈值(km/s)；d为破片等效截面直径(mm)；h为壳体等效厚度(mm)；θ为破片轴线相对于靶板碰撞点法线的夹角；A、B为材料系数，对B 炸药，A=3.33，对低碳钢靶板，B=5.34。

工程上往往采用式(2)计算破片对靶板极限穿透速度[6]。

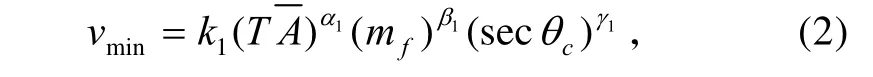
式中：对低碳钢 k1为5791；T为靶厚(cm)；为破片平均着靶面积(cm2)；1α为0.906；1β为0.963；1γ为1.286；mf为破片质量(g)；cθ为破片着角。

破片平均初速按式(3)进行计算。

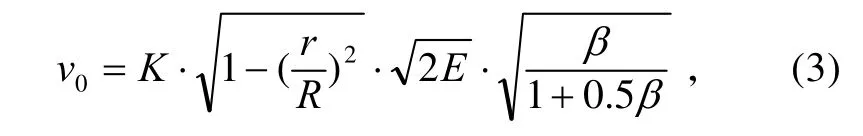
式中：v0为破片平均初速(m/s)；r为装药内径(mm)；R为装药外径(mm)；h为壳体等效厚度(mm)；K为公式计算修正系数；为格尼能；β为装药质量比。

破片存速可用公式(4)计算[7]：

式(4)中：vr为距离r 处的存速(m/s)；v0为破片平均初速(m/s)；α为衰减系数(1/m)。

α可用式(5)进行计算[6]：

式(5)中：CD为气动阻力系数，对球体取0.97，对正方体取1.24；aρ为当地空气密度(kg/m3)；S为破片展现面积，对规则形状的物体取表面积的四分之一(m2)；mf为破片质量(kg)。

2 反导破片的优化设计

2.1 破片层厚度不变条件下的优化设计

按以上方法，利用VB 编程进行计算，计算流程图见图1。

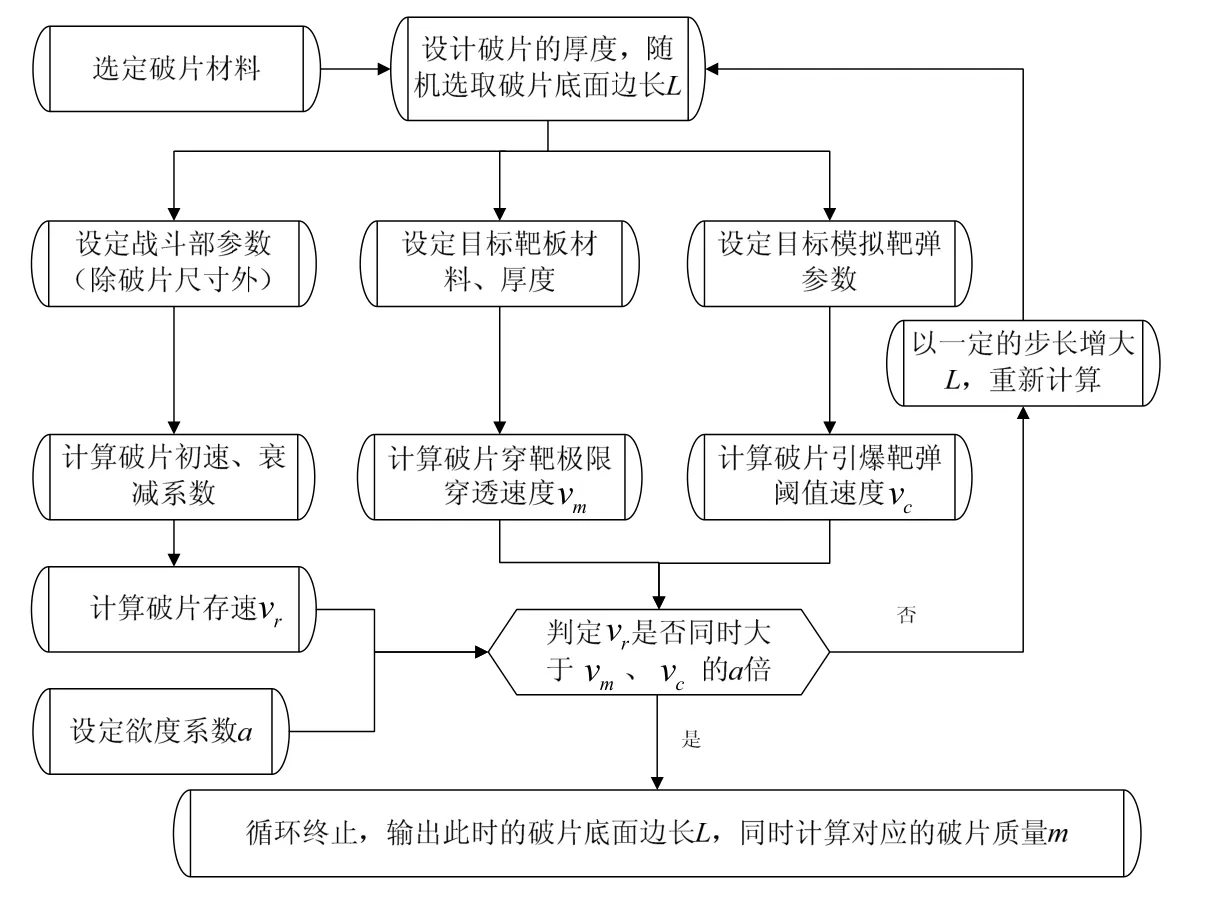
图1 破片层厚度不变条件下的优化设计流程

以φ203口径定向战斗部为例，预设一组参数(见表1)，按图1中的流程，首先计算破片层厚度h 固定的条件下，仅变化破片边长，满足条件的最小破片质量。以h=6.4mm，钢破片为例进行计算，结果见图2。

表1中速度增益是指定向战斗部在目标方位产生的初速增益，是与中心起爆相比得出的结果；裕度系数1.05是指破片的着靶速度必须同时不小于此种破片对目标靶弹钢板的极限穿透速度 vm和破片引爆目标装药的阈值速度 vc的1.05 倍。

由图2可知，当破片底面边长L 取不小于16.7 mm时，破片才能满足合格判据要求，此时破片尺寸为6.4 mm×16.7 mm×16.7 mm，若将横坐标转换成对应的破片质量，得到图3所示的曲线。

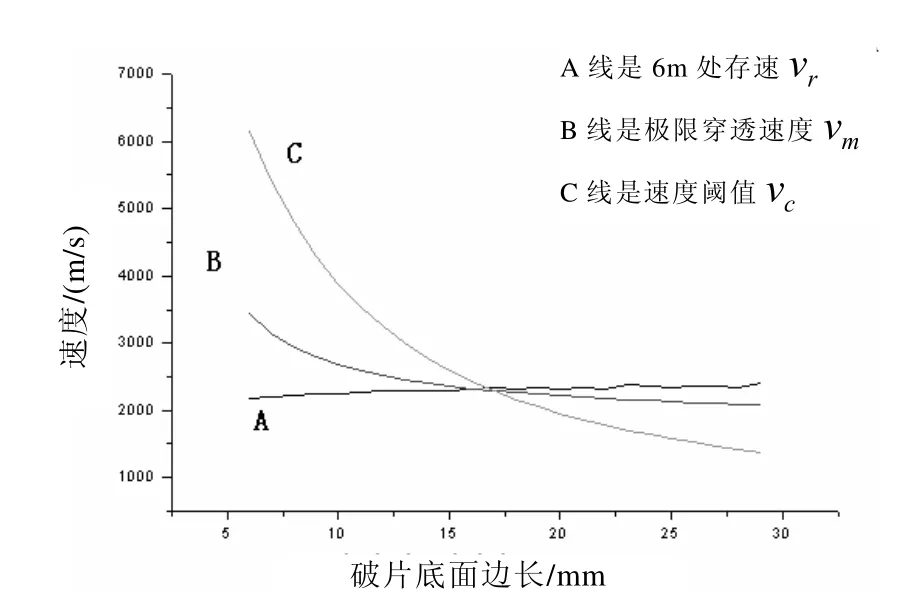
图2 h=6.4 mm时破片边长变化与各种速度值关系(钢)

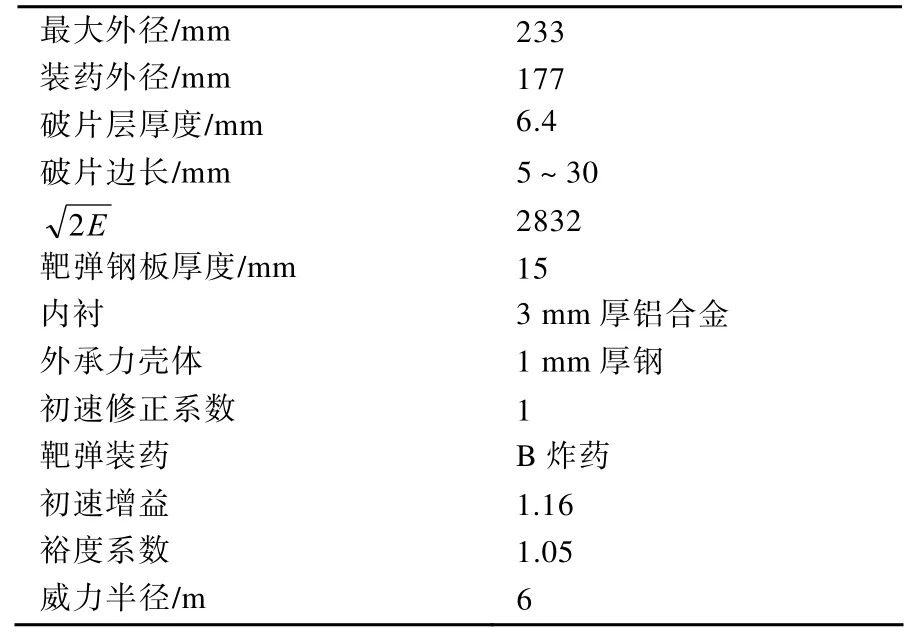
表1 战斗部参数取值

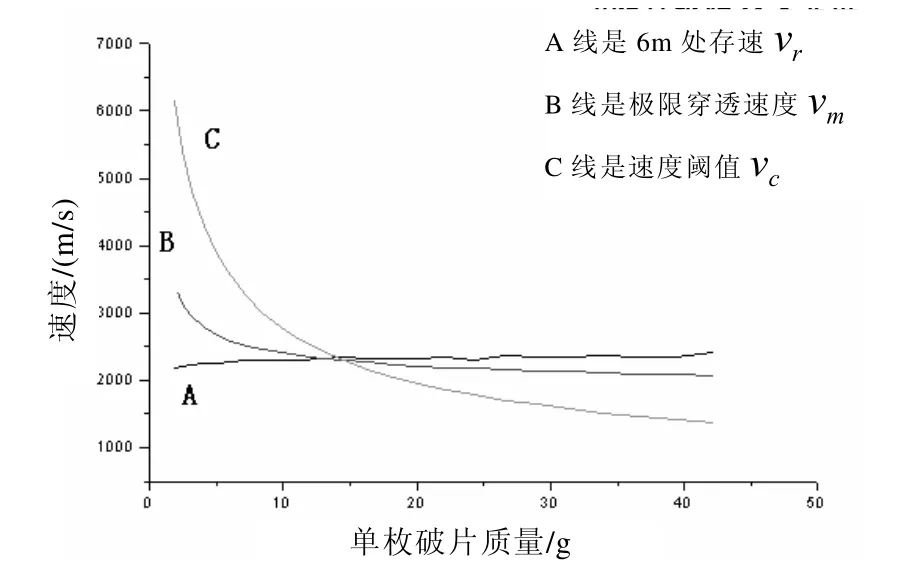
图3 h=6.4 mm时破片质量变化与各种速度值关系(钢)

由图3可见，当单枚破片质量取14.01 g时，Vγ首次满足要求，故在该模型中，破片层厚度取6.4 mm时，单枚破片质量最小为14.01 g 才满足要求，此时破片尺寸为6.4 mm×16.7 mm×16.7mm，破片材料为钢。

同理，可计算破片材料为钨，层厚度为6.4 mm时的破片最小质量，同时与钢破片对比，如图4所示，可见，对钨破片，破片层厚度取6.4 mm时，单枚破片质量最小为45 g 才满足要求(A 线与C 线交界处)，此时破片尺寸为6.4 mm×20 mm×20mm。

根据以上计算结果可见，破片厚度恒定条件下，用钨破片比用钢破片要具备更大的尺寸，即更大的重量。

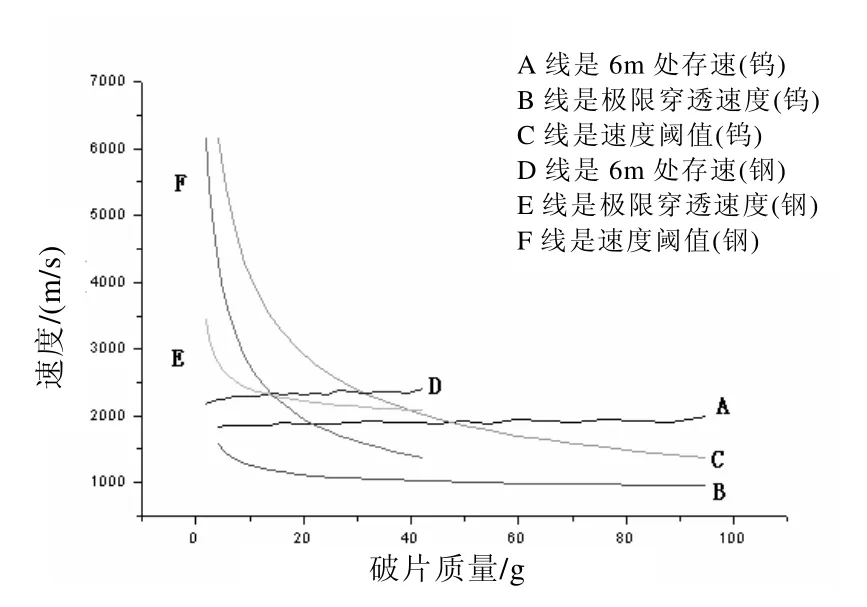
图4 h=6.4 mm时破片质量变化与各种速度值关系(钢、钨对比)

2.2 破片层厚度变化时反导破片的优化设计

根据以上计算方法，每给定一个破片层厚度，均可优化计算出对应的最小破片质量，若给破片层厚度设定一定的可用范围，则根据图5中的流程，进行循环嵌套，同样可计算出满足合格判据的最小破片质量。假设破片层厚度在5～9 mm 间变化，按图5中的流程，分别计算钢、钨破片需要的最小破片质量，结果见图6。

由图6可知，在其余约束条件不变，破片层可用厚度为5～9 mm时，对钢破片，最小破片质量为13.57 g，对应破片尺寸为6.2 mm×16.7 mm×16.7 mm；对钨破片，最小破片质量为33.08 g，对应破片尺寸为5.1 mm×19.2 mm×19.2mm。

3 工程应用中应考虑的其他影响因素

3.1 破片厚度与底面边长之比的影响

对于立方体破片，当破片厚度与底面边长之比λ过小时，破片呈扁平状，在爆轰驱动条件下的破碎率较高，将极大降低破片的毁伤能力，在一般的工程应用中，λ 应不小于0.5。而根据3.2计算的结果，对6.2 mm×16.7 mm×16.7 mm的钢破片和5.1 mm×19.2 mm×19.2mm的钨破片，λ分别为0.37、0.27，显然不满足要求，故应在图6所示的计算结果中，按λ不小于0.5 对破片进行二次筛选。将图6中的横坐标转换成对应的λ，得到图7所示的结果

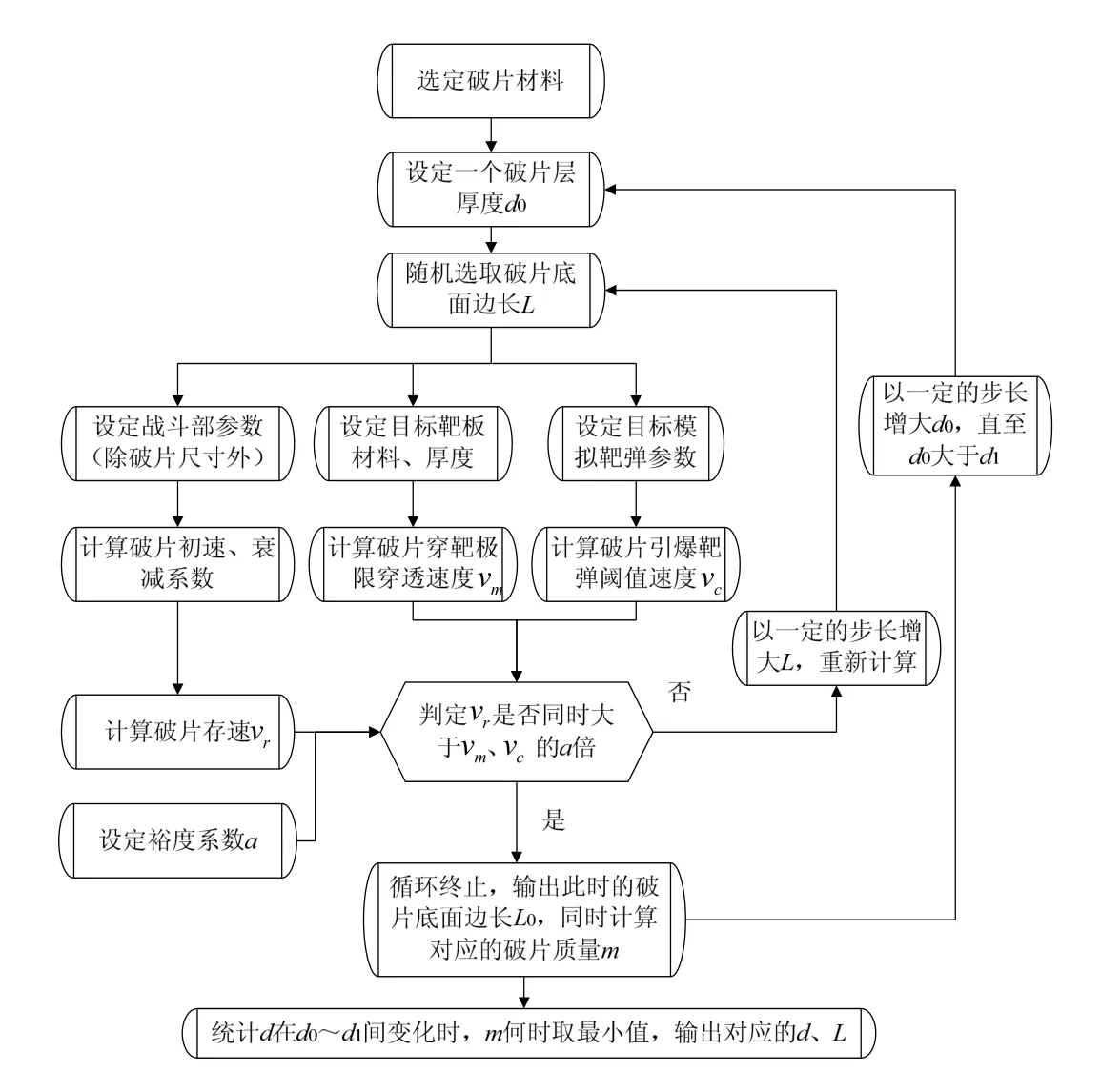
图5 破片层厚度在d0 ～ d1 间变化时，计算对应的反导破片最小质量流程

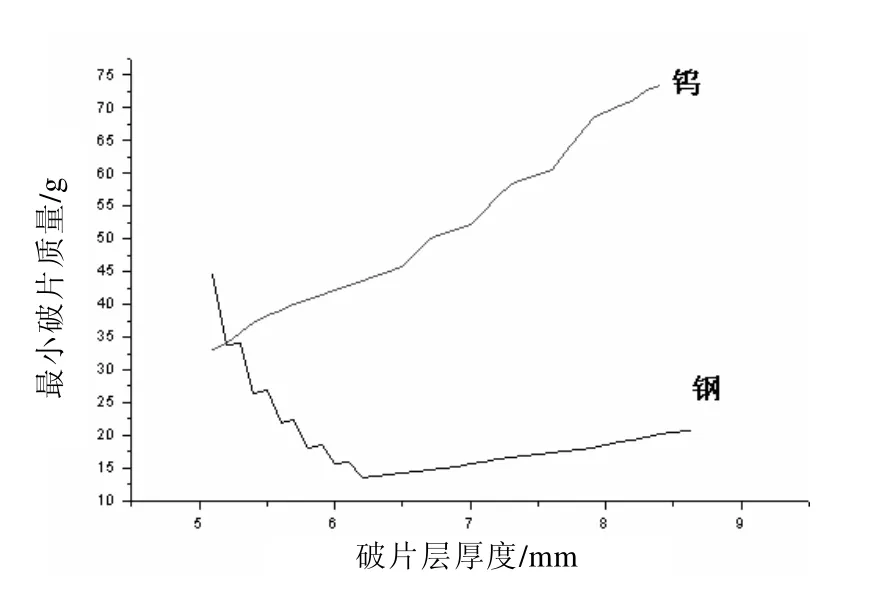
图6 破片层厚度变化时对应的最小破片质量

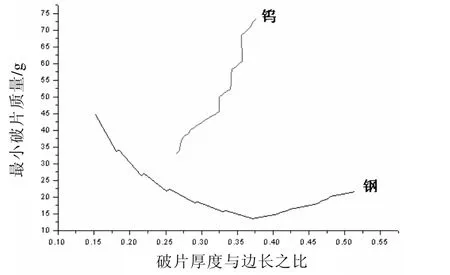
图7 λ 对应的最小破片质量

由图7可知，在该模型中，对钢破片，若λ=0.5，则破片质量最小值为20.9 g(8.7 mm×17.5 mm×17.5 mm)；对钨破片，λ 取值在0.265～0.376 间，且破片最小质量随λ 增大较快，钨破片显然不能满足使用要求。

3.2 战斗部重量、破片体对应装药长度的影响

在工程实践中，一般当战斗部重量、外形尺寸、基本结构确定后，分配给破片体对应部分的战斗部重量、破片体对应的装药长度是有限的。假设在表1的基础上，限定破片体对应部分的战斗部重量为24 kg，破片体对应的装药长度不大于280 mm，可得到破片层厚度与装药长度的对应关系见图8。

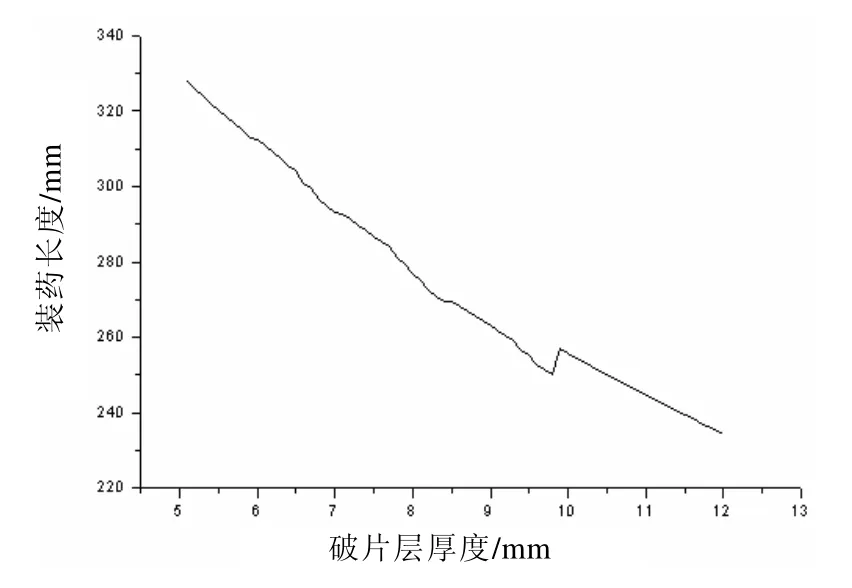
图8 装药长度与破片层厚度对应关系(对应部分的战斗部重量为24 kg)

由图8可知，当破片层厚度不小于7.9 mm时，装药长度才不大于280 mm。此时对应的反导破片优化设计结果为：7.9 mm×14.8 mm×14.8 mm 钢破片，单枚破片质量为13.58 g。

3.3 考虑动态交汇条件的影响

以上均是考虑静态条件下的优化计算，而实际的作战条件下，导弹与目标存在一定的交汇条件，使得破片与目标间还存在一定的相对速度，以及一定的入射角，破片动态飞散角示意图见图9，其中水平向右为导弹飞行方向[8]。

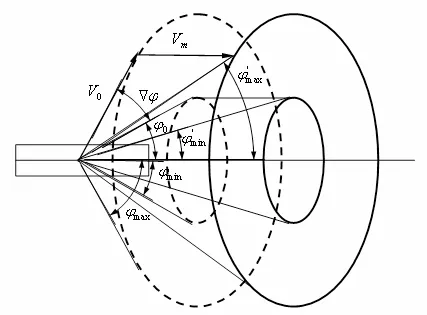
图9 破片动态飞散角示意图

图9中：ϕmax、ϕmin为战斗部静态破片飞散角的边界；ϕm′ax、ϕm′in为战斗部动态破片飞散角的边界。动态条件下的破片飞散方向角可按式(6)计算。

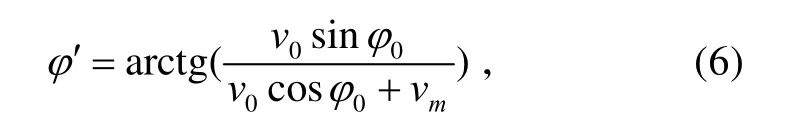
式中：ϕ′为动态条件下破片飞散方向角(°)；v0为破片静态条件下初速(m/s)；ϕ0为静态条件下破片飞散方向角(°)；vm为导弹末段速度(m/s)。

动态条件下叠加后的战斗部破片速度可按式(7)计算。

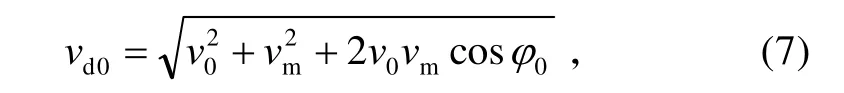
式中：vd0为破片动态合成速度(m/s)；v0为破片静态条件下初速(m/s)；ϕ0为静态条件下破片飞散方向角(°)；vm为导弹末段速度(m/s)。

根据以上两式，可计算出动态条件下的破片初速vd0，并根据动态条件下的破片飞散方向角ϕ′计算出动态条件下破片对目标的入射角度θ′，再按照前面的方法优化设计出战斗部动态条件下引爆给定目标靶弹需要的最小破片质量、对应的破片尺寸。

4 应用举例

根据3.2～3.3中介绍的计算方法，预设置一组参数利用VB 编程进行计算。

假设破片飞散方向角为104°～106°，导弹未段相对速度为1 300 m/s，以装药长度不大于280 mm、装药长度对应部分战斗部总重不大于24 kg、λ不小于0.5为约束条件。其余参数取值见表2，程序计算界面见图10。

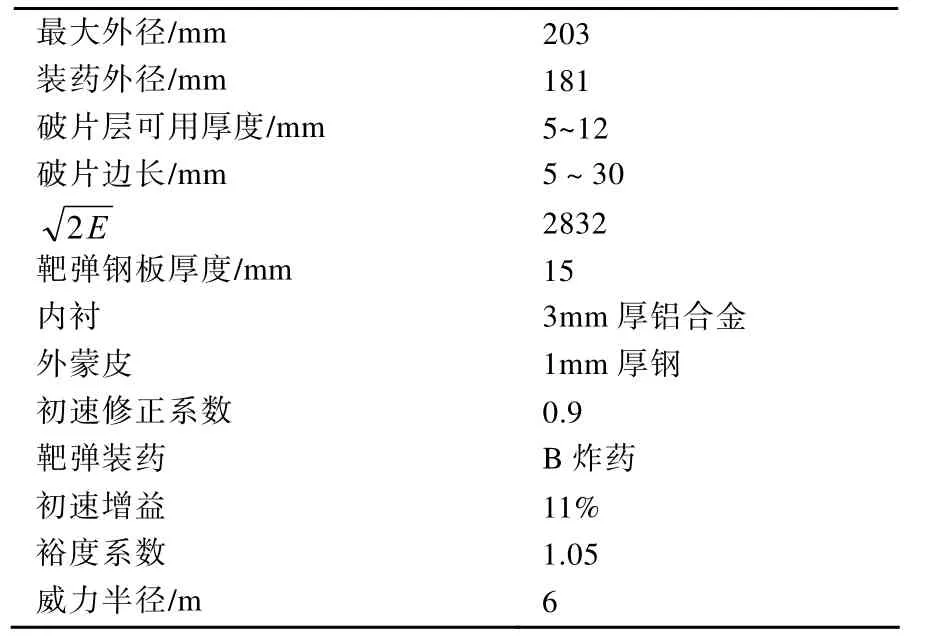
表2 其余参数取值表

图10 程序界面及参数取值

最终设计的破片参数见表3。表3中破片密度是按聚焦效率0.8 进行计算。

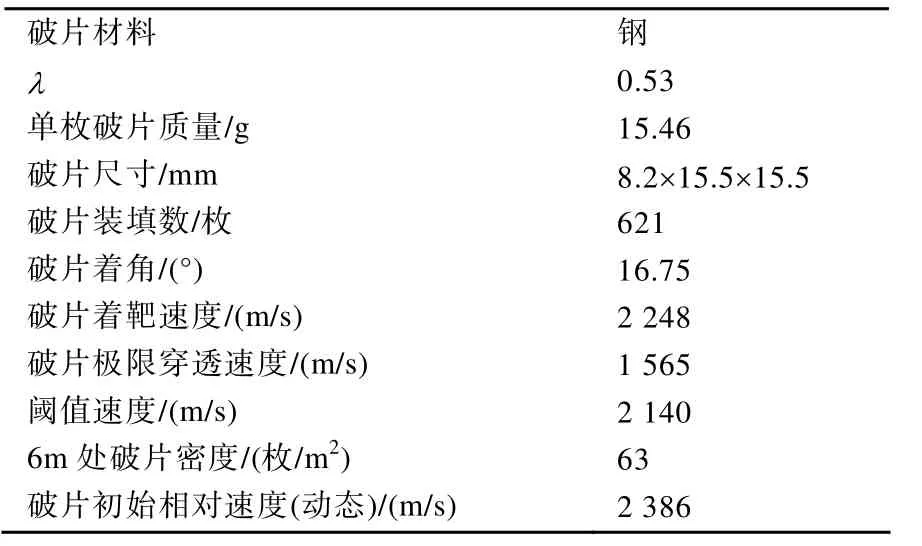
表3 最终设计的破片及相关参数值(威力半径6m)

5 总结

根据以上的分析计算，可以得出以下结论：

1)对单枚反导破片引爆给定厚度钢板屏蔽的炸药，在战斗部约束条件(外径、长度、重量)给定的条件下，对每种破片材料，均对应一个最小单枚破片质量，同时对应一定的破片尺寸；

2)同等约束条件下，采用钢破片可获得比钨破片更小的单枚破片质量，且采用钢破片的λ 更大，更不容易破碎；

3)实际应用过程中，应综合考虑破片的完整性、战斗部重量限制、装药长度限制、导弹交汇条件等因素进行二次筛选，才能确定最终的破片尺寸；

4)计算过程中存在多种修正系数，应结合工程实践经验选取，修正参数的选取对破片尺寸设计的最终绝对值影响较大，但不会影响优化计算过程中的基本规律。

[1]陈海利,蒋建伟,门建兵.破片对带铝壳炸药的冲击起爆数值模拟研究[J].高压物理学报,2006,20(1):109-112.

[2]王树山,李朝军,马晓飞.钨合金破片对屏蔽装药撞击起爆的实验研究[J].兵工学报,2001,22(2):189-191.

[3]梁争锋,袁宝慧.破片撞击起爆屏蔽B 炸药的数值模拟和实验[J].火炸药学报,2006,29(1):5-9.

[4]董小瑞,隋树元,马晓青.破片对屏蔽炸药的撞击起爆研究[J].弹箭与制导学报,1997,17(2):1-4.

[5]洪建华,陶江源.杀伤破片击穿和引爆靶弹的分析与研究[J].弹道学报,2002,14(4):60-66.

[6]隋树元,王树山.终点效应学[M].北京:国防工业出版社,2000:88-90,132-133.

[7]钱伟长.穿甲力学[M].北京:国防工业出版社,1984:220-221.

[8]李向东,唐晓斌,董平.破片式反导导弹引战配合仿真与效率计算[J].上海航天,2006(3):11-15.