声纳浮标阵目标搜索优化布放算法

匡贡献，谢志敏

（总参谋部气象水文局，北京 100081）

利用声纳浮标搜索潜艇是反潜战的一种重要形式，如何优化浮标阵的投放位置一直是研究热点。关于这方面的文献较多，主要有3大类：第1种是如何针对先验信息采用合适的阵形，文献[1]描述了方位线阵、垂直航向阵和圆形阵的使用方法，文献[1-2]讨论了拦截阵和包围阵在应召搜索中的使用时机；第2种是针对优化某一阵形参数从而达到提高搜索概率的目的，文献[3-5]讨论了螺旋线阵、方形阵和圆形阵的阵形参数对搜索概率的影响；第3种是权衡所有的阵形参数进行优化布放，文献[6-8]讨论了遗传算法在浮标优化布放中的应用，文献[9]利用Lipschitz Global Optimizer软件和模拟退火算法优化布放多基地声纳浮标。

浮标优化布放本质上属于箱约束的非线性全局优化理论研究范畴，解决这一类问题的方法较多。本文首先讨论了潜艇运动模型和搜索概率计算方法，然后提出了利用多点随机搜索算法、基于分区的分支界定算法和遗传算法优化布放浮标阵的方法，对比分析它们的优化效能。

1 问题描述

1.1 目的

在某海区Q 一批次投放n枚声纳浮标搜索单艘潜艇，搜索时间 t ∈[t1,t2]预先规定。假定浮标在搜索时间内一直能正常工作。优化布阵的目的就是利用n枚浮标在总的搜索时间内尽可能搜索到潜艇，衡量阵形好坏的指标是积累搜索概率(Cumulative Detection Probability，CDP)。

1.2 目标运动模型

应召搜潜通常通过其他途径得知某海域有潜艇活动信息，如红外设备观测到潜艇废气、海流特征等，但不知道潜艇的具体位置和运动状态。其初始位置散布特征和运动要素散布特征一般根据具体海洋环境、战场态势和量测信息进行设定。本文仿真假定目标初始位置服从圆正态分布，目标作匀速直线运动，航速在一定区间内均匀分布，航向在一定角度内均匀分布。

1.3 累积搜索概率计算方法

在实际过程中，由于海洋环境的复杂性，目标的初始散布特征和运动特征可能很复杂，加上浮标的漂移影响，使搜索概率计算不便于用某一解析式表达。因此，避开了复杂的数学推导，采用蒙特卡罗法(Monte-carlo，MC)计算搜索概率。

本文产生了3 000条MC目标轨迹，所有布放方案均针对这些轨迹运算，这样可以减少重复运算。对于被动声纳浮标，其作用距离还与目标的速度有关，速度越大其声源级越大，作用距离越大，反之亦反。为了加快运算速度，浮标作用距离计算往往根据各影响要素预先制表，以便在优化过程中不占用太多时间计算搜索概率，有关单双基地声纳的作用距离计算方法参考文献[10-12]。本文采用了一种简化检测准则，目标处于浮标有效探测半径r 内时，探测概率为1，否则为0。实际搜潜过程中，应当以浮标本身的ROC曲线为准。

2 浮标阵优化布放技术

浮标布放位置优化可以表示为

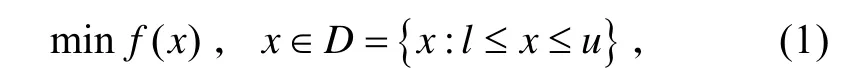
式中：f (x)为不被搜索到的概率；l、u分别为x的范围。

对于由单基地浮标组成的规则浮标阵，需要优化的变量较少，常用的均匀圆形包围阵只需要优化阵半径和阵心的位置，V形拦截阵需要优化顶点位置和V形张角；对于双/多基地浮标阵，不仅需要优化接收基站的阵形，而且还要对声源基站的位置进行优化，总体需要优化的变量较多。即使对于较少的变量，由于搜索空间大，不可能进行遍历搜索，需要利用合适的优化算法解决。目前最优化问题总体分为局部优化和全局优化。局部优化算法较多，如解非线性问题的最速下降法、拟牛顿法和可行方向法等。全局最优算法有遗传算法、蚁群算法、模拟退火算法、分支界定法、区间方法和填充函数等。

本文采用了3种全局优化算法优化浮标阵的布放位置，即多点随机搜索方法(Multi-start Random Search Algorithms，MS)、分区分支界定算法(branch-and-bound Based Partition Algorithms，BBP)和遗传算法(Genetic Algorithms，GA)。

2.1 多点随机搜索方法

该方法是一种简单的全局优化算法，不能保证找到全局最优点，表述如下。

Step1：设定停止准则(优化时间T 大于某值或连续M次优化值差别小于一给定足够小的正数ε 或循环次数大于某预设值N)，循环计数器i=0；

Step4：如满足停止条件取 Pi+1对应的终止；否则，i=i+1，转step3。

可见多点随机搜索方法能否找到全局最优主要取决于采样点的遍历性。另外，该方法具有并行特征，如果并行运算，大规模采样是可行的。

2.2 基于分区分支界定算法

以规则浮标阵的阵形参数作为自变量的不被搜索概率函数f是一种Lipschitz 连续函数，可以用BBP技术进行全局优化，并能保证找到全局最优解。区间技术主要用来计算目标函数的全局信息、函数界限和Lipschitz 常数，具体证明和性质可参考文献[13]。对于多维变量一般都采用分支界定策略以“剪除”明显不满足要求的区间。对于n个变量的范数算法描述如下。

Step1：设定停止准则(优化时间T 大于某值或f的上界与下界绝对值小于一给定的正数或循环次数大于某预设值N)，设定上界的初值为1，下界的初值为战术上允许目标不被搜索的概率的最大值。循环开始i=0。

Step2：在[l,u]上各区间上采样，利用采样值求Lipschitz 常数L 并更新上界，求第j 区间的弱化自变量及其弱化函数若说明该区间的最小值都大于规定的下界，可以“剪枝”，并将对于弱化自变量所在区间细分。对于二分法，一个分区裂成2n个小分区，i=i+1。

这种区间方法的优点是可以很容易求出各区间上的上下界并能保证找到最优点，缺点是运算速度慢，如果不能及早“剪枝”可能产生区间“爆炸”，因此说该方法只适合优化较少的变量。

2.3 遗传算法

遗传算法具有全局搜索能力，特别适用于多变量、多峰函数的最优化，关于基本遗传算法的实现原理可参考相关文献。整个过程表述如下。

Step1：设定停止准则(优化时间T 大于某值或进化代数大于某设定值)，循环计数器。

Step2：初始化种群，在[l,u]之间产生多个随机点 x0j(j=1,2,…,J)，并进行实数编码，取种群规模popsize=100。

Step3：进行选择、交叉和变异操作，交叉概率取0.6 变异概率取0.02。

Step4：如果满足停止条件，终止；否则，转step3。

3 仿真与分析

3.1 单基地声纳浮标阵优化布放的仿真

假定目标初始位置服从圆正态分布 N (0,σ2)，即

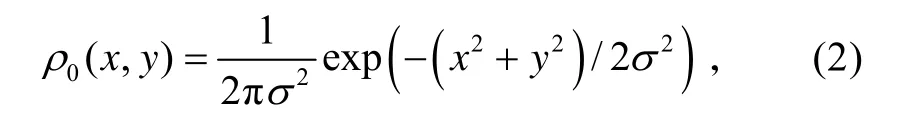
式中：x y、分别为横纵坐标；标准差σ=5n mile。目标作匀速直线方式运动，航速[5,15)节内服从均匀分布，航向在[5π/6,π/6)服从均匀分布，海洋环境各向同性。从基准时刻到开始搜索时延迟时间为1 h，搜索持续时间为1 h。这种已知敌潜艇航行扇面条件，采用拦截浮标阵较好，用文献[3]提供的算法布设3层拦截阵，共24枚浮标，每层均为8枚，拦截阵距基准点的距离分别为20、15和12 n mile。由于内圈的拦截阵主要针对低速目标，对应的目标辐射噪声小，相应被动声纳的作用距离也小，因此虽然内圈的跨度小，但还是布设相同的浮标数。对应极低航速的目标，如果再利用被动声纳浮标探测，其探测性能必然急剧减少，此时要实现无缝拦截需消耗大量的浮标，据此只布设了3 道拦截阵。

这种传统浮标布放方法能达到0.80的搜索概率，浮标布局如图1a)所示，能否有更好的布放算法提高搜索概率？以下内容利用多点随机搜索方法、分区分支界定算法和遗传算法进行优化布放，并与传统布放方法进行对比。设目标函数为式(1)表示的不被搜索到的概率，变量x为

x：[第1-3层拦截阵到基准点的距离，d1、d2、d3，对应各层的浮标数n1、n2、n3]

利用式(4)可将6个参数化为5个参数，采用上述3种方法进行优化。为了对比它们的性能，设置停止准则均为优化时间大于30 min。优化后的结果如图1b) ～ d)所示，MS、GA和BBP的CDP分别为0.82、0.85和0.90。虽然MS 布放方法的搜索概率超过了传统布放方法，但是与GA和BBP的优化结果相比，由于内圈浮标数量过多，致使实际搜索范围变小，因此在3种优化结果中其CDP是最小的。由于需要优化的参数只有5个，BBP 比GA 更能找到最优点，虽然两者优化的最终浮标布局相似，但BBP 具有更好的性能。

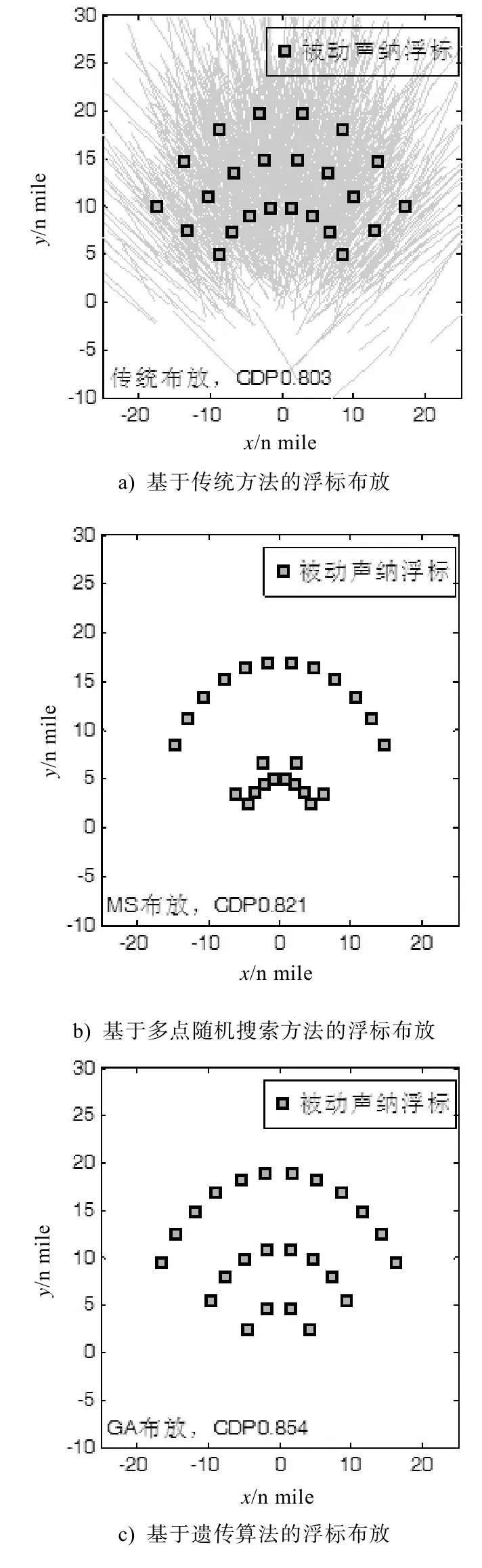
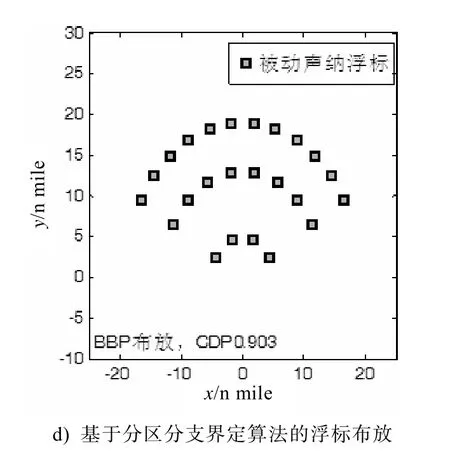
图14 种布放方法的被动声纳浮标布局及搜索概率对比，浮标数为24

3.2 双基地声纳浮标阵优化布放的仿真

假定目标初始位置特性和运动特性均与3.1仿真类似，目标初始位置误差标准差σ=2n mile，航速在[4,6]节内服从均匀分布。对于这种低速目标，被动声纳浮标的作用距离很小，必须采用主动探测，为了增强探测的隐蔽性，传感器采用双基地声纳浮标，其中发射基站1个，接收基站5个。虽然3.1仿真证明了MS、BBP和GA在被动浮标布放中有效，为进一步对比它们的性能，将其应用于双基地声纳浮标阵的优化布放。由于目前中文公开文献中没有关于双基地声纳浮标的传统布放方法，性能对比只限于3种优化方法之间，接收基站均采用了V形阵。

目标函数仍为式(1)中的不被搜索到的概率，变量x为

x：[V形顶点位置 xv、yv，V形的张开角θ，浮标的间隔d，发射基站位置 xs、ys]。

有6个需要优化的参数，设置停止准则均为优化时间大于30 min。进化后的结果如图2a)～c)所示，MS、GA和BBP的CDP分别为0.77、0.90和0.84。MS 由于遍历不够充分，性能最差，与仿真3.1相比多了1个参数，BBP的性能稍弱于GA。三者的进化曲线如图3所示，由图可知，虽然MS的最终性能差于其他两种方法，但在进化前期MS的结果是最好的，也就是说，如果要求运算时间短，采用MS 优化布放声纳浮标是可行的。

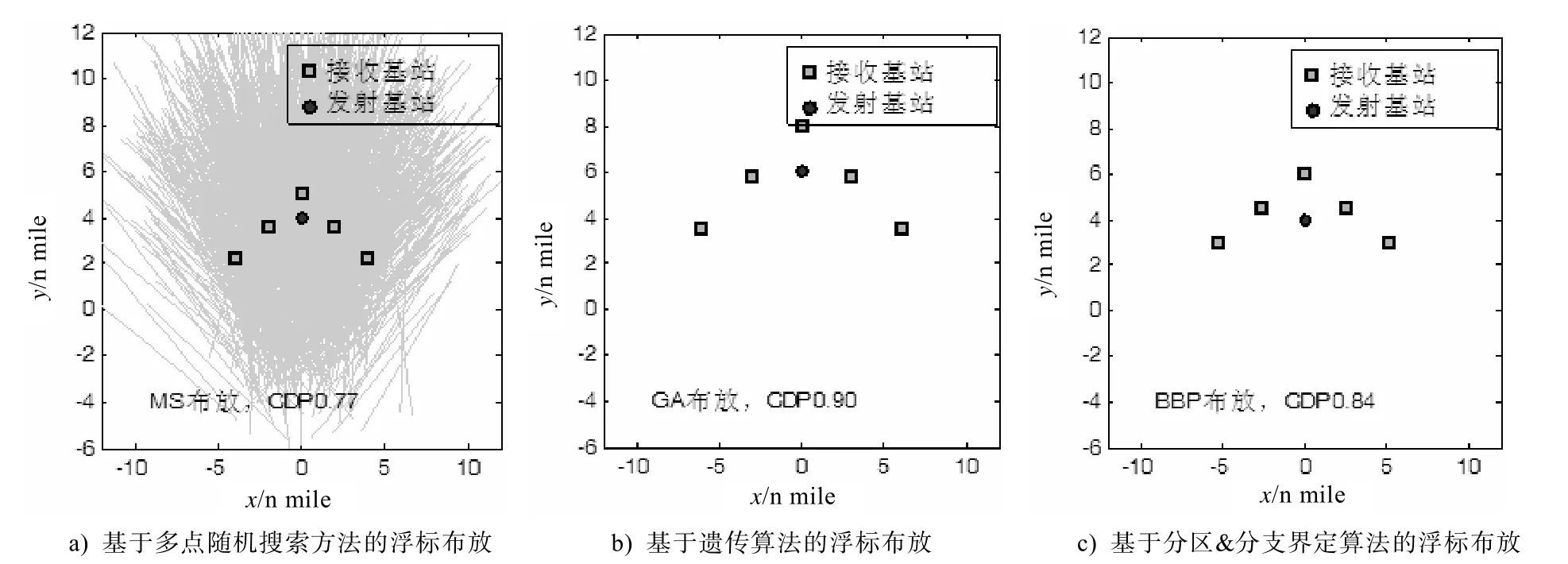
图2 双基地声纳浮标的优化布放，5个接收基站，1个发射基站

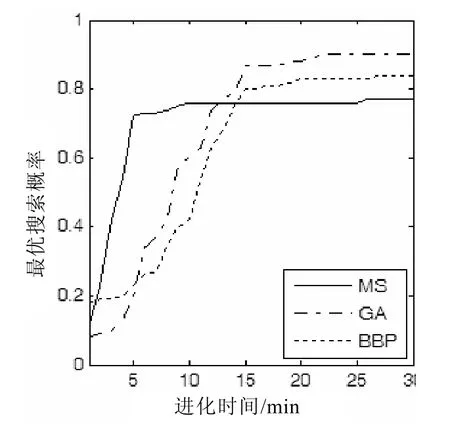
图3 MS、BBP和GA在双基地声纳浮标优化布放的进化曲线

4 总结

本文仿真比较了3种浮标优化布放方法，结果表明这3种方法相对于传统布放方法能提高搜索概率，对于相同的进化时间，多点随机搜索方法优化性能最差，但前期进化效果较好，适合短时间内制定浮标布放方案；分区分支界定算法保证能搜索到最优点，但优化参数不能太多；遗传算法较适合优化具有很多参数的复杂浮标阵，但是需要较长的进化时间。为了加快运算速度，下一步可以从两方面入手：一方面，在具有一定鲁棒性的前提下，通过调整遗传算子的相关参数加快运算速度；另一方面利用遗传算法的并行性。

本文介绍的方法与实际浮标搜潜过程相比，有一些因素没有考虑，如浮标漂移、投放时间、浮标可靠性等，在实际应用时，这些都是必须考虑的因素。另外就是没有在实际的复杂海洋环境下仿真。

[1]叶敬礼,罗德刚,宋裕农.舰载飞机使用声纳浮标搜潜阵式分析[J].火力与指挥控制,2002,27(增)∶53-55.

[2]丛红日.声纳浮标阵搜潜效能通用仿真模型研究[J].系统仿真技术,2010,6(2)∶104-106.

[3]杨日杰,王正红,周旭,张丹.浮标阵形对搜潜效能影响的研究[J].计算机仿真,2009,26(12)∶16-20.

[4]王磊,吴福初,陈钰宁,史海龙.基于声纳浮标的反潜直升机应召搜潜仿真研究[J].指挥控制与仿真,2010,32(2)∶84-88.

[5]丛红日,吴福初,王宗杰.圆形声纳浮标阵搜潜效能模型研究[J].海军航空工程学院学报,2010,25(1)∶93-96.

[6]周旭,杨日杰,高学强,韩建辉.基于遗传算法的被动浮标阵优化布放技术研究[J].电子与信息学报,，2008,30(10)∶2533-2536.

[7]墨岩峰,杨日杰,周旭.基于遗传算法的浮标优化布阵算法研究[J].微计算机信息,2010,26(7)∶208-210.

[8]墨岩峰,杨日杰,徐瑞来.遗传算法优化浮标布阵的可行性研究[J].国外电子测量技术,2010,29(1)∶23-27.

[9]GAMMON M A,SCHWARTZ B,PINTER J D.Enhancement of optimization capability in tactool using the lipschitz global optimizer (LGO) program[R].Defence R&D Canada-Atlantic,2007∶6- 12.

[10]杨日杰,何友,孙明太.主/被动联合多基地航空搜潜范围分析[J].航空学报,2004,25(4)∶381-384.

[11]杨日杰,何友,孙明太.航空搜潜装备搜潜范围建模与仿真研究[J].系统仿真学报,2003,15(11)∶1547-1550.

[12]凌青,杨丽,蔡志明.双(多)基地声纳浮标系统在反潜中的应用研究[J].海军工程大学学报,2006,18(2)∶47-49.

[13]PINTER J D.Global Optimization in Action[M].LONDON∶Kluwer academic publishers,1997∶91-108.