竖直环形流道内流动沸腾传热研究

孙立成，阎昌琪，曹夏昕

(哈尔滨工程大学 核能科学与技术学院，黑龙江 哈尔滨 150001)

在进行沸腾传热研究过程中，壁面的加热方式一般有电加热和流体加热2种方式.电加热方式采用电加热元件对壁面进行加热，可以等效成等热流的传热过程;流体加热是利用对流方式对壁面进行加热，既不能作为等热流方式来处理，也不能作为等壁温的传热过程.Darabi等［1］对这2种加热方法对传热特性的影响进行了评价，将不同学者得到的实验数据进行分析对比后得到:由于壁面上温度曲线不同是造成这种差异的主要原因.并阐明边界条件不同，传热特性也必然不同.

关于环形流道内沸腾传热过程、形成机理和计算模型方面，SU［2-3］等进行过较多研究.Hewitt［4］、Wolk［5］和Jayanti等［6］则对于流型的变化机理和判定方法进行了深入研究.本文针对水加热条件下的流动沸腾传热特性进行研究，并在可视化研究结果基础上，阐明传热机理，构建传热计算模型.

1 实验装置和实验参数

1.1 实验装置

实验装置系统如图1所示，整个实验装置主要由一回路系统和二回路系统组成.2组实验元件的结构如图2所示，主体由B30管和石英玻璃管同心套装构成，实验工质——水从下向上流经两管之间环形通道，并被内管反向流动的高温水加热.B30管的外径为16 mm，石英玻璃管的内径有22和26 mm两种，两组元件的流道宽度分别为3和5 mm.实验段的总长为1380 mm，有效换热长度为1350 mm.

一回路系统的工质采用去离子水.水在加热器内加热后，在水泵的驱动下流经实验元件的内管，同时和二回路水换热后，回到锅炉，完成一个循环.实验元件二回路入口处的预热器和一个自耦变压器相联，通过调整变压器功率，可以保证二回路入口温度为恒定值.二回路水首先经预热器预热，而后进入实验段，被加热到沸腾，最后在冷凝器冷却后回到二回路水箱.

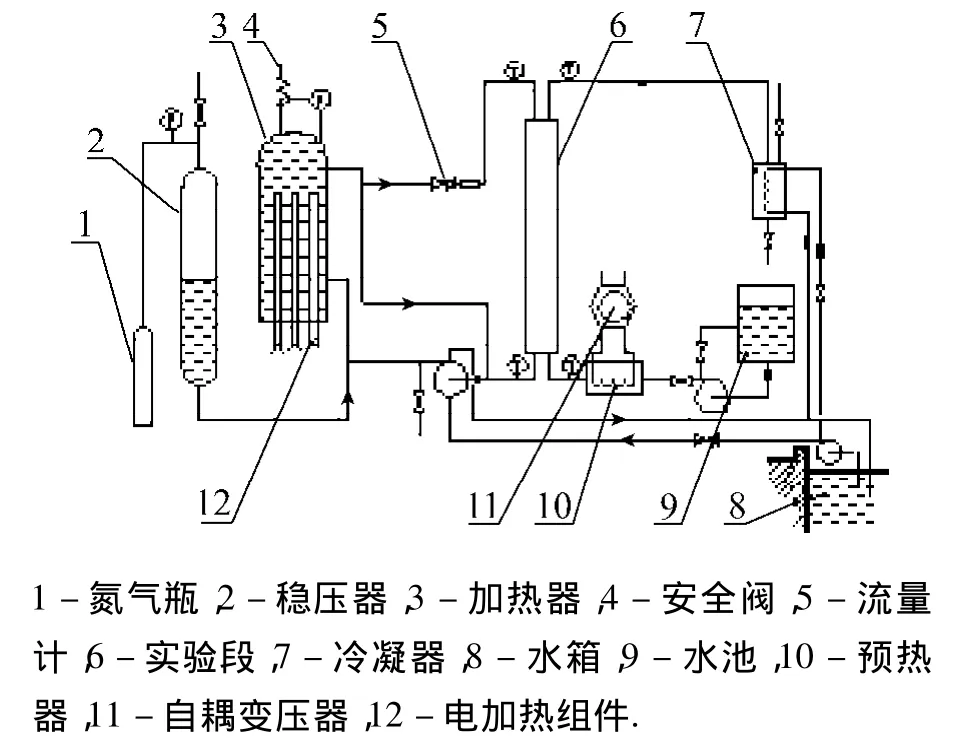
图1 实验装置Fig.1 Schematic of the test loop

1.2 实验参数

实验中具体的参数如下:

1)一回路

压力:0.8 MPa，

体积流量:0.74～1.41 m3/h，

水温:90～130℃.

2)二回路

压力:0.1 MPa，

质量流速:5 mm、16.8～55.3 kg/(m2s)，

3 mm、15.3～62.1 kg/(m2s)，

入口温度:40、50、60℃.

2 实验结果与分析

2.1 流型

2种环隙中出现的流型主要有泡状流、搅混流和搅混—环状流，如图3所示.泡状流一般发生在过冷沸腾区域，大部分气泡处在孤立状态，气泡之间互相干涉和聚合现象发生较少.在气泡聚集的位置，流型转变为搅混流，主流水温同时到达饱和点.搅混流是3种流型中最重要的流型，几乎占据了整个饱和沸腾区域.在实验段的上部，空泡份额较高，环状流和搅混流会同时发生，经常交织在一起，因此称之为搅混－环状流.

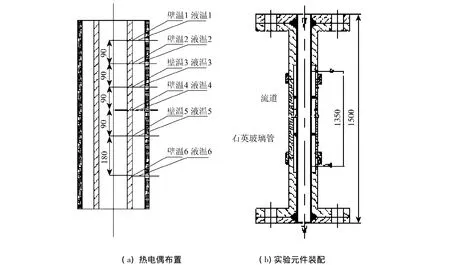
图2 实验元件Fig.2 Test section

需要指出的是，2种环隙在由泡状流向搅混流 过渡的位置呈现出一些不同之处.5 mm环隙，大量气泡在转变点聚集，并且聚集到一定程度才能发生流型的转变，因此壁面温度会出现一个小的峰值，一般在1～3℃范围内.3 mm环隙情况则不同，流型更容易从泡状流过渡到搅混流，气泡聚集后，流型立刻会发生转变，因此气泡的运动不易受阻，从而使得壁面的温度升高幅度很小.一般转变点的峰值不超过0.5℃.这一点可以从图4上看出来，图中的两条曲线分别是2种环隙内典型的壁温随热流的变化曲线.

图3 环隙内的流型Fig.3 Flow patterns in the annuli

2.2 影响传热的几个因素

图5反映的是质量流速对沸腾传热特性的影响，可以看出质量流速对饱和沸腾区域几乎没有影响，但对单相和过冷沸腾的传热却有很大的影响.这一点和电加热时的情况相似，提高流速，可以增强单相对流换热.

图6给出的是对应3个入口过冷度的沸腾传热特性曲线，入口过冷度分别为 60.38、50.28和40.89℃，入口过冷度为40.89℃时的传热强度低于另2种情况.增加过冷度虽然可以提高换热强度，但是并不是过冷度越高越好，入口过冷度为50.28℃时的传热特性略好于入口过冷度60.38℃时的情况.图7中除了3和5 mm环2条传热曲线外，还包含0.9、1.4和2.4 mm 3种环隙的传热曲线.其中2.4和3 mm环隙的传热特性要好于0.9和5 mm，可以看出适当的减少环隙宽度可以使传热增强，但是当环隙宽度过小时，使强化作用减小.

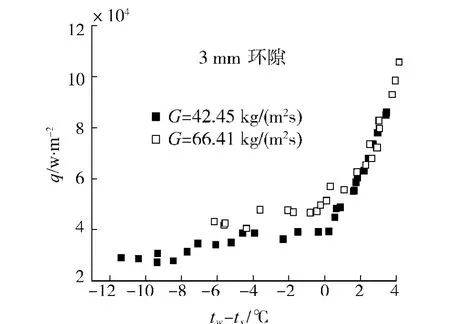
图5 质量流速对传热的影响Fig.5 Effect of mass flux on boiling heat transfer

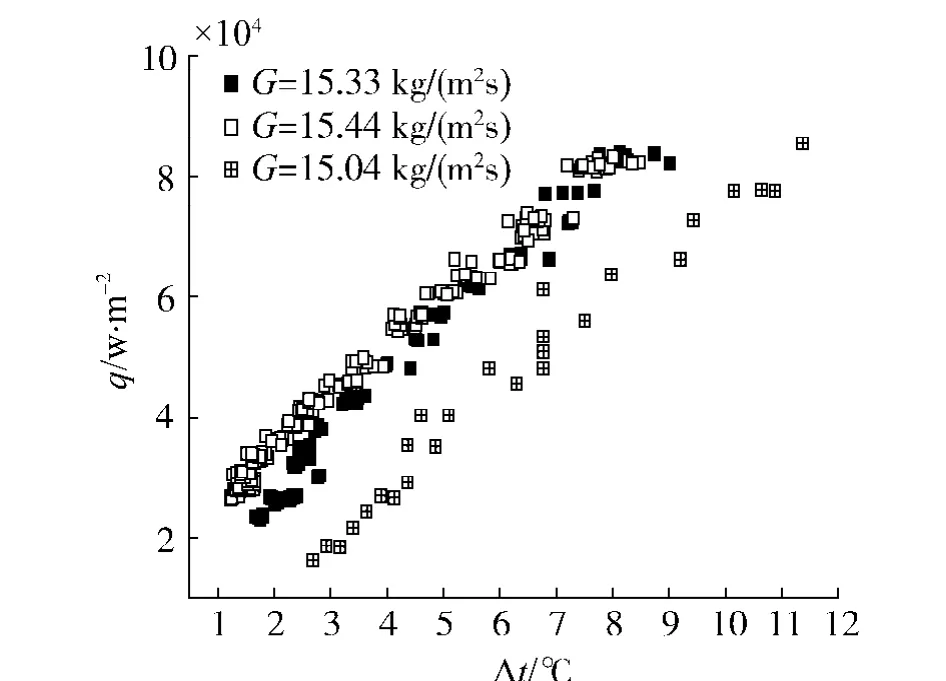
图6 入口过冷度对传热的影响Fig.6 Effect of subcooling on boiling heat transfer

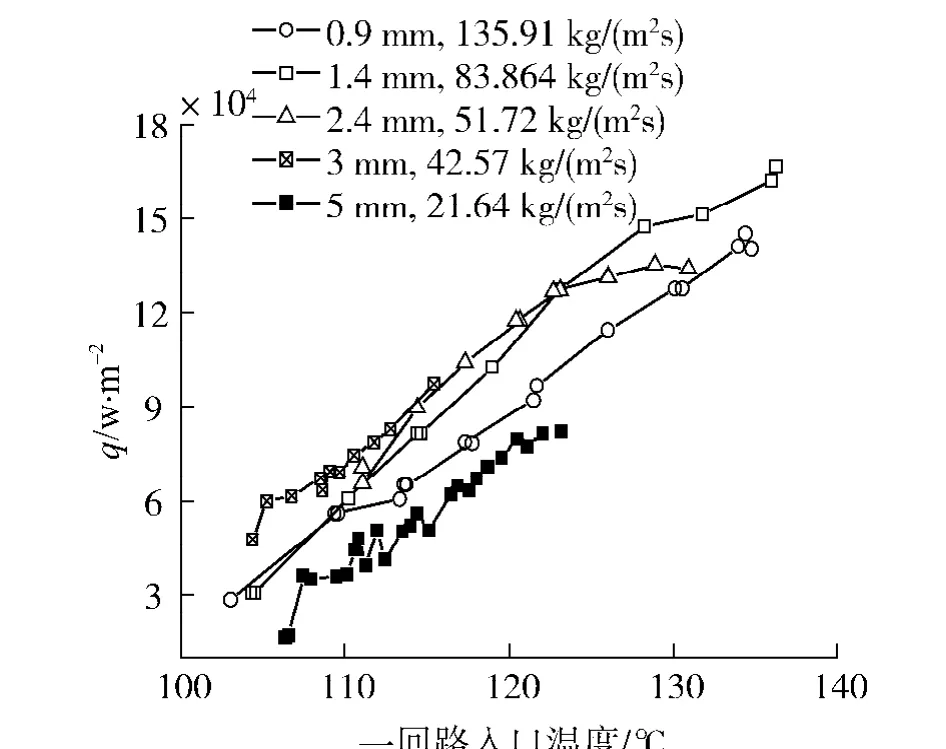
图7 环隙宽度对传热的影响Fig.7 Effect of annulus width on boiling heat transfer

3 传热模型

3.1 搅混流的形成机理

本文的可视化研究结果表明，搅混流是环隙内最主要的流型，几乎占据了整个饱和沸腾区域，因此建立传热模型前需要确定搅混流的形成机理.Hewitt等［4］的可视化研究结果表明:搅混流在本质上和环状流具有相似的本质，在流道中心有连续的气芯，在壁面上存在流动的液膜.Levy［7］将搅混流归结为环状流的一种;Wolk［5］和Jayanti等［6］根据液泛原理给出了比较准确描述从弹状流向搅混流过渡的判定公式.Su等［2-3］对于窄环形通道内的流动沸腾计算也是以环状流为基础.可以看出，一方面可以看出搅混流具有环状流的特点，另一方面液泛现象是其形成的机理.因此，本文的传热模型结合环状流模型、液泛原理和紊流理论建立.

稳流液膜的传热方程［8］可以写为

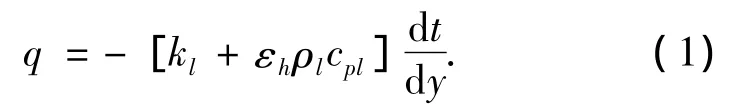
其中涡热扩散率εh可以由下面的公式计算［9］:

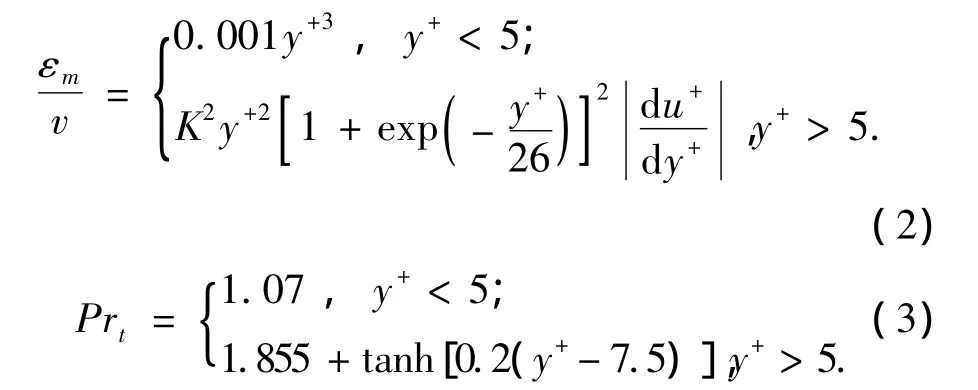
环状流液膜动量方程:

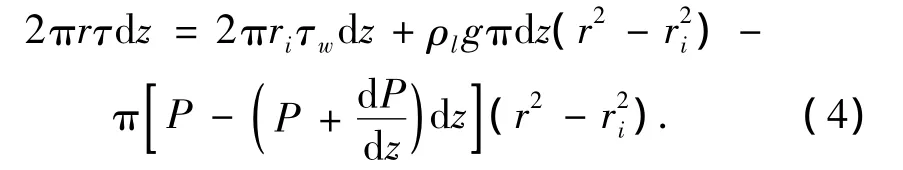
不考虑液体夹带的情况下，气相的动量方程:

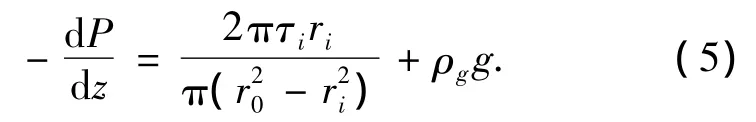
由式(4)得到液膜内某一位置的切应力为

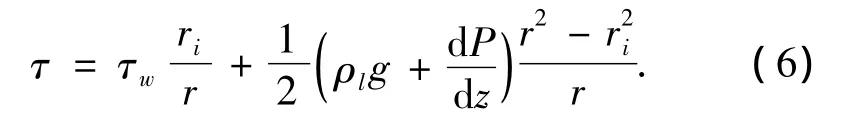
根据

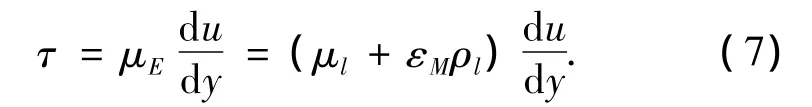
由式(6)和式(7)得到

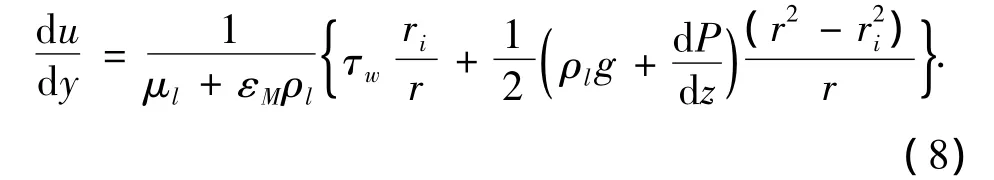
对于壁面切应力，Sawai等［10］根据液泛原理得到

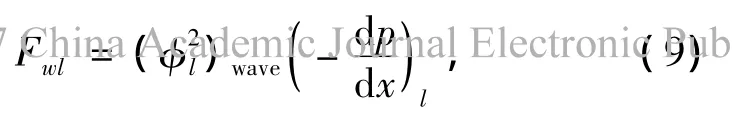
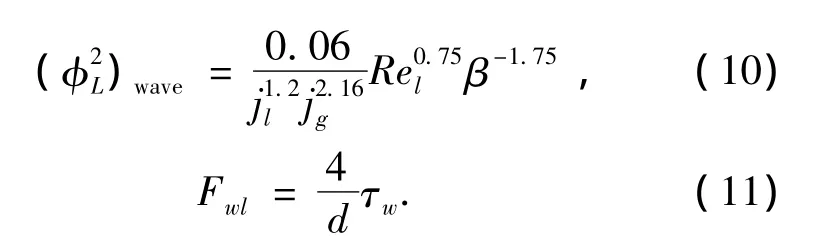
液体夹带率的计算:

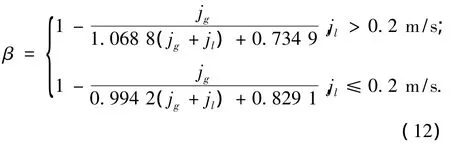
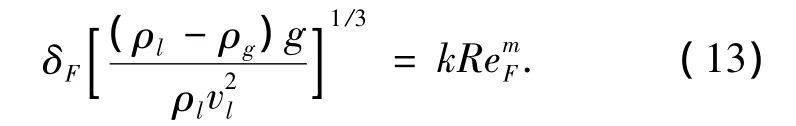
3.2 模型计算结果分析

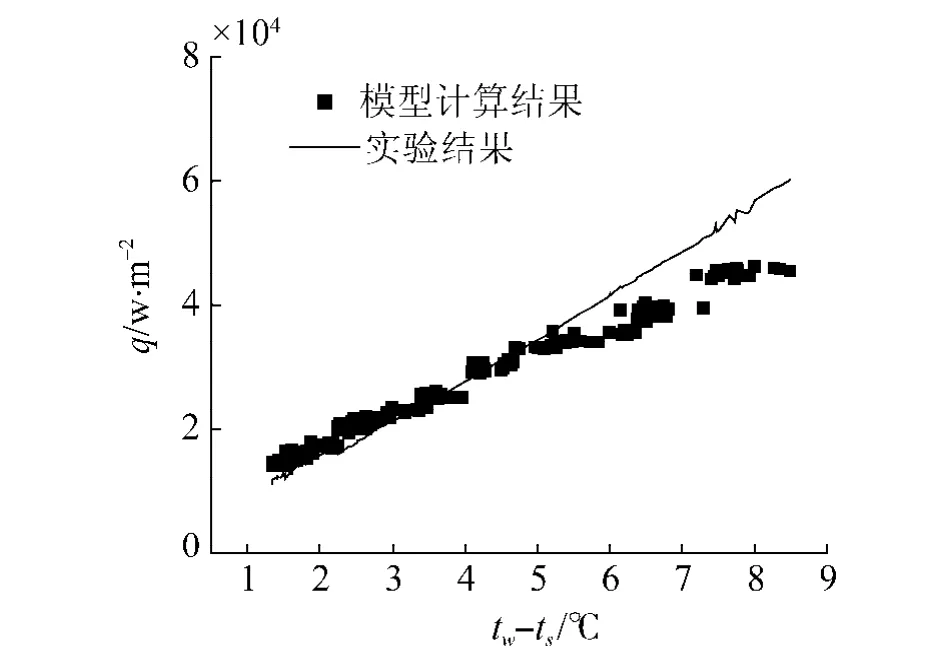
图8 5 mm流道实验结果和计算结果对比Fig.8 Comparison of 5 mm annulus between model results and experimental data

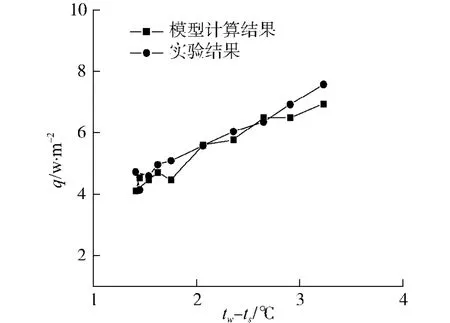
图9 3 mm流道实验结果和计算结果对比Fig.9 Comparison of 3 mm annulus between model results and experimental data

根据上节的模型，编制程序进行了求解.式(9)～(12)计算壁面切应力，式(11)计算液膜内的速度梯度，式(2)、(3)计算涡热扩散率.图8和图9分别是5 mm和3 mm环形流道的模型的计算结果和实验数据的对比情况，可以看出，5 mm流道的实验数据和模型计算结果之间相差几倍之多，但是在变化趋势上却非常相似;3 mm流道模型与计算结果之间相差更大.造成这些偏差的原因主要因为模型中壁面切应力和液膜厚度的计算公式都是从普通圆管中得到的经验公式，当用于尺度相对较小的环型流道时的适用性不好，另一方面搅混流本身是一个非常复杂的不稳定过程，对其发生机理的认识还需要进一步深入研究.

4 结束语

可视化研究表明:在3 mm和5 mm流道内的流型主要有泡状流、搅混流和搅混-环状流3种，而其中搅混流是最重要的一种流型，几乎占据了整个饱和沸腾区域;在流型从弹状流向搅混流转变时，3 mm流道内气泡运动不易受阻，更容易发生流型的转变，转变点位置的壁温峰值低于5mm流道;搅混流具有环状流的本质特征，其形成机理可以由液泛原理来解释，因此在传热模型中引入此模型，可以使模型更加合理.

附录

Cpl比热，J·kg－1·℃－1;u*摩擦速度，m·s－1;

tw壁温，℃; tb气泡周期，s;

tl水温，℃;

jg气相折算速度，m·s－1;

jl液相折算速度，m·s－1;

kl水的导热系数，W·m－1·℃－1;

FwL由壁面切应力导致的压降体度，Pa·m－1;

β液体夹带率; τ切应力Pa;

τw壁面切应力，Pa; ρl水密度，kg·m－3;

ρg气密度，kg·m－3; υ运动黏度，m2·s－1.

［1］DARABI J，OHADI M M，FANNI M A.Effect of heating boundary conditions on pool boiling experiments［J］.HVAC＆R Research，1999，5(4):1-14.

［2］SU G H，GOU J L，QIU S Z.Theoretical calculation of annular upward flow in a narrow annuli with bilateral heating［J］.Nuclear Engineering and Design，2003，225(2-3): 219-247.

［3］SU G H，GOU J L，FUKUDA K J.A theoretical model of annular upward flow in a vertical annulus gap［J］.J Nuclear Science and Technology，2003，40(1):1-11.

［4］HEWITT G F，MARTIN C J，WILKES N S.Experimental and modeling studies of annular flow in the region between flow reversal and the pressure drop minimum［J］.PCH Phisicochem Hydrodyn，1985，6:69-86.

［5］WOLK J，DREYER M，RATH H J.Flow patterns in small diameter vertical non-circular channels［J］.International Journal of Multiphase Flow，2000，26(6):1037-1061.

［6］JAYANTI S，HEWITT G F.Prediction of the slug-to-churn flow transition in vertical two-phase flow［J］.International Journal of Multiphase Flow，1992，18:847-860.

［7］SALOMON L.Two-phase flow in complex systems［M］.New York:John Wiley＆Sons Inc，1999:221-222.

［8］BUTTERWORTH D，HEWITT G F.Two-phase flow and heat transfer［M］.2nd ed.Oxford:Oxford University Press，1978:179-180.

［9］WILLIAM M K.Turbulent Prandtl number-Where are we［J］.Journal of Heat Transfer，1994，116:284-295.

［10］SAWAI T，KAJI M，KASUGAI T，NAKASHIMA H，MORI T.Gas-liquid interfacial structure and pressure drop characteristics of churn flow［J］.Experimental Thermal and Fluid Science，2004，28(6):597-606.

［11］CHEN X T，BRILL J P.Slug to churn flow transition in vertical two-phase flow［J］.Chemical Engineering Science，1997，52:4269-4272.