经验贝叶斯岭估计在加速度计标定中的应用

姜岩松，刘雨，苏宝库

(哈尔滨工业大学 空间控制与惯性技术研究中心，黑龙江 哈尔滨 150001)

在惯性导航系统中，加速度计的精度直接影响导航和制导系统的精度［1］.通过改进测试技术和辨识方法来提高加速度计精度成为惯导领域重要的科研目标.在加速度计重力场标定试验中，由于测试设备存在转角误差，结果并不理想.考虑到正交双表g2观测模型可以消除设备转角误差的影响［2］，但同时模型的系统矩阵中由于某些误差项线性相关，使得在计算出现不满秩，造成系统存在较为严重的复共线性.若用传统的最小二乘方法会出现估计偏差过大、对样本变化敏感、分离不出耦合在一起的误差项［3］.对于上述存在问题，本文首先给出正交双表g2观测模型，分析了复共线性产生的原因，而后融合了贝叶斯估计和岭估计的思想，即从历史数据中估计出先验信息计算出验后概率，然后以某种准则求出岭参数［4-5］，最后将岭参数代入估计量中进行统计推断和决策［6-7］，提出了经验贝叶斯岭估计法，并推导了具体的求解过程.最后通过仿真分析和加速度计在重力场的实测试验数据，比较了最小二乘法和经验贝叶斯岭估计法.

1 加速度计正交双表误差模型

在分度头上进行多位置翻滚实验可以对加速度计标定.当绕PA轴旋转时，假设水平位置为初始位置(A表的IA轴指向西)，转角θ顺时针旋转为正.设两块加速度计在分度头上的安装取向是几乎正交的，得到A表的模型方程:

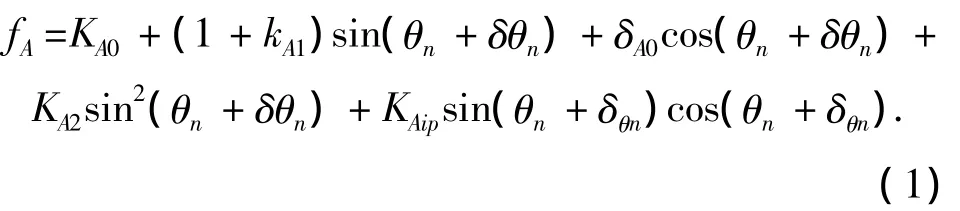
B表转动η+90°时的模型方程:

式中:δθn是加速度计在转角θn位置时的转角误差(n=1，2，…，N是角位置数)，η为两表的非正交误差.

设全部模型系数的平方与乘积都可以忽略，得到g2观测模型方程为

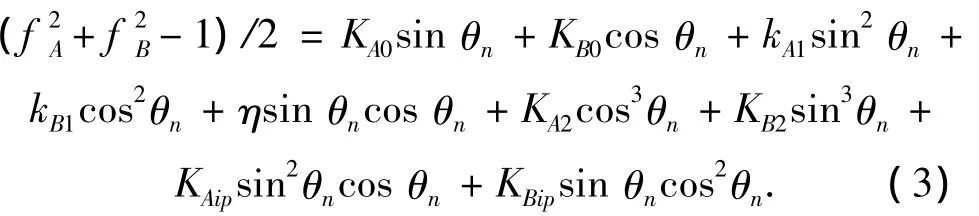
式(3)的正交双表模型的矩阵形式为

其中:Y=［y1y2… yn］T是观测值;ε=［ε1ε2… εn］T，εn是假设在θn位置时的测量噪声; K=［KA0KB0kA1kB1η KA2KB2KAipKBip］T是被估计参数;A为系数矩阵由式(3)给出.

被测加速度计的精度高于转角精度时，采用正交双表法可以有效消除转角误差对测试的影响.将式(3)化为三角函数的标准形式:

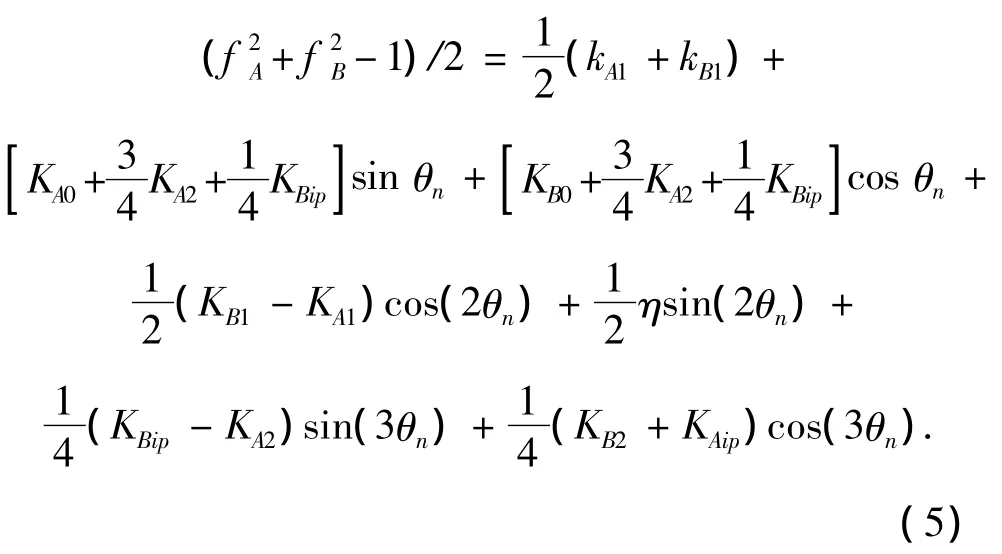
由式(5)可以看出A表的KA0、KA2和B表的KBip耦合在一起，B表的KB0、KB2和A表的KAip耦合在一起，存在线性相关，导致这些参数在一次实验中无法完全分离出来.

2 经验贝叶斯岭估计

2.1 问题描述

不失一般性，对于形如式(4)的线性回归模型:

式中:Y=［y1y2… yN］T;β=［β1β2… βm］T; A是N×m的系数矩阵;ε=［ε1ε2… εN］T是独立同分布且服从N(0，σIN).为获得β的minimax估计，考虑损失函数:

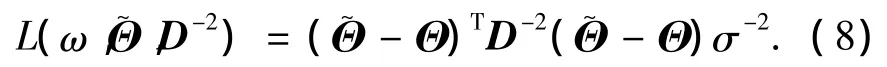
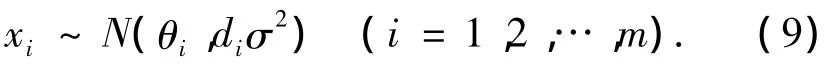
式中:di是已知的，σ2是未知的可以通过下式估计出:

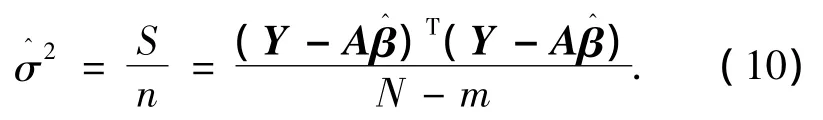
因此问题就转化为通过xi来估计θi.

2.2 经验贝叶斯岭估计的算法

对于式(9)，假设θi先验分布为N(0，λσ2)，xi的条件密度函数为

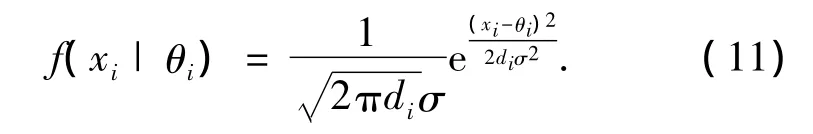
θi的先验密度函数为

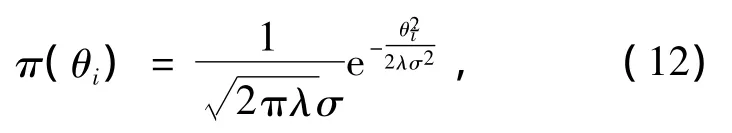
则θi的验后密度函数为

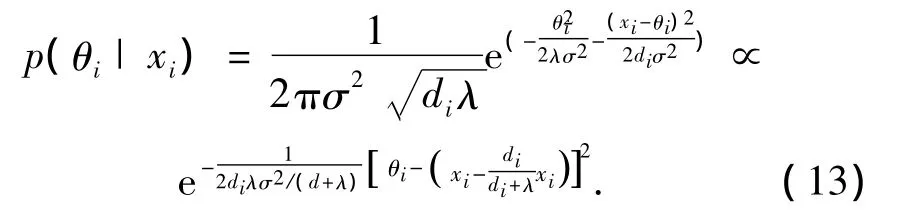
式(13)表明若xi是给定的，那么θi的验后分布为得到θi的贝叶斯估计:

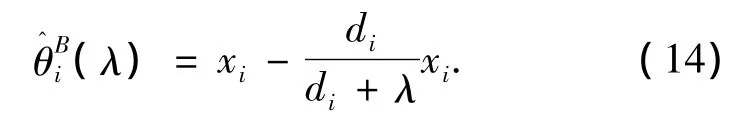
文献［8］给出了一个关于求λ估值的方程:

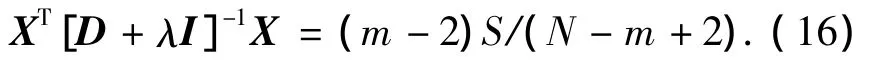
展开将S移到等式左面并令λ*为以下方程的解:

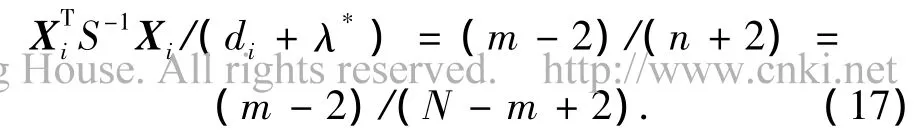
同时令λ0为以下方程的根:

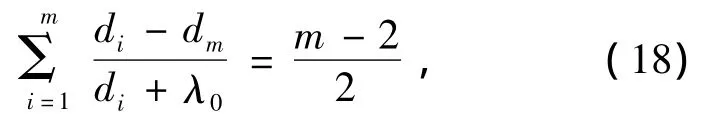
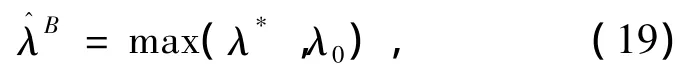
将式(19)代入式(14)可得到θ2的估计:

3 仿真与实验验证

3.1 仿真分析

为了检验经验贝叶斯岭估计的有效性，首先进行了最小二乘估计(LS)和经验贝叶斯岭估计(EBR)的仿真研究.对于式(6)的辨识模型，取以下待辨识参数:零偏K0、一次项修正值k1、交叉耦合项Kip、二次项K2、安装误差角δθ和非正交误差项η，用R表示拟合残差.可按照式(15)中和式(20)计算出单表最小二乘、双表最小二乘及双表经验贝叶斯岭估计的估值与估值标准偏差.

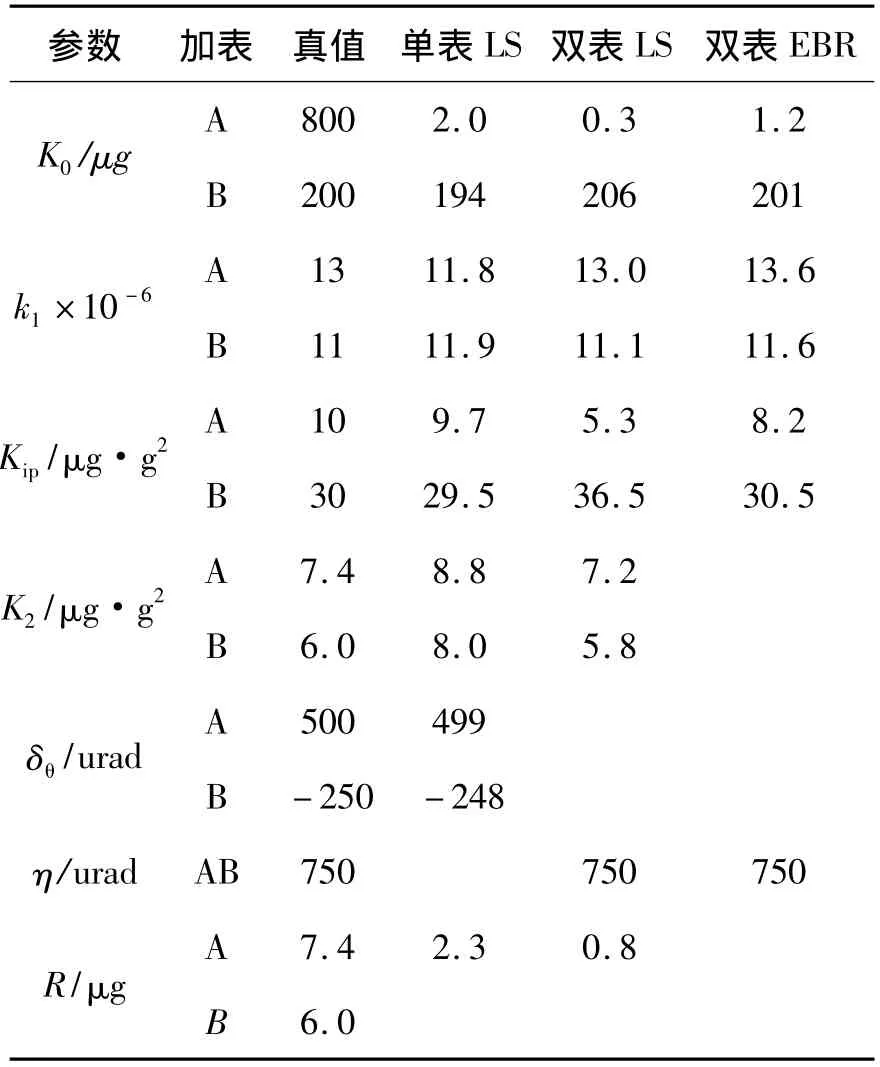
表1 最小二乘估计(LS)和经验贝叶斯岭估计(EBR)估值仿真结果Table 1 The simulation result of estimate by LS and EBR

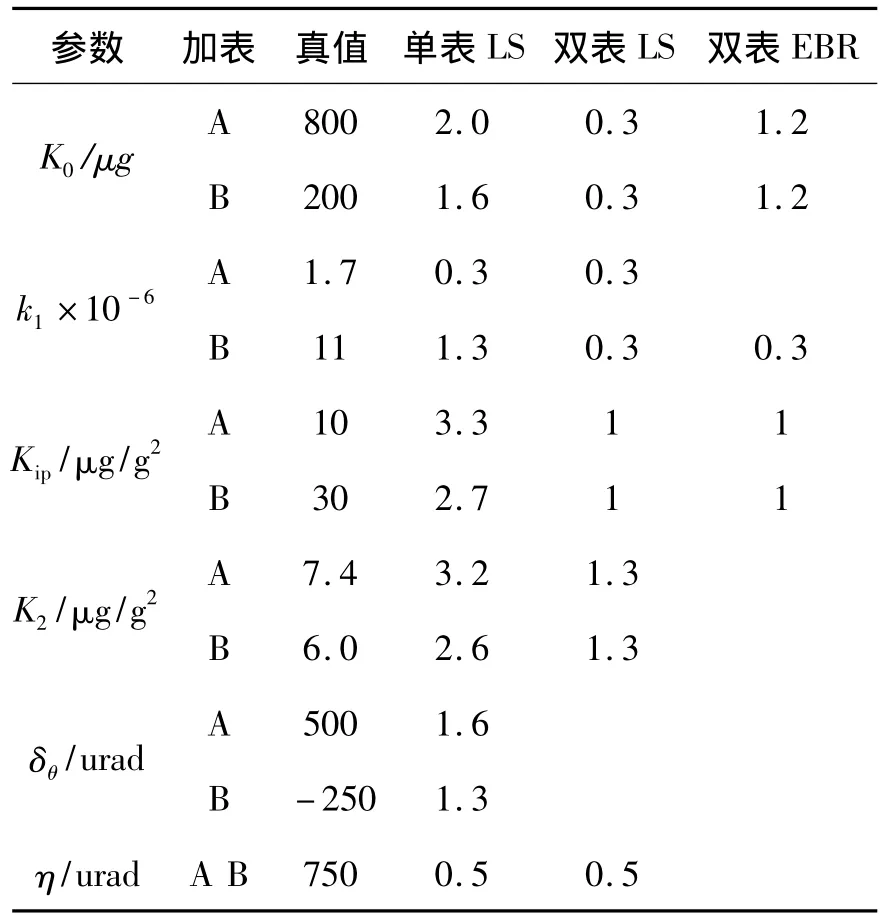
表2 最小二乘估计(LS)和经验贝叶斯岭估计(EBR)估值标准偏差仿真结果Table 2 The simulation result of standard deviation by LS and EBR

分析表1和表2仿真结果，比较3种方法的拟合残差R可知，利用单表最小二乘估计其拟合残差R较大，辨识精度低;双表最小二乘无法同时分离Kip和K2;双表经验贝叶斯岭估计不但拟合残差较双表最小二乘估计小、辨识精度高，而且能够估计出二次项K2，进一步说明了经验贝叶斯岭估计在加速度计双表模型参数辨识中的优越性.

3.2 实验验证

高精度加速度计的测试对实验设备及实验环境有很高的要求.

3.2.1 实验设备及实验环境

实验中所用到的仪器、测试设备及实验环境说明如下:

1)通常加速度计的重力场实验是利用精密分度头或精密转台来实现的，本实验所用到的是上海理工大学附属工厂生产的SJJF－1型1角秒精密光学光栅分度头;

2)两块加速度计是某研究所研制的石英挠性加速度计，其精度约为1×10－5g;

3)电压表为KEITHLEY2000六位半数字多用表;

4)实验室地基(见图1);

5)测试温度变化不超过0.2℃，温控装置见图2;

6)低温恒温装置(图3)控制高精密(10－6)采样电阻的温度;

7)实验时间选为室外环境安静的傍晚.

图1 实验室隔振礅Fig.1 The foundation

图2 温控装置Fig.2 The temperature control device

图3 低温恒温槽Fig.3 The low and constant temperature device

3.2.2 实验步骤

加速度计的初始安装位置为门状态，即绕摆轴PA进行多位置翻滚实验，如图1所示.初始安装完成应进行调平，使得加速度计A的输入轴接近于水平位置.通过对实验位置数和实验点选取的D最优分析，认为等角间隔20位置取点是最优的.

实验开始时，分度头示数为0°，待数字万用表稳定后，记录两块加速度计的电压输出值，然后逆时针依次转动到18°、36°、54°、…、360°(20位置)，在每个转角位置分别记录精密分度头的转角和两块加速度计的输出数据，最后再按照上述方法完成一次顺时针测量，将两次实验结果各个位置的读书取平均后作为一次实验数据.

图4 正交双表安装方式示意图Fig.4 Installation diagram of two orthometric accelerometers

3.2.3 结果分析

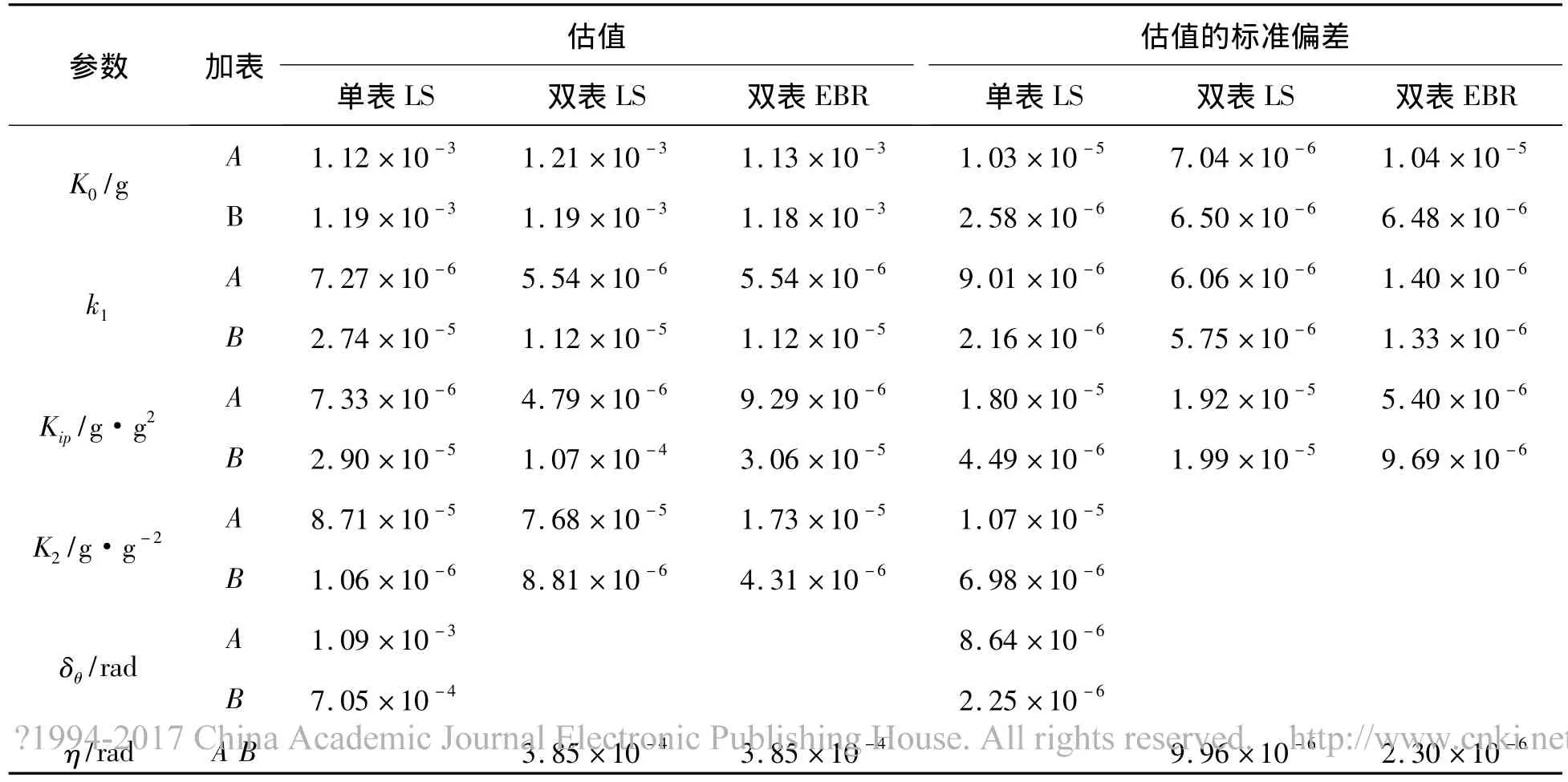
表3 最小二乘和经验贝叶斯岭估计的实验结果Table 3 The result of the experiment by LS and EBR

从表3实验结果分析可知，应用最小二乘和经验贝叶斯岭估计其零次项、一次项修正值及非正交项的估计结果基本一致.双表的最小二乘估计可以消除安装误差角的影响，但二次项和耦合项的线性相关问题得不到解决;单表模型虽然每个参数都能辨识，但由于安装误差的引入，使辨识精度降低.双表的经验贝叶斯岭估计解决了上述问题，在保证辨识精度的同时还估计出了K2.

对于K2项辨识结果，参照加速度计出厂时的产品检验合格证书中的 K2项标称范围，即:KA2＜9.4×10－5g/g2，KB2＜2.5×10－5g/g2，估值均在参考范围内，可认为辨识结果是真实可信的.

4 结束语

为提高加速度计的精度，基于加速度计的正交双表模型，本文提出了一种经验贝叶斯岭估计方法，从仿真和具体实验两方面，对比了单表的最小二乘估计、双表的最小二乘估计和经验贝叶斯岭估计的精度.结果证明，在正交双表g2观测模型中应用经验贝叶斯岭估计能够克服系统的复共线性问题，并且辨识精度好于最小二乘法，对于解决由于模型相关项导致无法用最小二乘法辨识这类问题非常有效.此外，加速度计的高次项，如:K2和K3等系数的标定对测试设备和测试环境要求很高，试验非常昂贵，在文中阐述的加速度计试验，经验贝叶斯岭估计方法利用历史的有效数据分离出二次项，对高精度加速度计的测试有很大的理论价值和工程实用价值.对于三次项、高阶非线性项和交叉耦合项是否依然满足适用条件，需要结合离心机试验进一步研究.

［1］张春京，原俊安，李丹东.从加速度计测试技术研究看惯性仪表测试技术发展趋势［J］.航天控制，2005，23 (2):78-84.

ZHANG Chunjing，YUAN Junan，LI Dandong.Inertial device test technology in view of the study of accelerometer test［J］.Aerospace Control，2005，23(2):78-84.

［2］Gyro and Accelerometer Panel of the IEEE Aerospace and Electronic System Society.IEEE Std 1293-1998.IEEE Standard Specification Format Guide and Test Procedure for Linear，Single-Axis，Nongyroscopic Accelerometers［S］.New York:The Institute of Electrical and Electronics Engineers，1998:187-208.

［3］Gyro and Accelerometer Panel of the IEEE Aerospace and Electronic System Society.IEEE Std 836-2001.IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers［S］.New York:The Institute of Electrical and Electronics Engineers，2001，11:12-25.

［4］陈希孺.数理统计引论［M］.北京:科学出版社，1981: 439-528.

［5］KUBOKAWA T，SRIVASTAVA M S.Minimax multivaricate empirical Bayes estimators under multicollinearity［J］.Journal of Multivariate Analysis，2005，93:394-416.

［6］STIRLING W C，LEE S A.Decision-directed multivariate empirical bayes classification with nonstationary priors［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence 1987，9(5):644-660.

［7］KUBOKAWA T，SRIVASTAVA M S.Improved empirical Bayes ridge regression estimators under multicollinearity［J］.Communications in Statistics:Theory and Methods，2004，33(8):1943-1973.

［8］SHINOZAKI N，CHANG Yuantsung.Minimaxity of empirical Bayes estimator of the means of independent normal variables with unequal variances［J］.Communications in Statistics:Theory and Methods，1993，23(8):2147-2169.