一类含强迫项的二阶微分方程解的振动性

陈慧琴

(山西大同大学数学与计算机科学学院,山西大同037009)

振动理论是微分方程定性理论的一个重要分支,在科学技术领域中有着广泛的应用。近几十年来取得了很大的发展,并有大量的研究成果和专著发表[1－6]。文献[1]中已经讨论了含强迫项的二阶线性微分方程

解的振动性，本文对其振动性又给出一个补充定理，介绍由强迫项f（t）引起的振动问题。其中方程(1)对应的齐次方程为

方程(1)、(2)中的 p（t）及 x（t）都是[a,+∞)t a≥0上的连续函数。为了得到(1)振动的定理，先给出

引理 1 如果 φ（t）是方程(2)解，x（t）是(1)的解，令 x（t）=φ（t）y（t），则 y（t）满足方程

证明 把 x（t）=φ（t）y（t）代入方程(1)中，得

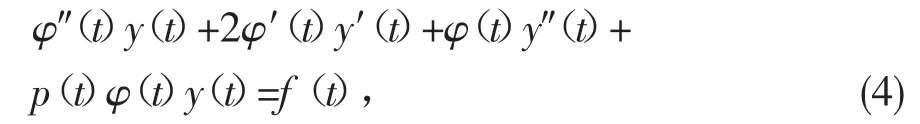
(4)式两边同乘以 φ（t），则

由于 φ（t）是方程(2)的解，所以(3)成立。

定理2若存在方程(2)的一个正解φ（t），对于一个正实数T,使得

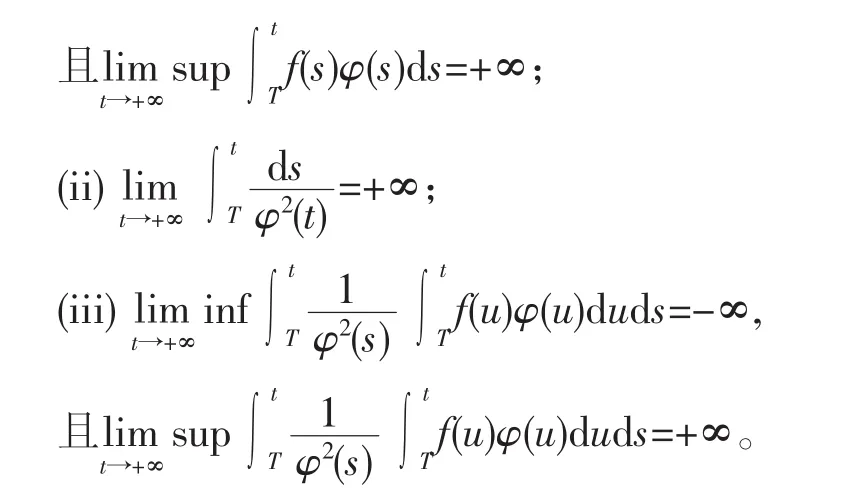
那么方程(1)是振动的。

证明假设方程(1)有一个非振动解x（t）,即存在t1＞0，当 t≥t1＞0 时，x（t）＞0。

令 x（t）=φ（t）·y（t）

则由引理知 y（t）满足方程(3)，对(3)由 T 到 t积分，得

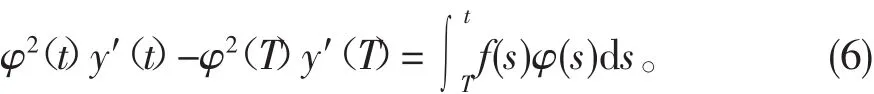
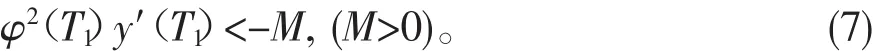
由(6)得

对(8)从T1到t积分，得

由条件(iii)及(9)，知存在 ti，使得 y(ti)＜0，这与y(t)＞0矛盾。当x(t)＜0时，类似可证结论成立，问题得证。

例二阶微分方程

对应的齐次方程为

方程(11)存在一个正解φ(t)=e-t，满足定理2的条件，则由定理2知，(10)有振动解，实际上方程(10)的振动解为

关于方程(1)的振动性，读者可参阅文献[1]，本文中只是给出了方程(1)振动的一个补充定理，此定理的条件比文献[1]中定理3．1,3．2的条件更强，但应用本文定理判别方程(1)的振动性更为方便。

[1]燕居让．常微分方程振动理论[M]．太原:山西教育出版社,1992．

[2]Gyori I,Ladas G．Oscillation Theory of Delay Differential Equations with Applications[M]．Oxford:Clarendon Press,1991．

[3]Erbe L H,Qingkai Kong,Zhang B G．Oscillation Theory for Functional Differential Equations[M]．Hong Kong:Marcel Dekker,1995．

[4]Chen Huiqin,Jin Zhen．Oscillation Criteria of Solution for a Second Order Difference Equation with Forced Term[J]．Discrete Dynamics in Nature and Society,2010：1－6,ID 171234．

[5]Chen Huiqin,d Jin Zhen．Monotonicity of eventually positive solutions for a second order nonlinear difference equation[J]．International Conference on Computational Aspects of Social Networks,2010:189－191．

[6]陈慧琴，赵香兰．一类二阶微分方程最终正解的单调性[J]．山西大同大学学报:自然科学版,2010,26(5):3－4．