方势阱中的束缚态
张子珍,杨成全,康占成
(山西大同大学物理与电子科学学院,山西大同 037009)
1905年,A.Einstein用Plank的量子假设去解决光电效应问题时,提出了光量子的概念。De Broglie仔细分析了光的微粒说及波动说发展的历史,提出了物质波的假说。1926年,Born把微观粒子的波动性与粒子性统一起来,提出的几率波概念。1927年,Heisenberg提出测不准关系,将经典粒子的概念对微观世界的适用程度作了最集中和最形象的概括。微观粒子的量子态用波函数来描述,波函数随时间变化的规律就是Schrodinger方程,Schrodinger方程是量子力学中最基本的方程,其地位与Newton方程在经典力学中的地位相当。在不同的势场作用下,求出Schrodinger方程的解析解比较困难,对有些势场(如wood-Sxaon势,一维模型势等)要严格求出其解析解几乎不可能。为此,本文借助计算机编程,以有限深方势阱为例来求Schrodinger方程的数值解,并将结果与解析解进行比较,为求解Schrodinger方程提供一种简捷的方法。
1 Schrodinger方程的引入
与具有一定能量E及动量p→的粒子相联系的波是平面单色波,其表达式是

将上式对时间及坐标求导,并利用自由粒子的能量动量关系 E=p2/2m,可得
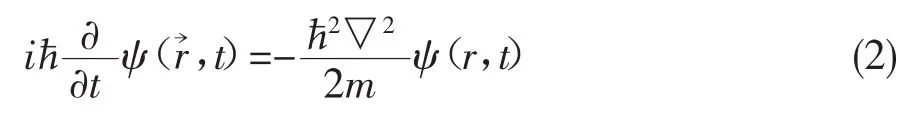
如果粒子在势场中运动,经典粒子的能量动量关系式是

作用于波函数上,即得


(5)式就是定态Schrodinger方程。

其中E是分离变量时引入的常数。方程(4)的解是

2 定态Schrodinger方程的解
2.1 有限深方势阱中的解析解
有限深方势阱[1]的表达式为:

在势阱内,Schrodinger方程为



奇宇称态

(10)和(11)是超越方程组,用图解法近似计算。在计算中取V0=1 000 MeV,a=4.0 Fm,m取质子的静止质量,mc2=938 MeV。可作出与方程组(10)和(11)对应的图 1和图2。在图1中,实线代表虚线代表 ξtgξ=η。在图 2 中,实线代表,虚线代表-ξctgξ=η。
从两曲线的交点坐标可算出,当V0=1 000 MeV,a=4.0 Fm时,各束缚态能级分别是E1=10.99 MeV,E2=44.51 MeV,E3=99.96 MeV,E4=176.85 MeV,E5=276.73 MeV。

图1 偶宇称态

图2 奇宇称态
2.2 有限深方势阱中的数值解
2.2.1 坐标空间的实稳定方法
实稳定方法是通过基展开的方法进行求解。它是基于这样的事实:在分立能区,各本征态 (束缚态)的能量不会随基空间的维数而改变;而在连续能区,本征态的能量多数会随着基空间维数的增加而逐渐降低,这些态对应于散射态;还有一些本征态能量随基空间维数的增加会出现一个平台,这些态对应于共振态[2]。实稳定方法也可以在坐标空间(离散的空间格点上)求解。通过改变坐标空间的大小,可以得到本征能量随格点数的变化关系。与基展开的方法类似,能量不随坐标空间格点数而改变的态就对应于束缚态,能量随坐标空间格点数的增加而减小的态就对应于散射态;而随坐标空间格点数的增加能量出现一个稳定的平台,再增加格点数,能量会逐渐减小,这样的态就对应共振态[3]。
2.2.2 数值求解过程
1)给定初始能量、两端初始波函数及其一阶导数值。
2)通过Runge-Kutta方法[4]向match点推近。
3)利用match点波函数是否光滑对接及节点数判断初始能量是否合适。
4)若节点数符合,波函数光滑对接,归一化波函数之后输出计算结果。
5)若节点数不符,则改变能量初值,重新进行计算,直到求得本征能量[5]。
2.2.3 数值计算结果
阱宽固定,阱深不断加深,数值计算得出各束缚态的能级如表1。阱深为V0=1 000 MeV,阱宽为a=4.0 fm时数值计算得到的前3级波函数如图3。
阱深固定,阱宽不断增加,数值计算得到的各束缚态能级如表2。
从表2中可以看出,当势阱的深度与宽度比较接近时,几乎找不到束缚态。而固定阱宽,当阱深加深时能级逐渐升高。当阱深加深到V0=1.0×106MeV时,它的各能级高度与无限深方势阱的各能级高度就相当接近了。可以推断,阱宽不变,继续加深阱深,各能级与无限深势阱的极限值将会相当吻合。
从表2中发现,固定阱深,宽度越小,能级越高,宽度越大,能级越低。而且各能级的能量值与阱宽a2基本上符合反比规律。从表1和表2中均可发现,当阱宽和阱深固定时,各能级的能量仍保持与量子数n2成正比的规律。

表1 阱宽,a=4.0 Fm,阱深由10~107MeV 变化时各束缚态能级 单位:MeV

图3 阱深为V0=1000 MeV,阱宽为a=4.0 Fm时的前3级波函数图

表2 阱深为V0=106MeV,阱宽由1.0~100.0 Fm变化时各束缚态能级 单位:MeV
3 两种解的比较
为说明数值计算方法的有效性,下面将V0=1 000 MeV,a=4.0 Fm,得出的解析解与数值解进行比较。表3中第2行为解析求解得到的能级,第3行为数值计算得到的能级。从表3中的数据可以看出,数值解得到的能级与解析解得出的结果基本上是一致的。数值求解不仅计算准确,更重要的是对于那些比较复杂的势 (如wood-Sxaon势,一维模型势等),根本无法求出其解析解,但用数值求解时,只要在程序中把势的表达式换一下,方程就可迎刃而解。因此,数值计算为求解Schrodinger方程提供一种简捷而有效的方法。

表3 两种解的比较 单位:MeV
[1]曾谨言.量子力学(卷Ⅰ)[M].北京:科学出版社,1995:101-105.
[2]Hazi A U,Taylor H S.Stabilization Method of Calculating Resonance Energies:Model Problem[J].Phys Rev A,1970,1:1109.
[3]张力,周善贵,孟杰,等.单粒子共振态的实稳定方法研究[J].物理学报,2007,56(7):3839-3844.
[4]聂铁军.数值计算方法[M].北京:高等教育出版社,1990:247-256.
[5]谭浩强,田淑清.FORTRAN语言程序设计[M].北京:高等教育出版社,1986.

