基于正交设计的旱区棉花膜下滴灌最优化探究

富 飞,贾志峰,张道媛

(长安大学环境科学与工程学院,陕西 西安 710064)

0 引言

旱区棉花的综合指标受到诸如自身品种、气候条件、土壤质地、灌溉定额、作物密度,生产资料投入等多种内外因素的影响。作为我国最大旱区的新疆生产建设兵团,其采用的棉花膜下滴灌技术,自 1996年在新疆石河子地区试验研究和应用以来,成效显著,目前滴灌面积已达 67万 hm2以上[5],成为世界上使用膜下滴灌最大的灌区之一。同时随着棉花膜下滴灌技术的应用,棉花“矮、密、早、膜”栽培技术优势得以进一步提高,膜下滴灌棉花的滴水量也比常规灌水量降低 50%以上。近年来,膜下滴灌棉花栽培密度也由 20万株/hm2增加至 28万株/hm2左右。对旱区广大职工群众而言,其最关心的是,如何用最小的滴水量,施以最少的生产资料投入,在保证棉花品质的同时,尽可能的在不影响籽棉产量的前提下,增大植株的种植密度。鉴于此,笔者以兵团职工群众最为关心的棉花品质指标单铃重、衣分、经济指标籽棉产量作为考查指标,根据新疆石河子炮台试验站 2008～2009年棉花膜下滴灌实测数据,采用正交试验法进行分析,从而为实现垦区棉花高产、高效、低成本提供科学依据。

1 正交试验法

1.1 正交设计法简述

正交试验方法是挑选部分有代表性的水平组合进行试验,通过对此部分试验结果的分析,以达到了解全面试验的目的,从而找出最优化水平组合,为生产实践服务。试验中把所要考察的结果称为指标,把对试验指标可能有影响的因素简称为因素,把每个因素在正交试验中要比较的具体条件称为水平[1]。正交试验有均衡分散和整齐可比的特点。本文以三因素,三水平为例,做简要分析。

1.1.1 均衡分散

指用正交表挑选出来的各因素水平组合在全部水平组合中的分布是均匀的。由图 1可以看出,在立方体中任一平面内都包含 3个实验点,任一直线上都包含 1个实验点,这些点代表性强,能够较好地反映全面试验的情况。

1.1.2 整齐可比

指每一个因素的各水平间具有可比性。因为正交表中每一因素的任一水平下都均衡地包含着另外因素的各个水平,故当比较某因素不同水平时,其它因素的效应都彼此抵消。

在实验中,一般首先根据实际情况,选择一张合适的正交表,记为 Ln(sr),L为正交表符号,n为试验总次数(行数),s为因素水平数(列数),r为最多可安排的因素个数[1]。在各因素给定水平下,通过正交表 Ln(sr),确定试验方案设计后,便可在此基础上,进行结果分析。

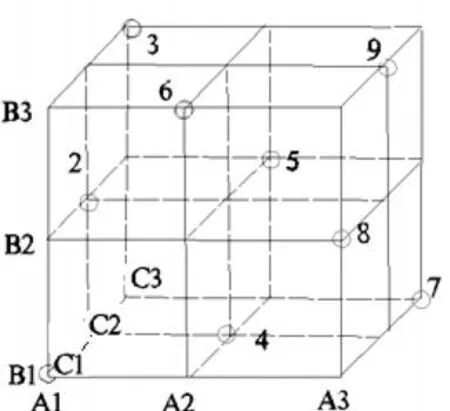
图1 三因素三水平试验的均衡分散立体图

1.2 正交设计结果分析

一般,对正交试验结果的分析通常采用极差分析法和方差分析法,在资料充分的情况下,还可以进行效应计算与指标的预估计。

1.2.1 极差分析法

通过极差 Rj的分析,可以确定因素变量 xi对指标 yi的影响主次顺序。求极差 Rj的方法如下:

设 A,B,…表示不同的因素,Ai表示因素A的第 i水平(i=1,2…,r),Xij表示因素的第 j水平的值(i=A,B…,j=1,2,…,na)。在 Xij下做了 n次试验得到 n个试验结果,分别为Yijk(k=1,2… ,n),则[2],

式中:Kij为因素i在 j水平下的各试验结果之和;m为因素 i在 j水平下的试验次数;Yijk为因素 i在 j水平下第k个试验结果指标值。需要注意的是,在多因素的组合试验中,不同的 i,j组合,有时可能是同一次实验结果。根据同一因素下,Kij值的大小,可以判断出该因素水平的优劣。

极差 Rj作为评价因素显著性的参数,其计算式为[2]:Rj=max{Kij}-m in{Kij}

Rj为第 j列因素的极差,反映了第j列因素水平波动时,试验指标的变动幅度。Rj越大,说明该因素对试验指标的影响越大。在分析极差之后,还可以绘制因素与指标的趋势图,据此可以更直观地看出试验指标随因素水平的变化趋势,为进一步试验指明方向。

1.2.2 方差分析法

极差分析法简单明了,但不能分析出不同因素水平下指标发生变异的原因,同时对各因素对指标的影响大小无法给以精确的数量估计。方差分析弥补了极差分析的缺陷,方差分析基本思想是将数据的总变异分解成因素变异和误差变异两部分,在此基础上,构造 F统计量,作 F检验,从而判断出各因素对指标作用的显著程度。具体步骤如下:

在正交设计方案 Xij下做了 n次试验得到 n个试验结果即 Yijk(k=1,2…,n),且 Yij1,Yij2…,Yijk相互独立,服从相同方差的正态分布,在正交表的指标列里,试验结果按顺序简记为 Yk～N(μk,σ2),求 Xij对指标 Yk的显著性影响,实际上就是对假设 H0:μ1=μ2=… =μn作显著性检验,其检验统计量构造如下:总偏差平方和

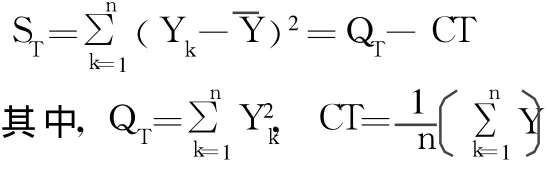
以因素 A为例,用 YAjk表示在 A因素下 j水平第 k个试验结果(j=1,2,3,…na),(k=1,2,…a)则因素 A的离差

和前述极差分析得:

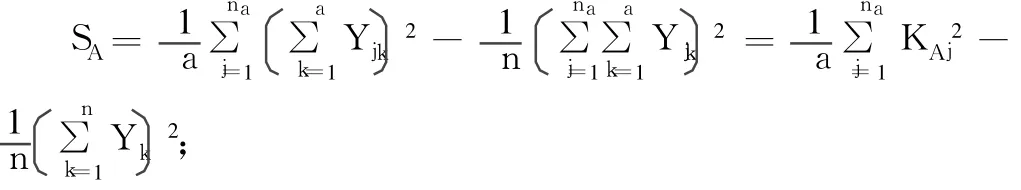
KAj即因素 A在水平下的各试验之和。ST反应了由因素水平的变化和试验误差引起的指标的差异程度。SA是正交表上第 j列所排因素 A的不同水平之间的差异程度,称为第j列 A因素偏差平方和;n为总的试验次数;ST的自由度 fT=n-1;Sj的自由度 fj=na-1。

用正交表安排计算时,应安排一定的空列将其空列偏差平方和当作随机误差平方和处理,由上述方法计算出 Se和fe,于是构造出统计量为第 j列的均

2 试验实例分析

2.1 试验地基本情况

该试验基地位于新疆准噶尔盆地南缘的沙漠绿洲过渡带炮台试验基地 ,地处北纬 44°51′,东经 85°15′,海 拔高度337.1m,属典型的内陆性荒漠化气候区域,试验田土质沙壤土,土壤肥力适中。在选择 9个小区时,尽可能选择相同耕作条件下,多年以来部分指标接近的田地为试验小区,以减少除研究因素之外其它因素的干扰。本次试验以作物密度A,滴水量 B,施肥量 C为考虑因子,各设三个水平,见表 1,利用正交表 L9(34),对其进行正交实验设计。表 2为正交设计方案及试验结果。

表1 因素水平表

表2 正交设计方案及结果

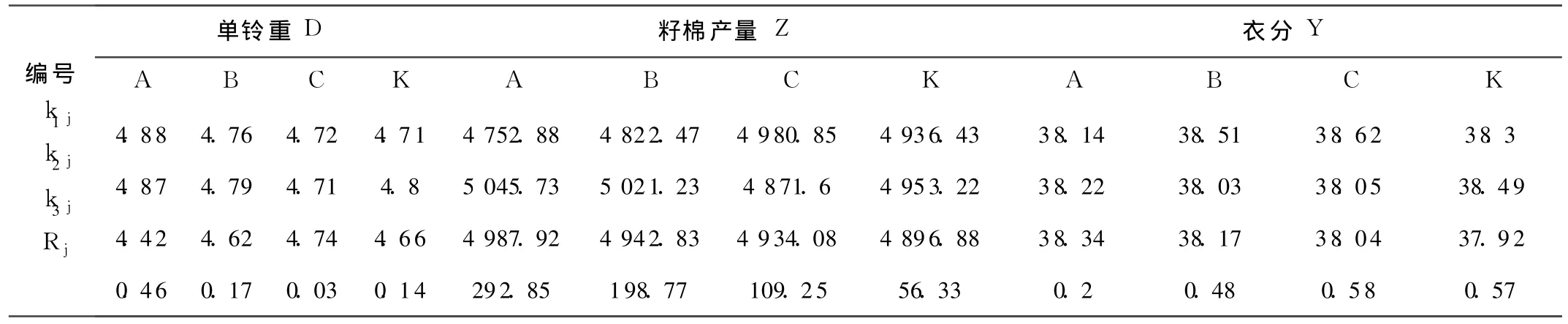
表3 各因素极差分析

由表 3极差分析计算可知,三因素对指标影响的主次顺序各不相同.对单铃重而言,其影响因素表现为密度A为主,滴水量 B次之,施肥量 C最后,各水平的最优化组合为A 1B 2C 3;因素对籽棉产量的影响是 A＞B＞C,各水平的最优组合是 A 2B 2C1;对衣分而言,影响因素的主次却表现出 C＞B＞A,最优化组合是 C1B 1A 3;显然这 3个方案不完全相同,对一个指标是好方案,对另一个指标却不一定是好方案。为此,我们以因素为横轴,指标为纵轴,采用[0,1]区间的归一化分析,其公式为:

图2 归一化处理后各指标随因子变化趋势图

归一化的最大优点在于将不同数量级的指标因子随因素水平的变化趋势反映在了同一区间,据此可以直观明了的分析出其变化趋势和最优组合。由图 2可以看出,密度作为影响籽棉产量和单铃重的最主要因素,其対衣分的影响却是次要的,当密度取水平 2时,其対衣分和单铃重的影响居中,对三个指标综合考虑,密度取 2水平,即 22.5株/hm2为好。水分作为影响旱区作物最重要的一个因素,在正交试验中,却并没像人们通常所想那样,滴水量越大,作物各指标便相应增加,相反,过多的水分对单铃重量和籽棉产量却表现出下降的趋势,误差因素在水平 2时影响不可忽视,对三个指标综合考虑,滴水量取 2水平,即 330mm为最优。由于在实验之前,为降低由于土壤质地不均等因素的影响,所选小区均为历年产量稳定,土壤较肥沃的熟地,故在本次试验中,除肥料对衣分影响占主导因素之外,对籽棉产量,却表现出低施肥,高产出的结果,不过通过对其趋势图的分析,不难看出,随着施肥量的增加,产量与单铃重在微小波动后,有上升的趋势,综合以上因素,在初步分析时,我们仍取 1水平即 1875 kg/hm2为最优组合。通过各因素对指标影响的综合分析,我们得出较好的实验方案是A 2B 2C 1.

方差分析回答了因素对指标影响显著与否及显著性程度。在因素对指标单铃重的方差分析计算表 4中,由于 Sc,Se,为提高 F检验的精度,故把 Sc并入 Se中,于是 SΔe=Sc+Se=0.0015+0.0315=0.033,fΔe=fc+fe=2+2=4,根 据 前述,对其他因素作统计量构造,(2,4)=18,故密度对单铃中的影响是高度显著的,FB和 F0.1(2,4)相差不大,在考虑误差存在的情况下,滴水量对单铃重的影响也是一个重要因素。施肥量对其影响不显著,其水平可以任选,在考虑经济成本的前提下,选水平 1,即施肥量1 875 kg/hm2为好。同上,分析三因素对籽棉产量的影响,19,FB＞F0.1(2,2)=9,故密度对籽棉产量的影响是显著的,滴水量对籽棉产量的影响较为显著,施肥量对产量的影响不明显。三因素对衣分的方差分析同单铃重,分析后知,FC=接近于 F0.1(2,6)=3.46,在误差占次要因素的衣分分析中,我们有理由相信,施肥量对衣分的影响较显著。综上方差分析不难看出,密度无论是从品质上(单铃重)还是从数量上(籽棉产量)对棉花的影响都是显著的,滴水量对上述二者的影响次之,施肥量按方差分析结果显示,对上述指标影响不显著,但考虑到误差因素和施肥对衣分的主导影响因素,施肥量取2 200kg/hm2左右为宜。

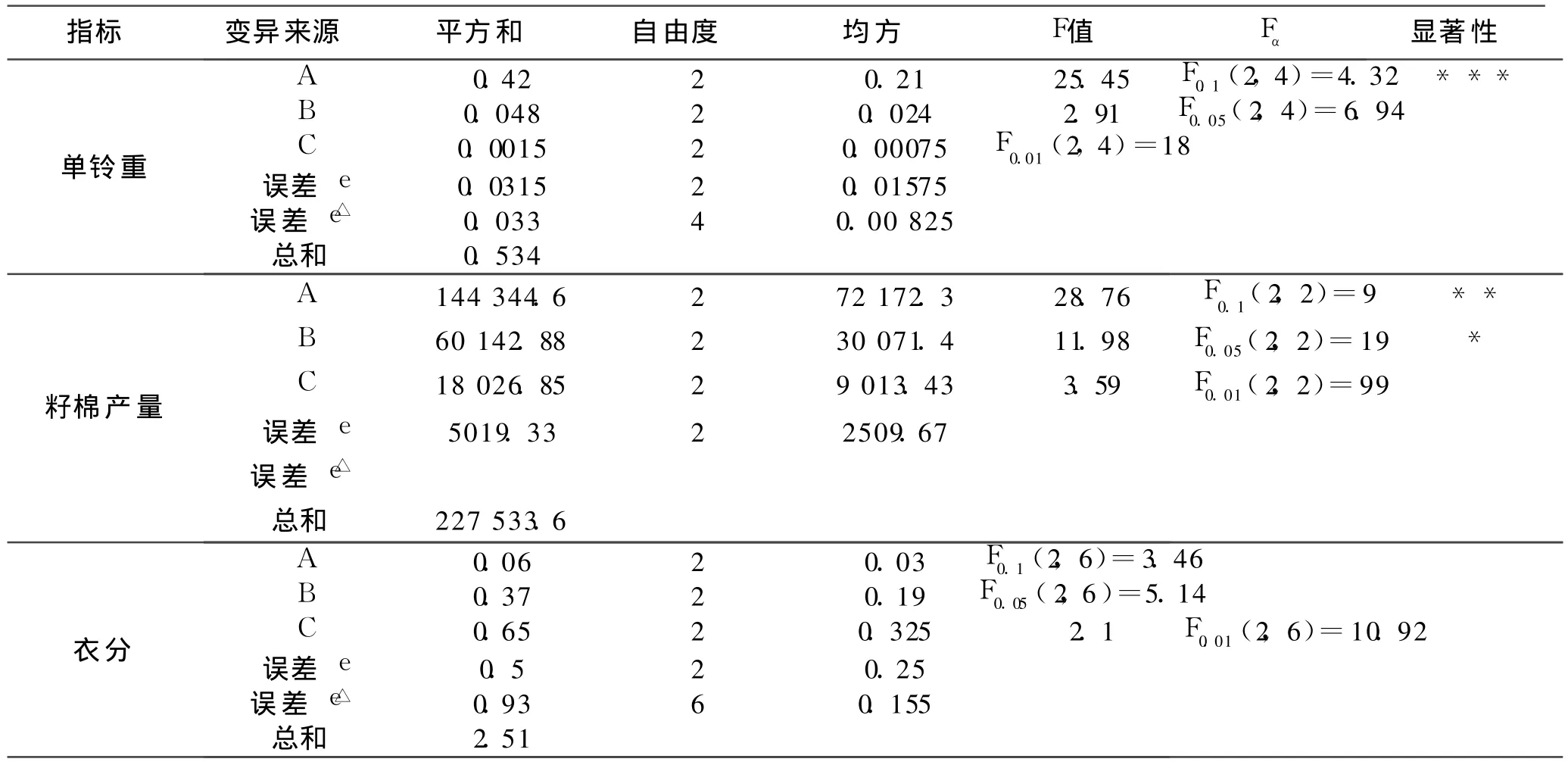
表4 方差分析表

3 结语

(1)正交试验的可操作性在于通过较少的试验次数,对全面试验有较多的了解。如本类周期长,试验规模大,投入人力较多的生产试验,正交设计方案的引入,无疑具有省时高效的现实意义。

(2)以正交方案分析数据为支撑,得出在膜下滴灌的新疆旱区,土壤肥力适中的情况下,22.5～25万株/hm2的高密度棉花膜下滴灌,滴水量在 330 mm左右,施肥量在2 200 kg/hm2的情况下,籽棉可达最高产量,同时在单铃重,衣分等品质方面也有所增加。

(3)试验以新疆准格尔盆地南缘炮台试验站基地为依托,对与其下垫面等因素相近的广大北疆旱区棉花生产有一定指导意义。实验虽然在宏观意义上对当地棉花生产的某些因素给出了参考值,但鉴于篇幅,没能从更多因素和指标上予以更全面的考虑。

[1]汪荣鑫.数理统计[M]。西安:西安交通大学出版社,2006.

[2]庄楚强,何春雄。应用数理统计基础[M].广州:华南理工大学出版社,2006

[3]罗传义.基于 Excel的正交试验方差分析程序 [J].计算机工程,2002

[4]蔡焕杰.荒漠区膜下滴灌棉花需水量和灌溉制度的试验研究[J].水利学报,2002,(11).

[5]张建新.不同灌溉量对膜下滴灌土壤水盐分布及棉花产量的影响[J].节水农业,2010