基于形态滤波的脉搏波信号基线漂移消除方法研究
刘艳丽, 赵为松, 李海坤, 汪方斌
(安徽建筑工业学院机械与电气工程学院,安徽合肥 230601)
0 引 言
脉搏中蕴涵着丰富的人体生理病理信息,其波形幅度和形态是评价人体心血管系统的重要依据,能够提供大量具有临床意义的早期诊断信息,因此对脉搏波信号的分析是了解人体心血管状态的重要手段。但是脉搏波具有一般生物医学信号的随机性强、信噪比低的特点,在人体表面采集过程中,不可避免地受到外界各种干扰,其中,基线漂移是各种噪声中对信号分析和诊断影响最大的,通常表现为缓慢变化的曲线,属于低频噪声[1]。为避免它对脉搏波信号分析和进一步处理时产生错误的影响,必须在预处理中对其进行消除。
目前,用于去除基线漂移的方法主要有滑动平均滤波、插值拟合法、自适应滤波、小波变换法等。滑动平均滤波是根据噪声信号和有用信号在频带分布上存在的差别,直接滤除低频基线漂移干扰,但该方法容易造成脉搏波信号的低频成分丢失,使滤波后的信号失真[2]。插值拟合法是以在脉搏波信号上找到的基准点为插值节点,通过函数拟合得到的光滑曲线估计出基线漂移,再用原始信号减去估计出的基漂信号,得到去除基线漂移后的脉搏波信号,该方法建立在正确识别基准点的基础上,对严重的基线漂移处理能力相对较弱,在实际测量过程中影响了处理的实时性。自适应滤波法需要一个与噪声有关而与信号无关的参考信号,在实际测量中运算较为复杂,难以满足要求。而小波变换法需要合理选取小波变换尺度使有用信号的频率成分与被抑制的干扰频率成分互不交叠,再用重构算法恢复去除基线漂移后的信号。由于该方法要用到小波的分解和重构,在实际应用中计算量很大[3]。
由于脉搏波中不仅含有人体自身在生命运动过程中产生的生理、生化信息,也有人体在受到外界环境刺激所产生的信息,因而具有重复性差和非线性的特点[4],一般的数字信号处理方法对其进行分析处理时存在一定的局限性。
本文根据脉搏波信号的形态变化规律采用了一种基于形态滤波运算的去除基线漂移的算法,以期在有效消除信号噪声的同时保留原信号的全局和局部特征,通过采用不同尺寸结构元素的开-闭和闭-开运算平均组合,滤除脉搏波信号中的基线漂移,该方法结构元素较短、运算量较小、耗费时间也较短,仿真实验结果表明该方法是有效实用的。
1 基本形态学运算和滤波
数学形态学是建立在数字图像处理方法和理论基础上的,其主要内容是设计一套变换、概念和算法,用于描述图像的基本特征[5,6]。
1.1 基本形态学运算
腐蚀和膨胀是数学形态学的2种基本运算,并引出开、闭及开闭的级联组合。形态变换分为二值形态变换和多值形态变换,全部形态变换的基础包括7种基本运算[7],即腐蚀、膨胀、开运算、闭运算、击中、细化和粗化等。
由于脉搏波信号是关于时间的一维信号,本文仅介绍腐蚀、膨胀、开运算和闭运算在一维信号处理中的定义。假定待处理的采样得到的一维信号为f(n),其定义域为:F={0,1,…,N-1},结构元素为g(n),定义域G={0,1,…,M-1},且N>M,则腐蚀运算定义为:

膨胀运算定义为:

由腐蚀和膨胀运算可以组成开、闭运算,分别为:

一般而言,数学形态学的开运算可用于消除孤立点,过滤信号上方的峰值噪声,去除毛刺等结构,使信号光滑;而闭运算可用于弥合孔洞和裂缝或将2个邻近的区域连接起来,用于平滑或抑制信号下方的波谷噪声。
1.2 形态学滤波器
在实际应用中,适当的形态运算组合可以用作形态学滤波。对信号进行处理往往采用形态开、闭的级联形式,文献[4]以不同顺序级联开闭运算,定义了传统形态的开-闭和闭-开运算,即

由于形态开的反扩展性和形态闭的扩展性,导致开-闭滤波器的输出幅度偏小,而闭-开滤波器的输出幅度偏大,为减小输出的单向偏移,可将开闭滤波和结果进行组合平均[7],由此定义的形态开闭-闭开滤波器为:

为进一步减小统计偏移现象,文献[8,9]提出了选用不同尺寸的结构元素的广义开-闭和闭-开滤波器,即

相对于传统的形态滤波器,广义形态滤波器可以更为有效地去除信号中的噪声。
1.3 结构元素选取
当信号的先验知识可以确定时,滤波效果不仅取决于运算方式的组合,还取决于结构元素的选取。信号中实际被滤除的成分,是由结构元素的选取决定的,结构元素的选取包括决定结构元素的形状、宽度和高度。考虑到脉搏波信号的特点和工程计算的要求,以及简化程序资源的需求,本文选取高度为零的直线形的结构元素,因为这样的结构元素在进行噪声消除的同时又能保持信号的形状。
2 脉搏波信号基线漂移消除算法
正常情况下,一个完整的脉搏波信号由升支和降支构成,包括主波、重搏前波、降中峡和重搏波,如图1所示。
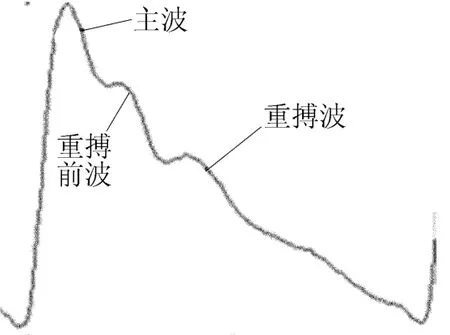
图1 正常脉搏波
受基线漂移影响的脉搏波信号可以看作是特征波形与缓变基漂信号叠加的结果,若对其进行适当的形态滤波,滤除其中所有与特征波形对应的波峰和波谷,即可分离出基线漂移信号。用原始信号减去基漂信号,可得到去除基线漂移后的脉搏波信号。
图1所示的脉搏波信号中,主波的振幅较高而占时较短,重搏前波振幅其次,重搏波振幅则相对较低,且3个波的波宽都较短。若直接采用较大宽度的结构元素,对脉搏波信号进行形态滤波,主波及重搏前波会被滤除,造成主波两侧区域基线估计的较大偏差,进而导致去除基线漂移后脉搏波信号的波形失真。为了尽量避免对后续处理造成不良影响,本文采用不同尺寸结构元素的开-闭和闭-开运算组合,校正基线漂移,整个算法结构如图2所示。

图2 去除基线漂移框图
算法步骤如下:
(1)对受基线漂移干扰的脉搏波信号x(n)进行广义形态闭-开滤波。根据波形特点选取不同长度和形状的2个结构元素,将x(n)与选取的结构元素先进行膨胀运算后进行腐蚀运算,将所得的结果再与结构元素进行开运算。
(2)对受基线漂移干扰的脉搏波信号x(n)进行广义形态开-闭滤波。即选取不同长度和形状的结构元素,将x(n)与选取的结构元素进行腐蚀运算后再进行膨胀运算,将所得的结果与结构元素进行闭运算。
(3)将进行了广义形态开-闭滤波和闭-开滤波的结果平均,即可得到与基线漂移信号有关的分量。
(4)用原始脉搏波信号x(n)减去估计出的基线漂移信号分量,得到基线校正后的信号y(n)。
3 仿真数据实验
为验证算法的有效性,以实验室所采集的脉搏波信号为原始样本,加入M IT数据库中专门提供的基线漂移信号bw,在Matlab平台上进行仿真实验,并对算法性能进行分析比较。
受基线漂移信号仿真数据模型为:

其中,x(n)为带有基线漂移的脉搏波信号;s(n)为通过屏住呼吸取得一段没有任何基线成分的纯净信号;b(n)为基线漂移信号。
图3所示为纯净的脉搏波信号s(n),图4所示为加入仿真基线后的脉搏波信号x(n)。

图3 脉搏波信号

图4 加入基线漂移后的信号
本文选用广义的形态开-闭和闭-开滤波器,选用的结构元素的宽度大于3个波的任一波宽宽度,宽度设为150、100个采样点。将带有基线漂移的脉搏波信号x(n)与长度为150个采样点和长度为100个采样点的直线形结构元素进行广义的形态开-闭和闭-开运算,得到估计的基线漂移信号,将它在x(n)中去除,得到如图5所示的基于形态学方法去除基线漂移后的实验结果。同时,也采用了小波阈值和基于经验模态分解的方法对脉搏波信号进行基线漂移的去除,去除结果如图6和图7所示。

图5 基于形态学去除基线后结果

图6 Emd去除基线后结果

图7 小波算法去除基线后结果
在信号去噪处理中,判断去噪效果的好坏主要有信噪比(SNR)和信号重构均方误差(MSE)2个标准。一般来说,SNR越大,MSE越小,则去噪效果越好。
均方根误差的定义为:

信噪比计算公式为:

其中,Pn为噪声方差;Ps为信号方差。
通过由小波、经验模态分解和基于形态学方法得到的信号均方根误差结果和信噪比结果,见表1所列。其中,信号原始的信噪比(SNR)为 13.526 0 dB。

表1 各算法结果比较
由信噪比和信号均方根误差可知,基于形态学的滤波去除基线的效果最好,采用小波和经验模态分解算法也能有效地去除基线漂移,但是采用小波阈值法存在较大的波形失真。因此,采用基于形态学的去除基线算法性能优于其它算法。
4 结束语
去除信号中的基线漂移干扰,是脉搏波信号预处理中的关键步骤。本文在总结了以往算法的基础上,提出了一种基于形态滤波运算的脉搏波信号基线漂移去除算法。通过仿真实验结果显示,与以往算法相比,这种滤波器在脉搏波信号处理中有较好的效果,关键是它在滤除噪声和去除基线漂移的同时,保留了信号中的有用信息。实验结果充分证明了该算法的有效性。
[1] 夏恒超,鲁永麒.一种新的基于三次样条插值技术的心电信号基线漂移消除方法[J].生物医学工程学杂志,2003,20 (3):524-526.
[2] 阴 玺,杨 浩,卞玉萍,等.一种改进的心电信号基线漂移矫正方法[J].计算机仿真,2007,24(11):107-109.
[3] 季 虎,孙即祥,毛 玲.基于小波变换与形态学运算的心电信号自适应滤波算法[J].信号处理,2006,22(3): 333-337.
[4] M arago P,Schafer R W.M orphological filters[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1987,35(8):1153-1184.
[5] 李向吉,丁润涛.脉冲噪声污染图像中的数学形态边缘检测器[J].中国图象图形学报,1998,3(11):903-906.
[6] 夏 静,胡茂林,卜华龙.一种基于Hop-A long的遥感图像道路提取算法[J].合肥工业大学学报:自然科学版,2009,32(12):1938-1940,1952.
[7] 唐常青,吕宏伯,黄 铮,等.数学形态方法及其应用[M].北京:科学出版社,1990:10-101.
[8] 欧阳森,王建华,宋政湘,等.基于数学形态学的电力系统采样数据处理方法[J].电网技术,2003,27(9):61-65.
[9] 白银钢,于盛林,李建明.一类新的广义形态开和广义形态闭滤波器[J].中国图象图形学报,2009,14(8): 1523-1529.

