基于空域追踪算法的基线漂移信号噪声修正*

谢芳娟，朱淑云

（南昌大学 科学技术学院，南昌330029）

基于空域追踪算法的基线漂移信号噪声修正*

谢芳娟，朱淑云

（南昌大学 科学技术学院，南昌330029）

为了消除基线漂移信号噪声对信号的干扰影响，提出一种基于空域追踪的修正算法.通过非线性滤波器从原始信号中粗提出基线信号，利用多步迭代微分算子从基线漂移信号中分解出更加精准的基线信号，再从原始信号中移除基线漂移信号，完成基线漂移信号噪声修正.选取多种类型测试数据（包括心电信号与噪声数据）来验证算法的有效性，结果表明，同传统的四种基线漂移信号修正算法相比，所提出的算法可以高效去除基线漂移信号的干扰.

基线漂移信号；心电信号；噪声信号；非线性滤波；空域追踪；微分算子；迭代运算；噪声修正

基线漂移信号（baseline wander，BW）广泛存在于各种信号采集过程中，是一种非线性、非平稳的波动信号.通常是由采集目标物理量受到外界干扰引起，常见的基线漂移信号首先存在于生理电信号采集领域［1－3］，例如心电、脑电，主要由病人的呼吸作用、身体挪动以及器械移动所引起；其次是存在色谱、质谱［4－10］领域，主要因实验条件以及使用样品的改变所引起；再者是存在红外光谱分析领域［11］，主要受空气波动等干扰造成.然而无论是什么成因，基线漂移信号整体上表征为一种混杂于正常采集信号中的低频噪声，该种噪声会影响正确解析以及判断采集信号，进而可能造成疾病误判、物质组分识别错误等严重的后果.作为信号质量保证的主要预处理操作，去除基线漂移信号对后续信号分析起到了重要作用.在过去几十年，也涌现出了众多基于不同理论的基线漂移信号修正方法.

基于线性滤波器，包括有限冲击响应（FIR）和无限冲击响应（IIR）滤波器的算法是滤除基线漂移信号的经典算法，其基于基线漂移信号频谱与目标信号谱带不同的假设，通过在频域设计通状阻带，移除原始信号中的基线噪声.但事实上，基线噪声信号和目标信号难以在频域上有明确的分界线，尤其是对于目标信号本身是时变非平稳的信号，谱带通常均会有重叠部分，难以固定截断频率，不能完全移除基漂部分，使得目标信号发生畸变，损失信号有价值的波群信息.非线性滤波器（例如中值滤波器）妥善地解决了线性滤波器固定截止频率的不足，可较好地移除基漂成分，但滤波器窗函数的截断误差给波形带来严重的“阶梯状”失真，在滤波精度要求严格的情况下，这种粗糙的滤波方式是难以接受的.因此，有学者引入了自适应滤波来修正基线漂移信号，这种方法在滤波过程中时刻动态调整滤波的截止频率，从而获得了较为理想的效果，但滤波实施的参照信号难以确定，不同的参照信号对结果也带来了不同的影响［12］.近年来，研究者尝试将滤波器结合信号分解变换等方式实现基线漂移信号的滤除，取得了不同的进展，如结合离散小波变换，利用小波变换检测奇异点或突变点的能力，可以完成对滤波器滤除基漂的近一步精确修饰，可以较好地保护各个波形的形态和幅值［13］.

空域追踪算法（NSP）［14］是一种利用微分算子迭代进行信号分解的算法，信号分解无需已知先验基波，便可将信号自适应地分解成一系列的调幅、调频信号的加权和.相关研究证明，运用NSP分解可有效地修正基线漂移信号，但这种直接利用NSP提取基线漂移信号的算法却同样面对处理耗时、计算量庞大的不便.本文提出结合非线性滤波和NSP算法的基线漂移信号修正算法，首先利用非线性滤波器粗提出一个基线轮廓，然后进一步结合NSP算法分解粗提的基线轮廓，从中分解出更加精确的基线漂移信号，这一分解过程可迭代多次以满足精度需求.在精度要求比较低的情况下，可快速得到基线信号，从而在计算准确性和时效性上达到平衡.

1 空域追踪算法

空域追踪算法是由Peng和Hwang［14］在其研究中首次提出的，其利用连续两次微分运算作为窄带信号算子TS，对信号进行自适应滤波，进而从原始信号中分离出一系列的调幅、调频振动信号.这一过程主要依赖信号自身的波形包络特点以及对应的频率特性，能够按照信号自身固有的振荡特点提取出原始信号的不同组分.基线漂移信号本身就是混合在采集信号中的一种噪声，其表现出低频、振荡以及类周期等特点，一个混有基线漂移信号的信号S可看做局部窄带信号与非窄带信号的叠加.空域追踪法正是利用单一局部线性微分算子，自适应地将信号S分解成S＝U＋V的形式，其中，V为局部窄带部分，即基线漂移信号成分，空域追踪法会将其分解到算子的空域中，完成对局部窄带信号的消除；U为非窄带部分，即希望保留的信号部分，其所有信息将不会存在于算子的空域之中.

将基线漂移信号看作局部窄带部分，则V＝S－U可被定义为一个长度为L的列向量，而二次微分算子TS根据泰勒级数展开原理会被转化成一个特定的矩阵，基漂部分V＝S－U会分解在TS的空域中，即TS（S－U）＝0.

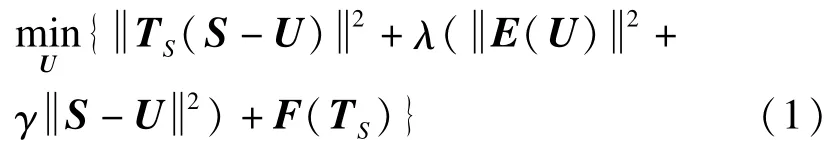
式中：E为一个用来正则化U的附加函数；λ为拉格朗日参数；γ为漏出系数，用来调节TS空域的解集区间，减少了空域追踪算法对最优化信号求解的贪婪性；F为调控算子TS的拉格朗日参数.通过求解式（1），利用自适应迭代算法将属于基线漂移信号的能量分解到算子TS的空域中.

在离散信号求解迭代中，S、U和α均为长度为L的列向量，则式（1）被改写为

式中：D为L×L的算子矩阵；Pα为对角线元素等于 α的对角矩阵；λ1，λ2为拉格朗日参数.通过给定和的值，便可求解出式（2）关于滤波后信号的最优解，其中可进一步改写为

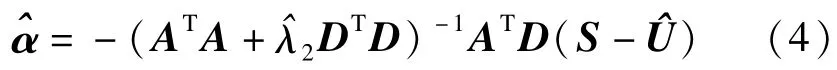
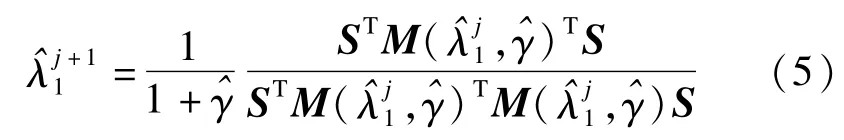
迭代过程虽在使用时是自动进行的，然而有学者［7］在其研究中也指出相关参数的选择会影响算法滤除基线漂移信号的效果，因此，对粗提基线漂移信号做进一步滤波，可获得更精确的信号.

2 算法描述

本文利用非线性滤波器来完成基线漂移信号的粗提，得到粗提信号后，进一步结合空域追踪算法得到更加准确的信号.可以选择的非线性滤波包括数学形态学滤波、中值滤波以及其他常见的滤波，文中以中值滤波为例进行算法描述和验证，具体步骤如下：

1）输入原始信号S0，将原始信号S0通过窗长为W的中值滤波器滤波，得到粗提后的信号S.

3 实验结果及讨论

为评价提出算法的效果，采用MIT／BIH心率失常数据库［15］数据对所述算法进行验证，选取MIT／BIH噪声数据库中两个真实基线漂移信号［16］，并将这两个噪声信号 B1和B2混入到受基线漂移信号影响较小的一段心电信号中，生成混合信号样本，即原始心电信号S1与S2.适合心电信号的λ1初值范围为10－6～10－5，每个数据样本均在此范围内对应不同的参数取值.

图1为S1采用不同滤波方法后得到的基线漂移信号对比.从滤波效果可以看出，采用中值滤波的基线漂移信号虽可以简单地提取出基线轮廓，然而却出现了台阶状的波形失真；而进一步采用NSP算法分解提取后，得到的基线漂移信号变得更加光滑，更贴近真实信号的波动形态.

图1 S1基线漂移信号比较Fig.1 Comparison in baseline drift signals for S1

图2 中给出了 S1滤除基线漂移信号前后的信号波形，可以看出原本存在于混合心电信号中的基线漂移成分被有效剔除了，且信号表征生理意义的波群被有效保存下来.

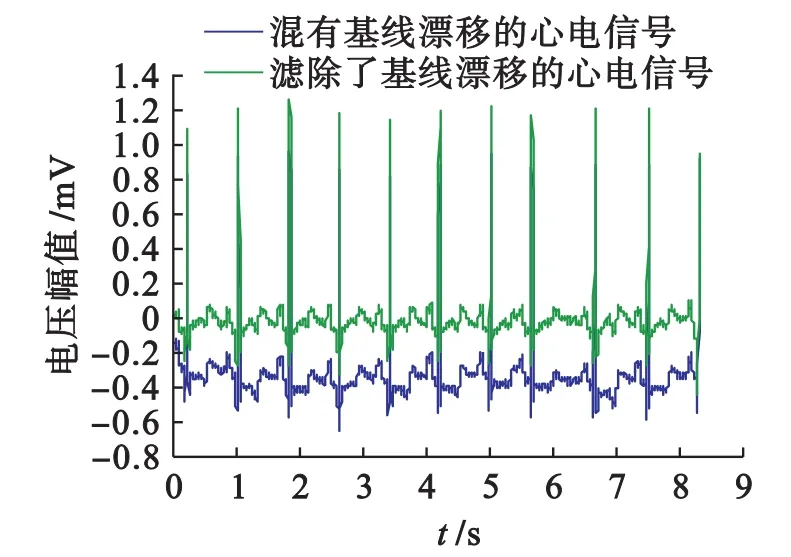
图2 S1滤波前后心电信号的比较Fig.2 Comparison in ECG signals before and after S1filtering

图3为S2采用不同滤波方法后得到的基线漂移信号对比，其整体表现与图1基本一致，均可从中值滤波粗提的基线轮廓中得到更加光滑的贴近真实的基线漂移信号.

图4中给出了S2滤除基线漂移信号前后的信号波形，从图4中可以看出，本文算法计算得出的基线漂移信号更加准确，且基线漂移信号被较好地移除.

图3 S2基线漂移信号比较Fig.3 Comparison in baseline drift signals for S2

图4 S2滤波前后心电信号的比较Fig.4 Comparison in ECG signals before and after S2filtering

实验证明，通过增加空域滤波，样本的滤波性能均得到了明显提升，滤波效果明显.下面给出验证该算法的3个评价指标，并且将其他4种常见滤波方法（单中值滤波、双中值滤波、卡尔曼滤波、带通滤波）与本文算法进行了横向比较.

基线漂移信号V与真实基线漂移信号B的相关度COR，其表达式为

基线漂移信号V与真实基线漂移信号B的差异信号的能量ENERGY，其表达式为

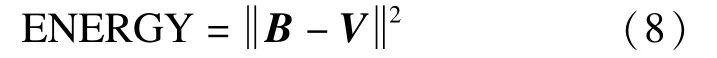
式（8）中差异信号能量占真实基线漂移信号B能量的比值RATIO，其表达式为

采用B1作为基线漂移信号混合到心电信号中，计算得到数据评价指标如表1所示.

从表1可以看出，本文算法在计算指标上均取得了最佳的表现.这里相关度COR表示了提取的基线漂移信号和真实基线漂移信号的相关程度，相关度约接近1，表示滤除的基线漂移信号和真实基线信号更加一致，而代表误差能量的ENERGY和比率RATIO则是越小越好，越小越能说明提取基线和真实基线信号每一点均接近.

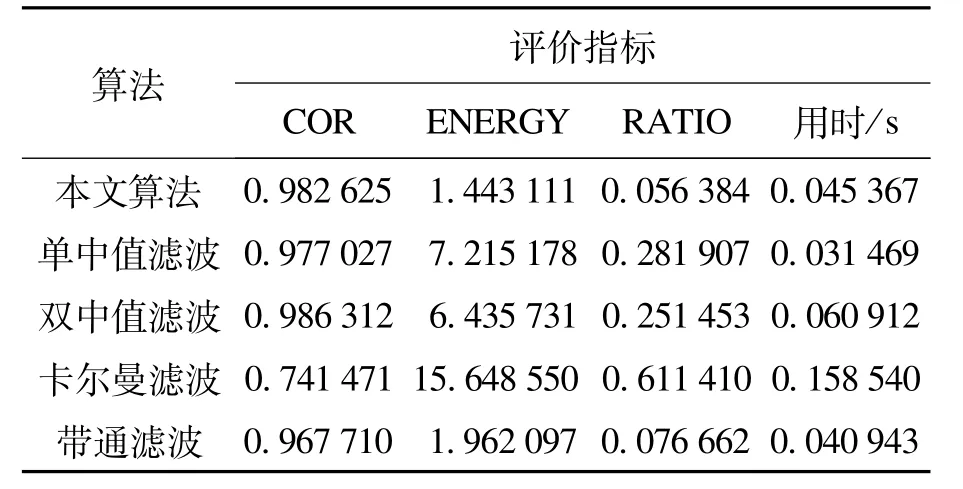
表1 S1信号相对于B1基线漂移信号评价结果Tab.1 Evaluation results of S1signals relative to B1baseline drift signals

同理，采用B2作为基线漂移信号混合到心电信号中，计算得到数据评价指标如表2所示.

表2 S2信号相对于B2基线漂移信号评价结果Tab.2 Evaluation results of S2signals relative to B2baseline drift signals

本文所提出的非线性联合均值滤波计算方法在准确提取基线漂移信号的基础上，提高了基线漂移信号的移除效率，同时在滤波稳定性上较文献［3］也有了较大的改善，可以提高计算效率.

4 结 论

本文提出了一种空域追踪的基线漂移信号修正方法，结合非线性滤波可以提升算法的效率和稳定性.借助空域追踪法对分离窄带信号的出色作用，成功地将算法运用到移除基线漂移信号的研究之中，并取得了良好的滤波效果.采用特定微分算子，自适应地将非线性滤波得到的粗提基线漂移信号进一步分解出精确的基线漂移信号，并将其引入到零子空间中，从而完成了基漂信号的移除操作.实验结果证明，所提出的方法可有效地去除基线漂移，并能保护待分析信号的有价值波群.

（

）：

［1］Mallick P K.Baseline drift removal of ECG signal：comparative analysis of filtering techniques［J］.IEEE Transactions on Signal Processing，2016，27（1）：151－160.

［2］庞宇，上官培阳，周前能，等.新型心电信号检测带通滤波器的设计［J］.重庆邮电大学学报（自然科学版），2015，27（2）：224－228.（PANG Yu，SHANGGUAN Pei-yang，ZHOU Qianneng，et al.Design of novel band-pass filter for ECG processing［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2015，27（2）：224－228.）

［3］Xin Y，Chen Y，Cui L.ECG baseline wander removal by null space pursuit［J］.Journal of Convergence Information Technology，2013，8（6）：1008－1015.

［4］范媛媛，桑英军，胡光，等.基于小波变换的电能质量监测［J］.沈阳工业大学学报，2014，36（6）：681－687.（FAN Yuan-yuan，SANG Ying-jun，HU Guang，et al. Power quality monitoring based on wavelet transformation［J］.Journal of Shenyang University of Technology，2014，36（6）：681－687.）

［5］尹波，郝宏刚，王斌，等.M IMO信道中空域相关特性分析［J］.重庆邮电大学学报（自然科学版），2013，25（2）：244－247.（YIN Bo，HAO Hong-gang，WANG Bin，et al.Analysis of spatial correlation of a channel model for M IMO［J］.Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2013，25（2）：244－247.）

［6］Baoa Q，Fengb J，Fang C，et al.A new automatic baseline correction method based on iterative method［J］.Journal of Magnetic Resonance，2012，218（5）：35－43.

［7］Gupta P，Sharma K K，Joshi SD.Baseline wander removal of electrocardiogram signals using multivariate empirical mode decomposition.［J］Healthcare Technology Letters，2015，2（6）：59－69.

［8］Xiong P，Wang H，Liu M，et al.Denoising autoencoder for eletrocardiogram signal enhancement［J］. Journal of Medical Imaging＆Health Informatics，2015，5（8）：1804－1810.

［9］Luz E JS，Schwartz W R，Chávez G C，et al.ECG-based heartbeat classification for arrhythmia detection：a survey［J］.Computer Methods＆Programs in Biomedicine，2015（127）：144－164.

［10］Kumar A，Singh G K，Anurag S.An optimized cosinemodulated nonuniform filter bank design for subband coding of ECG signal［J］.Journal of King Saud University，2015，27（2）：158－169.

［11］Gao QW，Zhu D，Sun D，et al.A denoising method based on null space pursuit for infrared spectrum［J］. Neurocomputing，2014（137）：180－184.

［12］Huang W，Cai N，Xie W，et al.ECG baseline wander correction based on ensemble empirical mode decomposition with complementary adaptive noise［J］.Journal of Medical Imaging＆Health Informatics，2015，5（8）：1796－1799.

［13］汤晓君，王进，张蕾，等.气体光谱分析应用中傅里叶变换红外光谱基线漂移信号分段比校正方法［J］.光谱学与光谱分析，2013，33（2）：334－339.（TANG Xiao-jun，WANG Jin，ZHANG Lei，et al. Spectral baseline correction by piecewise dividing in Fourier transform infrured gas analysis［J］.Spectroscopy and Spectral Analysis，2013，33（2）：334－339.）

［14］Peng S，Hwang W L.Null space pursuit：an operatorbased approach to adaptive signal separation［J］. IEEE Transactions on Signal Processing，2010，58（5）：2475－2483.

［15］Moody G B，Mark R G.The impact of the M IT-BIH arrhythmia database［J］.IEEE Engineering of Medical and Biology，2001，20（3）：45－50.

［16］Li ZM，Yang S X.Methods of removing the baseline wander in ECG based on the lifting wavelet transform［J］.China Medical Equipment，2014（3）：125－130.

（责任编辑：景 勇 英文审校：尹淑英）

Baseline drift noise correction based on null space pursuit algorithm

XIE Fang-juan，ZHU Shu-yun
（School of Science and Technology，Nanchang University，Nanchang 330029，China）

In order to cancel the interference influence of baseline drift noise on signals，a correction method based on the null space pursuit algorithm was proposed.The baseline signals were coarsely extracted from the original signals with a nonlinear filter，and more accurate baseline signals were separated from the baseline drift signals with the mufti-iterative differential operators.Then the accurate baseline drift signals were removed from the original signals，and the noise correction of baseline drift signals were accomplished.Various types of test data，including electrocardiograph（ECG）signals and noise data，were selected to verify the efficiency of the algorithm.The experimental results show that compared with the four traditional correction algorithms for baseline drift signals，the proposed algorithm can remove the interference of baseline drift signals with high efficiency.

baseline drift signal；electrocardiograph（ECG）signal；noise signal；nonlinear filtering；null space pursuit；differential operator；iterative operation；noise correction

TP 301.6

A

1000－1646（2016）06－0692－05

10.7688／j.issn.1000－1646.2016.06.17

2016－05－30.

江西省教育厅科学技术研究项目（GJJ151497）.

谢芳娟（1985－），女，江西兴国人，讲师，硕士，主要从事通信技术、信号处理等方面的研究.

11－07 12∶30在中国知网优先数字出版.

http：∥www.cnki.net／kcms／detail／21.1189.T. 20161107.1230.002.htm l