水平地震作用下框架高度对钢筋用量的影响*
张 培,朱 涵,赵 科,李自林
(1.石家庄学院经济管理学院,石家庄 050035;2.天津大学 建筑工程学院,天津300072;3.天津城建大学 土木工程学院,天津300384)
水平地震作用下框架高度对钢筋用量的影响*
张 培1,朱 涵2,赵 科1,李自林3
(1.石家庄学院经济管理学院,石家庄 050035;2.天津大学 建筑工程学院,天津300072;3.天津城建大学 土木工程学院,天津300384)
为了在建筑抗震设计中节省钢筋用量,提出了一种优化钢筋混凝土框架结构单位面积配筋量的方法.该方法探索楼层数m变化对构件内力分布和配筋量的影响,将一个矩形规则建筑作为研究对象,采用底部剪力法计算其在水平地震荷载影响下的构件内力,从而得到m与构件配筋体积之间的函数关系,进而转化为m与单位面积配筋量之间的关系.以m为优化变量,利用Matlab进行快速计算,并通过具体案例进行演示.结果表明,该方法具有一定的可行性,并得到m的最佳范围为6~11.
钢筋混凝土;框架结构;水平地震作用;底部剪力法;楼层数;梁;柱;钢筋用量
目前,环境污染早已成为了社会关注的重要问题,随着生产水平的提高,生产量的加大,由工业活动产生的大气污染与固体废弃物污染日益严重.我国正处于大力进行基础设施建设及城市化进程的过程中,因此,建筑行业必然成为重要的工业污染来源之一,同时建筑行业也是一个极度耗能的产业.有数据显示建筑业能耗为世界总能耗的40%以上[1];2013年的统计显示,石家庄PM 2.5年平均浓度为154μg/m3,空气质量达到及好于二级天数仅为49 d[2],可见减少建筑活动的影响刻不容缓.钢筋是使用最为广泛的建筑材料之一.2013年我国钢材产量为206 762.2万吨,钢筋产量20 619.2万吨.牛京考通过主成分回归分析法预测了中国2020年的铁矿石需求量为26.68亿吨[3],这些铁矿石也主要用于城市化建设及工业与建筑业.而经历地震作用后产生的建筑垃圾量也是相当惊人,建筑垃圾可在自然条件下发生化学反应释放有毒气体,并对大气环境产生不良作用[4].
由此可以看出,无论从钢材使用对环境的影响还是对资源的考虑,都应当在建筑抗震设计中尽量减少对钢筋的使用量.近些年,关于建筑抗震优化设计的问题多基于功能结构,采用依托可靠度的结构优化设计方法.但是在传统可靠度理论极限状态描述结构可靠与否的界限时,由结构可靠状态直接跳到失效状态,因此,一刀切的刚性失效准则既不科学也不符合工程实际[5].许多学者采用遗传算法、数学规划法和模糊结构优化法等方法寻找优化方案,例如,房占鹏等人以指定频带激励下振动响应峰值平方最小化为优化目标,约束阻尼材料用量为约束条件,建立约束阻尼结构的拓扑优化模型[6];郑山锁和杨威等人通过ANSYS建立被优化结构的参数化模型,调用遗传算法对结构进行工程造价最小化、失效模式理想化的多目标优化[7].这些方法多数是解决局部变量优化,或者需要高深数学原理,又或者无法在实际工程中推广.本文从一般性普通结构出发,运用基本的结构设计原理,完整计算整体建筑构件,并借助程序实现快速运算以找到合理结论,为最终确定性设计提供依据.
针对减少抗震设计的钢筋用量计算,本文在文献[8]的基础上仅考虑水平地震荷载的作用,将钢筋混凝土框架结构的楼层数m作为唯一变量,估算钢筋用量并观察其变化情况,以找到合理的m范围,确定钢筋用量较少的方案.
在设计过程中不考虑温度、收缩应力和构造要求等因素.结构计算是在满足截面承载力、挠度控制和裂缝宽度等要求下进行的,并且不存在特殊地质条件.设计过程为理想状态.
1 模型建立
采用钢筋混凝土框架结构为设计模型,其主要受力构件梁和柱通过节点区域刚接,柱下基础为刚性基础,从而形成了高次超静定体系[9].设定框架有m层,每层层高H相同,每层重力荷载代表值Gi相同(令 G=Gi),框架横向长度为 l,设计构件截面均为普通矩形截面.模型满足底部剪力法的计算条件,且不考虑顶部附加地震作用系数,采用底部剪力法计算.设计模型如图1所示.

图1 设计模型Fig.1 Design model
2 内力计算
框架水平地震力为

式中,α′1为地震影响系数.
框架各层节点集中力为
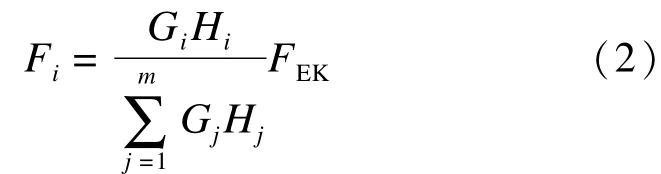
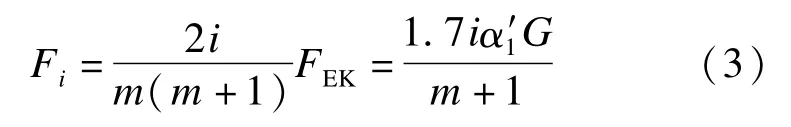
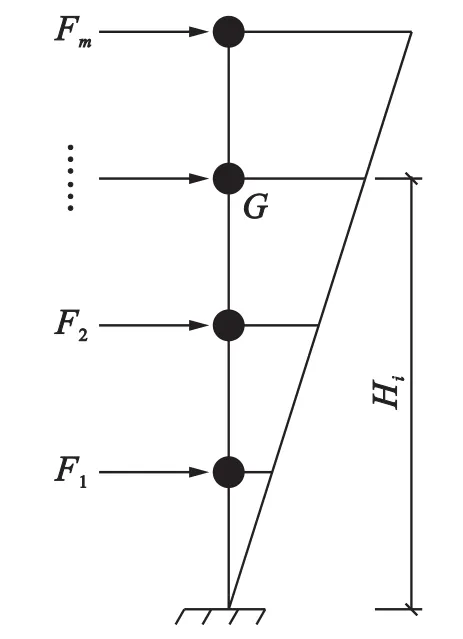
图2 水平地震荷载Fig.2 Horizontal seismic load
根据图2可得每层剪力,柱端弯矩和剪力的模型如图3所示,将第i层的剪力定义为Vt,其表达式为
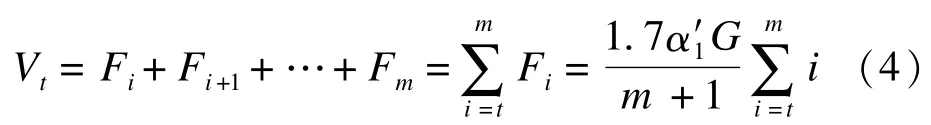
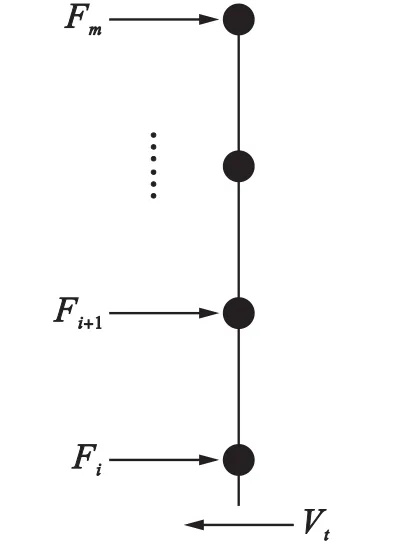
图3 柱的剪力平衡Fig.3 Shear balance of column
将第i层柱端的弯矩分别定义为Mct-up和Mct-down.采用水平荷载作用下内力近似计算的反弯点法选取力矩进行计算,上层各柱反弯点在柱中央处;底层柱反弯点偏离中央上移
由于在计算过程中主要以楼层数m为未知量,目的是考查随着m的增加,对整体结构钢筋用量的影响状况.在m增加的同时,上层不断增加,即计算的反弯点在柱中央的情况不断累加,而底层柱的数量没有发生变化,因此底层计算所占比重将越来越小.在底层柱子的计算中,反弯点的位置可以同上层各柱的情况,将反弯点在柱中央的位置统一为,该处理可使整个框架柱的计算更加方便简单,在公式协调上更加规整.
统一后,反弯点位置位于柱的中央,即柱的中点弯矩为零,柱的上下端弯矩分配于柱的两侧,且大小相等,如图4所示.
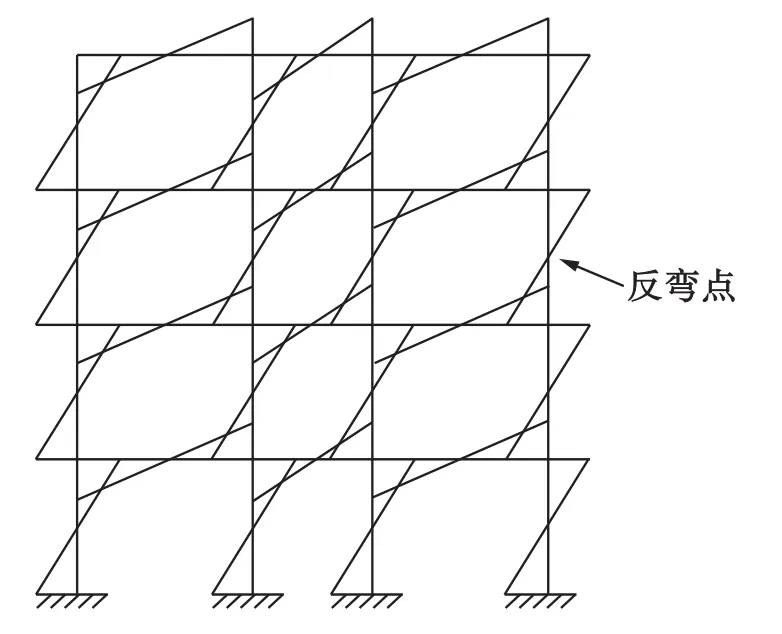
图4 框架水平力作用下的弯矩图Fig.4 Bending moment diagram under horizontal force action for framework

图5为梁内力计算图,其中,根据图5a可求得梁端弯矩,即

依据图5b可求得梁端剪力,即


图5 梁内力计算Fig.5 Calculation of beam internal force
图6为第i层柱的轴力,根据图6可求得单根柱第i层轴力为

为了清晰计算,以j代替t,重新整理轴力为
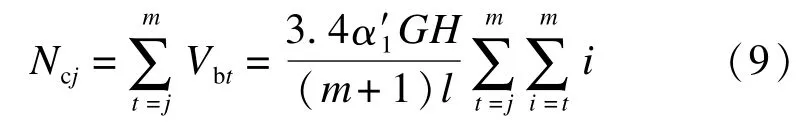
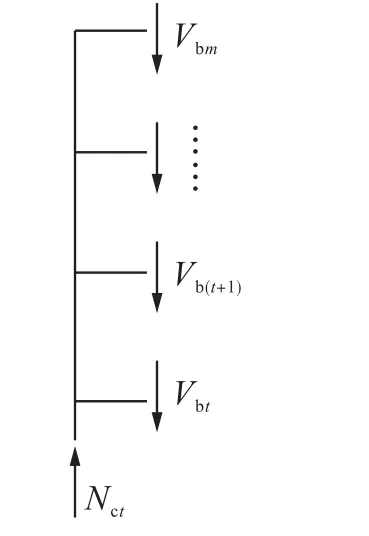
图6 第i层柱的轴力Fig.6 Column axial force of i-layer
3 构件设计
3.1 柱的配筋设计
3.1.1 纵向钢筋计算
偏心受压构件在不同荷载组合下,同一截面有时会承受不同方向的弯矩,在实际工程中,柱子的配筋以对称配筋为主[10].因此,本文将讨论对称配筋,并采纳大小偏心的界限破坏状态,即ξ=ξb,则大小偏心的受压钢筋面积As和受拉钢筋面积A′s的计算公式为
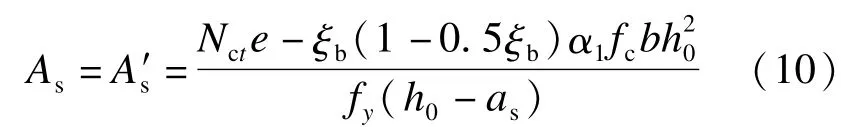
式中:e为轴向力作用点到受力钢筋合力点距离;α1为系数,与混凝土等级相关;fc为混凝土抗压强度设计值;b为柱横截面宽度;h0为柱横截面有效高度;fy为钢筋抗拉强度设计值;as为截面抵抗矩系数.
由于是估算,可认为纵筋通长布置,不考虑搭接等情况,则面积、长度及钢筋密度 ρs的乘积即为钢筋用量.单根柱纵筋质量为mcolumnl1=2AsHρs,一层纵筋质量为2mcolumnl1,一榀框架共m层,其质量为2mmcolumnl1.将整个框架划分成 n个网格,总质量为mcolumnl=2mnmcolumnl1.框架柱子纵筋总质量为
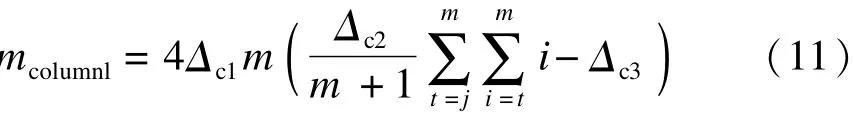
3.1.2 箍筋计算
柱子的箍筋设计计算公式为
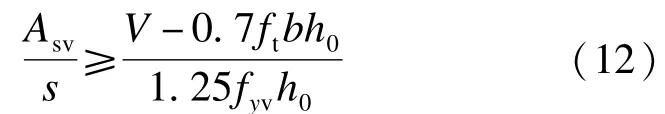
式中:Asv为箍筋钢筋截面面积;s为箍筋间距;ft为混凝土轴心抗拉强度设计值;fyv为箍筋抗拉强度设计值.
剪力V取上述中的Vt,为方便估算取等号计算,则有
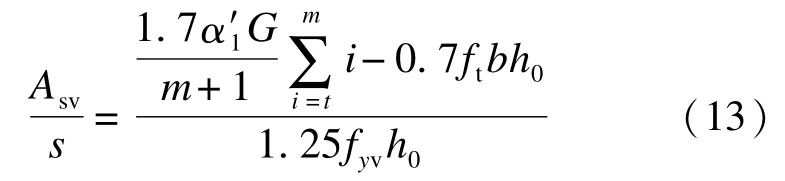
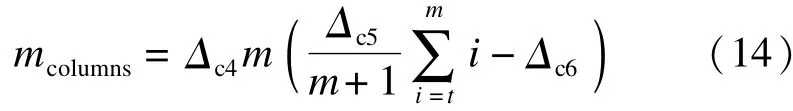
计算所得柱的钢筋用量为

3.2 梁的配筋设计
3.2.1 梁的纵筋计算
构件受到交变作用(如地震)易使截面上的弯矩改变方向,因此,将梁设置为双筋配筋,且认为受拉钢筋和受压钢筋的配置面积相同、型号相同.
梁纵筋面积计算采用的公式为
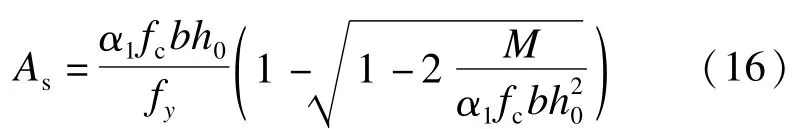
根据柱计算思路,梁纵筋同样通长布置,其长度为图1中的l,得到梁纵筋用量为
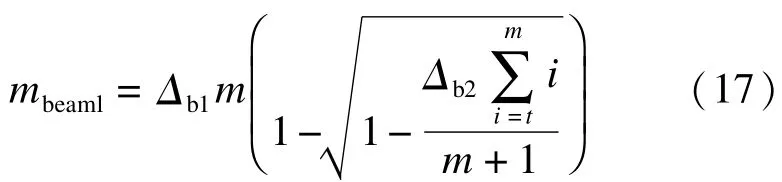
3.2.2 梁的箍筋计算
梁的箍筋面积计算公式为

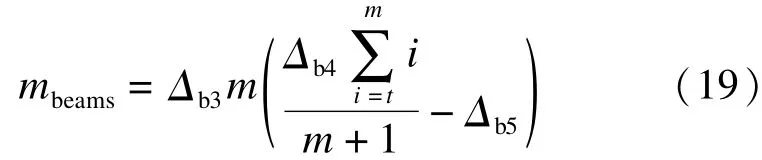
计算所得梁的钢筋用量为
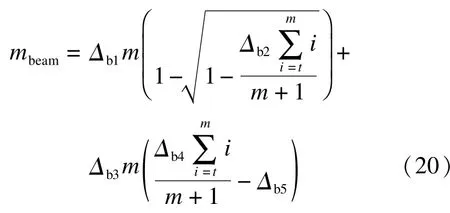
4 案例分析
某教学楼为钢筋混凝土框架结构.纵向长为18m,横向l为6.9m,楼层高度H为3m.梁、柱混凝土强度等级均为C30,梁、柱的主筋为Ⅱ级钢HRB335,箍筋为HPB235.地面粗糙类别为 B类,抗震设防烈度7度,Ⅱ类场地土,设计地震分组为第一组,抗震等级为三级.
楼面恒荷载为4.5 kN/m2,楼面活荷载为2 kN/m2.梁截面尺寸为250 mm×600 mm;柱截面尺寸为500mm×500mm.
案例中设定楼层数范围为 m=6,7,…,21,具体布局如图7所示(单位:mm).利用Matlab计算每种m值下的钢筋量,使用Midas设计软件,在相同设计条件下,统计每种设计方案的钢筋量.将两种方法所得的单位面积钢筋用量进行对比,并绘制成曲线如图8所示.
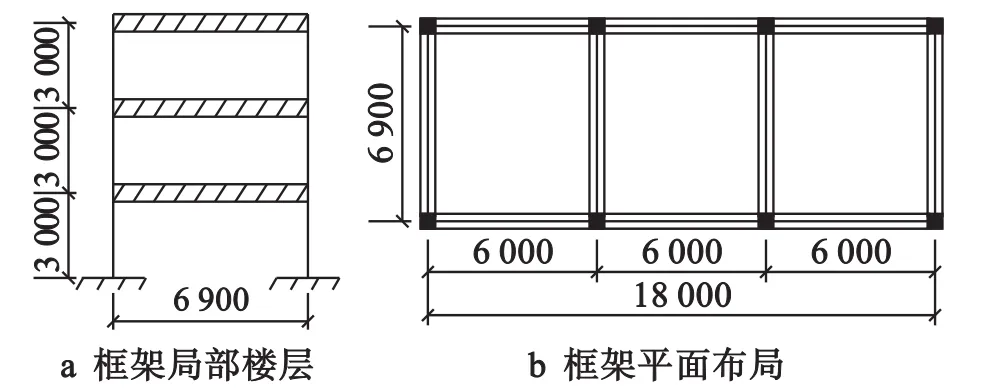
图7 案例布局Fig.7 Layout of case
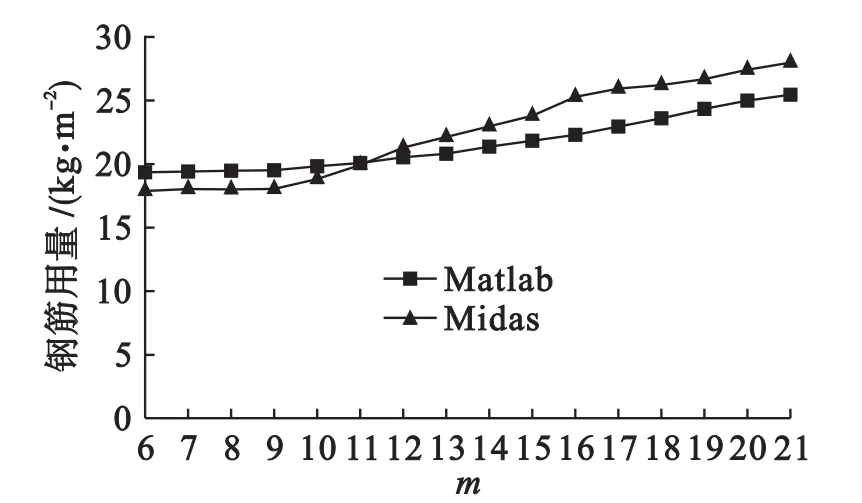
图8 m与单位面积钢筋用量关系Fig.8 Relationship between m and steel quantity for per unit area
由图8可知,Matlab曲线是根据公式所得,因此较平滑,而Midas曲线规律性则不强.对两种方法进行选择时,公式计算方法最大的优势是利用编程方法迅速得到规律性曲线,可从中找寻曲率关系;实际设计方法则需对每个方案进行分析,劳动时间和强度加大,且数据缺乏规律性.
两个曲线存在交叉点,并在交叉点之后曲线上升趋势加大,说明钢筋用量的增幅变大,且钢筋用量不断升高.因此,取交叉点之前的 m值是较理想的范围.
5 结 论
本文通过分析得出如下结论:
1)图8显示工程钢筋用量总体随m的增大而增大,但是m在6~11范围内,曲线没有较大浮动.因此,就本例而言无论是从抗震设计出发还是考虑钢筋用量都不提倡采纳高于11层的建筑.
2)文章公式基于结构原理,其推导存在若干假定,Midas计算结果更贴近实际.两者结果的变化趋势相同,两种结果较为吻合,说明公式推导方法是可行的,且编程计算速度的提高可加快实际工程方案比选的效率,对工程进度具有重要意义.
3)本文方法在选用的案例中得到了较好的验证,因此可作为进一步发展的基础,为类似研究提供参考.
4)若以Midas计算结果为依据,当m=6,钢筋总用量最少为18.26 kg/m2;m=21,钢筋总用量最多为28.18 kg/m2,可节约钢筋9.92 kg/m2.若按文献[11]计算CO2排放量,结果显示:原料开采与生产阶段m=6方案较m=21可降低25.79 kg/m2CO2排放量;成品加工阶段可减少2.35 kg/m2CO2排放量.由此可见,讨论资源节约和环境改善是十分必要的.
5)由上述结果可以判断,针对本文提出的案例,在水平地震荷载影响下,计算构件的单位面积钢筋用量随着楼层的增加而不断增大.同时钢材的CO2排放量与其用量息息相关,伴随楼层高度的增加也逐步上升.因此,不论出于荷载设计、耗材的考虑还是节能减排的研究,都不提倡设计较高层的建筑.
6)本文仅针对水平地震荷载作用对框架楼层高度产生的影响进行讨论,但在实际工程中的具体环境非常复杂,需另外考虑风荷载等影响因素进一步完善.同时在文献[8]中已经对框架的网格划分因素进行了分析,将其与本文的楼层高度因素进行综合考虑,可更加全面清晰地观察纵横方向两种变量对钢筋用量的二维影响.
(
):
[1]张小娟.国内城市建筑垃圾资源化研究分析[D].西安:西安建筑科技大学,2013.(ZHANG Xiao-juan.Studies and analysis on the resourcization of city construction waste in China[D]. Xi’an:Xi’an University of Architecture and Technology,2013.)
[2]中华人民共和国国家统计局.中国统计年鉴2014[M].北京:中国统计出版社,2014.(National Bureau of Statistics of the People’s Republic of China.China statistical yearbook 2014[M]. Beijing:China Statistics Press,2014.)
[3]牛京考.基于主成分回归分析法预测中国铁矿石需求[J].北京科技大学学报,2011,33(10):1177-1181.(NIU Jing-kao.Prediction of demand for iron ores in China based on principal component regression analysis[J].Journal of University of Science and Technology Beijing,2011,33(10):1177-1181.)
[4]王世镇.武汉市建筑垃圾与空气质量相关性及其对策研究[D].武汉:武汉科技大学,2015.(WANG Shi-zhen.Study on the relationship between Wuhan construction waste and air quality and its coun-termeasures[D].Wuhan:Wuhan University of Science and Technology,2015.)
[5]郑山锁,王晓飞,何伟,等.基于模糊可靠度的SRC框架结构优化设计研究[J].振动与冲击,2015,34(10):88-94.(ZHENG Shan-suo,WANG Xiao-fei,HEWei,et al. Optimization design for SRC frame structures based on fuzzy reliability[J].Journal of Vibration and Shock,2015,34(10):88-94.)
[6]房占鹏,郑玲,唐重才.指定频带简谐激励下约束阻尼结构拓扑优化[J].振动与冲击,2015,34(14):135-141.(FANG Zhan-peng,ZHENG Ling,TANG Zhong-cai. Topology optimization for constrained layer damping structures under specified-band harmonic excitations[J].Journal of Vibration and Shock,2015,34(14):135-141.)
[7]郑山锁,杨威,孙龙飞,等.基于遗传算法的型钢混凝土框架理想失效模式优化[J].工业建筑,2015,45(7):153-158.(ZHENG Shan-suo,YANG Wei,SUN Long-fei,et al.Optimization of the ideal failure model of SRC frame based on genetic algorithm[J].Industrial Construction,2015,45(7):153-158.)
[8]王万祯,苏仁权,王新堂.中等厚度高强钢缺口板断裂试验及数值分析[J].沈阳工业大学学报,2010,32(6):704-708.(WANGWan-zhen,SU Ren-quan,WANG Xin-tang. Fracture test and numerical analysis of high strength notched steel plate with moderate thickness[J].Journal of Shenyang University of Technology,2010,32(6):704-708.)
[9]卢明奇,杨庆山.矩形钢管混凝土柱力学性能非线性有限元分析[J].沈阳工业大学学报,2012,34(2):224-230.(LU M ing-qi,YANG Qing-shan.Nonlinear finite element analysis on mechanical behavior of concrete filled rectangular steel tubular column[J].Journal of Shenyang University of Technology,2012,34(2):224-230.)
[10]黄靓,王蓥,鲁懿虬.对称配筋钢筋混凝土小偏心受压构件简化计算方法[J].工程力学,2013,30(12):107-114.(HUANG Liang,WANG Ying,LU Yi-qiu.Simplified calculation method of symmetrically reinforced concrete members under small eccentric compression[J].Engineering Mechanics,2013,30(12):107-114.)
[11]张培,朱涵,刘春生.狭义物化能概念下建材CO2的排放量分析[J].安全与环境学报,2013,13(2):76-78.(ZHANG Pei,ZHU Han,LIU Chun-sheng.Analysis of CO2emission from the building materials in view of the embodied energy consumption[J].Journal of Safety and Environment,2013,13(2):76-78.)
(责任编辑:钟 媛 英文审校:尹淑英)
Influence of framework height on steel quantity under horizontal seismic action
ZHANG Pei1,ZHU Han2,ZHAO Ke1,LIZi-lin3
(1.School of Economics and Management,Shijiazhuang University,Shijiazhuang 050035,China;2.School of Civil Engineering,Tianjin University,Tianjin 300072,China;3.School of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China)
In order to save the steel quantity in the seismic design of buildings,amethod of optimizing the steel quantity for per unit area of reinforced concrete frame structure was proposed.The influence of the change in the floor number m on the internal force distribution and steel quantity of components was investigated.A rectangular and regular building was taken as the research object,and the internal force of components under horizontal seismic action was calculated with the base shear method,and thus the function relationship between m and steel volume of components were obtained,which could be further converted into the relationship between m and steel quantity for per unit area.Taking m as the optimization variable,the quick calculation was conducted with Matlab,and the demonstration was performed with a specific case. The results show that the proposed method has certain feasibility,and the optimal range of m is 6~11.
reinforced concrete;frame structure;horizontal seismic action;base shear method;floor number;beam;column;steel quantity
TU 51
A
1000-1646(2016)06-0715-06
10.7688/j.issn.1000-1646.2016.06.21
2016-01-15.
住建部基金资助项目(2015-K3-021);石家庄学院博士科研启动基金资助项目(13BS012).
张 培(1983-),女,山东济南人,讲师,博士,主要从事钢筋混凝土建筑结构优化等方面的研究.
09-07 16∶08在中国知网优先数字出版.
http:∥www.cnki.net/kcms/detail/21.1189.T. 20160907.1608.034.htm l

