基于精细解剖结构的左心室心肌缺血仿真

吕伟刚，王宽全，左旺孟，黎 捷，张恒贵

(1.哈尔滨工业大学计算机科学与技术学院，150001哈尔滨，lwg-2001@163.com; 2.曼彻斯特大学物理与天文学院，曼彻斯特，英国)

近半个世纪以来，心脏病已成为威胁人类健康最严重的疾病之一.根据中华人民共和国卫生部最新统计，2008年我国城市居民心脏病的死亡率已由2007年的第3位(仅次于恶性肿瘤和脑血管病)上升至第2位(仅次于恶性肿瘤)，而且仍保持上升趋势.其中心脏猝死造成的后果最为严重.大多数情况下，心脏猝死是由心律失常所导致［1］.室速和室颤是心律失常的两大类症状，往往发生在心肌缺血期间［2］.

TNNP模型是Tusscher等［3］于2004年提出的人类心室肌细胞模型，该模型基于新的实验数据，包括了所有主要的离子电流，在电生理特性和仿真性能上更接近人体的真实情况，因而更适用于复杂心室组织电生理活动的仿真研究.袁永峰等［4］研究了规则图形上的心肌缺血仿真研究问题，但是该模型存在2点问题:1)基于规则模型的仿真结果可能难以准确反映折返波在真实人体心室组织的传播过程;2)由于心室几何形状上的复杂性，因此规则图形上的边界求解过程不能直接应用在心室组织上.基于上述问题，本文引入精细的人体心脏解剖数据，同时考虑了心室肌细胞的电异质性，构建了一个整合的人体心室组织模型.在处理无通量边界问题上，使用相场法来自动计算复杂的边界条件［5-7］.

1 方法

1.1 心室组织模型

心肌组织是由许多单细胞互相电耦合而组成的一个电耦合胞体.在由心肌细胞组成的传导系统中，动作电位是通过偏微分方程来描述的.为了描述心室组织的电兴奋传导过程，使用TNNP模型，表述为

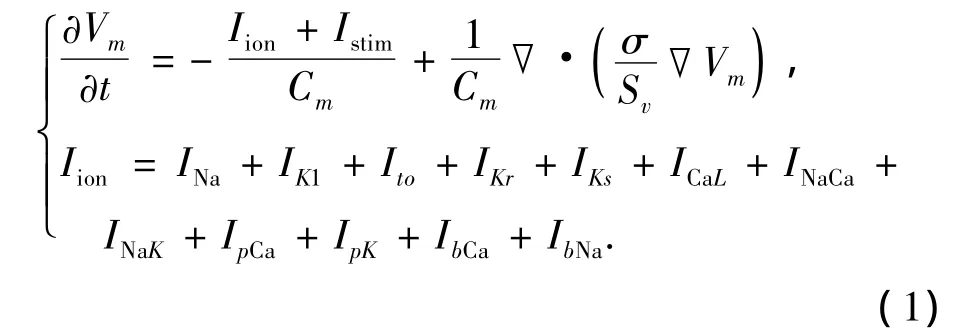
式中:Vm为跨膜电位，t为时间，Cm为跨膜电容，σ为电导率，Sv为面积体积比，也可写为， D为扩散系数，▽为梯度算子，Iion为跨膜离子流总和，Istim为所施加的刺激电流.

1.2 数值求解方法

心肌组织的电生理模型都需要满足无通量边界条件［8］，即n·D▽Vm=0，其中n为垂直于表面的法相矢量.其物理意义为没有电流流入或流出外部环境.

对于规则图形而言，在不考虑纤维走向各向异性的前提下，此时的边界条件问题可以简化为

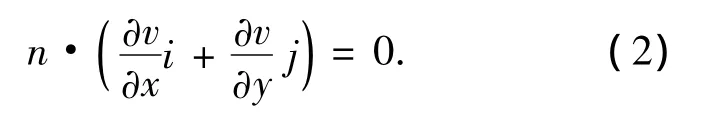
式中n⊥i，n⊥j.由式(2)可以得到边界点的跨膜电位Vm(x，y)=Vm(x-1，y)或Vm(x，y)= Vm(x，y-1)，即规则图形边界点的跨膜电位等于其内部沿x或y方向最近邻点的跨膜电位值.

但是对于精细的人体心室组织来说，由于其几何上的复杂性，计算边界点的法相矢量n并求解边界条件非常复杂且计算量大，在保证计算精确性的前提下就需要一个高效的方法来处理边界问题.这里使用相场法来自动计算复杂的边界条件.相场法是以金兹堡 -朗道相变理论为基础，引入新变量——相场φ而得名.

引入辅助域φ来区分心室组织的内外界，同时建立一个规则图形将心室组织容纳进去，其中φ=0为在心室外部，φ=1为在心室内部.

通过求解式(3)来确定φ值为

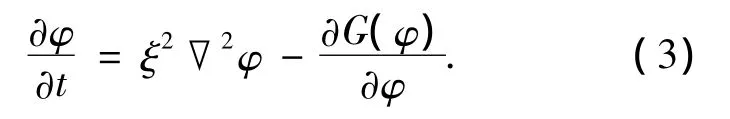
式中ξ为控制界面宽度的参数.当ξ值足够小时，无通量边界条件被满足，证明过程详见文献［7］. G(φ)是任意满足在φ=0和φ=1有最小值的双阱函数.这里，选择G(φ)为

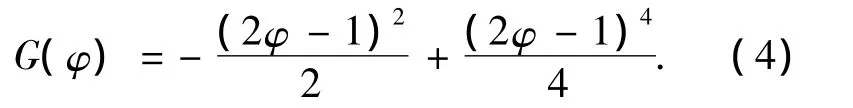
下面举1个简单的例子来解释φ随时间变化在不规则图形上的分布情况.建立一个100×100的正方形，内置一内径20，外径40的圆环，在正方形内对该圆环求解式(3)，当t=500 ms时刻的相值分布如图1所示.由图1可见，圆环区域内相值为1，在圆环边界处相值光滑且连续地从1变为0，圆环边界处外相值稳定为0.这样，利用相场法可以在不破坏计算精确性的同时直接使用规则图形的边界求解方法对复杂边界问题进行数值求解.由于使用了统一的控制方程来自动处理边界条件而无需跟踪，因而大大降低了计算复杂度.

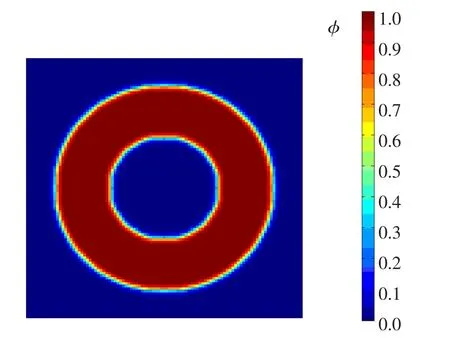
图1 相值φ在圆环上的分布(ξ=0.25 mm，Δx=Δy= 0.25 mm，Δt=0.015 ms，t=500 ms)

同理，由于在心室组织之外，跨膜电容Cm，跨膜电流(Iion+Istim)以及电导率σ并不存在，所以分别修正为 φCm，φ(Iion+Istim)以及 φσ，代入式(1)，可得

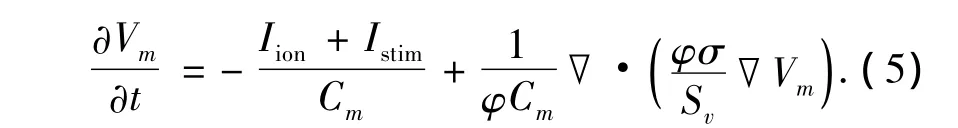
化简式(5)可变为

这里使用前向欧拉法求解式(6)，具体过程略.本文选择空间步长Δx=Δy=0.33 mm，时间步长Δt=0.02 ms，界面控制参数ξ=0.33 mm.

1.3 数据预处理

本文以美国“可视人计划”(Visible Human Project)解剖结构数据集为基础，提取了女性切片数据中的左心室三维数据，沿Z轴方向选择信息量较多的1片左心室组织.考虑到心室肌细胞的电异质性，按照距离内外边界的比例从内向外将心室壁分为3层结构:心内膜层、中间层和心外膜层.其细胞比例为4∶3∶4，这样就建立了人体左心室切片组织(如图2).

图2 分层后的人体左心室切片组织

2 结果

要研究心肌缺血下折返波的传播状况，首先就要激发出折返波.这里使用S1-S2协议，其中，S2刺激加在S1刺激不应期的尾部，S2和S1的强度2倍于阈值.

2.1 正常组织内的折返波

图3为正常的左心室组织内不同时刻折返波的传播过程.此时折返波没有遇到任何障碍，匀速平衡的传播.

图3 正常左心室组织内不同时刻的折返波形态

2.2 心肌缺血时的折返波

当心脏处于异常状态如心肌缺血的情况下，电兴奋的传播过程将受到影响.心肌缺血是心脏最常见的局部病理改变，其取决于缺血面积、部位、严重性等因素.当心肌细胞缺血时，发生的生理和病理变化有［9］:1)局部缺氧，ATP水平下降，酸性代谢产物积累，细胞内外环境酸化;2)因能量代谢障碍，膜离子泵功能下降，细胞外钾离子浓度(［K+］o)增高;3)胞内累积的脂质代谢物堆积到细胞膜上，影响离子通道蛋白与离子载体蛋白的活性;4)细胞内离子浓度失衡，Ca2+和Mg2+升高.

本文仅从缺血严重程度上探讨局部心肌缺血对折返波的影响，通过在缺血区域内增加［K+］o来仿真心肌缺血环境［10］.模拟的3种缺血情况分别为局部轻度缺血、局部中度缺血和局部严重缺血，对应的［K+］o值分别为7.5、9.0和11.0 mM，而正常情况下［K+］o为5.4 mM.

本文在左心室组织切片左上角设置一块大小约为30×30的不规则区域为缺血区域.如图4所示，I区为缺血区域，II区为健康区域，I区和II区之间的连接区域III区为过渡区.

实验发现由于心内膜细胞的动作电位持续时间太短，导致T波倒置，为了更接近真实情况，这里把其IKs通道的电导率GKs按照文献［11］调整为0.149 nS/pF，延长其动作电位时程.

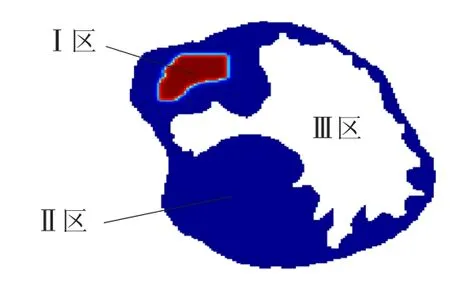
图4 缺血区域

图5～图7分别展示了在3种典型的时刻不同缺血情况下折返波的形态.

在t=1 350 ms时，由图5可以看到，折返波已经到达缺血区域，波前出现不同程度的缺口，这是由于折返波在缺血区域内的传播速度减慢所致.随着［K+］o升高，缺血区域对折返波的阻塞越来越大.局部轻度缺血如图5(a)所示的情况下，波前只是出现很小的缺口，缺血程度越严重，所出现的缺口越明显如图5(b)，(c)所示.

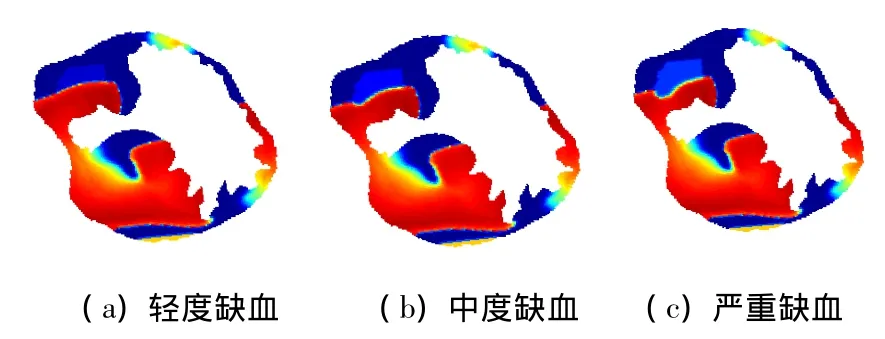
图5 不同局部缺血情况下同一时刻折返波形态(t=1 350 ms)

在t=1 400 ms时，由图6可以看到，局部轻度缺血对折返波影响不大，只是传播速度略微减慢，之后仍能穿过缺血区域继续向上传播如图6(a)所示.局部中度缺血的情况下，缺血区域内的波速明显慢于周围正常组织，但是折返波试图穿过缺血区域继续传播如图6(b)所示.局部严重缺血时，折返波已经很难穿过缺血区域，然而其周围的正常组织内折返波继续向上传播，这样折返波的传播发生很大程度的偏转如图6(c)所示.

在t=1 600 ms时，由图7可以看到，局部轻度缺血和中度缺血时，折返波已经完全穿过了缺血区域继续传播如图7(a)，(b)所示.局部严重缺血时，折返波在缺血区域处发生断裂，波前绕过缺血区域，汇合之后继续传播如图7(c)所示.

图6 不同局部缺血情况下同一时刻折返波形态(t=1 400 ms)

图7 不同局部缺血情况下同一时刻折返波形态(t=1 600 ms)

对比上述仿真结果，不难看出，缺血情况越严重，对折返波的影响越大.当缺血严重到一定程度的时候，折返波变得很不稳定，最终很难穿过缺血区域，这与文献［4］的研究结果一致.

同时，通过对正常组织和缺血组织的心肌细胞分析发现，缺血时期［K+］o的提高可以明显地影响缺血组织心肌细胞动作电位时程(APD).缺血越严重，缺血组织心肌细胞APD缩短程度越大.出现这种现象主要是由于［K+］o的提高在某种程度上增大了内部校正和延迟校正通道的传导速率，从而导致了APD的减小.即使折返波穿过了缺血区域，缺血组织心肌细胞的动作电位(AP)也已经发生了改变，这种改变使得动作电位空间不一致，引起各种离子以及代谢物的扩散.从电生理角度看，这些变化会改变心肌细胞动作电位的形态、兴奋性、传导速率等，进而导致心脏组织传导阻塞，这极大的不利于折返波的稳定传播，从而诱发心律失常.

3 结论

1)基于TNNP模型，考虑了心室肌细胞的电异质性，构建了人体左心室组织电生理模型，在处理无通量边界问题上，引入了一种高效的算法——相场法来求解.

2)通过设置缺血区域，同时在该区域内增加［K+］o仿真了局部心肌缺血情况下折返波在心室组织的传播过程.

3)实验结果表明，心肌缺血情况下，在缺血区域，折返波的传播受到影响.缺血程度越严重，折返波越不稳定，甚至会发生断裂现象.

4)通过分析实验结果发现，即使折返波穿过了缺血区域，缺血组织的心肌细胞动作电位也发生改变，导致动作电位的空间不一致性，这是诱发心律失常的本质原因.

［1］Ten TUSSCHER K H，BERNUS O，HREN R，et al. Comparison of electrophysiological models for human ventricular cells and tissues［J］.Progress in Biophysics and Molecular Biology，2006，90(1/3):326-345.

［2］HEIDENREICH E A，RODRIGUEZ J F，DOBLARE M，et al.Electrical propagation patterns in a 3D regionally ischemic human heart.a simulation study［C］// Proceedings of Computers in Cardiology 2009.Park City:IEEE，2009:665-668.

［3］Ten TUSSCHER K H，NOBLE D，NOBLE P J，et al.A model for human ventricular tissue［J］.American Journal of Physiology-Heart and Circulatory Physiology，2004，286(4):1573-1589.

［4］袁永峰，王宽全，田慧丽.二维人体心室心肌缺血模型中的折返波仿真研究［J］.生物医学工程学杂志，2009，26(6):1329-1334.

［5］KARMA A，RAPPEL W J.Quantitative phase-field modeling of dendritic growth in two and three dimensions［J］.Physical Review E，1998，57(4):4323-4349.

［6］FENTON F H，CHERRY E M，KARMA A，et al.Modeling wave propagation in realistic heart geometries using the phase-field method［J］.Chaos，2005，15(1):013502.

［7］BUENO-OROVIO A，PEREZ-GARCIA V M，FENTON F H.Spectral methods for partial differential equations in irregular domains:the spectral smoothed boundary method［J］.SIAM Journal on Scientific Computing，2006，28(3):886-900.

［8］CLAYTON R H，PANFILOV A V.A guide to modeling cardiac electrical activity in anatomically detailed ventricles［J］.Progress in Biophysics and Molecular Biology，2008，96(1/3):19-43.

［9］朱浩，尹炳生，朱代谟.基于单细胞电位计算心电:若干异常仿真心电图［J］.生物物理学报，2001，17(1):123-134.

［10］XU A，GUEVARA M R.Two forms of spiral-wave reentry in an ionic model of ischemic ventricular myocardium［J］.Chaos，1998，8(1):157-174.

［11］ZHANG H，HANCOX J C.In silico study of action potential and QT interval shortening due to loss of inactivation of the cardiac rapid delayed rectifier potassium current［J］.Biochemical and Biophysical Research Communications，2004，322(2):693-699.