多敏感器智能信息融合卫星定姿新方法
刘 梅,张 雷,武云丽,禹 航
(1.哈尔滨工业大学电子与信息工程学院,150010哈尔滨,thunder-ray81@hotmail.com 2.中国航天科技集团公司第五研究院,100029北京)
卫星姿态确定系统(ADS)是姿态控制系统的重要组成部分.卫星上天后,姿态确定正确与否,关系到卫星的测量控制精度和使用寿命.由于各敏感器基准的不同和产生误差的机理不同,必须通过信息融合技术、故障检测与系统重构技术来提高系统定姿精度和可靠性.这些技术对提高我国军用卫星的自主生存能力具有重要意义,拥有广阔的军事应用前景.同时,随着航天事业的发展,对卫星姿态确定的精度和可靠性的要求也越来越高.因此,如何利用多个信息源的融合来提高卫星姿态确定系统的性能[1],成为近年来航天控制中十分关注的重要问题.
联邦滤波是组合导航的主流算法,它根据信息分配原则保证了各子系统运算的独立和整体结果的最优,具有良好的容错性和较低的信息传输量,目前美国空军已将联邦滤波列为新一代导航系统的通用滤波器[2],如文献[3]中王志生等人采用的综合姿态确定系统,正是基于联邦滤波器开发而成的,实验证明该方法已经取得了较好的定姿精度.然而,现有的基于联邦滤波器的卫星定姿系统,一方面未考虑由于外界环境干扰及敏感器自身故障引入的污染数据对融合效果的影响,即缺乏必要的故障规避预处理环节,大大降低了融合定姿精度[4].文献[4]中对卫星姿态确定系统中故障规避环节的必要性进行了详细阐述,但其提出的聚类方法仍然需要较多的先验知识及经验;另一方面没有考虑各个敏感器工作状态的差异,即各敏感器的定姿精度不同,工作稳定情况不同,滤波得到的状态均方差不同等实际情况,仅采用一种固定的数据融合算法对各个子系统提供的数据进行融合,这样显然无法达到融合效果的全局最优,从而严重影响整个系统的定姿精度.本文针对上述情况,采用一种基于NFE模型(由模糊神经网络FN和专家系统ES构成)的多敏感器信息融合卫星定姿新方法,以提高卫星定姿的精度.本方法一方面引入波门检测预处理技术瞬时作出故障规避,对问题敏感器及时切断,阻止污染数据短时间内向下传播;另一方面,采用神经网络来构造具有学习、判断、推理、容错、自组织等高度智能化能力的模糊系统,用模糊规则对神经网络的训练进行指导,得到各个敏感器的置信度,以描述当时各个敏感器的工作状态.然后,在公共状态融合器部分依据各敏感器置信度的不同情况,对其提供的数据按照不同方法进行融合,使得整个定姿系统能随着敏感器工作状态的变化作出相应的判断.更加符合复杂定姿环境下的实际情况,从而提高定姿精度.
1 具有故障规避功能的多敏感器智能融合定姿复合结构
本文针对上述卫星定姿过程中存在的实际问题,以联邦滤波器为基础,加入波门选择器作为故障规避模块,采用惯性定姿敏感器—陀螺为公共参考系统,其余3个敏感器与陀螺两两组合作为子系统[5-6].其中3个子滤波器输出的公共信息为惯性测量组件,即陀螺的误差状态向量.通过融合算法选择模块对子滤波器输出的公共信息进行智能融合,得到陀螺误差向量的全局最优估计,最后用陀螺误差向量的全局最优估计对陀螺的输出进行校正,从而获得高精度的卫星姿态信息.
整个复合结构硬件方面由陀螺、星敏感器、红外地平仪和太阳敏感器组成;软件方面由故障规避模块、局部滤波器(子滤波器)[7]、主滤波器和智能融合算法选择模块组成一整套复合结构,其结构如图1所示.

图1 多敏感器融合定姿滤波器复合结构
2 基于波门预处理技术的故障规避模块
利用波门预处理技术,可以最大限度地滤除因敏感器不稳定及外界强干扰引起的污染测量值,从而保证参与融合的数据都是有效的.波门是一种有效的信息预处理方法,它是以测量值的预测值为中心构造一个搜寻区域,根据下一时刻的测量值是否落入该区域来决定此次测量值是否有效.通过自适应方法确定波门尺寸后,既可以保证落入波门中的有效量测有很高的概率,同时又保证了波门内没有过量的无效量测.波门尺寸的选择是否适宜,直接影响预处理的效果.波门过大落入波门内的虚警点会随之增多,相关逻辑也随之变复杂;波门过小,容易丢失真实量测值.因此,波门的大小应该由各个敏感器的量测误差决定.
本文采用的是一种基于测量残差矩阵和方差矩阵的自适应波门预处理方法.在这种方法中,波门的大小根据滤波所得的方差阵而自适应设定,既保证了有效数据落入波门的概率较高,又将污染数据隔离在波门之外.具体方法如下:
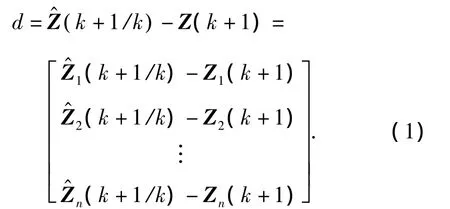

定义统计距离为
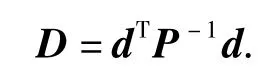
将式(1)和(2)代入,得到
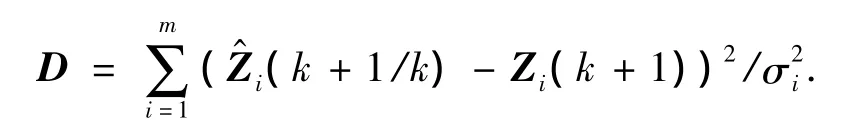
这样,在保证一定的正确数据落入波门的情况下,尽量减少了进入波门的污染数据的数量,降低误跟率,提高了跟踪效果,避免了不必要的计算量,更重要的是有效消除了因某敏感器发生短期失效产生的错误测量数据对整个融合过程的影响.
3 基于NFE模型的智能融合算法
置信度是衡量敏感器性能的一个重要指标,置信度可靠与否关系到最终系统融合结果的好坏.因此,系统要能全面的考虑各种情况,给出可靠的子系统置信度.在这个环节里,要通过定义计算各个子滤波器的置信度来判断各个子系统的工作情况.
本文采用模糊神经网络(FN)和专家系统(ES)构成NFE模型来计算敏感器的置信度.
置信度判别器神经网络是该系统的主要部分,该神经网络具有5层节点的神经模糊推理系统包含3个输入、1个输出和27条模糊If-Then规则.考虑到影响敏感器置信度的重要因素,选择3个输入的语言变量分别定义为:X表示敏感器状态,取值范围为[0,1],值越小表示敏感器状态越好;Y为敏感器检测概率;Z为敏感器虚警概率.且每个输入语言变量各有3个用高斯函数表征隶属函数的模糊集合.输出是表征某一敏感器置信度的实数值,其取值范围为(0,1),值越大表示敏感器的置信度越高.根据经验建立的模糊If -Then规则为:“If X is A1,and Y is B1,and Z is C1,Then‘置信度’is r1”,如表1所示.网络结构中同一层的节点具有相同类型的函数.

表1 if-then规则
采用混合学习算法对45个参数进行学习调整.当数据在网络中前向传输时,可采用最小二乘法辨识结论参数;当误差信号反转时,可采用最陡下降法来更新前提参数.这样辨识得到的结论参数是最优的,而且混合学习算法的收敛速度也是非常快的,通过画模糊神经网络的学习曲线可以看出:在第200次迭代时,误差在0.15左右,在第500次的时候误差基本收敛于0.1左右.
在得到了各个子系统提供的姿态角估计数据和各个子系统置信度的基础上,在公共状态融合器部分,可以依据各个子系统置信度的不同情况,对其提供的数据按照不同的方法进行融合.本文的3种融合方法分别对应卫星姿态确定过程中,主要影响定姿精度的3种实际情况:3子系统工作状态均良好;3子系统工作状态均不好;其中1个子系统工作状态远好于其他2子系统(即有2个子系统出现故障).当只有1个子系统故障时,本定姿结构仍可以利用另外2个正常工作的子系统互补长短,以取得较好的精度,因此不在此处考虑.其具体的方法主要有以下3种:
1)状态选择法.即选择置信度最佳的子系统提供的数据对公共状态进行修正.如果在定姿过程中,当两个敏感器由于自身故障或是外界干扰产生较大误差时,即其中1个子系统的置信度远远高于其他2个子系统,此时利用状态选择法可以有效的剔除故障数据,保留有效数据,从而保证系统的定姿精度
2)状态增强法.选择1个子系统作为系统状态,然后用其他的子系统状态对其进行修正.当各个子系统工作状态均不佳时,通过状态增强法可以使得各子系统互相修正,得到较小的随机误差,可保证整个定姿系统的定姿精度较高.
3)方差矩阵加权法.通过各子系统滤波后得到的方差矩阵Pi对最终的数据进行加权融合,即
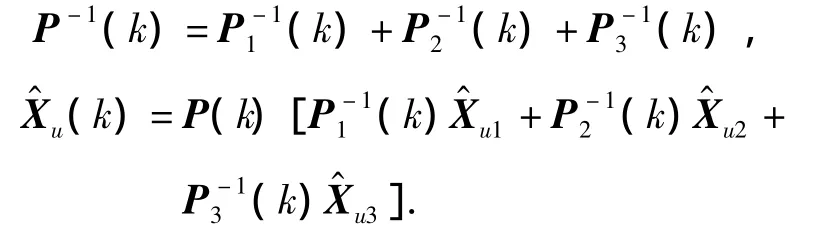
当各个子系统的工作状态都很好,即各个子系统置信度都很高时,通过方差矩阵加权法可以使得个子系统互补长短,从而进一步提高定姿精度.
其中在第3种情况下,也可以应用状态矢量加权法来进一步对融合结果进行优化.所谓的状态矢量加权法就是根据各个敏感器的权值,对它们的数据进行加权融合.在这里使用拉格朗日乘数法来推导相应敏感器的归一化权值.当每部敏感器的工作状态都较稳定时可采用此方法.此时,随机误差可被平均掉,故随机误差小.

其中ωi可以采用拉格朗日乘数法来求解.
4 仿真实验及结果分析
4.1 实验环境设定及实验目的
仿真时设定,陀螺仪常值漂移((°)/h)为(3,-5,-5),白噪声标准差((°)/h)为0.05,红外地平仪(GEO摆动扫描式)系统误差0.05°,随机误差0.03°,太阳敏感器测量误差0.05°[8],星敏感器测量误差9.9″,仿真时间300 s,在此仿真环境下做100次蒙特卡罗实验[9-10].
实验1:验证基于波门预处理技术的故障规避模块有效性.针对上述复合结构进行100次蒙特卡罗仿真实验,仿真时间取300 s,在其中随机选取80 s加入污染数据,以模拟由于外界环境干扰以及敏感器自身故障原因造成的数据污染,从而验证故障规避模块的性能.
实验2:验证基于NFE模型的智能融合算法有效性.实验共分两组,一组采用统一的方差矩阵加权法进行融合,另一组采用智能融合算法进行融合,分别进行100次蒙特卡罗实验,仿真时间都为300 s,以验证智能融合算法选择模块的性能.然后,在相同的仿真环境下,利用其他现有的定姿结构对卫星进行定姿,通过对比以验证本文提出的复合结构的定姿性能.
4.2 实验结果及分析
实验1:图2是各个子系统各时刻测量值相对于波门中心的归一化距离,通过本文给出的自适应波门门限确定方法可以得到最优门限为0.30.表2给出了最优门限(0.30)与人为设定门限值剔除污染数据的性能比较.
从图2中不难看出,当敏感器工作不正常的情况下即输出污染数据时,其测量值与波门中心的距离明显大于其他测量值到中心的距离,这就为本文提出的基于波门预处理技术的故障规避模块提供了可靠依据.从表2中数据可以看出:当波门门限值取得过小时虽然可以剔除污染数据,但是很多真实数据也被剔除掉了(真值落入概率小于100%);当门限值取得过大时,虽然保证了真实值落入波门的概率,但是许多污染数据无法剔除从而导致定姿精度严重下降;当门限值为通过本文方法得到的自适应门限0.30时,不但剔除了所有污染数据,而且保证了真实数据的落入概率,从而提高了定姿精度.
实验2:图3为本文提出的复合结构定姿精度,表3为各个时刻子系统的置信度和系统选择的融合方法,其中a表示状态选择法,b表示状态增强法,c表示状态矢量加权法.在同等仿真背景下进行定姿的横向比较,表4给出了各种敏感器组合以及复合结构定姿精度的比较.
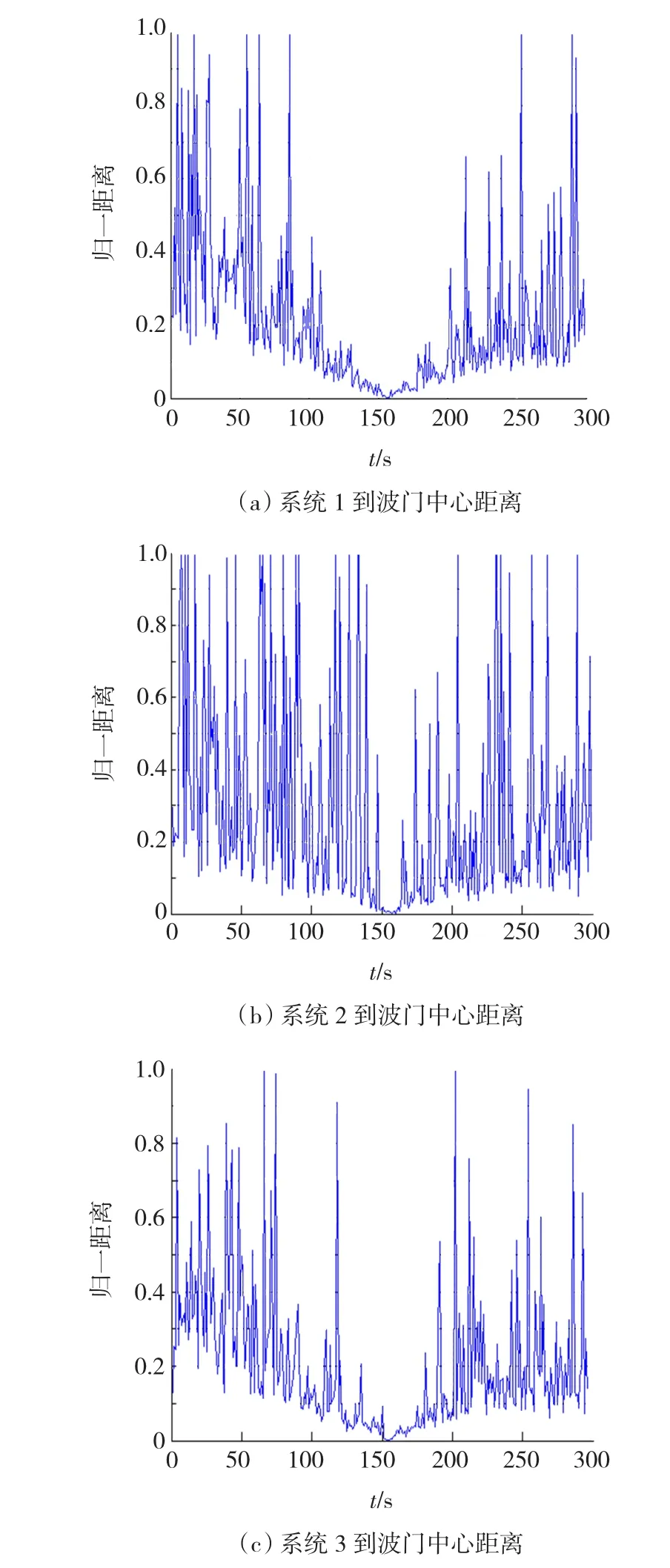
图2 各时刻测量值到波门中心的距离
由表3可以看出,本方法用置信度来描述各个子系统的工作状态和定姿精度,并根据前面设定的智能选择原则来选择相应的融合方法,以贴近实际的定姿环境.如在第一秒3个子系统的置信度均在0.7之上,都比较高,证明各个子系统的工作状态都很稳定,此时采用状态矢量加权法c进行融合,随机误差可被平均掉;又如第296 s,子系统3的置信度明显高于其他两个子系统,即其他2个子系统可能由于干扰和自身故障导致工作状态不稳定,此时系统智能选择状态选择法a进行融合,即选择置信度最佳的子系统提供的数据对公共状态进行修正,从而保证较高的定姿精度.可见,本方法可以根据定姿环境和敏感器工作状态的具体情况智能选择融合方法.由表4可以看出,复合结构的最终定姿精度高于现有定姿系统和未使用智能融合的复合结构(统一采用方差矩阵加权法)的定姿精度,可见在定姿系统中加入故障规避模块及融合算法智能选择模块使得污染数据得以剔除,并能够根据不同的敏感器工作状态智能选择相应的融合方法,从而提高了定姿精度.

表2 不同距离门限下的波门效果比较
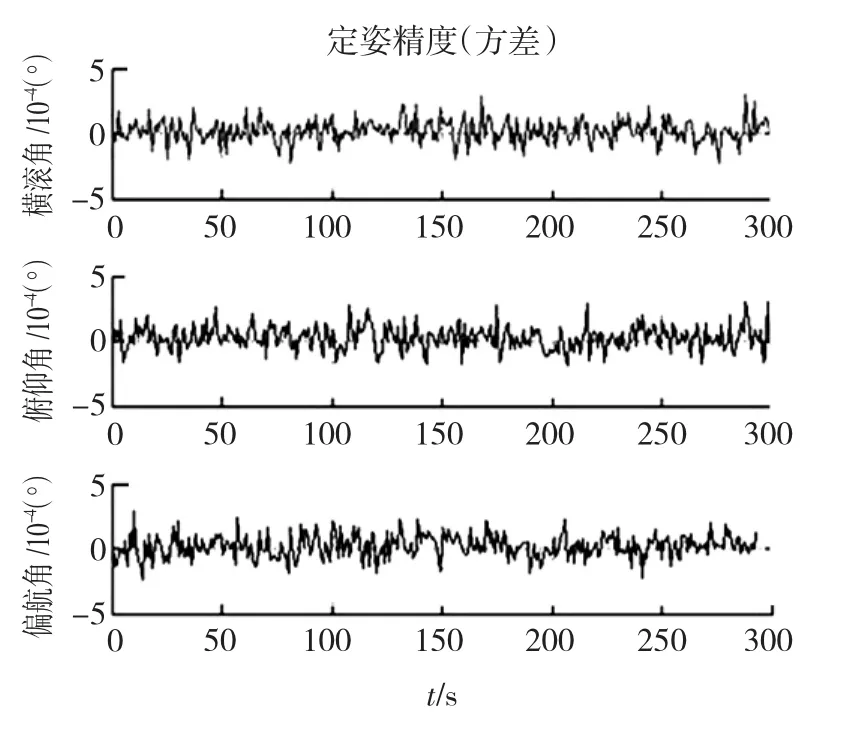
图3 复合结构仿真结果
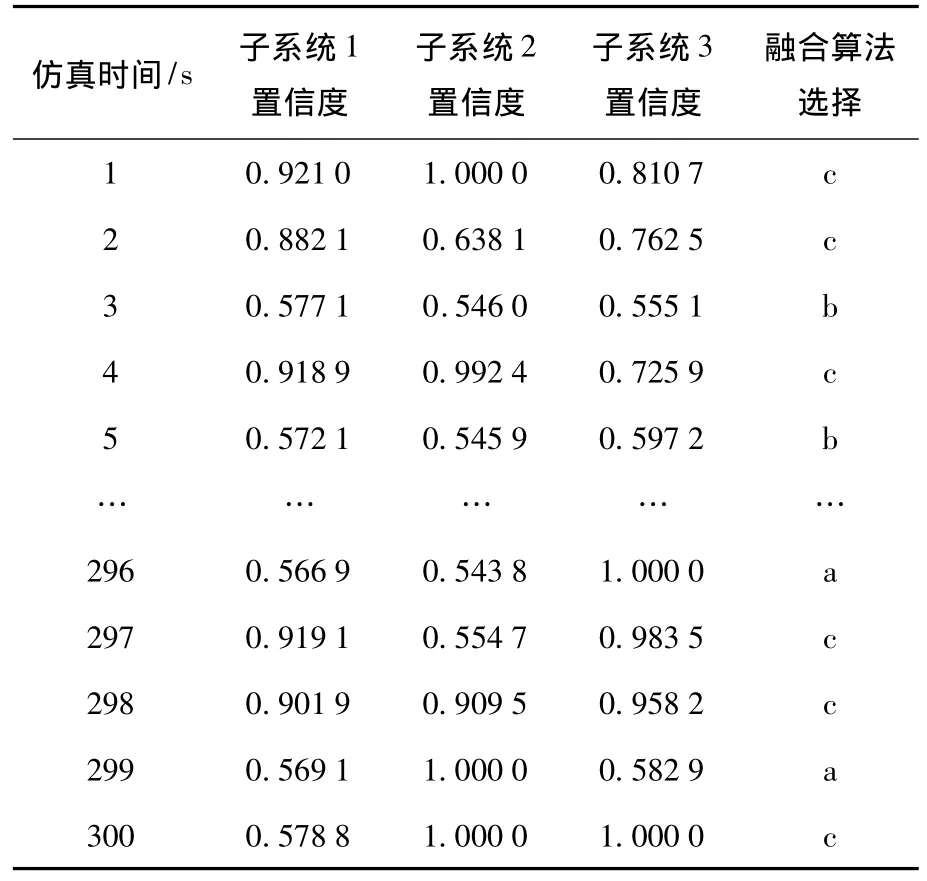
表3 各子系统的置信度和融合算法的选择
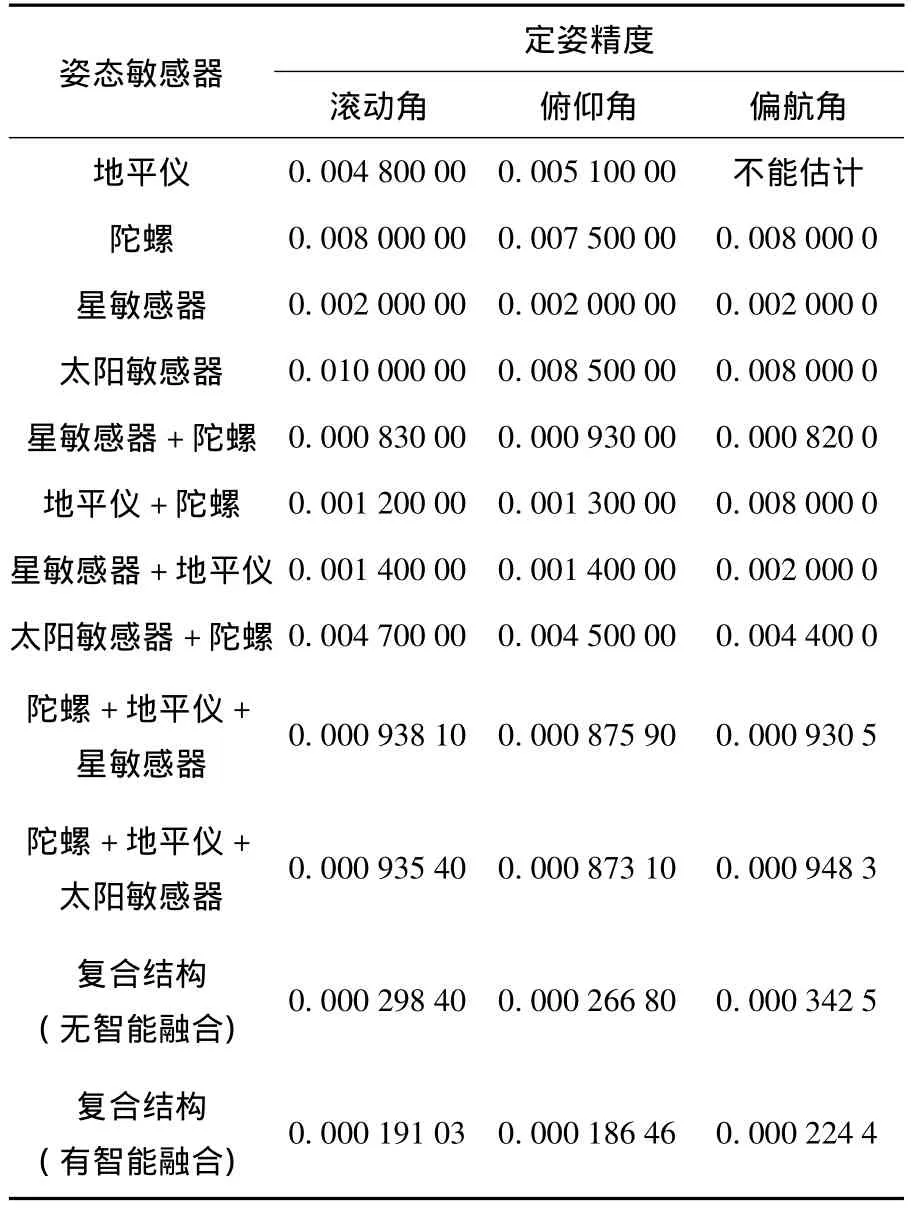
表4 各种定姿系统的精度比较
4 结论
本文针对配置多敏感器的卫星姿态确定系统,设计了以联邦滤波器为基础的高精度卫星姿态信息融合结构,提出了基于波门预处理技术的故障规避模块以及基于NFE模型的智能融合算法.本文设计的复合定姿结构,将不同敏感器组合提供的定姿数据进行融合,取长补短;利用波门技术剔除污染数据,保证参与融合的数据的有效性和准确性,从而达到最终融合的全局最优;并通过模糊神经网络和专家系统计算出各子系统姿态敏感器的置信度,以描述其工作状态,最后根据不同的情况选择相应的融合方法.通过实验证明,本定姿方法不但可以实现不同敏感器定姿信息的融合,而且可以剔除实际定姿环境中,因干扰及敏感器自身故障引起的数据污染,并能够随着各个敏感器的工作状态变化而智能选择相应的融合方法,从而实现更高精度的卫星定姿.
[1]DOWGIALLO D J,BOBAK J P.An economical and highly accurate attitude and position determination system for airborne polarimetric sensors[J].IEEE transactions,2008,10:1620-1622.
[2]OKATAN A,HAJIYEV C H.Kalman filter innovation sequence based fault detection in LEO satellite attitude determination and control system[J].IEEE transactions,2008,20:411-416.
[3]WANG Zhisheng.A new kind of satellite integrated attitude determination system[C]//Proceedings of 2007 IEEE International conference on control and automation.Guangzhou:[s.n.],2007:3254-3258.
[4]CAI Lin,HUANG Yuancan.A genetic-based fuzzy clustering algorithm for fault diagnosis in satellite attitude determination system[C]//Proceedings of 2003 IEEE Conference on Control Applications.Seattle:[s.n.],2003(1):115-119.
[5]GEBRE-EGZIABHER D,HAYWARD R C.Design of multi-sensor attitude determination systems[J].IEEE transactions on aerospace and electronic systems,2004,40:627-649.
[6]顾冬晴.多敏感器卫星姿态确定的联邦滤波器设计[J].中国空间科学技术,2004,24(3):7-13.
[7]OKATAN A,HAJIYEV C H.Kalman filter innovation sequence based fault detection in LEO satellite attitude determination and control system[J].IEEE transactions,2007,1:411-416.
[8]KUTLU A,HACIYEV C H.Attitude determination and rotational motion parameters identification of a LEO satellite through magnetometer and sun sensor data[C]// Proceedings of 2007 Recent advances in space technologies.Istanbul:[s.n.],2007:458-461.
[9]MORTON B P.Attitude determination and orbital estimation using earth position and magnetic field vector measurements[C]//Proceedings of 2004 American control conference.Boston:[s.n.],2004:4084-4089.
[10]LAM Q M,CRASSIDIS J L.Precision attitude determination usingamultiple modeladaptiveestimation scheme[J].IEEEAC,2006,9:1-20.

