基于小波阈值法的结构动力响应降噪处理

常 虹，张 冰

(1.吉林建筑工程学院，长春130021;2.吉林建筑工程学院城建学院，长春130111)

在环境激励下提取结构各结点加速度响应时，由于周围环境噪音的干扰及传感器自身的精度等影响，使得有用信号被噪声所淹没，因此为了获得有用信号，通常对所测得的加速度信号进行去噪预处理，剔除噪声信号.

1 小波去噪的基本原理

利用小波分析的方法进行去噪处理的实质就是将信号在不同尺度下作小波变换，即用不同中心频率的带通滤波器对信号进行过滤，得到信噪比较高的信号.在工程实际中，噪声信号通常表现为高频信号，而有用的信号通常表现为低频信号或比较平稳的信号.

设f(x)是实测得到的信号，采用Mallat算法，将信号在不同频率上作分解得:

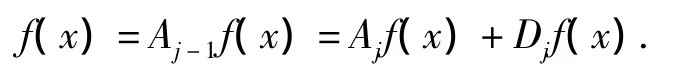
得到信号在低频空间的投影为:

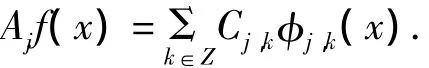
在高频空间的投影为:

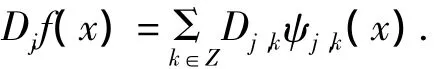
其中:Ajf(x)为信号中f(x)频率不超过2－j的成分，Djf(x)为信号中f(x)频率介于2－j与2－j+1之间的成分.

将上述的小波分解式写成矩阵形式有:

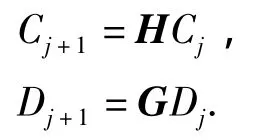
其中:j=1，2…J.上式即为Mallat塔式分解算法，其中H尺度函数对应的是低通滤波器，H= (hk－2n);G小波函数对应的是带通滤波器，G= (gk－2n);Cj在分辨率为2－j进行离散逼近，而Dj－在分辨率为2－j进行细节离散，{hk}k∈Z和{gk}k∈Z是一对离散的正交镜像滤波器，其中一个为低通一个为高通滤波器.

在对信号分解完以后需要对信号进行重构，Mallat重构的算法为:

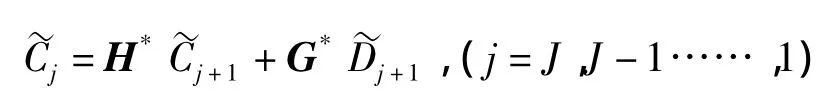
其中:H*为H的共扼，G*为G的共扼.

小波分析去噪方法实质就是通过Mallat分解，将实测的信号在不同频率范围内进行分解，然后再进行信号的重构，在进行重构时，将与噪声相对应的高频细节信号的系数置为零，从而达到去除噪音的目的，去噪后的信号表达式)为:

2 小波函数的选择

利用小波变换进行去噪的第一步就是选择合适的基小波，小波基的应用原理是利用其很少的非零小波系数去逼近特殊的函数，因此要选择能产生最多的接近零的小波系数的基小波，由于正交性、紧支撑性、正则性、对称性及消失矩等性质的不同，基小波的选择会对降噪效果产生很大的影响.要是信号是正则的同时小波函数又具有足够的消失矩，那么小尺度上的小波系数就会很小，实际工程中的信号没有完全正则的，通常都存在少数的奇异点，为了较少高幅值小波系数的数量，就必须减少小波函数的支集长度.因此在具体选择小波的时候，就面临消失矩和支集长度之间的矛盾.

为了对比哪一种小波的去噪效果更好，本文分别选取Db3、Db6、bior6.8、sym6、coif3、rbio6.8、dmey小波函数，对Benchmark模型在环境激励作用每层楼、一层的第24支撑发生损伤的情况下，提取结点15的加速度响应进行分析对比，比较各种小波函数去噪情况下的信噪比和均方根误差，见表1.

表1 不同小波函数降噪效果比较

从表1可以看出，bior6.8小波函数去噪效果最理想，信噪比最高均方根误差最小，Haar小波去噪效果最差.因此本文后面所涉及的去噪工作均选用bior6.8小波作为基小波.

3 最大尺度的选择

最大尺度越大被滤掉的噪声越多，对噪声分离是有利的，但在信号重构是丢失的细节信号也多，信号容易失真，因此最大尺度的选择必须合适.理论上可选择的最大尺度为J=［log2N］，其中［］代表向下取整，通过试验一般J取3～5比较合适.文鸿雁［1］在如何确定最大分解尺度时提出:逐渐增大尺度J，然后根据下式RMSE值的变化是否趋于稳定来确定J，

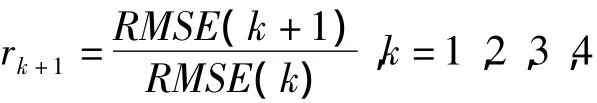
当J分别取1，2，3…时求得RMSE:通常总有r＞1，但当r≤1.1时认为噪声基本去除，这时J可取的最大尺度为k或k+1.

本文取Benchmark模型结点15的加速度响应，小波函数取bior6.8，当J取不同尺度时分别计算原始信号和估计信号之间的均方根误差，计算结果见表2.

表2 不同分解尺度信号均方根误差

由以上分析可得，当分解尺度取2时r＜1.1，因此本文小波降噪的最大分解尺度均取2.

在利用小波进行分解和重构滤波方法时，为了减小信号边界误差，在对信号进行降噪处理的时候需要对原始信号进行边界延拓.通常采取的办法有对称延拓法、周期延拓法和补零法.

4 非线性小波变换阈值法

4.1 算法实现

通常情况下，一维信号的非线性小波变换阈值去噪法主要有两种软阈值法和硬阈值法两种:

软阈值法:

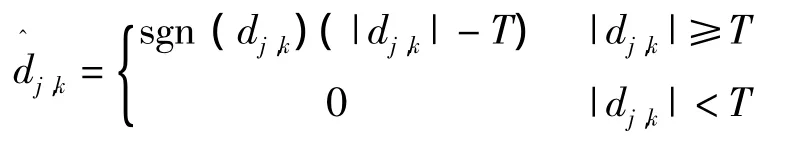
其中:dj，k为去噪前的高频系数为去噪后的高频系数，T为阈值.

4.2 阈值函数的选取

l)固定阈值(sqtwolog规则)

该方法的依据是N个具有独立同分布的标准高斯变量中的最大值小于T1的概率随着N的增大而趋近于1.

2)Stein无偏似然估计阈值(rigrsure规则)

该规则是采用基于Stein无偏似然估计原理的自适应阈值，该方法的去噪过程为:确定信号的长度N，设P=［p1，p2，p3，…..pN］，其中p1≤p2≤p3≤……≤pN，P的元素为小波包分解系数的平方并按照由小到大的顺序排列.定义风险向量R=［r1，r2，r3……rN］，其中:

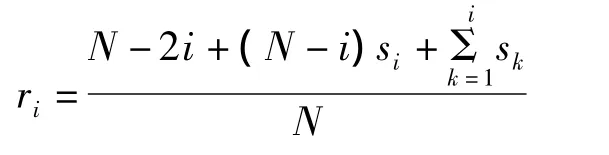
以R元素中的最小值ra作为风险值，由ra的下标变量a求出对应的阈值为附加信号的标准差.

3)Heursure阈值(启发式SURE阈值)

Heursure阈值是前两种阐值的综合，该方法所选择的是最优预测变量阈值.如果信噪比很低，则采用固定的阐值形式;若信噪比比较高时，采用启发函数自动的在前两种阈值中选择一个较小的作为阈值.

Heursure阈值的确定方法如下.

②令sure阈值T3可以表示为

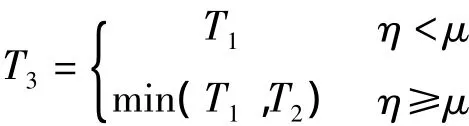
4)极大极小阈值T4(Minimaxi规则)

极小极大(Minimaxi)阈值是一种固定的阐值选择形式，它产生的是一个最小均方误差的极值，并不是无误差，它的计算公式为.

5 仿真算例

针对美国健康监测协会提出的Benchmark模型的损伤监测进行研究，结构工况选取环境激励作用每层楼，损伤工况选取一层的第24支撑发生100%损伤，噪音标准选取10%，结构模型选取12个自由度且质量对称分布，荷载激励时间为10 s，采样频率为1 000，提取结点15的加速度响应进行降噪预处理.

5.1 阈值的选取

为了选择最理想的小波去噪方案，选用前面提到的bior6.8小波函数，分解尺度为2，在对比多个阈值的情况下最终确定最优方案.在不同的情况下，评价小波去噪效果的优劣必须通过一些具体指标来衡量，采用均方根误差(RMSE)和信噪比(RSN)来衡量.

表3 不同阈值方法去噪效果比较

由以上对比可知Rigisure规则去噪效果最好，sqtwolog规则去噪效果最差，因此本文后面提到的去噪均采用Stein无偏似然估计阈值法去噪，整个去噪过程是采用Matlab中的小波工具箱［2］.

5.2 小波去噪的步骤

由于实际试验中数据量太多［3－7］，而本文只是为了说明降噪效果，所以只取结点15加速度响应的前3 s共300个数据进行Mallat2层塔式分解处理，分析中为了减小边界误差需要对边界进行对称延拓.

1)信号的分解

根据前面所述，采用bior6.8小波函数对节点15的加速度响应进行2层分解，分解后得到2层尺度系数cj，k和小波系数dj，k，见图1.

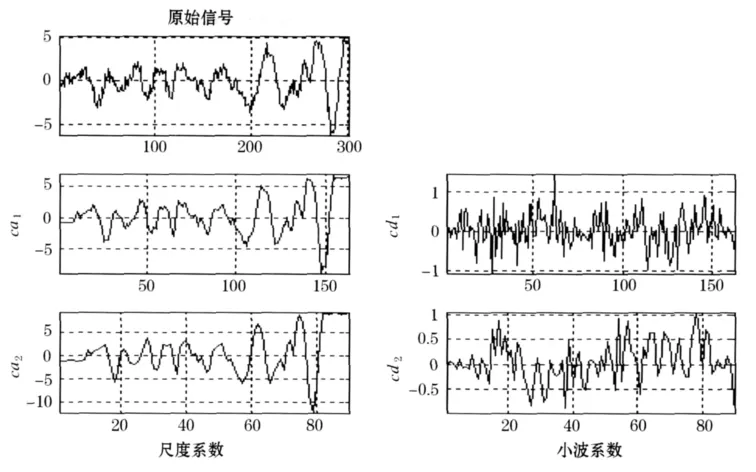
图1 2尺度bior6.8小波分解系数图

2)对小波分解得到的高频系数进行处理

对于分解得到的高频系数 d1，d2，分别采用Stein无偏似然估计阈值法进行量化处理，得到量化后的高频系数，见图2.

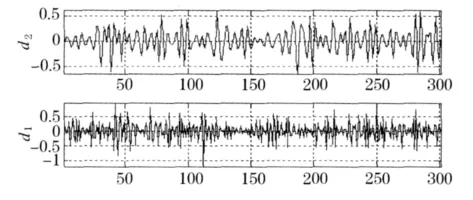
图2 2尺度bior6.8小波分解高频系数图

3)进行小波的重构

根据小波分解的第2层的低频系数和经过量化处理后的第1层到第2层的高频系数进行信号的重构，得到重构的数据，然后对对称延拓的数据进行去噪，得到最终去噪后的信号，见图3.

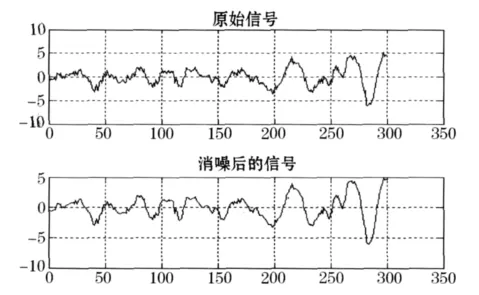
图3 去噪后的信号和原始信号对比图

从图3可以看出，经过降噪后的信号比较光滑，而且保持了原始信号的尖峰和特征，效果较好.

［1］ 文鸿雁，张正禄.非线性小波变换阈值法去噪改进［J］.测绘通报，2006(3):18－21.

［2］ 胡昌华，李国华.基于MATLAB 7.X的系统分析与设计—小波分析［M］.西安:西安电子科技大学出版社，2008.

［3］ 李爱萍，段利国.小波分析在信号降噪处理中的应用［J］.太原理工大学学报，2001，(1):69－71.

［4］ 朱 华.小波分析及其在信号降噪中的应用研究［D］.湖北:武汉理工大学，2007.

［5］ 张茁生，蔡元龙.小波分析在信号处理中的应用［J］.无线电工程，1994(8):11－18.

［6］ 文 莉，刘正士，等.小波去噪的几种方法［J］.合肥工业大学学报，2002(2):167－172.

［7］ 刘 健，范洪霞，焦艳会，等.带白噪声的小波混沌神经网络及其应用［J］.哈尔滨商业大学学报:自然科学版，2011，27 (2):177－181.