n集函数极小极大分数规划的最优性充分条件
王文君 刘红卫
(西安电子科技大学应用数学系,西安 710071)
在过去的几十年里,很多学者研究了在各种不同凸性定义下n-集函数的多目标规划的最优性理论, Lai H C和Huang T Y[1]讨论了广义(ρ,θ)不变凸性下n-集函数的极小极大规划的最优性条件,近来Preda V等[2]研究了在广义V一致不变凸性下多目标规划的重要理论.受文献[1-2]的启发,本文提出了广义type-I型的(ρ,ρ*,θ)-V不变凸函数,并在这类凸性下给出了极小极大规划的最优性充分条件.
考虑如下规划:

其中,Γn是对于给定集合X的σ代数Γ的n-折积, Fi,Gi,i∈P={1,2,…,p}和 Hj,j∈M={1,2,…, m}均是定义在Γn上的实值可微函数.对于每个i∈ P,Fi(S)≥0且Gi(S)>0,∀S∈Γn,满足Hj(S)≤0, j∈M.令X0={S∈Γn:Hj(S)≤0,j∈M}是(P)的可行集.
设(X,Γ,μ)是具有L1(X,Γ,μ)可分的有限无原子空间,Γn上的伪测度定义为

其中SkΔTk表示Sk与Tk的对称差.那么(Γn,d)是伪度量空间.对于h∈L1(X,Γ,μ)和以Iz∈L∞(X,Γ, μ)为特征函数的z∈Γ,〈h,Iz〉表示积分∫zhdμ.关于集函数的可微性是由Morris[3]首次提出来的,后经Corley[4]扩展到n-集函数上来.
定义1[4]函数F:Γn→R关于S*(,…,)的第k个分量具有偏导数,如果函数φ(Sk)=存在导数Dφ(S*k),那么定义DkF(S*)=Dφ().如果DkF(S*),k= 1,…,n都存在,那么有DF(S*)=(D1F(S*),…, DnF(S*)).
定义2[4]函数F:Γn→R在S*∈Γn是可微的,如果存在DF(S*)和ψ:Γn×Γn→R满足:


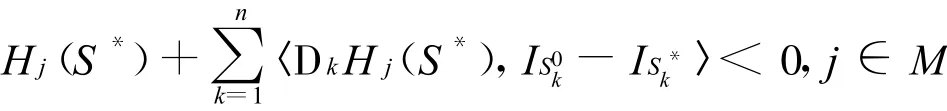
1 预备知识

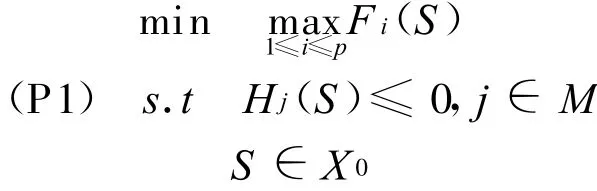
其中,函数F:Γn→Rp的分量Fi,i∈P与函数H:Γn→Rm的分量Hj,j∈M在S*处均是可微的.文献[1]给出了广义(ρ,θ)不变凸性下n-集函数,设ρ=(,下面给出的广义V不变凸的定义是对文献[1,6]的拓展.
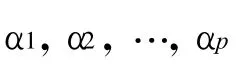
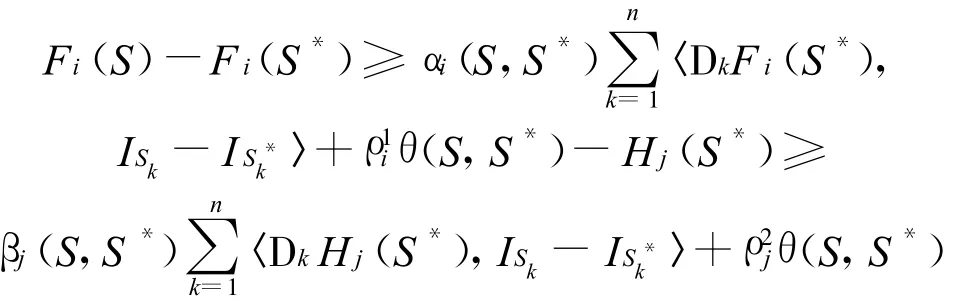
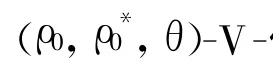
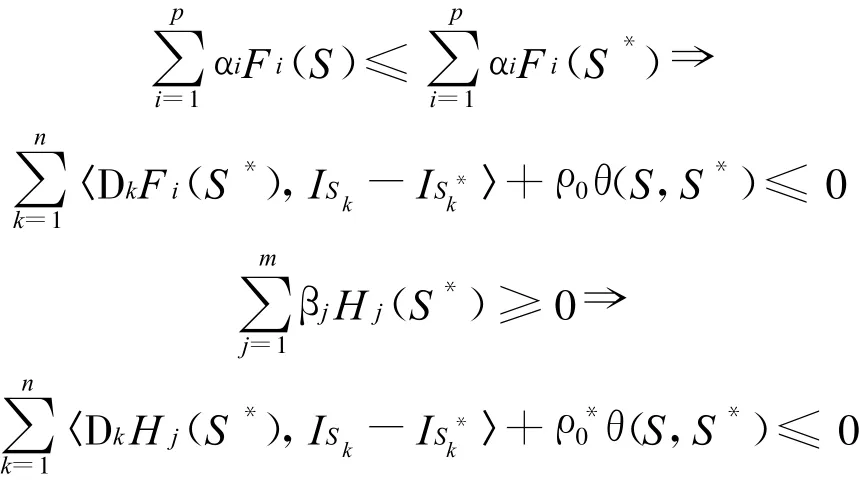
定义6 称(F,H)在S*∈Γn处是type-I型(ρ0,ρ*0,θ)-V-伪-严格拟不变凸的,如果存在定义在Γn×Γn上的正的实函数α1,α2,…,αp和β1,β2,…,βm,对∀S∈X0满足下式成立:

2 最优性条件
在本节中将给出在广义不变凸性的条件下极小极大分数规划(P)的最优性充分条件.
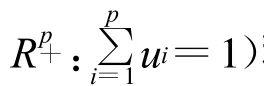

推论1[5]问题(P)的目标函数满足
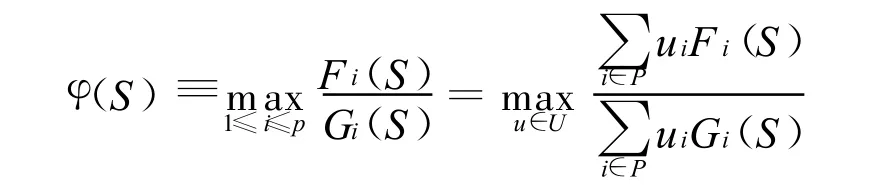

定理2(充分性) 设S*∈X0,且存在u*∈U, v*∈和λ*∈R+,对∀S∈Γn满足定理1中的式(1),(2),(3),如果
(i)[(F1(◦)-λ*G1(◦),…,(Fp(◦)-λ*Gp(◦)),(H1(◦),…,Hm(◦))]在S*处是type-I型的(ρ,ρ*,θ)-V-不变凸的;
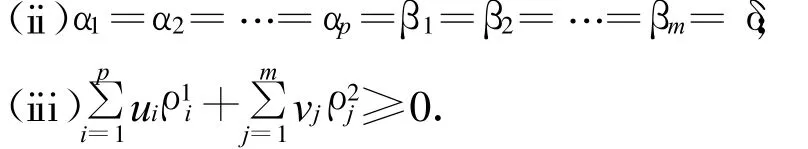
那么,S*是(P)的最优解.
证明 根据假设(i),得
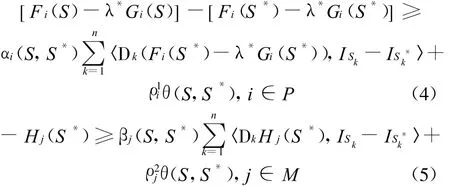
给(4)式两边乘以u*(其中u*≥0),(5)式两边乘以v*(其中v*≥0),根据式(2),(3)和假设(ii),得
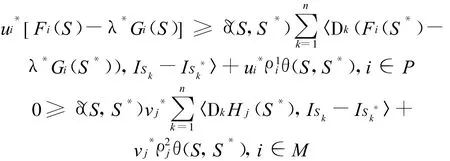
从而得知

于是得到
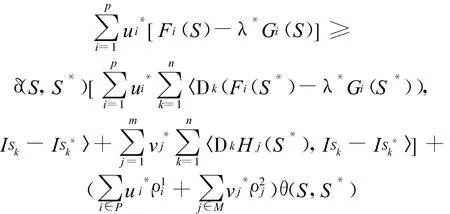
根据(1),(iii)和δ(S,S*)>0,有
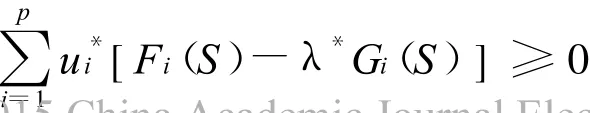
由推论1,得
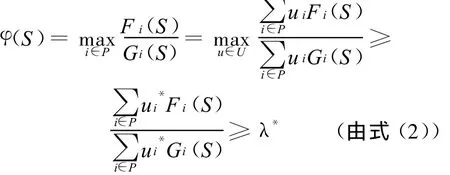
因此,S*是(P)的最优解.
定理3(充分性) 设S*∈X0,且存在u*∈U, v*∈和λ*∈R+满足式(1)和(3),如果
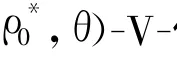
(ii)ρ0+≥0;那么,S*是(P)的最优解.
证明 假若S*不是(P)的最优解,那么存在S0∈X0满足:

由于αi(S0,S*)>0,于是有
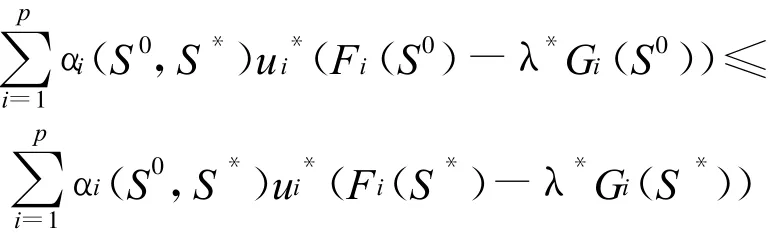
根据(i)知
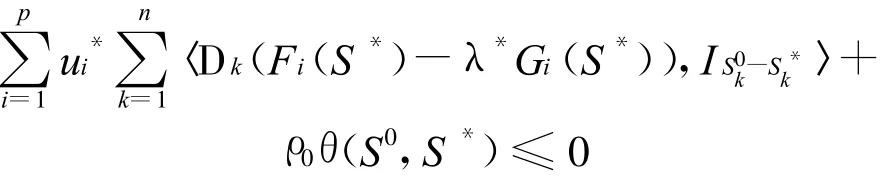
由(1)和(ii)得
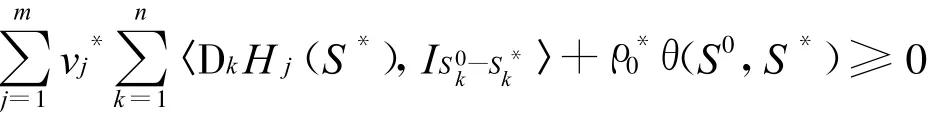
根据假设(i)知


[1] Lai H C,Huang T Y.Minimax Fractional Programming for N-set Functions and Mixed-type Duality under Generalized Invexity[J].J.Optim.Theory.Appl., 2008,139:295-313.
[2] Preda V,Stancu-Minasian I M,Miruna-Beldiman,et al. Generalized V-univexity Type-I for Multi-objective Programming with N-set Functions[J].J.Global Optim., 2009,44:131-148.
[3] Morris R J T.Optimal Constrained Selection of a Measurable Subset[J].J.Math.Anal.Appl.,1979,70:546-562.
[4] Corley H W.Optimization Theory for n-set Functions [J].J.Math.Anal.Appl.,1987,127:193-205.
[5] Zalmai G J.Optimality Conditions and Duality for Multiobjective Measurable Selection Problems with Minimax Objective Functions[J].Optimization,1989,20:377-395.
[6] Jeyakumar V,M ond B.On Generalized Convex Mathematical Programming[J].J.Austral.Math.Soc.Ser.B, 1992,34:43-53.

