基于到达角度和时间差测量的无源跟踪算法研究

乔 梁

(广东金融学院计算机系,广州 5105207)

随着信息处理和电子对抗技术的不断发展,用主动式有源辐射雷达对运动目标进行定位的方法开始暴露出极易被侦察干扰的致命弱点.因而被动定位跟踪技术受到了重视,特别是单站被动定位技术,由于具有高度独立性并且免除了复杂的时间同步装置等优点而更加引人注目[1-4].对辐射源的单站无源定位与跟踪(Single Observer Passive location and Tracking,SOPLAT)具有重要的意义和价值.

在无源定位的诸多方法中,最传统的方法是通过测量到达时间(TOA)和到达方向(DOA)来实现无机动单站对运动辐射源的快速、稳定的定位跟踪算法,这种方法具有很强的实用性.无源定位通常会涉及到非线性问题,而对非线性滤波最经典的算法是扩展卡尔曼滤波(Extended Kalman Filter,EKF).但是,在传统EKF滤波算法中,由于非线性方程的线性化舍弃了二阶以上的高次项,导致目标的跟踪精度降低.而且,EKF估计算法具有依赖于初始状态估计并受测量噪声影响大,估计过程中协方差易出现病态等缺点,导致滤波定位结果不稳定.参考文献[2-3]分别提出了将加权最小二乘估计与卡尔曼滤波相结合的无源定位方法和对机动目标无源定位IMM算法,用不同的方式研究了无源定位问题.但是概括来讲,这些方法各有自己的适用范围和局限性.文献[5]指出,如果每一个观测时刻观测器不但观测到目标辐射源相对于观测器的方位角、俯仰角,还可以通过无线电、红外或其它手段测量到它们的变化率,这时就能够对空间中的运动辐射源进行单站无源快速定位.文献[6]针对卡尔曼滤波的缺点,研究了修正增益扩展卡尔曼滤波算法.根据国内外近年来研究的启示[5-8],本文提出了一种利用辐射源时域信息和空域信息,并且采用修正增益扩展卡尔曼滤波算法对运动辐射源进行单站无源定位跟踪算法,由于它在只测向定位算法的基础上增加了方位角和俯仰角变化率信息以及时间差信息,因此它比只测向定位算法的收敛速度更快,同时还克服了EKF算法的缺欠[9-10].

1 基于TOA和DOA测量的单站无源定位原理

1.1 系统状态模型

假设辐射源辐射周期Tr恒定的脉冲信号,由于通常只能测量到目标脉冲重复周期的估计值 ＾Tr,所以需将ΔTrk=Tr-＾Tr作为未知量加入状态变量进行估计.观测站每接收N个脉冲做一次采样,则T= NTr为观测间隔.

设三维坐标条件下辐射源在k时刻的状态矢量为Xk=[xkykzk˙xk˙yk˙zkΔTrk]T,并且假设目标作一定加速度扰动下的匀速运动,观测站位于坐标原点,则可以得到辐射源的状态方程为:

1.2 系统测量模型

通常情况下无源定位观测量包括目标的方位角、俯仰角、方位角变化率、俯仰角变化率和脉冲到达时间差,这里分别称它们为空域变化量和时域变化量.根据方位角和俯仰角及其变化率、脉冲到达时间差的定义,可以得到测量方程:

式中,δβk,δεk,δ˙βk,δ˙εk,δτk分别为方位角、俯仰角、方位角变化率、俯仰角变化率及脉冲到达时间差的测量噪声.

上式可以写成矩阵形式:

1.3 线性化测量模型

由于在系统测量模型中,测量方程具有强非线性,需对其进行线性化处理.以方位角为例,将表达式在预测点 ＾Xk|k-1处进行Taylor级数展开并忽略二阶以上的高阶项,可以近似得出:

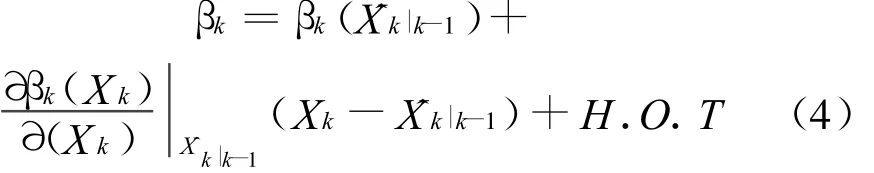
式中,

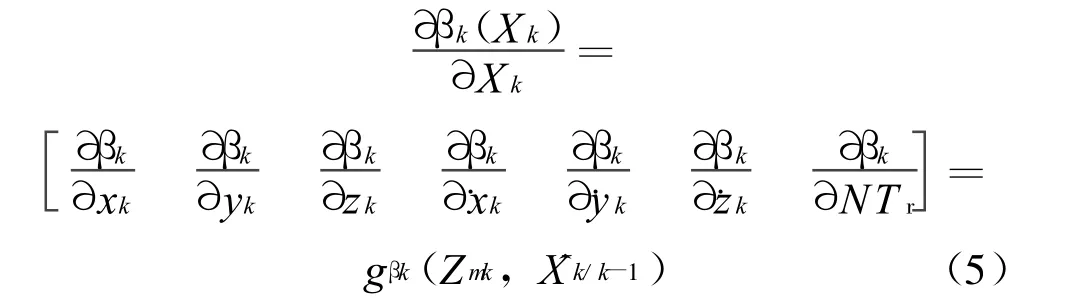
且有

同理可以对其它表达式进行线性化.

在τk测量方程中,

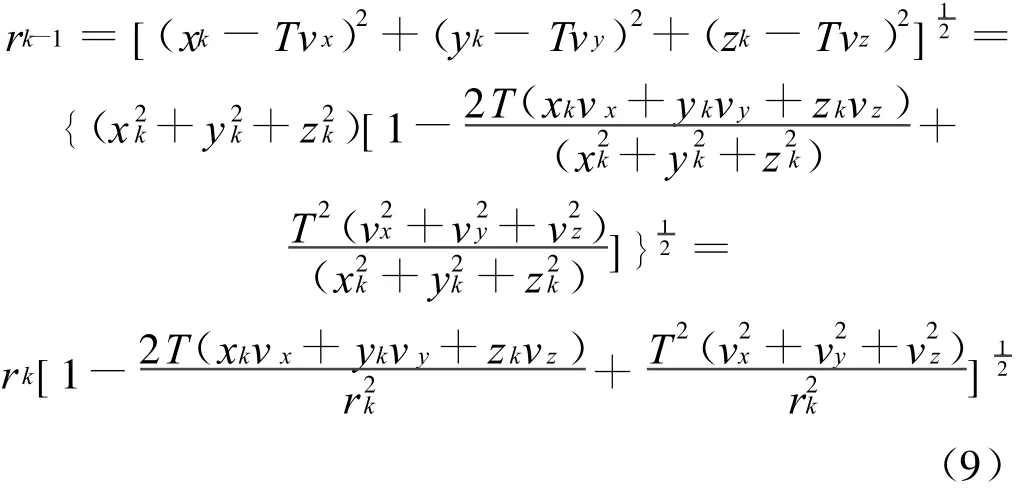
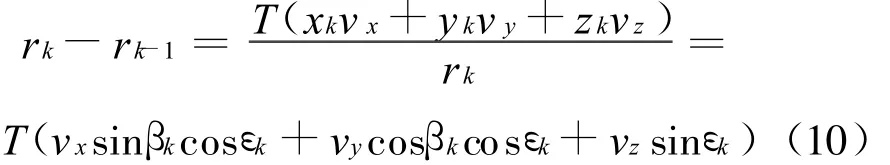
式中,

因此

所以

其中

基于TOA和DOA测量的单站无源定位原理是:经过建立测量量与目标状态之间的空间几何关系,得到系统的状态方程和测量方程,然后利用修正增益扩展卡尔曼滤波算法就可以实时得到目标状态的滤波估计值,实现对目标的定位跟踪.

2 修正增益的扩展卡尔曼滤波算法

因为EKF算法中协方差容易出现病态,以及对初始状态假定精度敏感等缺点,针对 EKF的不足, Song和Speyer提出了MGEKF(修正增益的扩展卡尔曼滤波)算法.MGEKF滤波方法在大量实践中被证明是一种对非线性系统较好的滤波算法.

应用MGEKF滤波算法的条件是非线性函数必须满足是可修正的,也就是说非线性函数h(Xk)可写成状态Xk的线性形式,即测量方程Zk=h(Xk)满足

MGEKF算法程序框图如图1所示,与EKF相比,MGEKF主要区别是用gk(Zmk,＾Xk|k-1)代替了雅克比矩阵Hk.通过MGEKF算法可以实时得到目标状态的滤波估计值.

图1 MGEKF算法程序框图

3 计算机仿真及结果分析

为验证这种定位算法的性能和有效性,对某种典型的机动目标航迹进行了计算机模拟.

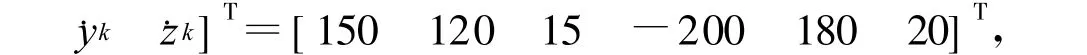
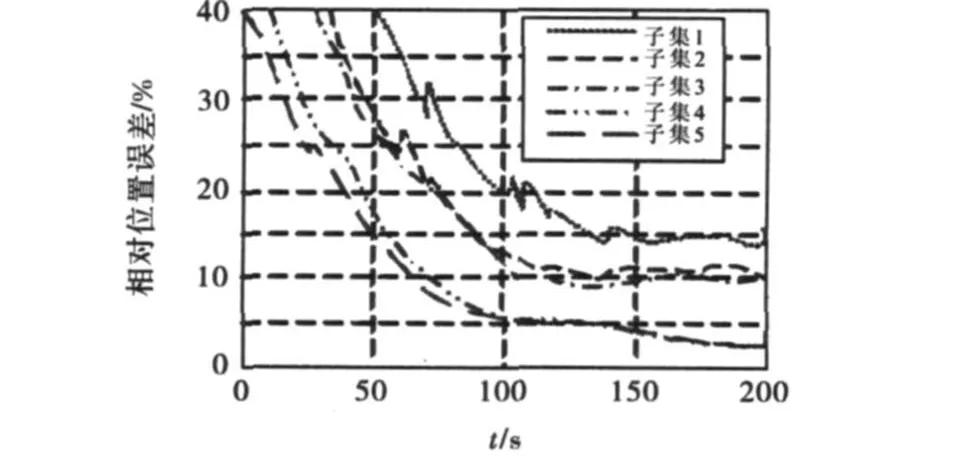
图2 相对位置误差曲线

从图2仿真结果可以得到以下结论:

(1)比较子集1和子集2可以看出,与只测角无源定位相比,加入到达时间差信息后,定位的精度和收敛速度都有了明显的提高.这一结论说明了引入到达时间差信息的有效性.

(2)通过子集2和子集3结果的比较可以看出,俯仰角变化率信息加入后对定位性能改善并不明显.比较子集4和子集5同样可以看出这一现象.产生这一结论的主要原因是,对于大多数空中运动目标而言,水平方向的速度远远大于俯仰方向的速度.所以通常情况下,单站无源定位时利用角度变化率信息可以只考虑方位角变化率.

(3)从相对位置误差曲线还可以看出,加入方位角度变化率信息的测量子集4和5的定位结果,其性能要显然优于其它子集的定位结果.这个结论说明三维定位中方位角变化率的加入可以明显加快定位收敛速度并提高定位精度.

4 结 语

本文提出的方法基于时域和空域信息,可实现对辐射体的三维定位,且只需一个接收站.随着计算机和信息处理技术的不断发展,跟踪处理器的处理速度越来越高,定位速度将会越来越快.仿真试验证明在三维条件下利用TOA和DOA信息对辐射源进行无源定位的方法是有限可行的.这种方法拓宽了被动定位跟踪技术的应用范围,使SOPLAT技术的研究走上了新台阶.尽管本文的方法还存在着一定的局限性,但仍不失为一种好的定位手段.

[1] 隋红波,王 鼎,吴 瑛.基于运动学原理的单站无源定位改进算法[J].信息工程大学学报,2008,9(1):66-69.

[2] 焦淑红,刘申建,司锡才.机动目标时差无源定位自适应滤波算法研究[J].哈尔滨工程大学学报,2001,22(5): 57-63.

[3] 王杰贵,罗景青.固定单站对机动目标无源定位IMM算法[J].信息处理,2002,18(2):137-140.

[4] 郭福成,贾兴江,皇甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析[J].航空学报,2009,30 (6):1091-1095.

[5] 郭福成,孙仲康,安 玮.对运动辐射源的单站无源伪线性定位跟踪算法[J].宇航学报,2002,23(5):28-32.

[6] 杨莘元,郑思海.基于运动辐射体TOA和DOA测量的单站被动定位算法[J].电子学报,1996,24(12):66-69.

[7] Deng Xinpu,Wang Qing,Zhong Danxing.Observability of Airborne Passive System with Phase Difference Measurements[J].Chinese Journal of Aeronautics, 2008(21):149-154.

[8] Li W C,Wei P,Xiao X C.A Robust TDOA-based Location Method and Its Performance Analysis[J].Sci China Ser F-Inf Sci,2009,52(5):876-882.

[9] 王建钢,花兴来,朱元清,等.利用波达方位角及其变化率对运动辐射源的无源定位[J].现代防御技术,2008, 36(5):119-124.

[10]王红海,朱联祥,陈 仁,等.利用GSM为信号源的无源定位系统[J].信息技术,2009(3):1-3.