一类利普希茨非线性系统的全局有限时间控制
王 康 沈艳军
(三峡大学理学院,湖北宜昌 443002)
近年来,非线性系统稳定性研究成为了研究热点,Lyapunov稳定性是非线性系统研究的重要内容之一,学者们研究各类非线性系统已得出了许多好的结果,如非线性系统的指数稳定等.然而,具有Lyapunov稳定性的系统有时在工程上的应用效果并不好,这就要求人们关注系统在有限时间内所能达到的性能要求,非线性系统的有限时间控制问题也就应运而生[1-15].所谓有限时间控制问题是指能否在有限时间内将系统控制到平衡点.
指数稳定是被控系统最快收敛速度,但此时的绝大多数闭环系统不可能在有限时间收敛到平衡点.当系统具有外部干扰和不确定因素影响时,有限时间稳定的系统往往具有更好的性能[2],因而非线性系统有限时间控制器的设计和稳定性分析更为复杂.目前,研究非线性系统有限时间控制问题的方法主要有:文献[3-4]利用齐次性理论证明齐次系统的有限时间稳定及控制器的设计,文献[5-9]利用反步构造 Lyapunov函数解决了非线性系统的有限时间控制问题,文献[10-11]利用终端滑模控制方法讨论非线性系统的有限时间控制,文献[12]利用齐次性理论解决了机器人系统的有限时间控制问题,文献[13]分别利用上述3种方法分析一类二阶非线性系统的有限时间状态反馈镇定问题.伴随着有限时间控制问题研究的深入,非线性系统的有限时间观测器设计也得到了学者的广泛关注[14-15].
本文讨论一类Lipschitz非线性系统的全局有限时间控制问题,通过所构造的一个连续非光滑的状态反馈控制器的作用,使得该系统能在有限时间内达到全局渐近稳定,并借助 Lyapunov理论,齐次性理论及系统局部有限时间稳定性理论给出了理论证明,最后,仿真结果证明了本方法的有效性.
1 预备知识
考虑如下非线性系统:

其中,f:D→Rn是连续的.

定义2[2]系统(1)的零解如果是Lyapunov稳定和有限时间收敛的,则它是有限时间稳定的.如果U=D=Rn,则它是全局有限时间稳定的.
定义3[9](齐次函数) 假设(r1,…,rn)∈Rn, ri>0,i=1,2,…,n,V:Rn→R为连续函数V被称为相对于(r1,…,rn)具有齐次自由度σ>0的函数,如果对∀ε>0,∀ξ∈Rn,使得
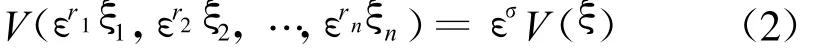
成立.


成立.
引理1[9]假设系统(1)相对于(r1,…,rn)具有齐次自由度k,则系统(1)的平衡点是有限时间稳定的,当且仅当系统(1)的原点是渐近稳定的平衡点且齐次自由度k>0.
引理2[9]假设V1和V2是在Rn连续实函数,分别相对于(r1,…,rn)具有齐次自由度l1,l2(均大于0),V1为正定的,则有,对每个x∈Rn有下式

成立.
引理3[14]假设系统存在一个定义在原点的某个领域U∈Rn内的Lyapunov函数V(x)满足
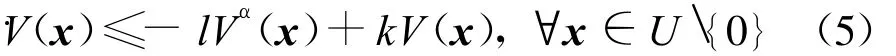
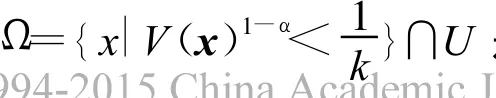
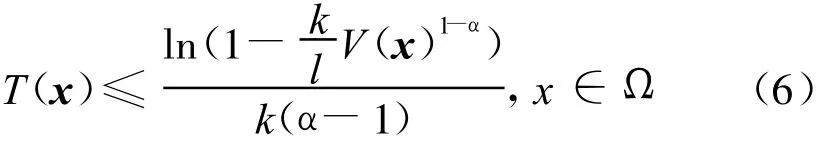
引理4 考虑以下系统

这里,x∈Rn是系统状态,hi:Rn→R是连续函数(i=1,2,…,n),若系统(7)是全局渐近稳定且原点在某邻域内是有限时间稳定的,则系统(7)的原点是全局有限时间稳定的.
引理5[16]令c,d为正实数,γ(x,y)>0为一实值函数,则有下式成立:
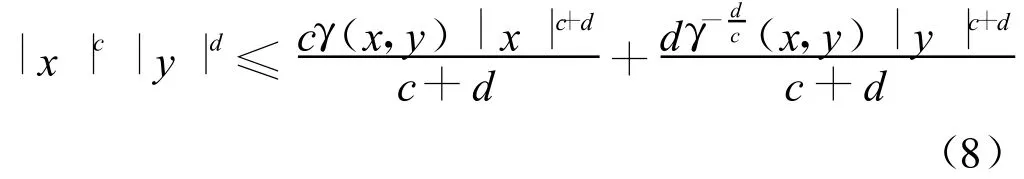
符号说明:
(1)signx为x的符号函数,其定义:当x>0时, signx=1;当x<0时,signx=-1;当x=0时,signx =0.
(2)λmax(P),λmin(P)分别表示矩阵P的最大,最小特征值.
2 主要结果
考虑以下Lipschitz非线性系统

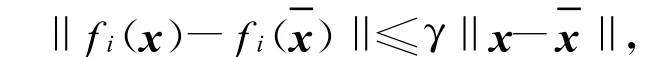

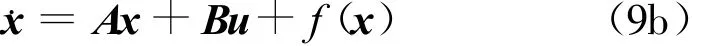
所讨论系统的全局有限时间控制问题是指系统(9)在形如以下状态反馈控制器(10)
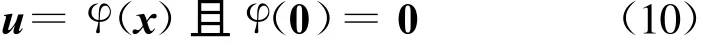
的作用下,其闭环系统

是全局有限时间稳定的.此时控制器(10)称为系统(9)的一个有限时间状态反馈控制器.
注1:文献[13]考虑了一类参数与状态不确定性非线性系统的有限时间控制问题,其非线项 fi(◦)具有下三角结构,而本文考虑的非线性项 fi(◦)与所有状态变量均有关,从而更具广泛性.
下面给出解决系统(9)的全局有限时间控制问题的主要定理.
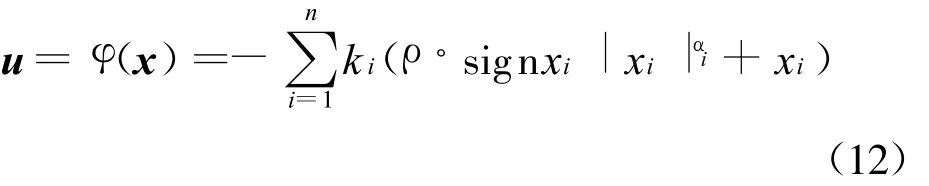
的作用下可实现闭环系统(11)是全局有限时间稳定的,其中控制器增益ki满足(k1,k2,…,kn)=BTQ,这里Q满足Riccati方程:
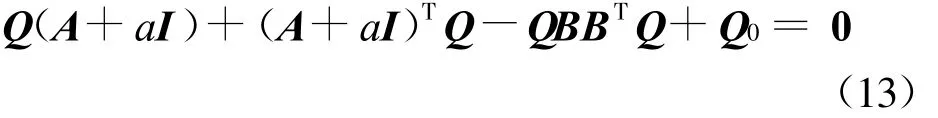
式中,a>0为适当标量,Q0为适当的对称正定矩阵, ρ,αi为控制器参数且满足
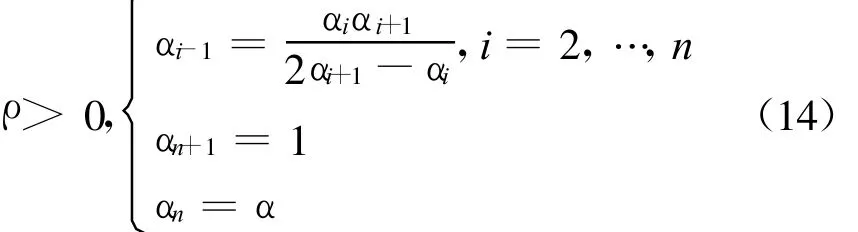
证明步骤分两步:步骤1,用 Lyapunov直接方法,证明系统(11)存在一个正定且径向无界V∈Rn,其且沿闭环系统(11)轨迹的微分在Pr=Rn-υQ(r)上是负定的;步骤2,证明闭环系统(11)在υQ(2r)上是有限时间稳定(FTS)的.由于˙V在Pr上负定且在υQ(2r)上是FTS的,意味着系统(11)是全局渐近稳定和局部FTS的,再利用引理4可完成证明.
步骤1:令系统(11)的正定Lypunov函数
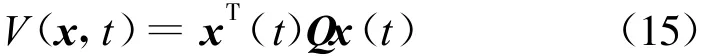
由于控制器增益ki满足(k1,k2,…,kn)=BTQ,则控制(12)可等价为
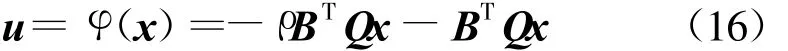
其中,x={signx1|x1|α1,signx2|x2|α2,…,signxn◦|xn|αn}.
此时,上式沿闭环系统(11)轨迹的微分为
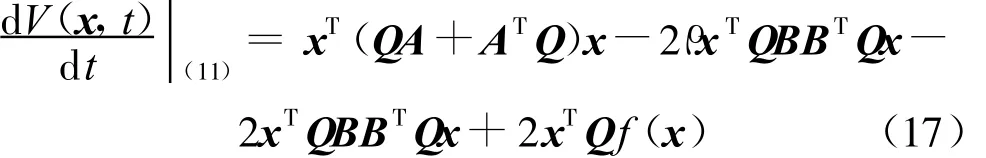
由条件(13)知:QA+ATQ+2aQ-2QBBTQ>0,将其代入式(17)可得
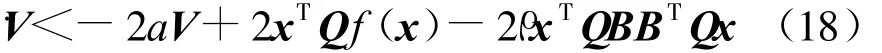
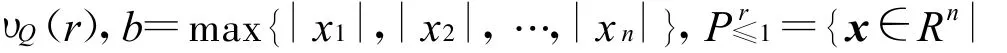
当x∈Pr≤1时,有|xi|αi≤1,i=1,2,…,n,于是有
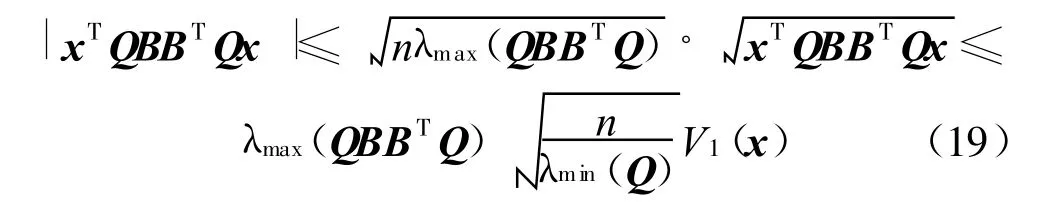
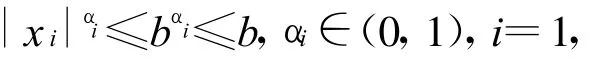
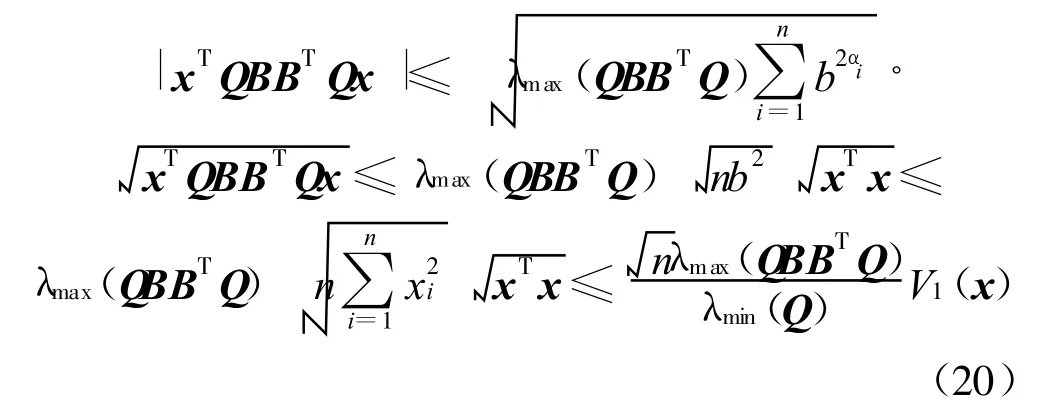
故存在

使得
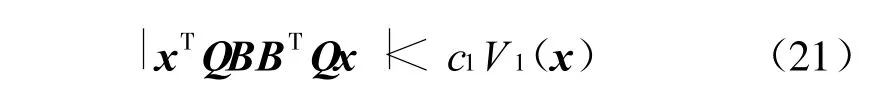

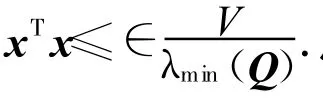


其中g(a,ρ,γ)=max{-2a+ρ c1+γ c2,-2},则有

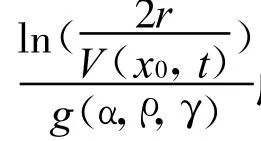
步骤2:考虑正定连续的Lyapunov函数

考虑以下系统

即

且有
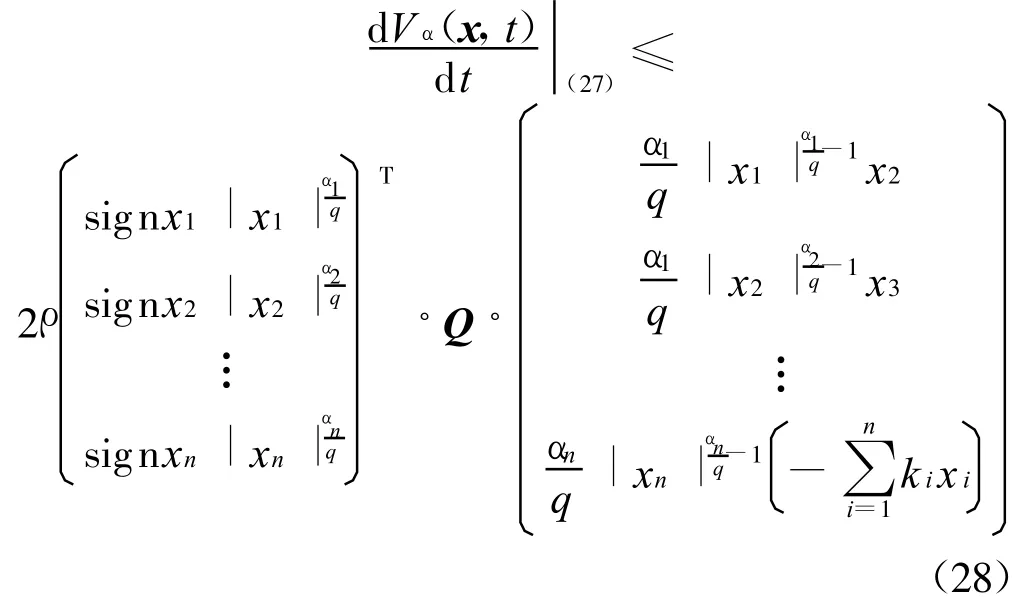
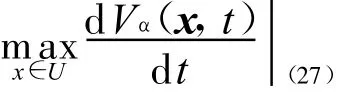

由Vα(x,t)的齐次性及引理2可知
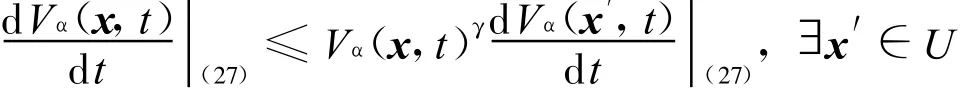
.另一方面,
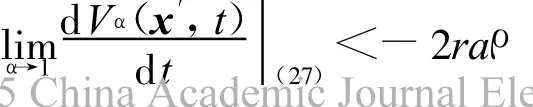
故存在ε2∈(0,1)使得对每个α∈(1-ε2,1)有

于是对∀x∈υQ(2r),存在ε2∈(0,1)使得对每个α∈(1-ε2,1)有

基于上述分析,可得正定Lyapunov函数Vα(x, t)沿闭环系统(11)轨迹的微分为


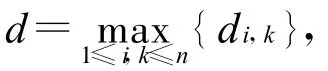
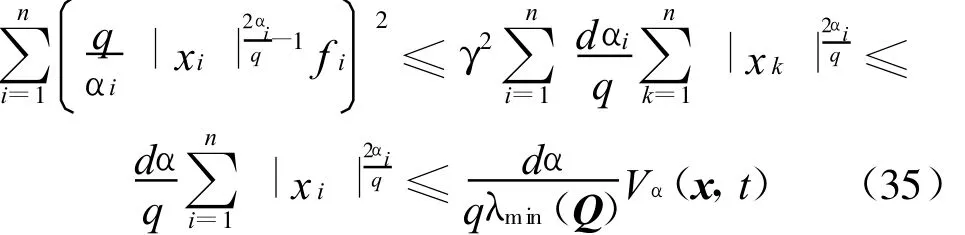
同理可得
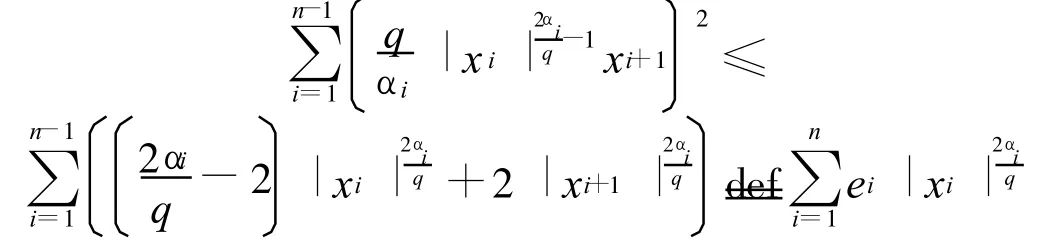
其中,ei>0,令

现要证明^xTQBBTQx的值不小于0,利用Tube引理,知道υQ(2r)是紧集,定义函数

则φ是连续的.
从而有

因此,令

则有
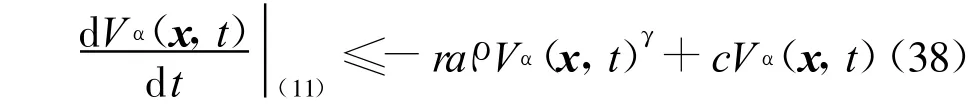
进而,由引理3和式(38)可得一个包含原点的吸引域Ω,且有υQ(2r)⊂Ω,其中
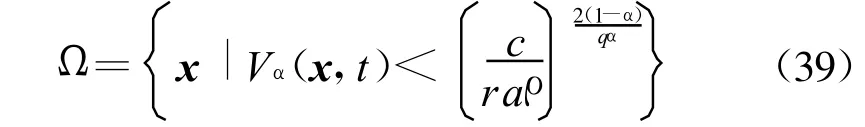
且设定时间

注2:由定理1,可按以下步骤设计系统的全局有限时间控制器(12):
(1)选定参数α,Q0,通过求解Riccati方程(13)得到Q;
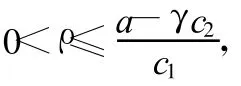
(3)设定控制器参数αi且满足条件(14);
(4)设计形如(12)的有限时间控制器.
注3:考虑系统

分析其解的情况,当x远离平衡点原点时,系统(41)可约写为˙x=-hx,此时系统是指数收敛到原点的,当x非常接近含原点的邻域时,系统(41)可约写为˙x=-jsign(x)|x|β,此时系统是有限时间稳定的,详见参考文献[12].
注4:从定理1的证明中不难得出,当α=1时,控制器(42)是控制器(12)的极限形式,且在其作用下能确保闭环系统(11)是全局渐近稳定的:

3 数值实验
考虑以下系统
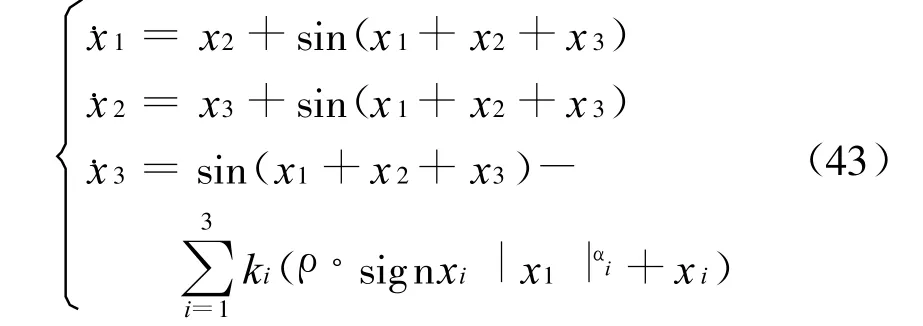


则可得有限时间控制器的增益k1=9.247 9,k2= 12.8343,k3=6.173 8,设定控制器参数为ρ=0.3, α=0.8,则可得系统状态轨迹如图1所示.
当设定控制器(12)中的参数ρ=0.3,α=1,此时的控制器是控制器(12)的极限形式,它将不再是有限时间控制器,只是一般状态反馈控制器,所得系统状态轨迹如图2所示.


由仿真实验可知,图1是系统(40)在有限时间控制器(12)作用下T=12s内就达到平衡点.图2是系统(40)在控制器(39)作用下T=20 s才被控制到平衡点.从而有力地说明了有限时间控制器比一般的状态反馈控制器具有更优的控制性能.
4 结 语
本文讨论了一类Lipschitz非线性系统的全局有限时间控制问题,设计了一个有限时间状态反馈控制器,通过Lyapunov理论,齐次系统理论和局部有限时间稳定性理论证明在其作用下的闭环系统是全局有限时间稳定的,并通过求解Riccati方程得到控制器增益,最后,通过实例仿真证明了本方法的正确性.
[1] Ryan E P.Finite-time Stabilization of Uncertain Nonlinear Planar Systems[J].Dyn.Control,1,1991:83-94.
[2] Bhat S P,Bernstein D S.Continuous Finite-time Stabilization of the Translational and Rotational Double Integrators[J].IEEE T rans.Autom.Control,1998,43 (5):678-682.
[3] Bhat S P,Bernstein D S.Finite-time Stability of Continuous Autonomous Systems[J].SIAM J.Control Optim,2000,38(3):751-766.
[4] Bhat S P,Bernstein D S.Geometric Homogeneity with Applications to Finite-time Stability[J].M ath.Control Signals Syst.,2005,17:101-127.
[5] Hong Y.Finite-time Stabilization and Stabilizability of a Class of Controllable Systems[J].Syst.Control Lett., 2002,46:231-236.
[6] Huang X,Lin W,Yang B.Global Finite-time Stabilization of a Class of Uncertain Nonlinear Systems[J].Automaica,2005,41:881-888.
[7] Hong Y,Jiang Z.Finite-time Stabilization of Non-linear Systems with Parametric and Dynamic Uncer-tainties [J].IEEE Trans,Automat,Control,2006,51(12): 1950-1956.
[8] 洪奕光,王剑魁.一类非线性系统的非光滑有限时间镇定[J].中国科学E辑,2005,35(6):663-672.
[9] Hong Y,Wang J,Cheng D.Adaptive Finite-time Control of a Class of Uncertain Nonlinear Systems[J].IEEE Trans.Autom.Control,2006,51(5):858-862.
[10]Wu Y Q,Yu X H,Man Z H.Terminal Sliding Mode Control Design forUncertain Dynamic Systems[J]. Syst.Control Lett.,1998,34(5):281-288.
[11] Feng Y,Yu X H,Man Z H.Nonsingular Terminal Sliding Mode Control of Rigid Manipulators[J].Automatic,2002,38(12):2159-2167.
[12]Hong Y,Xu Y,Huang J.Finite-time Control for Robot Manipulators[J].Syst.Control Lett.,2002,46:243-253.
[13]李世华,丁世宏,田玉平.一类二阶非线性系统的有限时间状态反馈镇定方法[J].自动化学报,2007,33(1): 101-104.
[14]Shen Y,Xia X.Semi-global Finite-time Observers for Nonlinear Systems[J].Automatica,2008,44:3152-3156.
[15]Shen Y,Huang Y.Uniformly Observable and Globally Lipschitzian Nonlinear Systems Admit Global Finitetime Observers[J].IEEE Trans,Auto mat,Control, 2009,54(11):2621-2625.
[16]Qian C,Lin W.Non-Lipschitz Continuous Stabilizer for Nonlinear Systems with Uncontrollable Unstable Linearization[J].Syst.Control Lett.,2001,42:185-200.

