滑模控制实现受噪声干扰超混沌Lorenz-Stenflo系统的同步

丰建文 代安定 徐 晨 孙少辉

(深圳大学数学与计算科学学院,深圳 518060)

混沌现象是一种非常有趣且在现实世界中普遍存在的非线性现象,自1990年Pecora和Carro[1]证明两个相同结构的混沌系统能实现同步以来,混沌同步已受到科技工作者的广泛关注,这是因为它不仅具有理论挑战性而且在保密通信、生物医学工程、化学以及信息科学等多个学科中有着重要的应用[2-6].近30年来各种新的混沌同步方法相继出现:线性与非线性反馈同步法[2]、时滞反馈控制方法[3]及自适应控制法[4]等.

在工程及其相关应用学科中,滑模控制方法是一种常用来对非线性动力系统进行控制的方法,其主要优点为对系统参数变化的敏感性、抑制外部噪声干扰性和系统的快速响应性等.滑模控制方法在使用过程中一般分为两步:第一步是为使所讨论系统得到较好的滑模运动,需选择一个适当的滑模流形;第二步设计控制器,使系统从空间中任何一点出发的轨线都能在有限时间内到达滑模流形上,且使得今后的运动一直保持在该流形上,并具有较强的鲁棒性.最近,许多研究者成功地将这种方法应用到混沌控制和同步上[7-12].但在这些工作中大多数研究对象为低维混沌系统或无噪声干扰情况下的同步问题,而对有噪声干扰的超混沌系统研究较少.然而噪声干扰在现实世界中几乎是无处不在的,并且超混沌系统由于具有两个或以上的正Lyapunov指数,其较为复杂的动力学性态使得在提高混沌保密通信系统的安全性等方面能发挥更为积极的作用,讨论受噪声干扰超混沌系统的同步问题具有重要理论意义和应用价值.

据我们所知到目前为止对超混沌Lorenz-Stenflo系统同步问题的研究工作几乎没有涉及.本文基于滑模控制理论,讨论有噪声干扰的超混沌Lorenz-Stenflo系统的同步问题,首先设计了一种被称为新型比例积分滑模流形,其次通过选择只包含一个控制项的控制器,确保在噪声干扰下滑模运动的快速收敛性和稳定性,以此来实现其同步控制.最后为了消除抖动,在滑模控制器的设计中,用陡峭的连续饱和函数来代替不连续的符号函数,提高滑模控制性能,实现对各种噪声干扰具有强的鲁棒性.

1 系统描述

超混沌Lorenz-Stenflo(LS)系统是Stenflo[13]在研究低频率短波长的重力波方程时提出来的.由下述四阶非线性微分方程描述其动力学性态

式中,x1,x2,x3,x4为状态变量,α,β,γ,r为系统参数.系统(1)是在传统的三维Lorenz混沌系统中引入了一个新的控制参数γ和一个新的状态变量x4而得到的,因而被后人称为超混沌Lorenz-Stenflo系统,且当α=1.0,β=0.7,γ=1.5,r=26.0时,系统(1)出现超混沌现象.

有噪声干扰的受控超混沌Lorenz-Stenflo系统为

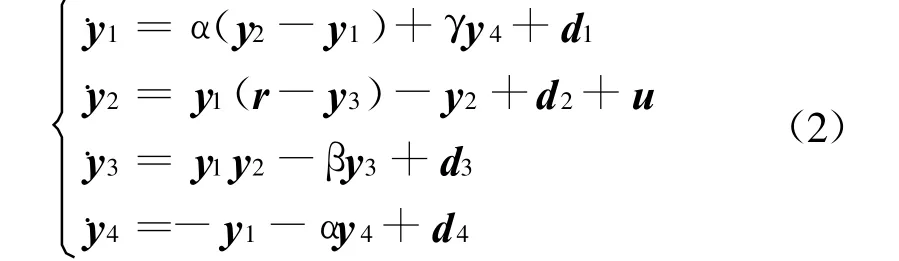
式中,d1,d3,d4为不匹配的干扰,d2为匹配的干扰[14].假设它们在C1中均为有界的,即‖di‖≤δ≤1 (i=1,2,3,4),‖di‖=supt∈R(|di(t)|+|d′i(t)|),u为控制项.

记ei=yi-xi(i=1,2,3,4)为系统误差,由(1), (2)得

2 受噪声干扰超混沌 Lorenz-Stenflo系统同步设计

首先,选取下述形式的滑模流形s=0,其中

式中,k1,k2,k3为常数.这种形式的滑模流形通常称为比例积分切换面,这样有:

定理1 若k是满足k≥δ+1的常数,控制器u定义为

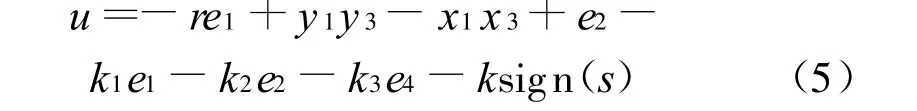
则误差系统(3)能在有限时间内到达s=0上.

证明 选取Lyapunov函数为V=s2,注意到式(4)和式(5)有

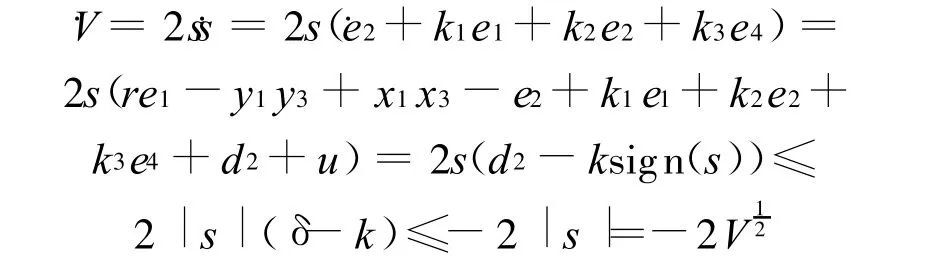
定理1表明误差系统(3)的所有轨迹在有限时间内都将达到滑模流形s=0上,为了进行同步分析只需分析误差系统在滑模流形上的动力学性态即可.在滑模流形上系统(3)为

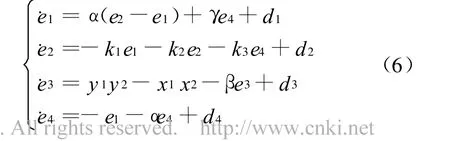
由式(6)中第1、第2和第4个方程构成关于变量e1,e2,e4的线性方程组,根据线性方程组求解理论有

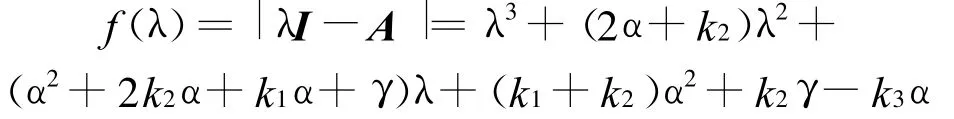
由Routh-hurwitz定理知,A的所有特征值有负实部当且仅当

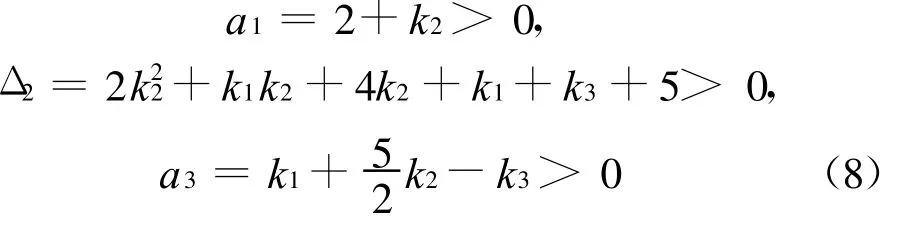
显然,使式(8)成立的k1,k2,k3存在.于是存在正常数a1和b1,成立

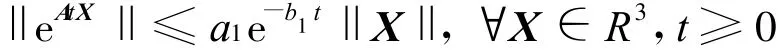
这样由式(7)得

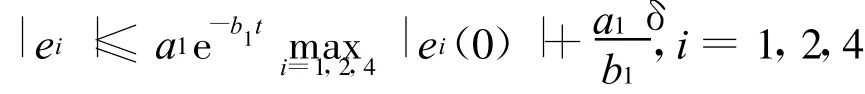
另一方面,由方程组(6)的第3个方程有

根据混沌吸引子在相空间内整体有界性,即存在M＞0,使得|x1|≤M,|x2|≤M,故

综合上面的分析可知:

定理2 若控制器u形如式(5),且k≥δ+1和k1,k2,k3满足不等式(8),则存在一个常数c1,使受噪声干扰的超混沌Lorenz-Stenflo系统(2)与超混沌系统(1)达到同步,其误差上界为c1δ,即

定理2表明,在相应的条件下受噪声干扰的超混沌Lorenz-Stenflo系统(2)与超混沌系统(1)能达到同步.但是形如(5)的滑模控制器u中含有不连续符号函数sign(s),如在理论上所讨论系统的解的存在唯一性以及Lyapunov有效性分析中对局部Lipschitz条件要求难以满足;而在实际系统中由于开关器件等的非理想性,使得滑模控制出现抖动,抖动会导致控制精度降低,电路中热功率消耗过大和机械部件磨损过快,降低系统运转性能,甚至导致系统的不稳定,最终使得系统崩溃,为此必须对控制器加以改进.

用符号函数的连续逼近是消除抖动的一种常用方法.在此用一个陡峭的饱和函数来逼近符号函数,其滑模控制器取为

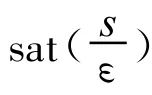
对连续控制器(9)用Lyapunov函数V=s2检验其到达滑模流形阶段的特性.由于

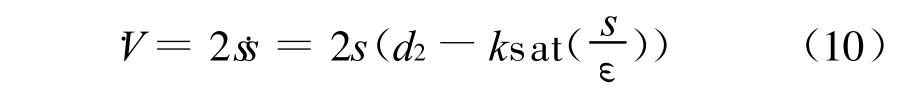
因此,在边界外层|s|＞ε,由式(10)有

上式表明,对任意的|s(0)|＞ε,|s|是严格单调递减,并会在有限时间内到达集合{|s|≤ε},其后将会一直保持在其内.称集合{|s|≤ε}为边界层.

另一方面,在边界层内有

由式(11)有

在边界层内,误差系统可化为

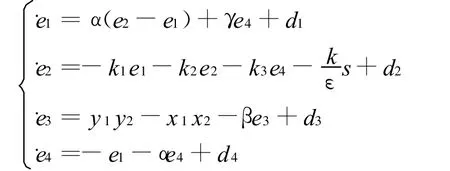
结合式(12)和定理2的证明,有

定理3 若选取控制器形如式(9),k≥δ+1且k1,k2,k3满足不等式(8),则存在一个常数c2,使受噪声干扰的超混沌Lorenz-Stenflo系统(2)与超混沌系统(1)达到同步,其误差上界为c1δ,即

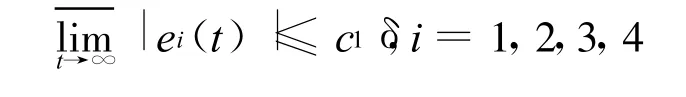
3 数值模拟

为了验证所提方法的有效性,将进行2个数值模拟实验.在实验中,驱动系统和响应系统的初始值分别取为(1,-1,3,-2)和(5,-3,2,4).选取参数k= 1.5,k1=20,k2=9.3,k3=-5.4及ε=0.001.响应系统的噪声干扰为d1=0.02cos(t),d2=0.5sin(2t),d3=0.01sin(2t),d4=0.03sin(t);数值模拟的结果如图1～2所示.图1为选用不连续控制器(5)的同步图;图2为选用连续饱和函数控制器(9)的同步图.

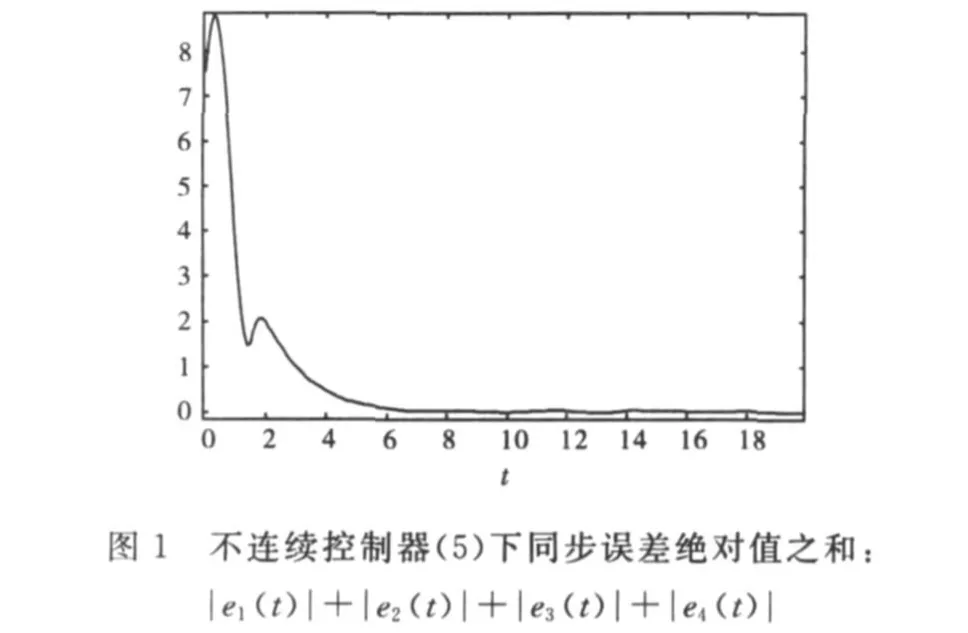
4 结 语

一般说来,对于超混沌系统的同步而言,控制项越少在实际中越容易实现.本文设计了只含一个控制项的控制器,实现了受噪声干扰的超混沌Lorenz-Stenflo系统的同步.更进一步由于控制器中含有不连续的符号函数,在实现控制过程中出现抖动.为了消除抖动,采用陡峭的连续饱和函数代替了不连续的符号函数,并运用Lyapunov稳定性理论证明了所设计的滑模控制器能实现受噪声干扰的超混沌Lorenz-Stenflo系统的同步,数值模拟的结果也证实了该方法的有效性.

[1] Pecora L M,Carroll T L.Synchronization in chaotic systems[J].Phys Rev Lett,1990,64:821.

[2] Chen G,Dong X.On feedback control of chaotic continuous-systems[J].IEEE.Trans.Circuit Syst.I,1993, 40:591-601.

[3] Song X,Yu X,Chen G,et al.Time delayed repetitive learning controlfor chaotic systems[J].Int J Bifurcation Chaos,2002,12:1057.

[4] Feng J,Chen S,Wang C.Adaptive synchronization of uncertain hyperchaotic systems based on parameter identification[J].Chaos,Solition&Fractal,2005,26:1163.

[5] Itoh M,Yang T,Chua L O.Conditions for impulsive synchronization of chaotic and hyperchaotic systems[J]. Int J Bifurcation Chaos,2001,11:551.

[6] Huang J.Adaptive synchronization between different hyperchaotic system with fully uncertain parameters[J]. Phys.Lett.A,2008,372:4799-4804.

[7] Feng J W,Xu C,Zheng W Q.Adaptive synchronization of uncertain Genesio systems based on parameter identification[J].International Journal of Nonlinear Science and Numerical Simulation,2007,8(3):419-424.

[8] Tao Y,Hui H.Synchronization chaotic dynamics with uncertainties based on a sliding mode control design[J]. physical review E,2002,65:210-217.

[9] Ming-Jyi Jang,Chieh-Li Chen,Cha'o-Kuang Chen.Sliding mode control of hyperchaos in Rōssler systems[J]. Chaos,Solitons&Fractals,2002,14:1465-1476.

[10] Yan J J,Yang Y S,Chiang T Y,et al.Robust synchronization of unified chaotic systems via sliding mode control[J].Chaos,Solitons&Fractals,2007,34:947-954.

[11]Zhang Y,Chen S H,Zhou H.Synchronizing the noiseperturbed Lü chaotic system[J].Chaos,Solitons and Fractals,2009,40:2475-2482.

[12]Feng J W,He L,Xu C,et al.Synchronizing the noiseperturbed Genesio chaotic system by sliding mode control[J].Commun Nonlinear Sci Numer Simulat,2010, 15:2546-2551.

[13] Stenflo L.Generalized Lorenz equations for acousticgravity waves in the atmosphere[J].Phys.Scr.,1996, 53:83-84.

[14]Hassan K K.Nonlinear System[M].Prentice-Hall,Englewood Cliffs,NJ,1996.