流固耦合作用下液压管道声场数值仿真
李晨阳,李维嘉,李铁成
(1.华中科技大学船舶与海洋工程学院,湖北武汉430074; 2.河南工业大学机电工程学院,河南郑州 450007)
0 引言
舰艇在航行中产生的噪声主要来自螺旋桨噪声、水动力噪声和机械噪声[1]。舰艇载流管系振动噪声是机械噪声的一个重要来源,管系振动还会传递给其他结构,并激励其产生振动噪声;管系内的噪声还会通过流体介质和管壁向水中辐射,并严重影响舰艇的隐身性能。因此,载流管系振动噪声研究具有重要意义。
载流管道声场辐射研究内容较为广泛,Jamnia[2]使用Ansys有限元软件对固液耦合作用下管道的动力响应进行了分析;Olson[3]对直管与管内流体的耦合振动的有限元法进行了综述;Pavic[4]研究了充液圆柱壳在低频振动时的4种传播波,计算并讨论了它们携带的能量流;刘忠族等[5]对管道流固耦合振动及声传播进行了综述。目前,对于管道等结构在谐响应激励下的声辐射已有较深入研究,但对于在流固耦合作用下管道瞬时分析之后,对管道进行声场时域分析较少。本文将对流固耦合作用下,直管声场的时域特性进行分析研究。以三维直管为模型,通过数值方法,探讨不同厚度的管道,不同管内流体流速对壳体噪声辐射的影响。具体的数值方法是采用Ansys有限元软件,建立管道及管内流体的三维模型,在此基础上进行耦合分析,将Ansys计算的管壁位移导入声学仿真软件Sysnoise中,从而计算流体—结构双向耦合状态下管道模型的声辐射功率级,得到管壁厚度、管内液压流速对管道声辐射的影响规律。
1 相关理论
1.1 流固耦合有限元计算方法
Wiggert提出的1组基于有限元法的输流管道流固耦合问题的离散方程:

式中:u,v,w分别为管道x,y,z三个方向位移;E为杨氏模量;Ap为管道横截面积;mp为单位长度的管道质量;ν为泊松比;p为内压;Ip为截面惯性矩;G为刚度系数;J为极惯性矩;τ为管壁剪切应力;ρw为流体密度;V为流速;D为管道内径;t为壁厚;Kf为流体体积压缩模量。
结合式(1)~式(7),并利用三维梁单元进行有限元离散化得到:

其中:[M]和[K]为管道的质量矩阵和刚度矩阵,泊松耦合由实现,结合部分耦合由{f(t)}即节点位置压力乘以横截面积实现。
1.2 结构外声场计算FEM/BEM方法
对于管壁结构存在的声固耦合作用,可以通过对模型进行单元离散,求解波动方程以及结构运动方程来实现。据文献[6]用统一的矩阵形式表示为:

式中:Ms和Ks分别为结构质量矩阵和结构刚度矩阵;Mf为流体质量矩阵;Kf为流体刚度矩阵;Q为流固耦合矩阵;Cs和Cf分别为结构阻尼矩阵和声阻尼矩阵;Fs为结构载荷向量;u和p分别为节点的位移向量和声压。对于单频声场且表面光滑的结构,Helmholtz方程可表示为:
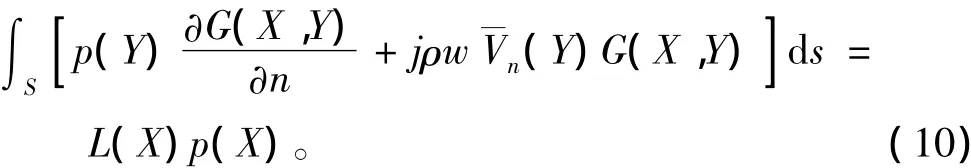
式中:X和Y分别为观测点和结构表面上的积分点,S为声源边界,X在S内部时,L(X)=0;X在S面上时,L(X)=0.5;X在S外部时,L(X)=1;p(X)为X处的声压;为自由空间的格林函数,k为波数,为法向振速;ω为圆频率。
对表面Helmholtz积分方程进行单元离散,可得边界元求解方程:

其中:[H]和[G]为系数矩阵。由此式可求得管壁表面各节点速度势,进而求得所需管道三维辐射声场。本文利用Ansys的MFX模块求解流固耦合的振动问题,可计算出管壁上节点的振动位移。通过提取节点的位移,Sysnoise程序可自动将节点位移转变成法向振速,并按式(11)计算出外壳表面压力,并可求得外部场的声学量。
2 管道流固耦合分析
对于管道流固耦合的分析计算,本文是利用Ansys中的Multi-field Solver模块实现的。该模块是Ansys 11.0中用于计算多物理场耦合问题的计算模块,在耦合计算过程中,Ansys结构计算程序和CFX流体计算程序,通过流体与结构交界面上进行力与位移的相互传递,实现流体与结构间的单向耦合或双向耦合。在Ansys中建立结构物理模型,设定流固耦合面;在Ansys中进行建立流体物理模型,并划分网格,然后将网格导入CFX-Pre进行前处理。
在考虑阀门开闭冲击的情况下,以船舶实际中常见的液压直管为模型,取管道长度L=2 m,管道内径d=0.1 m,壁厚t为输入变量,管道材料为普通钢材,密度ρp=7 800 kg/m3,弹性模量E=2.1×1011Pa,泊松比ν=0.3,忽略管道阻尼。由于管道径厚比大于10,故其所采用单元为shell63,以模拟其剪切、弯曲变形。流体为L-AN32型液油,密度ρl=900 kg/m3,温度40℃,动力粘性系数υ=25.92e-3Pa·s,流体采用fluid142单元[7],并划分为六面体网格。视管道壁为光滑壁面,计算时约束管道两端节点的径向位移。网格示意图如图1所示。

图1 网格划分示意图Fig.1Mesh of model
阀门开闭时间约为0.01 s,稳定流速V为输入变量,算例中V=4 m/s,设流速变化如下:
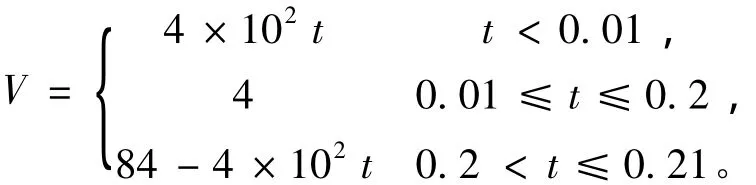
式中:流速V的单位为m/s,时间t的单位为s。
在CFX-Pro中显示的流速曲线如图2所示。
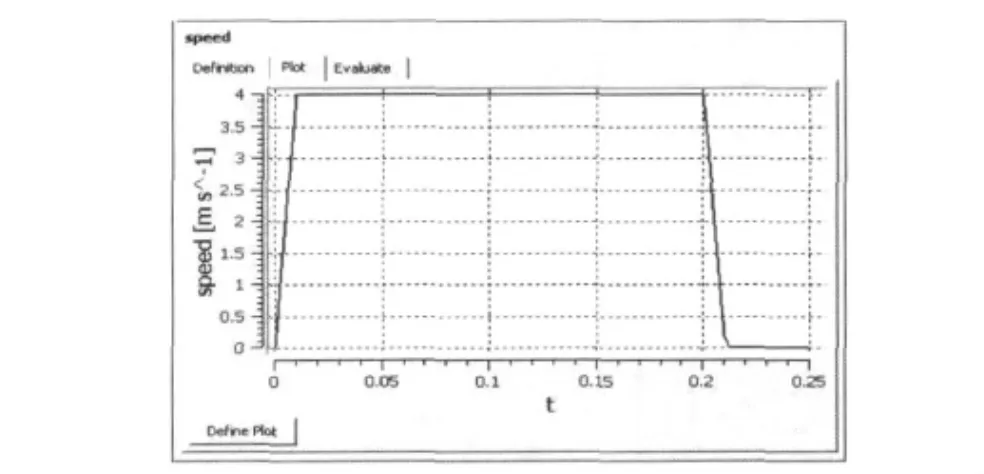
图2 流速曲线Fig.2Curve of velocity
计算分析之后,通过Ansys的POST-1中Result View可以观察在不同时刻管壁的变形位移与应力,如表1所示。
从以上液压管道仿真结果分析表明:
1)在整个仿真过程中,液压管壁的变形位移和应力均有较大的振荡,但随着入口流速变为常量,其变形位移和应力趋于稳定。在阀门关闭时,其变换又出现较大振荡;

2)在阀门开闭瞬时和入口流速变为常量瞬时,液压管管壁变形位移和应力变化较大,但在阀门开闭的过程中,其变化相对较小;

图60.100 s管壁位移云图Fig.6Displacement of pipe wall at 0.100 s
3)在整个瞬态分析中,液压管管壁最大变形位移出现的位置较为固定,在整个仿真过程中除了阀门开启瞬间入口处变形位移应力变化较大外,其余部分变化较小。
3 管壳外声场分析
管壁模型在谐响应分析后,利用Ansys与Sysnoise的接口程序[8],将Ansys中的模型文件以.cdb格式输出,并转换成Sysnoise的模型文件。提取管道外表面节点位移,转换为.fre文件,在Sysnoise中Vibrating Panels里面,将其导入作为液压管道壁的边界条件,Sysnoise内部程序自动将其转化为边界结点速度矢量。管道的物理模型与结构属性同上节所述,管道外声场流体为空气,密度ρg=1.225 kg/m3,声速c=340 m/s,参考声压取1.0×10-6Pa。

图70.007 s时xz平面声场辐射声压Fig.7Sound pressure of xz-plane at 0.007 s
由Sysnoise软件可以计算液压管管壁的辐射近场声压,在管壁附近取3个观测点:P1(0,0.06,0.05),P2(0,0.06,1)和P3(0,0.06,1.95),其声压变化如图9所示。从图中可以看出:
1)阀门开启瞬间声场辐射快速增大,在阀门开启过程中,声场波动较大,且高于稳态时声场;

2)阀门关闭瞬间声压增大,但随着激励减小,声压减小;
3)P1和P3两点曲线相似,并且明显高于P2点,是由于P2点位于管道中部,P2点所受激励小于P1和P3两点。
增大壳体厚度是一种简单且常用的降噪方法,本文对3种不同壁厚(2 mm、3 mm和4 mm)的壳体进行了仿真计算,其声辐射比较如图10所示。
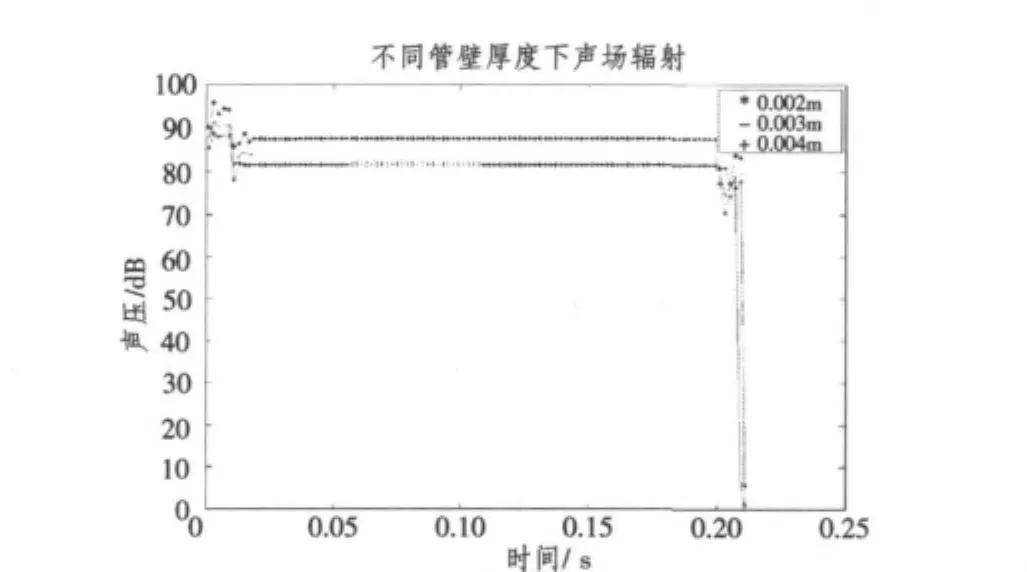
图10 不同壳体厚度的声辐射比较Fig.10Comparison of sound radiation when the thickness of shells are different
由图10可知,随着壳体厚度的增大,壳体的噪声辐射几乎在整个仿真过程中均有明显地下降,只是在阀门关闭时作用不明显。一般而言,增加管壁厚度是一种简单实用的降噪方法,但厚度增加会增加管道生产成本。因此,在选择管道时应同时考虑经济和降噪2个方面,选择合适的壁厚。
稳态流速对管壁外声场辐射也有影响,本文对3种不同稳态流速(4.0 m/s,4.25 m/s和4.5 m/s)的工况进行了仿真计算,其声辐射比较如图11所示。
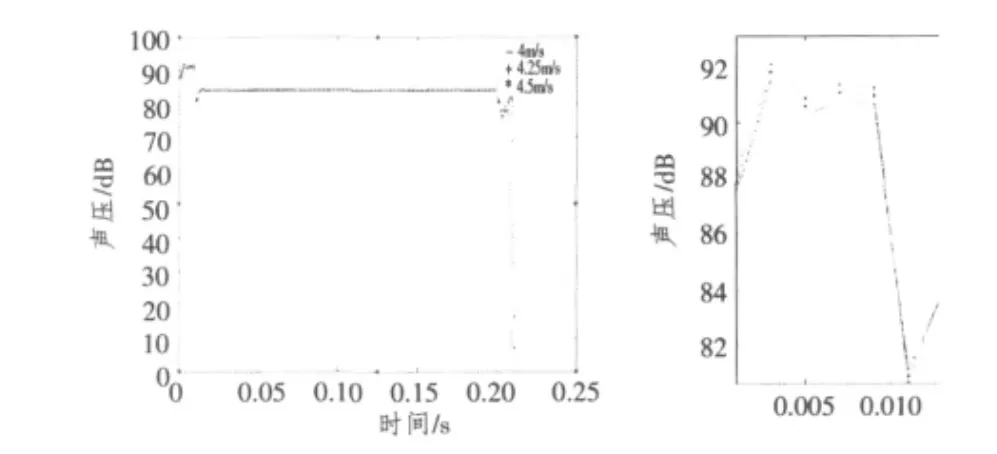
图11 不同流速下的声辐射比较(右图为阀门开启时局部放大)Fig.10Comparison of sound radiation when velocity are different(The right:the period when the valve is open is zoom in)
由图11可知,稳态流速的改变对壳体的噪声辐射影响较小,只是在阀门开启时作用较为明显。因此,缩短阀门开闭时间,在满足压力要求的情况下降低流速,对降低管壁声压有一定作用。
4 结语
在数值仿真研究中,本文初步建立了利用Ansys的MFX模块对直管液压管进行流固耦合分析,并利用FEM和BEM方法得到了管壁厚度、稳态流速与辐射声场之间的关系,结论如下:
1)利用有限元法分析流固耦合作用下的结构振动,利用边界元法计算管道外表面的声场辐射是有效的。Ansys与Sysnoise软件的相互结合为解决工程实际中液压管道振动噪声控制问题提供了可行的途径
2)增大壳体厚度,会降低壳体噪声辐射,但在设计时应综合考虑管的造价等经济因素;流速对管道声辐射影响较小,但仍应尽量降低流速;缩短阀门开闭时间可以降低声辐射。
本研究仅仅分析了在考虑流固耦合作用下,恒定稳态流速与管壁厚度对液压管道声场时域的影响情况。对阀门开闭时的出入口边界条件更为精确地描述,及其他参数改变(如结构边界约束的改变)对液压管道振动声辐射的影响效果,尚有待深入研究。
[1]姚耀中,林立.潜艇机械噪声控制技术的现状与发展[J].舰船科学技术,2006,28(S2):3-8.
YAO Yao-zhong,LIN Li.A review of control of mechanical noise for submarine[J].Ship Science and Technology,2006,28(S2):3-8.
[2]JAMNIA M A,JACKSON J E.A preliminary study for finiteelementanalysisoftwo-dimensionalfluid-solid interaction[A].In Proceedingsof the 5#International-Conference on Pressure Surges[C],BHRA,Hanover,Germany,September,1986:51-62.
[3]OLSON L G,JAMISOND.Applicationofageneral purpose finite element method to elastic pipes conveyingfluid[J].J.Fluids&Structures,1997,11:207-222.
[4]PAVIC G.Vibration energy flow in elastic circularcylindrical shells[J].Journal of Sound and Vibration,1990,142(2):293-310.
[5]刘忠族,孙玉东,吴有生.管道流固耦合振动及声传播的研究现状及展望[J].船舶力学,2001,5(2):82-90.
LIU Zhong-zu,SUN Yu-dong,WU You-sheng.Current situation and trends on the study of coupled fluid-structure vibration and soundpropagation of pipeline systems[J].Jornal of Ship Mechanics,2001,5(2):82-90.
[6]王勛成.有限单元法[M].北京:清华大学出版社,2003.
WANG Xu-cheng.Finite Element Method[M].Beijing: Tsinghua University Press,2003.
[7]Ansys Inc.Ansys 11.0 help[Z].2006.
[8]王晶,商德江.Ansys和Sysnoise之间的数据接口技术研究[J].应用科技.2004,31(8):32-34.
WANG Jing,SHANG De-jiang.Study of the interface between Ansys and Sysnoise[J].Applied Science and Technology,31(8):32-34.

