弹性障板下水声基阵辐射声场计算

张俊，陈亚林，吕林夏

（1．中国船舶重工集团公司第七○五研究所，陕西西安710075; 2．水下信息与控制重点实验室，陕西西安 710075）

0 引言

在声辐射计算领域，比较成熟的数值方法是有限元法和边界元法。有限元法在水声领域的应用主要是水声换能器的设计和分析，能很准确地计算出换能器的谐振频率，导纳曲线发射指向性图等。其在压电、结构、声学耦合分析方面的准确性已经得到了验证。但是在声辐射计算方面，有限元法也存在不足。主要表现在:一是计算量比较大，对计算机的要求比较高;二是对于工程中常见的无限外空间声辐射问题，有限元法不能有效地模拟截止边界，从而导致计算误差比较大。边界元方法是由Helmholtz边界积分方程并且结合边界元的离散技术发展起来的一种数值计算方法。它把问题的求解维数降低一维，并且把解析解和数值解相结合，具有较小的计算量和较高的计算精度。同时边界元法适合于无限域的声学计算问题，这弥补了有限元法在这方面的不足。

在声学基阵声辐射方面，Audoly［1］和Yokoyama［2］分别利用改进的Helmholtz边界积分方程计算了有限大障板上平面基阵的辐射声场。何正耀［3］用边界元软件Sysnoise计算了刚性障板条件下共形阵的辐射声场，得到了阵元间的互辐射阻抗和基阵的远场指向性。但是他们分析计算的都是在刚性障板下的基阵声辐射问题。对于有限大的弹性障板的特性，只采用边界元法无法实现计算目的。本文利用有限元法在结构模态分析上的准确性和边界元法在处理无限域声辐射问题上的优势，采用有限元和边界元相结合的方法，建立弹性障板下平面基阵的结构边界元模型，对其远场指向性进行计算，并且对比分析弹性、柔性和刚性障板对整个基阵远场指向特性的影响。为工程中基阵的工程设计提供指导。

1 理论模型

1.1 声学有限元理论模型

均匀的理想流体中三维波动方程为［3］:

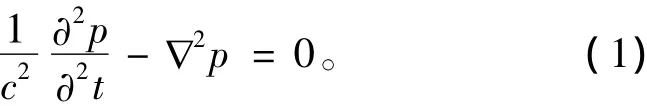
用有限元方法对声波方程进行离散，同时考虑流固耦合处能量的损耗，得到离散化的有限元声波方程:

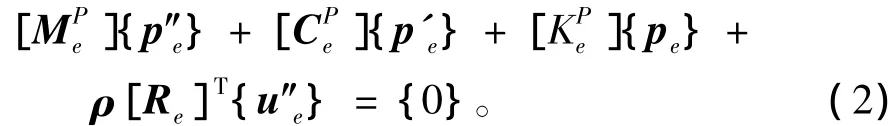
式（3）与式（2）相结合，就得到完整的求解声学问题的流固耦合控制方程为:

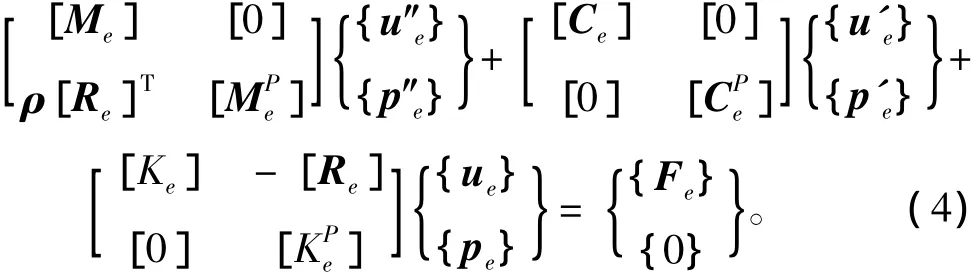
1.2 声学边界元理论模型

对于简谐波声压为正弦时间函数，设波动频率为ω，则声压p可以设为

代入三维波动方程式（1）中，得到:

在一个由封闭表面S所围成的体积V中，对于2个在S上和V中都有一阶和二阶连续有界偏导数的函数φ和ψ。根据格林公式可以把体积分转化为面积分:

式（7）是格林第二积分方程，它可以用来解决三维空间的声辐射问题。如果振动体的体积为V，表面积为S，设格林公式中的φ和ψ分别为:

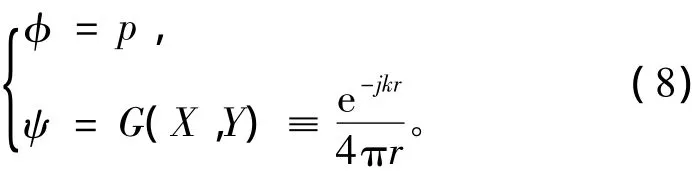
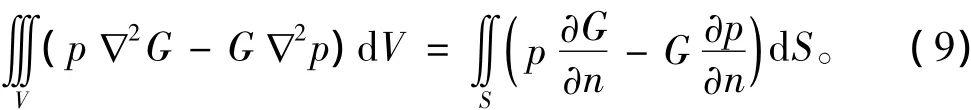
结合式（6）和式（9），考虑场点在体积V内部、表面S上和外部3种情形，并且假设辐射表面光滑，可以推导出开放空间内声辐射问题的赫姆霍茨边界积分方程:

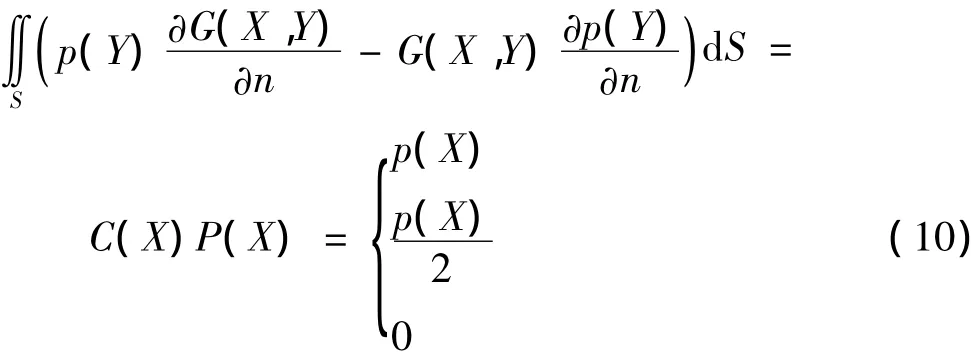
当场点X在辐射体外部时，C（X）=1;当场点X在辐射体表面时，C（X）=1/2;当场点X在辐射体内部时，C（X）=0。

本文应用当前国际上流行的有限元软件Ansys和边界元声学软件Sysnoise联合建立弹性障板下平面基阵的结构边界元声学混合模型。首先用Ansys软件对声学结构进行精确的网格划分和准确地模态分析，然后在SysnoiseE软件中，利用Ansys软件建立的网格模型和模态参数建立结构边界元计算模型，计算弹性障板下平面基阵的水平轴面内的声压分布和远场指向性。

2 计算实例

2.1 圆柱形弹性障板下37元平面阵声场计算

建立37个阵元的平面阵模型，阵元位置排列如图1所示。阵元辐射表面为正方形薄板，边长a=3 cm，厚度b=0.3 cm，阵元垂直和水平间距相同。障板为一圆柱壳，障板高h=20 cm，底面半径R=13 cm，壳体厚度D=0.5 cm。阵元材料为硬铝，密度ρ=2 700 kg/m3，杨氏模量E=6.85×1010N/m2，泊松比σ=0.34，声速c=6 260 m/s;障板材料为玻璃钢，密度ρ=1 750 kg/m3，杨氏模量E=1.8×1010N/m2，泊松比σ=0.14，声速c=2 510 m/s。障板阻抗ρc= 4 392 500 Pa·s/m，与水的阻抗可以相比拟，可以看成是弹性障板。

图1 基阵边界元模型Fig.1The BEM model of arrays

建立基阵的几何模型，用有限元法进行网格划分，对基阵进行结构模态计算，频率f范围为10～30 kHz。共得到526个结构模态。表1为f=20 kHz前后的10个模态。

把有限元网格模型和模态参数分别保存为网格数据文件和Ansys文件。首先把网格数据文件导入到边界元软件Sysnoise中建立间接边界元模型，如图1所示。然后把保存模态参数的Ansys文件导入到软件中，软件会自动生成间接边界元和结构有限元耦合模型。节点振速设为v=1 m/s，设置障板和阵元的材料参数。计算得到频率f=20 kHz时基阵的0°方向上远场指向性分别如图2中所示，实线为Sysnoise计算值，虚线是由平面波模型计算所得到的理论值。图3为当频率f=20 kHz时，主波束在0°方向时轴平面上的声压分布图，所显示平面区域长宽均为2 m。

由结果可知，－3 dB带宽为19.03°，旁瓣级为21.34 dB。由图中可以看出，这与理论值是比较接近的。由于障板的弹性特性和网格划分不对称的影响，由Sysnoise所计算的基阵远场指向性左右旁瓣已经不具有理想的对称性，特别是接近障板边缘处的旁瓣已经表现的比较凌乱，与理论值相差比较大。从声压分布图中可以看出近场处声波的衍射现象比较严重。

2.2 不同阻抗障板下37元阵远场辐射指向性对比

在水声场中，当障板的声阻抗分别远小于、远大于水的声阻抗或者与水的声阻抗相当时，就可以分别看成是柔性、刚性和弹性障板。它们分别对应着声学中的绝对软、绝对硬和混合边界条件。有如下的特性:

1）柔性障板，这时障板边界上的声压为0，即p（x，y，z，t）=0。其物理意义为界面上的任何点上，不论时间t取何值，声压p总为0。

2）刚性障板，声波不能进入该介质中，此时边界上介质质点的法向振速应为0。用数学模型表达为

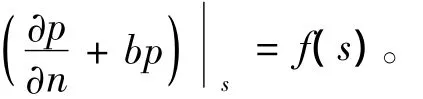
式中:系数a，b均为常数;s为边界。当f（s）=0时，则称其为阻抗边界条件。

建立37元平面阵及障板模型，几何参数与上一小节所建立的模型一致。障板材料阻抗属性分别设置为柔性、刚性和弹性。根据上面3种情况，对于柔性障板和刚性障板，选用间接边界元（DBEM）计算模型，分别设置障板节点声压为0和节点法向振速为0;对于弹性障板模型，同样选用玻璃钢，采用结构有限元和边界元混合计算的方法。计算频率为归一化频率f=15 kHz。图4和图5分别为束控方向0°时，3种障板下的远场指向性图。是表示界面沿外法线方向的偏导数。

3）弹性障板，在界面上声压和振速是线性组合关系，其数学表达式为

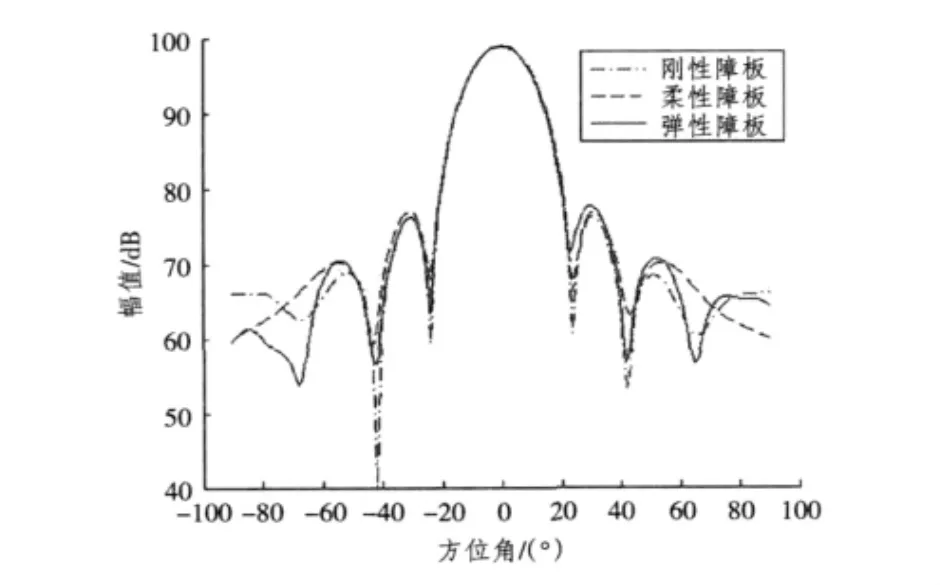
图4 0°束控时基阵水平远场发射指向性图Fig.4The far-field directivity of arrays when 0°beam control

由图6可以看出，当主波束束控在0°角上时，柔性、刚性、弹性3种障板下，基阵的主波束吻合的非常好，第一旁瓣也基本一致，第二、三旁瓣有差异。这说明不同材料障板对基阵的影响主要集中在靠近障板边缘处。当主波束束控在30°和45°时，刚性障板和柔性障板下基阵远场指向性趋势一致。但是弹性障板下基阵的主瓣和旁瓣都有较大的改变，30°和45°束控时均在－20°方向出现了较高的旁瓣。30°束控时主瓣宽度较之刚性和柔性障板条件下变小，45°束控时第一旁瓣已经不明显，主瓣下端变胖。

3 结语

1）本文通过边界元和有限元相结合的数值方法计算了弹性障板下水声基阵的辐射远场指向性和近场声压分布，所得结果与解析解相吻合。但是解析解不能很好地考虑障板条件对基阵的影响，特别是复杂的障板条件下基阵的声场计算问题，数值方法比解析方法有明显的优势。

2）由结果可以看出，障板对基阵辐射声场的影响主要体现在对其远场指向性旁瓣的影响和对其近场声场的影响。越接近障板边缘，旁瓣的变形越大。在近场处，声波的衍射现象也比较严重。特别是弹性障板条件下，这种影响更为严重，特别是做波束偏移时，主瓣和旁瓣都有比较明显的改变。这一点，在基阵的设计时值得考虑。

3）边界元声学数值方法中，模型网格的划分质量对结果也有明显的影响。对于本文中建立的圆柱体弹性障板，网格单元的分布不对称，对其远场指向性旁瓣也有一定的影响。优化网格划分，进行精确快速的建模和计算是有待进一步开展的工作。

4）本文所用到的分析方法不只适用于平面阵，对于阵元排列和障板结构更为复杂的体积阵也同样可以适用。这比平面波理论模型更接近工程实际，为声呐基阵的工程设计，特别是在多种材料混合使用下基阵设计提供了一种预报基阵声学性能的数值方法。

［1］CHRISTIAN A．Some aspedts of acoustic interactions in sonar transducer arrays［J］．J．Acoust．Soc．Am．1991，89 （3）:1428－1433．

［2］YOKOYAMA T，HENMI M．Effects of mutual interactions on a phased transducer array［J］．Jpn．J．Appl．phys．，1998，38（5）:3356－3360．

［3］SYSNOISE Rev 5.5 Manuals［M］．LMS Company，2005．

［4］杜功焕．声学基础［M］．南京:南京大学出版社，2001．

DU Gong-huan．The Foundation of Acoustics［M］．Nanjing: Nanjing University Press，2001．

［5］周福洪．水声换能器及基阵［M］．北京:国防工业出版社，1984．

ZHOU Hong-fu．Underwater Acoustics Transducer and Arrays［M］．Beijing:National Defence Industry Press，1984．

［6］MOAVENI S．有限元分析［M］．北京:电子工业出版社，2008．

MOAVENI S．Finiteelementanalysis［M］．Beijing: Electronic Industy Press，2008．

［7］何祚镛．结构振动与声辐射［M］．哈尔滨:哈尔滨工程大学出版社，2001．

HE Zuo-yong．Structure Vibration and Sound Radiation［M］．Harbin:Harbin Engineering University Press，2001．

［8］CISKOWSKI R D，BREBBIA C A．Boundary Element MethodsinAcoustics［M］．SouthamptonBoston Computational Mechanics Publications，1991．

［9］COPLEY L G．Integral equation method for radiation from vibrating bodies［J］．Journal of the Acoustical Society of America，1967，41（4）:807－816．