基于 ADAMS/Vibration的曲轴受迫振动分析

马淑英,陈立东,刘荣昌,陈建伟

(河北科技师范学院机电工程学院,河北秦皇岛,066600)

曲轴系统作为发动机上主要的运动部件,它的性能优劣直接关系到发动机乃至整车的性能、可靠性和寿命。曲轴系的振动是引发内燃机振动的主要因素。曲轴上作用有大小、方向周期性变化的切向和法向作用力,故曲轴会产生扭转振动[1]。由于曲轴较长,扭转刚度较小,且曲轴系的转动惯量较大,故曲轴扭转振动频率较低,在发动机工作转速范围内容易产生共振,从而引起较大噪声、加剧其它零件的磨损,甚至导致曲轴折断。曲轴的振动本质上是三维形式的振动,不仅扭转振动是人们研究的主要内容之一,弯曲振动、纵向振动也成为研究的重要内容[2]。因此,开展轴系多维振动的机理与控制方法的研究既有较高的学术价值,又有明确的工程应用意义。

1 曲轴的振动分析方法

由于曲轴的结构和受力情况都比较复杂,在计算曲轴轴系的振动特性时,一般都要将轴系简化为比较简单的力学模型,以便于求解。早期的曲轴振动研究主要采用离散化方法,并将曲轴振动作为纯扭转振动处理。目前,多采用 Holzer法、传递矩阵法、有限元法、弹性波法、模态分析法等曲轴振动分析方法,其中传递矩阵法因计算方便快速应用最广,有限元法因计算精度高而受人青睐,弹性波传播法兼具上述两种方法的特点,开始被引入曲轴振动计算[3]。

2 ADAMS软件简介

ADAMS软件是美国 MDI公司(Mechanical Dynamics Inc.)开发的虚拟样机分析软件,它由基本模块、扩展模块、接口模块、专业领域模块及工具箱 5类模块组成。用户不仅可以采用通用模块对一般的机械系统进行仿真,而且可以采用专用模块针对特定工业应用领域的问题进行快速有效的建模与仿真分析[4]。

3 曲轴系受迫振动分析

3.1 刚柔耦合曲轴系模型的建立

多柔体系统不同于刚体系统,当多柔体系统中体的弹性不可忽略时,在多体系统的建模和分析当中必须将体的柔性变形考虑进来,考虑部件柔性的多体系统称为柔性多体系统[5]。多柔体系统动力学是多学科交叉发展的产物,所研究的问题包括了宏观世界机械运动的主要问题,研究可变形体和刚体组成的系统在经历大范围空间运动时的动力学行为[6]。多柔体系统动力学不仅考虑将系统中子部件有些抽象为刚体,计算铰接处的弹性和阻尼,而且考虑部件的变形,它相比多刚体动力学更侧重于研究部件的变形与运动的相互耦合作用所产生的动力学效应。柔体模型的建立方法主要有离散化方法和模态集成法。

3.1.1 模态集成法 模态集成法的基本原理是将柔性体视为有限元模型的节点的集合,相对于局部坐标系有小的线性变形,而此局部坐标系做大的非线性整体平动和转动[7]。每个节点的线性局部运动近似为模态振型或模态振型向量的线性叠加。如果局部坐标系的位置用它在惯性参考系中的笛卡尔坐标X=(x,y,z)和反映方位的欧拉角 ψ=(ψ,θ,φ)来表示,模态坐标用 q={q1,q2……qm}T(m为模态坐标数)来表示,则柔性体的广义坐标可选为:

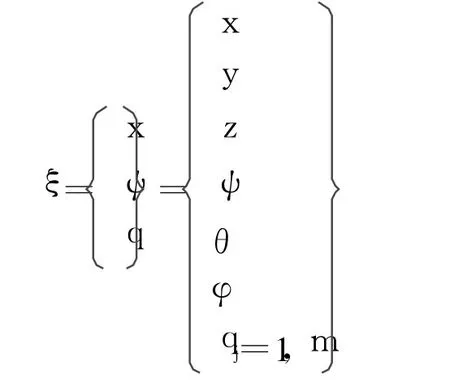
式中,x,y和 z是局部坐标系相对于整体坐标系的空间位置;ψ,θ和 φ是局部坐标系相对于整体坐标系原点的欧拉角;qj是第 m阶模态振幅的振型分量。

柔性体第 i个节点的空间位置矢量确定为:

式中,X表示局部坐标系在惯性坐标中的空间位置矢量;A表示局部坐标系相对于惯性坐标系原点的方向余弦矩阵;si表示第 i个节点未变形前在局部坐标系的空间位置矢量;φi表示第 i个节点的移动自由度的模态矩阵子块;q表示模态振幅向量。将式(1)对时间求导,得到第 i个节点的速度为:

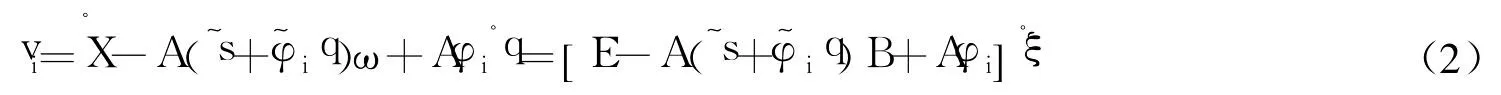
式中,ω表示局部坐标系的角速度向量;B表示将欧拉角对时间求一阶导数变为角速度的转换矩阵;“└”表示向量对应的对称矩阵;φ′表示第 i个节点的转动自由度的模态矩阵子块。节点 i的角速度也可以用物体的刚体角速度与变形角速度之和来表示:ωi=ω+φ′·q。 从上式可以得到动能和势能的表达式如下:

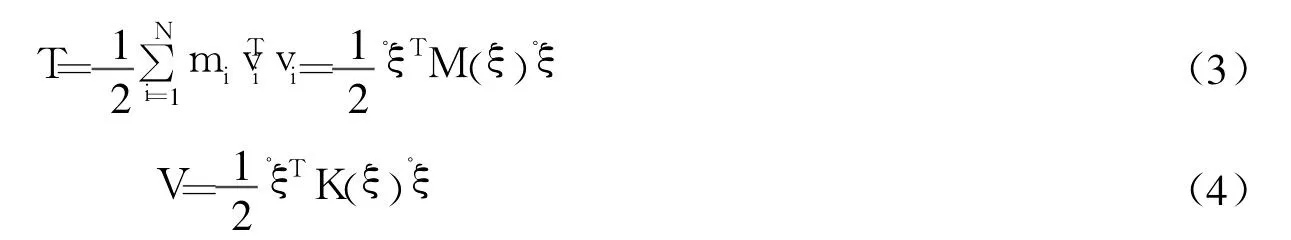
将上式代入拉格朗日方程,就可得到 Adams的柔性体方程式如下:

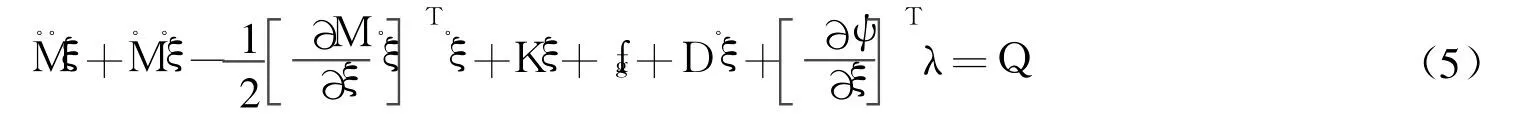
在此柔性体方程式中,K和 D分别为柔性体的模态刚度和阻尼矩阵,刚度和阻尼的变化只取决于变形。因此,刚体的平动和转动对变形能和能量损失没有影响。重力写成 fg。λ为约束方程的拉格朗日乘子,ψ和 Q为外部施加的载荷。对柔性体方程的求解,首先采用 Newton-Raphson算法迭代将其展开。展开中产生的稀疏矩阵,采用吉尔 Gear刚性积分方法可以实现高效求解。方程式(5)中的质量矩阵是变形和方向的复杂函数,但通过确定 9个惯性常量,计算速度将会有很大提高。

3.1.2 集成有限元模型的多体理论分析 在有限元分析中,分析对象划分的网格节点,是相对于对象本身的某一惯性坐标。为了描述方便,一般将惯性坐标固定连在物体的一端,并将坐标的一个轴线与物体的轴线重合[9]。将有限元分析的柔体加入多体系统中,需将柔体作相对的位移,即需将柔体分析的有限元方程乘以转换矩阵,从而实现由局部坐标向整个模型的惯性坐标的转换。

采用拉格朗日方法建立的多体系统动力学,当代入其各项因子后,其简化形式如有限元方程:

式中,M=BmeBT,me为静止状态下的单元质量矩阵;C=BceBT,ce为静止状态下的单元阻尼矩阵;K=BkeBT,ke为静止状态下的单元刚度矩阵。有限元模型的通用结构分析方程,一般是在有限元分析对象的局部坐标系下建立的。方程中的变量是相对于局部坐标的坐标元素。为了实现有限元分析方程与多体系统动力学分析方程的统一,可以通过多体理论中坐标转换矩阵 B,实现有限元分析方程向多体系统动力学的转换。对于形如上式的有限元方程,其惯性坐标下的刚度、阻尼、质量矩阵,是由局部坐标系的响应矩阵乘以局部坐标向惯性坐标的转换矩阵得到的。即上述方程可以表示为:

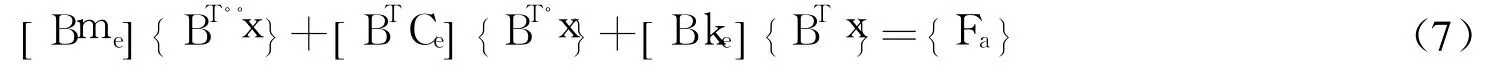
同时,上述方程的等号右边也可以表示为位移、速度、加速度的函数:

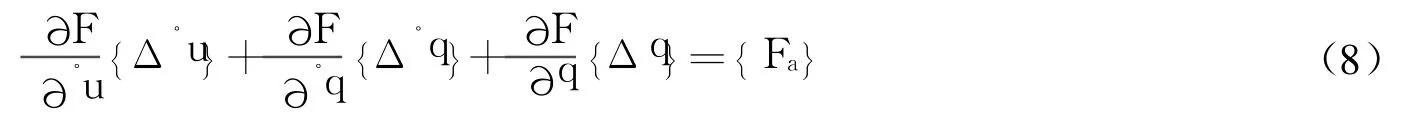
当单元的位移不大时,采用惯性坐标描述方程应是简单可行的方法,因为转换矩阵不需要更新。但当单元位移较大时,转换矩阵必须更新,从而使得局部坐标向惯性坐标系转换的相关矩阵也必须更新,如此系统的求解效率就明显降低。

在 Adams软件中,所有的刚体与柔体都使用一个随刚体和柔体运动的浮动局部坐标(Local Floating Reference Frame),当刚体或柔体运动时,对于系统求解的每一步,从局部坐标向惯性坐标系转换的相关矩阵也必须更新,但惯性坐标系下的矩阵不需要重新形成,从而提高了系统的求解效率。对于集成有限元模型的多体系统的求解是在多体模型的基础上,预先求得柔性体与多体系统的作用点的力、力矩、位移、速度、加速度等边界条件,柔性体以此边界条件求出变形与力、力矩,与多刚体模型的结果进行对比,如果误差较大,可进入下一步求解,此时以柔性体的变形或力、力矩为已知条件,求得系统对此作用点相应的力、力矩或位移,直到误差达到规定的范围。

3.2 曲轴受迫振动分析

3.2.1 曲轴扭转振动产生的机理 当柔性轴受到外界扭转力矩作用时,会产生弹性变形,这种变形的绝对值在一般情况下是不大的,但是当外界扭转力矩的频率与轴的共振频率相同时,轴的扭转变形幅度将大大超过正常值,这种现象就是轴的扭转共振[8]。

由于曲轴系本身不仅具有惯性,而且还有弹性,由此确定了其固有的自由振动特性。曲轴本身是由连杆作用在各个曲拐上的周期变化的扭矩 M驱动旋转的,它是由作用在活塞上的气体压力所产生的扭矩 Mg和由往复惯性力所产生的扭矩 Mj复合而成的。虽然这两个扭矩都是周期变化量,但都不是按简谐规律变化的,因此可以用数学方法分解成一系列简谐量之和。当在某一转速下,施加在曲轴上的周期变化的某一阶简谐力矩与曲轴本身的扭转振动频率相同时,曲轴就会产生所谓的共振现象。

3.2.2 曲轴强迫扭转载荷的施加 曲轴系存在阻尼,会使自由扭转振动逐渐衰减,直到振动停止。系统要维持持续振动,必须从外界输入能量,以弥补阻尼所消耗的能量。在干扰力矩的作用下的持续振动,称为强迫振动。干扰力矩对系统的作用取决于干扰力矩的大小和它随时间变化的规律。其中干扰力矩随时间变化的规律在许多情况下显得更为重要。作用在发动机曲轴系统上的干扰力矩,一般都是按周期性规律变化的,可以分解为傅立叶三角级数的形式,利用线性系统所满足的叠加原理,分别考虑其中各次谐波干扰力矩对传动系统所产生的作用,然后再叠加起来确定系统的振动规律。

干扰力矩的计算公式:

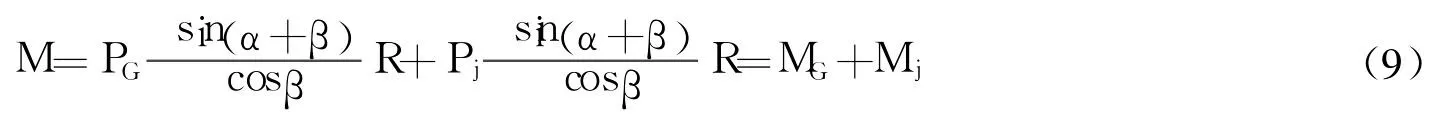
式中,MG为燃气爆发压力产生的力矩;Mj为往复惯性力产生的力矩;α为以上止点为基准的曲柄转角;β为连杆中心线与汽缸中心线之间的夹角;R为曲柄半径。

在传统的曲轴扭转强迫振动分析中,利用傅立叶级数把周期性变化的燃气爆发压力产生的力矩 MG展开为扭矩的平均值和一系列具有不同振幅、不同频率、不同初相位的简谐力矩之和,然后施加在曲轴上。发动机曲柄连杆机构的惯性力有离心惯性力和往复惯性力两种。由于离心惯性力通过曲轴的回转中心,对曲轴不产生扭转振动的激振力矩。而往复惯性力和燃气压力一样,它们作用在活塞及连杆上,并通过连杆传到连杆轴颈,对曲轴产生周期性变化的切向力矩,此力矩会激起曲轴系统的扭转振动。

3.2.3 曲轴强迫扭转载荷的分析 利用前面建立的完整曲轴系仿真分析模型,可以在 Adams/Vibration中实现对曲轴系的强迫扭转振动分析,既能提高工作效率又有较高的分析精度。作用在曲轴系的外力主要是燃气爆发压力,同时还需要考虑活塞与气缸的摩擦。燃气爆发压力通过示功图得到,按照发动机的工作顺序 1-3-4-2施加在活塞顶部(图 1)。

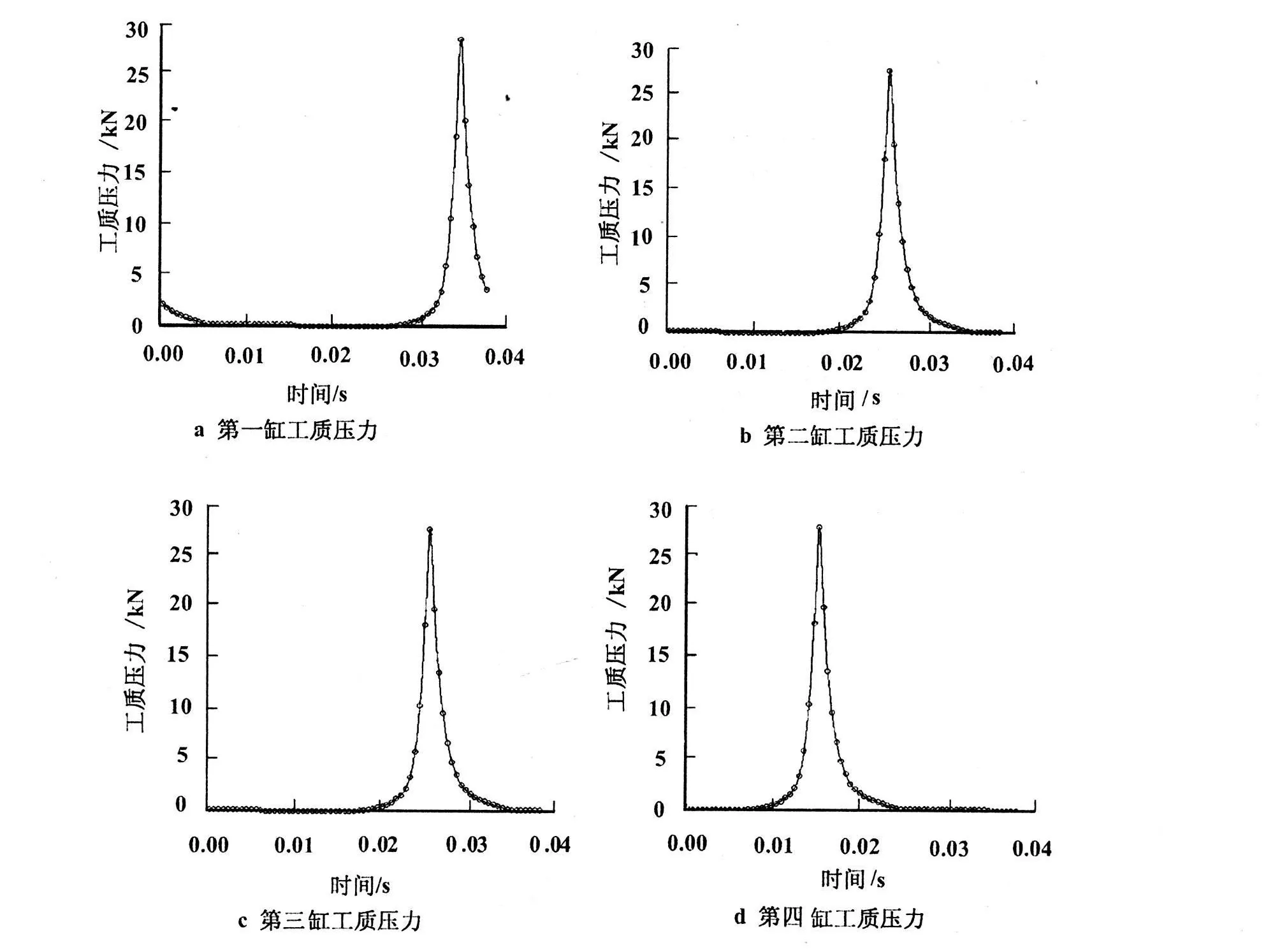
图 1 发动机燃气爆发压力

将图 1所示各缸爆发压力施加于各活塞顶部,活塞将力传给连杆,连杆最终将力施加给各连杆轴颈。从曲轴自由端向右,连杆轴颈依次编号 1,2,3,4,则各连杆轴颈处受力如图 2所示。

在 ANSYS中生成曲轴模态中性文件,导入 ADAMS/View中创建曲轴柔性体模型,将建立的曲轴轴系多刚体动力学模型中的刚性曲轴替换为柔性曲轴。施加爆发压力和控制曲轴转速后,即生成曲轴轴系柔性多体动力学模型。对曲轴轴系柔性多体动力学模型进行发动机稳定工况下的动力学仿真,得到曲轴在一个工作周期内的仿真数据(图 3,图 4)。

图 3是第二曲柄臂与第一连杆轴颈之间圆角处的合位移变形曲线,其变形主要是由于第一缸爆发压力所引起的。图4是此圆角处变形的合速度变化曲线。由图 3和图 4可知:(1)柔性曲轴在受迫振动的初始阶段会有较大的振幅波动,但这一时间持续很短,一般在曲轴旋转第 1周的时间之内,之后曲轴振幅趋于稳定;(2)柔性曲轴在受迫振动的初始阶段由于受到来自连杆的瞬时冲击力,速度变化很快,速度变化波动比较大。但持续时间也很短,一般是在曲轴旋转 1周的时间之内完成波动,之后速度变化趋于稳定。

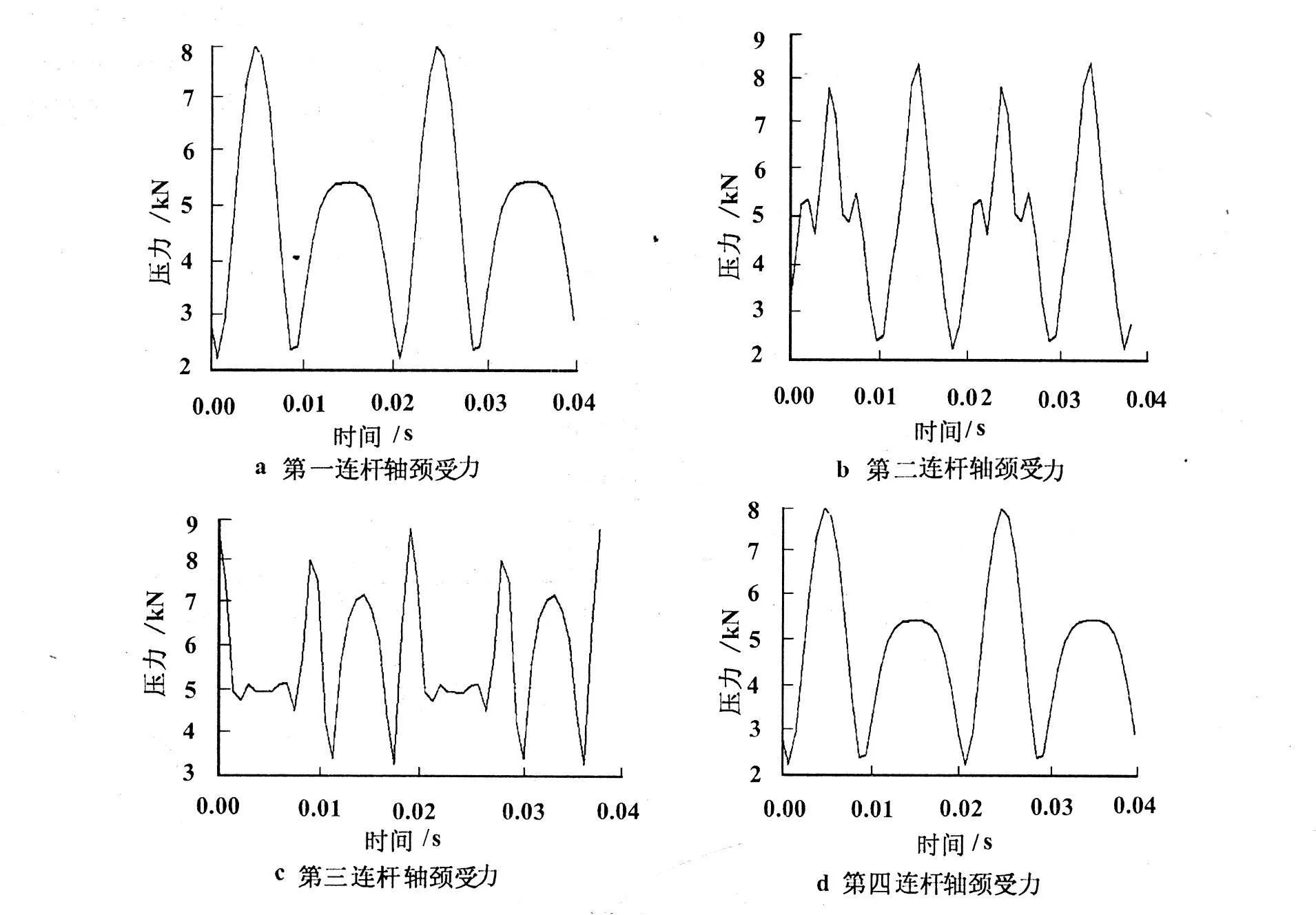
图 2 连杆轴颈受力

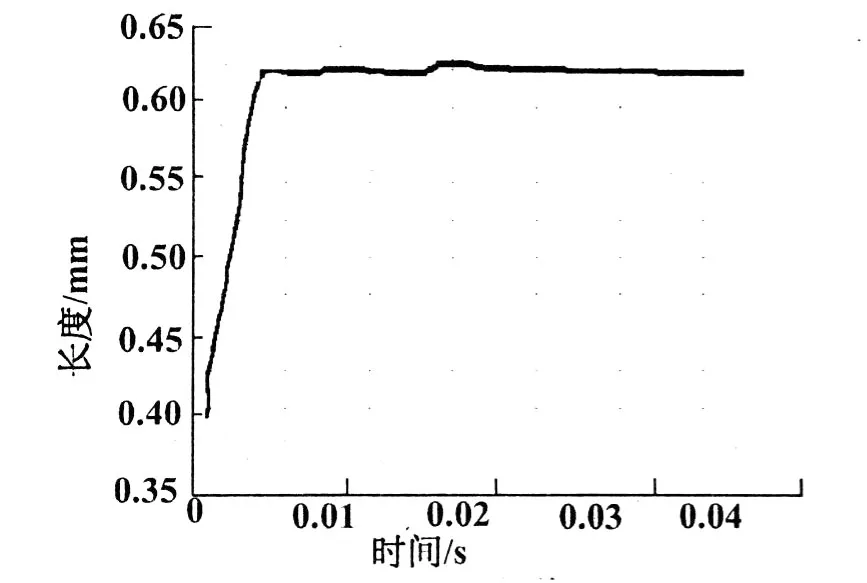
图 3 合位移

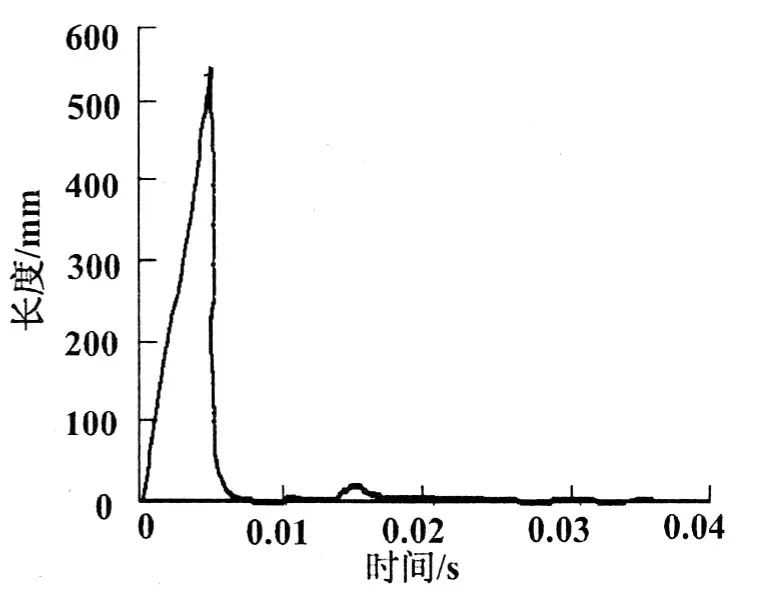
图 4 合速度

4 结 论

在建立了刚柔耦合曲轴系模型的基础上,按照给定的加载方式,对发动机曲轴系的扭转振动做了动态仿真分析。仿真结果表明,在给定加载条件下,曲轴在圆角处的合位移及合速度有一突变,即圆角处所受振动剧烈,易产生变形,与实际相符。利用本分析方法所得到的曲轴受迫震动仿真分析结果,可用于后续的曲轴振动噪声分析计算。

[1] CLARK,NIJEL.Operation ofa Small Bore Two-Stroke Linear Engine[J].ASME,1998:251-262.

[2] 尤小梅.发动机曲轴动力学仿真[D].沈阳:沈阳理工大学,2004.

[3] 李震,桂长林,孙军.内燃机曲轴轴系振动分析研究的现状、讨论与展望[J].内燃机学报,2002,2(5):469-474.

[4] 陈立平,张云清,任卫群,等.机械系统动力学分析及 ADAMS应用教程[M].北京:清华大学出版社,2005.

[5] 刘景阳,洪嘉振.柔性体的刚柔耦合动力学分析[J].固体力学学报,2002,23(2):159-166.

[6] 叶先磊,史亚捷.ANSYS工程分析软件应用实例[M].北京:清华大学出版社,2003.

[7] A R Mc Health,PM Namara.Crankshaft Stress Analysis Combination of Finite Elementand Classical Analysis Techniques Trans ASME JEng[J].Fro Gas Turbines and Power,1990,112(7):268-275.

[8] 祝效华,廖伟志,黄永志,等.CAD/CAE/CFD/VPT/SC软件协作技术[M].北京:中国水利水电出版社,2004.

[9] 雷宣扬.内燃机曲轴动态振动特性模拟及其裂纹故障分析[D].大连:大连理工大学,2003.

(责任编辑:石瑞珍)