Zn2 SiO4电子结构及光学性质的第一性原理计算

张志伟,潘 勇,廉 琪,沈喜海,邵丽君,张卫国,3*

(1河北科技师范学院理化学院,河北秦皇岛,066600;2昆明贵金属研究所;3燕山大学材料科学与工程学院)

Zn2SiO4作为发光材料,与硫化物发光材料(如 ZnS,SrS等)相比,环境适应性强,化学稳定性好,抗湿性强,而且易于制备,价格低廉,因此在发光材料研究中倍受关注。Zn2SiO4是一类含有有限硅氧基团的硅酸盐,一个单独的硅氧四面体与 Zn离子结合形成互不相连接的孤立四面体。荧光显示 Zn2SiO4对244 nm的紫外光有很微弱的吸收,并在 252 nm处发出极微弱的荧光[1～7]。

国外,S.Zh.Karazhanov等[8]采用局域密度泛函理论对四方和立方结构的 Zn2SiO4进行了电子结构和光学性质等的计算,计算表明禁带宽度在2.22～4.18 eV之间。还有一些研究者在 Zn2SiO4里掺杂其它离子,采用第一性原理进行了计算。例如,K.C.Mishra等[9]采用第一性原理的方法研究了掺杂 Mn离子的电子结构,H.D.Park等[10]采用第一性原理的方法研究了掺杂 Co离子的电子结构和光致发光效应。在国内,ZHANGHua[11]采用局域密度泛函理论和第一性原理的方法,计算四方结构和三斜结构硅酸锌的平衡晶格常数、电子态密度和能带结构,能带计算表明,三斜结构硅酸锌均为直接带隙半导体,禁带宽度 2.89 eV。

然而,对三斜结构的 Zn2SiO4光学性质方面的研究还未见报道。鉴于此,本研究采用目前计算机模拟实验中较先进的基于密度泛函理论(DFT)的赝势平面波方法对三斜结构的 Zn2SiO4的能带结构、态密度、介电函数、折射率及吸收系数、光电导率等光学性质进行了全面的计算,并对其机理进行了较为详细的分析。因此,对 Zn2SiO4的电子结构和光学性质研究显得尤为重要。

1 理论模型和计算方法

1.1 理论模型

选用的计算模型是具有三斜结构的Zn2SiO4,它属于 R-3的空间群,晶格常数为 a=b=1.395 nm,c=0.931 nm[12]。该计算体系中总共 42个原子,分别为:24个 O原子,6个 Si原子和 12个 Zn原子,晶胞结构如图 1所示。

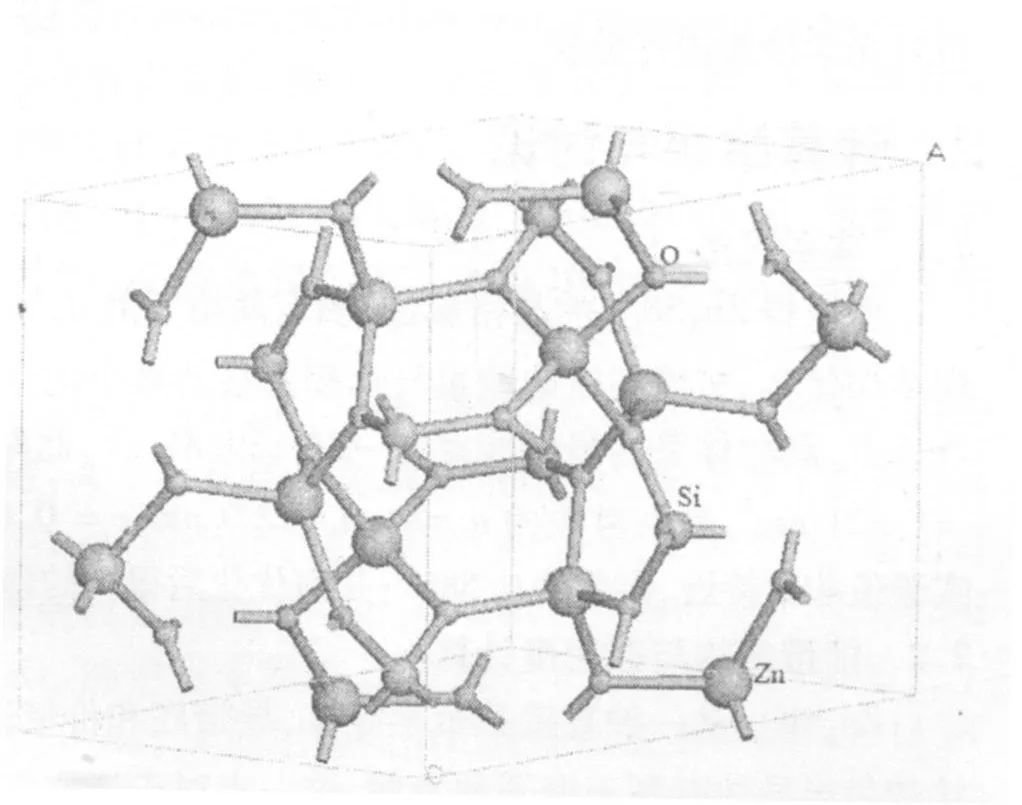
图 1 Zn2SiO4晶体结构示意图

1.2 计算方法

本研究所有的计算都是由 Material studio 4.0中的 CASTEP软件(Cambridge sequential total energy package)[13]完成的。CASTEP软件是一个基于密度泛函方法的从头算量子力学程序。利用总能量平面波赝势方法,将离子势用赝势替代,电子波函数通过平面波基组展开,电子—电子相互作用的交换和相关势由局域密度近似(LDA)或广义梯度近似(GGA:generalized gradientapproximation)进行校正,它是目前较为准确的电子结构计算的理论方法。

计算采用的晶格常数都为实验值,首先采用 BFGS算法(由 Broyden和 Fletcher等提出的一种能对固定外应力的晶胞进行优化的算法)[14～17]对晶体模型进行结构优化,将原胞中的价电子波函数用平面波基矢进行展开,并设置平面波截断能量 Ecut=310 eV,迭代过程中的收敛精度为 1×10-6eV。选取广义梯度近似(GGA)来处理交换关联能部分,交换关联势采用超软(ultrasoft)赝势[18],Brillouin区积分采用 Monkhors-Pack[19]形式的高对称特殊 k点方法,k网格点设置为 7×7×4,能量计算都在倒易空间中进行。

1.3 光学性质的理论描述

在线性响应范围内,固体宏观上以由光的复介电函数 ε(ω)=ε1(ω)+iε2(ω)或复折射率 N(ω)=n(ω)+ik(ω)来描述 ,其中

由于电子结构计算中无论是带间还是带内跃迁都远大于声子频率,且使用的方法是单电子近似法,故可以忽略声子在间接跃迁过程的参与,仅考虑电子激发。从量子力学的观点看,带间跃迁光吸收过程是电子在辐射电磁场微扰作用下从低能态跃迁到高能态的过程。从直接跃迁几率的定义可推导出晶体介电常数虚部为[20]:

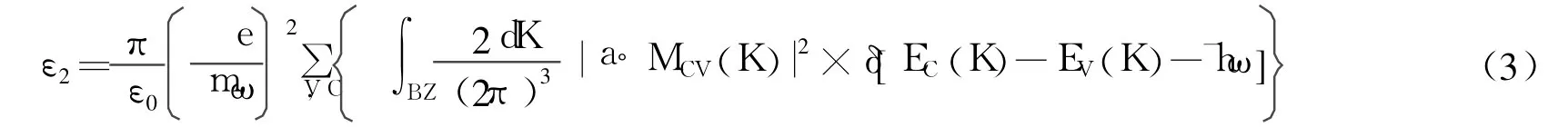
其中,C和 V分别表示导带和价带,BZ为第一 Brillouin区,K为倒格矢,|a·MCV(K)|2为动量跃迁矩阵元,EC(K)和 EV(K)分别为导带和价带上的本征能级,ω为角频率。(3)式表明固体的宏观光学常数与其微观能带结构、跃迁矩阵元和状态密度相联系,因此,固体的能带结构,利用 Kramers-Kronig色散关系就可对固体的各种宏观光学常数如折射率 n(ω),吸收系数 α(ω)和反射率 R(ω)等进行计算,并可对光学性质进行分析。

2 计算结果与讨论

2.1 体系优化

为获得 Zn2SiO4的晶格属性,确定晶格常数 a,b和c,利用实验晶格参数对Zn2SiO4超原胞进行了几何结构优化,按照超原胞能量与体积关系的最小化原理得超原胞的晶格结构参数(表 1)。优化计算后,Zn2SiO4晶胞体系的最低能量为 -31 839.86 eV,此时其晶胞处于最稳态,与最稳态对应的晶胞体积为 V=1.821 nm3,晶格常数为 a=b=0.432 9 nm,c=0.625 5 nm。几何优化后得到的理论晶胞体积参数与实验值非常接近,误差为 0.58%;几何优化后得到的理论晶胞参数与实验值非常接近,误差小于 0.27%。

2.2 能带结构与态密度计算

Zn2SiO4是一种直接禁带半导体,导带底和价带顶位于 Brillouin区的 Γ点处(0.420 78)(图 2)。直接禁带半导体有利于电子的发射,这一点对于光电仪器或光学仪器十分重要。因此,基于以上所述的特点,适合做短波的探测器和发射器。计算的带隙值(Eg)为 3.12 eV,这一数值其他人模拟计算相接近,例如 ZHANG Hua[11]模拟计算的数值是 2.89 eV,然而,与实验结果(5.5 eV)比较,这一带隙值偏小,这主要是由于广义梯度近似与局域密度近似都存在 Eg计算值偏低的普遍性问题。这主要是计算中过高地估计了 Zn3d的能量,造成 Zn3d与 O2p相互作用的增大,结果使价带带宽增大,带隙偏低,但这并不影响对 Zn2SiO4电子结构的理论分析。计算得到 Zn2SiO4总态密度(图3)。对于总态密度,单位是 electrons/(celleV),对于各亚层电子的能态密度,单位是 electrons/(atom eV)。从图中可以看出价带分为两部分,上价带在 -7.5～0 ev之间,Zn2SiO4的态密度主要由 Zn的 3d态电子和 O的 2p态电子构成,Si的 3s和 3p态电子贡献也很明显,Zn的 3p和 4s态电子也有作用,但作用很小。O的 2p态电子参与了与 Si的 3s及 3p态电子的杂化,同时与 Zn的 3d态电子发生了杂化。下价带在 -16.5～19.0 ev之间,Zn2SiO4的态密度主要由 O的 2s态电子构成,Si的 3s和 3p态电子也有所贡献。O的 2s态电子参与了与 Si的 3s,3p和 Zn的 3p,4s的成键过程。导带在 6.5～7.5 ev之间,起主要贡献的是 Zn的 3p和 4s态电子,Si的 3s和 3p态电子贡献比较小。

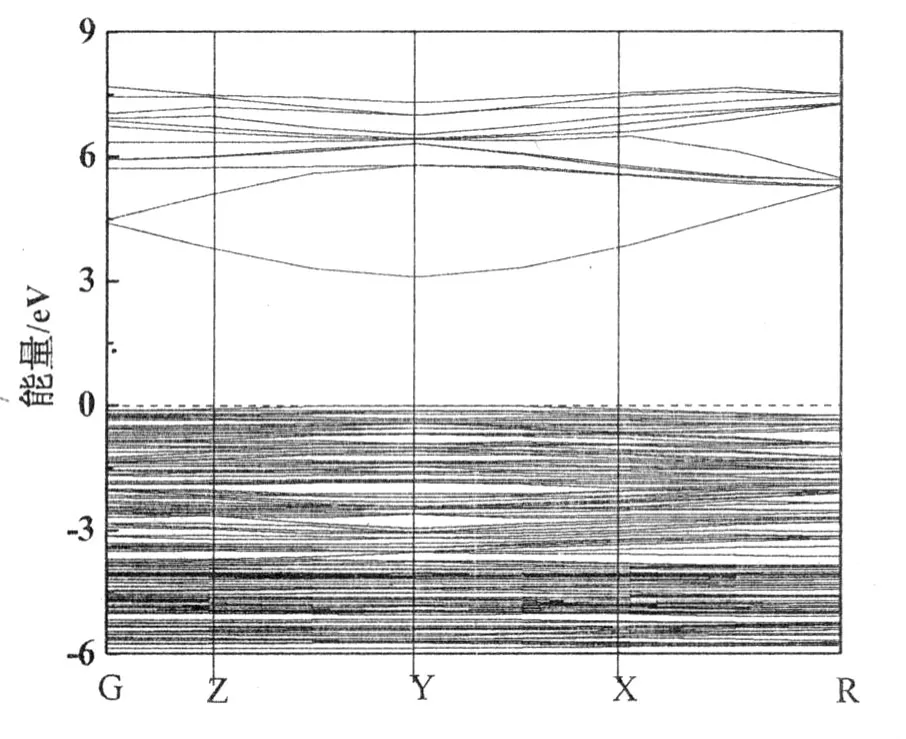
图 2 Zn2 SiO4能带

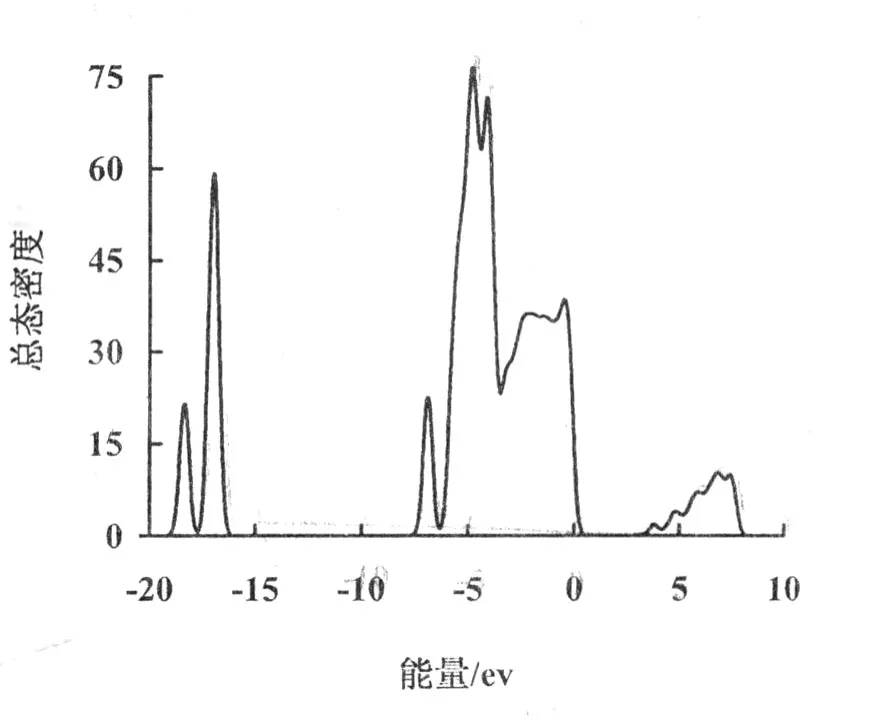
图 3 Zn2 SiO4总态密度

2.3 光学性质

2.3.1 复介电常数 介电函数作为沟通带间跃迁微观物理过程与固体电子结构的桥梁,反映了固体能带结构及其他各种光谱信息。Zn2SiO4作为半导体材料,其光谱是由能级间电子跃迁所产生的,各个介电峰可以通过 Zn2SiO4的能带结构和态密度解释。采用 DFT赝势平面波方法计算得到非极化的Zn2SiO4光学介电函数的实部 ε1和虚部 ε2的变化曲线(图 4)。计算得到的静态介电常数 ε1(0)=1.793。在能量为 7.18 eV处 ε2达到峰值,这主要是由最高的价带到最低的导带间的电子跃迁产生的。

2.3.2 吸收系数 吸收系数表示光波在介质中单位传播距离光强度衰减的百分比。利用介电函数和吸收系数的关系 α=(ω/nc)·ε2可以得到 Zn2SiO4的吸收系数(图 5)。在能量低于 2.16 eV以及能量大于 15.54 eV的范围,Zn2SiO4对光的吸收为 0,表明在波长大于 574 nm和波长小于79.8 nm的范围是透明的。吸收系数在能量为 9.04 eV处达到最大峰值 8.56×104cm-1,能量大于 9.04 eV后,吸收系数随着光子能量的增加逐渐减小,当达到光子能量 11.53 eV时达到次峰 7.90×104cm-1,随后吸收系数随着光子能量的增加逐渐减小到 0。

2.3.3 复折射率 由复折射率和介电函数的关系 ε1=n2-k2,ε2=2nk,得到 Zn2SiO4复折射率。折射率 n0=3.35(图6)。n的主要峰值出现在能量2.45～4.15 eV范围内,最大峰值处对应的光子能量的值为 3.37 eV,此时折射率 n=1.47,光子能量大于 3.37 eV后折射率逐渐减小,在能量为 12.90 eV时折射率 n值达到最小,此时,n=0.59。吸收系数和消光系数之间的关系为 α=2kω/c=4kπ/λ0。 λ0为光电磁波在真空中的波长。与吸收系数相对应,Zn2SiO4的消光系数在能量低于 2.16 eV以及能量大于15.54 eV的范围内为 0,当能量为 7.79 ev时,k值为 0.61。k的主要峰值出现在能量为 7.25～9.15 eV范围内,能量大于 7.79 eV后消光系数随光子能量的增加而减小,在光子能量达到 15.54 eV时消光系数 k减小到 0。当光子能量大于 15.54 eV时,入射光频率不小于固有振荡频率,此时,表征固体吸收的光学量都趋近于 0,折射率随频率的变化为正常色散,Zn2SiO4再次转变为透明的,同时,消光系数在带边表现出强烈的吸收特征。

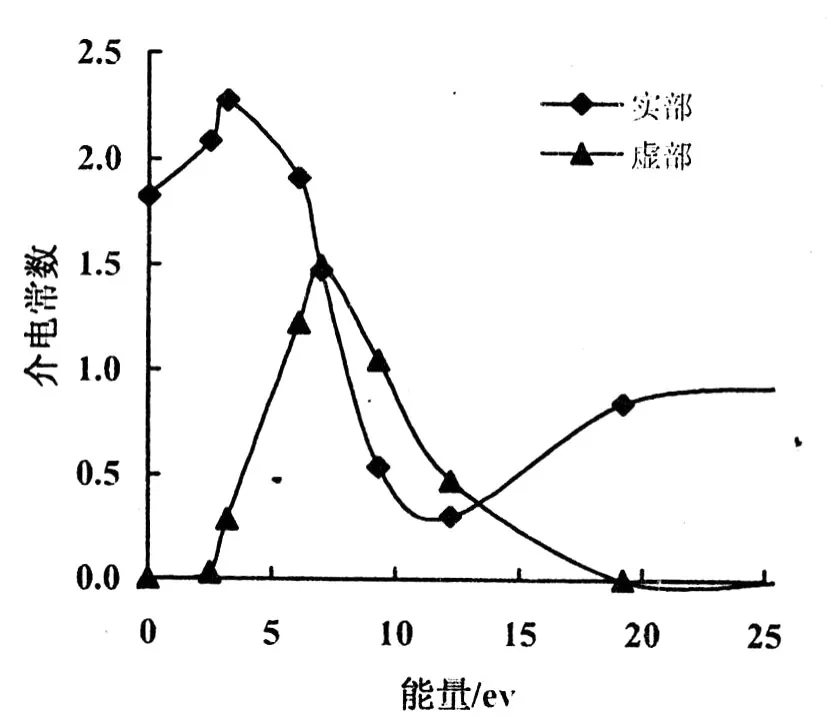
图 4 Zn2SiO4介电函数的实部 ε1和虚部 ε2

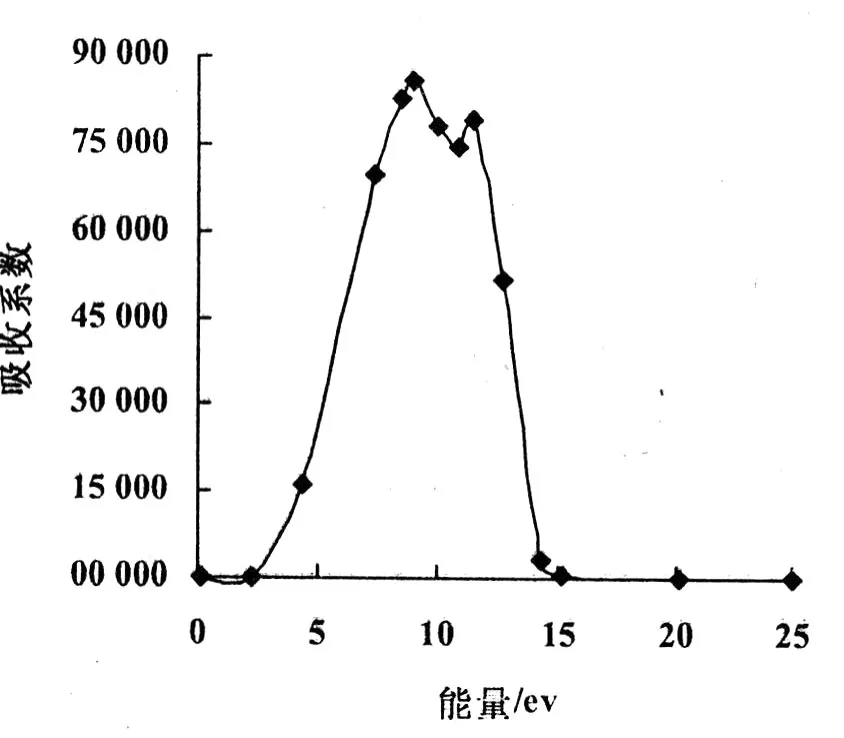
图 5 Zn2SiO4的吸收系数

2.3.4 光电导率 半导体的光电导是指光照引起半导体电导率改变的现象,这种改变可以是电导率的增加,也可以是电导率的下降。光电导效应是半导体各种光电子应用(如辐射的探测和测量、太阳能光电能量转化等)的物理基础。Zn2SiO4的光电导率的实部在能量低于 2.16 eV以及能量大于 15.54 eV的范围内为 0(图 7),主要峰值出现在 7.25～9.15 eV的能量范围内,与前面的吸收系数和消光系数的峰值出现的位置完全对应,验证了光电导率的实部与吸收系数的关系。

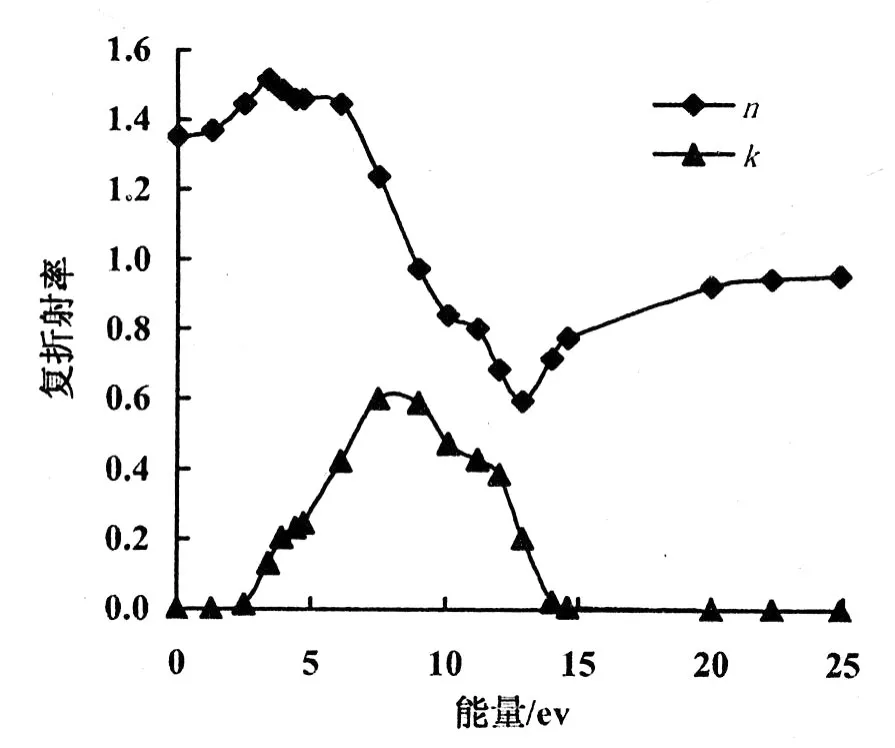
图 6 Zn2SiO4的复折射率

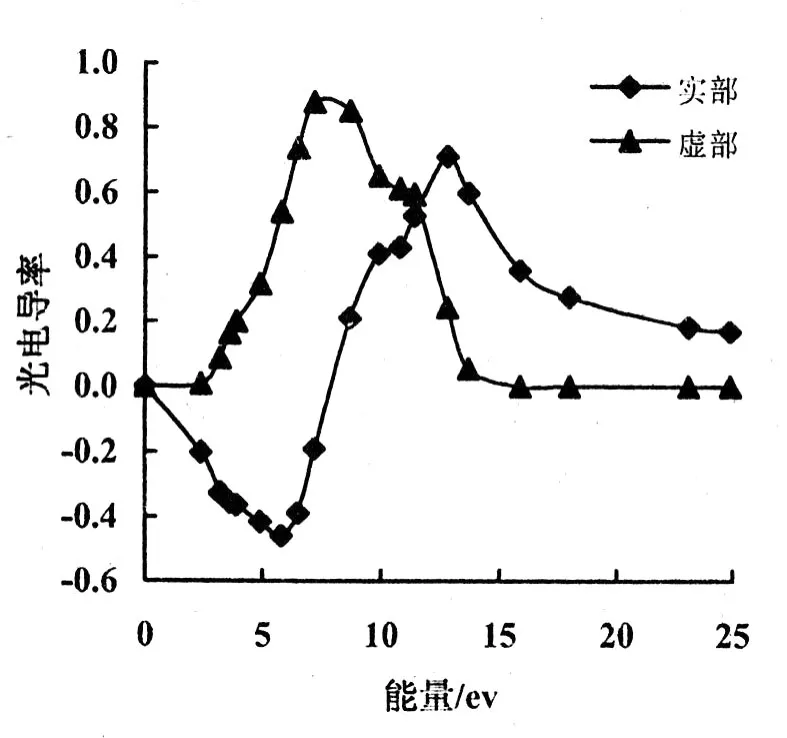
图 7 Zn2 SiO4的光电导率

3 结 论

本研究使用基于第一性原理的密度泛函理论(DFT)赝势平面波方法,对三斜结构的 Zn2SiO4的能

带结构、态密度和光学性质进行了理论计算。能带计算结果表明,Zn2SiO4为直接带隙半导体是其具有

较好的光学性质的主要因素;对光学性质计算表明,在不同能量范围,介电函数、吸收谱、复折射率、光导

电率等性质表现出互相印证的关系。

[1] CHANG JUNKIM,MYOUNG SEOK KWON.Effects of Water Content in an Ethanol-based Solvent on Sol-gel Synthesis of Zn2SiO4:Mn Phosphors[J].Electronic Materials Letters,2009,5(3):113-117.

[2] JAE-SUL AN,JUN HONGNOH,IN-SUN CHO.Tailoring the Morphology and Structure of Nanosized Zn2SiO4:Mn2+Phosphors Using the Hydrothermal Method and Their Luminescence Properties[J].The Journalof Physical Chemistry C,2010,114(23):10 330-10 335.

[3] XU G Q,XU H T,ZHENG Z X.Preparation and characterization of Zn2SiO4:Mn phosphors with hydrothermal methods[J].The Journal of Physical Chem istry C,2010,114(23):10 330-10 335.

[4] DIAO CC,YANG C F.Synthesis ofhigh efficiency Zn2SiO4:Mn2+green phosphors using nano-particles[J].Ceramics International,2010:36(5):1 653-1 657.

[5] YU X,WANG Y.Synthesis and photolum inescence improvement of monodispersed Zn2SiO4:Mn2+nanophosphors[J].Journal of Alloys and Com pounds,2010:497(1):290-294.

[6] YUE Z,DONGM,MENG S.Phase Characterization and Dielectric Properties of Zn2SiO4Ceramics Derived from a Sol-Gel Process[J].Ferroelectrics,2009(387):184-188.

[7] ZHANG JM,ZHAO D L,SHEN ZM.Synthesis and Lum inescent Properties of Mn2+-Doped Zinc Silicate Phosphors by Sol-Gel Method[J].Key Engineering Materials,2010,434:214-216.

[8] SZ H KARAZHANOV,PRAVINDRAN,H FJELLVAG.Electronic structure and optical properties of ZnSiO3and Zn2SiO4[J].Journal of App lied Physics,2009,106:123 701.

[9] K C MISHRA,K H JOHNSON,B G DEBOER,et al.First princip les investigation of electronic structure and associated p roperties of zinc orthosilicate phosphors[J].Journal of Lum inescence,1991,47:197-206.

[10] H D PARK,K-SSOHN,BCHO.Effect of Co-doping on the Photolum inescent Behavior and Electronic Structure of Zinc Silicate Phosphors[J].Materials Research Society,1999,560:3-8.

[11] ZHANG HUA,FENG XIA,KANG JUN-YONG.Electronic Structures of Zn2SiO4[J].Chinese Journal of Lum inescence,2006,27(5):750-754.

[12] K H KLASKA.New investigations ofwillemite[J].Acta Cryst,1978,34:3 324.

[13] SEGALLM D,Philip Lindan JD,ProbertM J,etal.First-p rinciples simulation:Ideas,illustrations and the CASTEP code[J].J Phys Rev-CondensMatter,2002,14(11):2 717-2 744.

[14] BROYDEN CG.The convergence of a class of double-rank minimization algorithms,the new algorithm[J].J Inst Math Appl,1970,6:222-231.

[15] FLETCHER R.A new approach to variab lemetric algorithms[J].Comput J,1970,13(3):317-322.

[16] GOLDFARBD.A family of variab le-metric methods derived by variationalmeans[J].Math Comput,1970,24(109):23-26.

[17] SHANNO D F.Conditioning of quasi-Newton methods for functionm inimization[J].Math Comput,1970,24:647-656.

[18] VANDERBILT D.Soft self-consistent pseudopotentials in generalized eigenvalue formalism[J].Phys Rev B,1990,41:7 892-7 895.

[19] 沈学础.半导体光谱和光学性质:第二版[M].北京:科学出版社,2002.

[20] 方容川.固体光谱学[M].合肥:中国科学技术出版社,2001.

(责任编辑:石瑞珍)