矩形钢管混凝土中核心混凝土的本构关系

郭小平

(湖南省交通科学研究院,湖南长沙 410015)

0 引言

随着我国桥梁建造技术的飞速发展,各种新型桥梁结构不断出现,钢管混凝土桁架在大跨径拱桥中的应用已经取得了巨大的成功。钢管混凝土结构利用钢管与混凝土在受力过程中的相互作用,可充分发挥两种材料的性能,具有承载力高、抗震性能好及施工简便的优点。就截面形式而言,虽然矩形钢管(设其截面边长h＞b)对核心混凝土的约束效应不如圆形、方形钢管显著,但由于矩形钢管混凝土具有抗弯刚度大、梁柱节点连接简单及便于空间布置等优点,在桥梁工程上也具有广泛的应用前景。

近年来,对图1—a所示的普通矩形钢管混凝土在不同受力状态下的力学性能已经进行了较多的试验研究。轴压试验结果表明截面长宽比h/b的增大对构件性能有不利影响[1～3],因此一些研究者为了增强矩形钢管对混凝土的约束作用,提出了设置加劲肋或约束拉杆等改进措施,并对这种改进的矩形钢管混凝土进行了试验研究[4],发现设置拉杆对构件承载力影响不大,但能较大程度地增强构件的延性,这对h/b＞2的构件来说意义尤为显著。

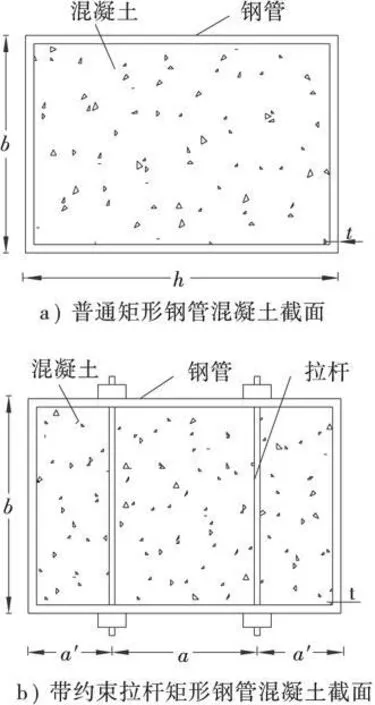
图1 矩形钢管混凝土截面

为了进一步明确构件的工作机理,一些研究者借助自编程序或大型有限元软件如ABAQUS等对普通矩形钢管混凝土构件进行了全过程分析。如李学平提出了等效约束效应系数的概念,建立了考虑钢管约束作用的核心混凝土单轴应力应变关系,采用纤维模型法对轴压构件分析的结果与试验结果符合较好[5]。Liang等建立了一个不考虑强度提高仅考虑延性增加的核心混凝土本构模型,也利用纤维模型法对试验结果进行了验算[6]。与此同时,蔡健等借鉴Mander模型的研究思路,给出了带约束拉杆矩形钢管约束下的核心混凝土本构关系,其合理性得到了试验结果的验证[7]。陈曦将素混凝土的单轴应力—应变关系应用到对带约束拉杆矩形钢管混凝土轴压试件的ABAQUS分析中,模拟结果与试验结果相差较大[8]。这也说明在建立适用于ABAQUS分析的核心混凝土本构关系时,需同时考虑钢管的约束作用所引起的混凝土强度及延性的增加。

在应用ABAQUS对矩形钢管混凝土构件进行分析时,关键是建立合理的核心混凝土本构关系,韩林海[1]、Schneider[2]及Ellobody[9]在这一方面做了较多工作,基于不同方法提出了各自的本构模型。但不足之处是上述几种本构关系均适用于普通矩形钢管混凝土,而不易推广到带约束拉杆或其他改进形式的矩形钢管混凝土中。为解决这一问题,本文提出了基于体积的核心混凝土强、弱约束区划分方法,修正了Mander约束混凝土模型中有效侧向约束系数、核心混凝土强度和下降段的表达式,建立了同时适用于对普通矩形钢管混凝土和带约束拉杆矩形钢管混凝土进行ABAQUS分析的核心混凝土本构关系,通过对这两种截面形式的短柱轴压试验的模拟验证了该本构关系的合理性,为构件性能的深入研究提供了参考。

1 核心混凝土本构关系

1.1 有效侧向约束系数

矩形钢管约束下的核心混凝土处于较为复杂的三向受力状态,从横向来看,约束作用主要集中在横截面角部,并且两个方向(沿长边或短边)不等;从构件纵向来看,约束作用在靠近端部处较大而发展到柱中处时较小。这与构件受压时主要产生半波式的外鼓变形是一致的。设置约束拉杆(一般沿长边设置)能有效地约束钢管的横向变形,使设置拉杆的面的变形无论沿横向还是纵向均呈现多段半波的趋势。

Mander建立箍筋约束混凝土本构关系的思路是:将核心混凝土沿横向和纵向按截面积分别划分强、弱约束区,计算出对应的有效侧向约束系数,取二者之积作为构件的有效侧向约束系数ke[10]。该方法的优点是力学概念较为清晰,适用性强,蔡健在研究带约束拉杆钢管混凝土时也采用了这一研究方法[7、11,12]。根据上述对两种构件的约束机理的分析,本文提出基于体积的核心混凝土的强、弱约束区划分,同时ke采用体积比进行计算。

1.1.1 普通矩形钢管混凝土的有效侧向约束系数

设沿矩形截面长边方向为x轴,沿短边方向为y轴,沿构件纵向为z轴。为了计算简便,将横截面上的约束区界线简化成折线,图2—a所示为矩形钢管约束下核心混凝土的强约束区示意图,即混凝土端面全截面均为强约束区,柱中截面的强约束区面积最小。设柱高为L,核心混凝土的体积为:

设柱中截面上强、弱约束区界线底角均为θ(见图2—

c),即弱约束区相当于四个棱锥体,可得强约束区体积为:

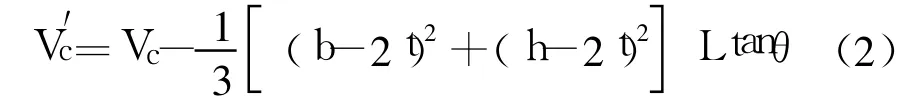
则有效侧向约束系数为:

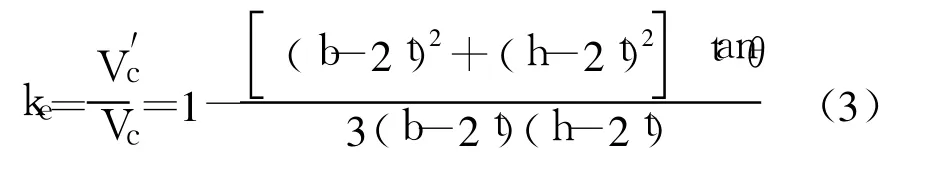
图2 普通矩形钢管混凝土中核心混凝土强、弱约束划分

1.1.2 带约束拉杆矩形钢管混凝土的有效侧向约束系数

一般而言,拉杆沿截面长边即在xz面内布置。设拉杆沿x轴设置m列,间距为a,拉杆与短边的间距为a′,则h=(m-1)a+2a′;沿z轴设置n排,间距为c,拉杆与构件端部的间距为c′,则L=(n-1)c+2c′。

设置约束拉杆对xz面内的约束区有较大影响,即yz面内的弱约束区不受其影响,仍为棱锥体。对xz面内的约束区可沿纵向、横向分段计算,即可将xz面简化成(m+1)×(n+1)个小矩形,其中边长为a′×c′的为4个;a×c′的为2(m-1)个,a′×c的为2(n-1)个,a×c的为(m-1)×(n-1)个,假定核心混凝土两端面及拉杆所在截面均为强约束区,相邻拉杆或拉杆与端面的中间截面处强约束区最小,如图3所示。每一个小矩形按前述普通矩形钢管混凝土强、弱约束区划分方法来考虑,即其弱约束区均为小棱锥体,则在垂直于y轴方向的面内,弱约束区共由2(m+1)×(n+1)个小棱锥体组成。

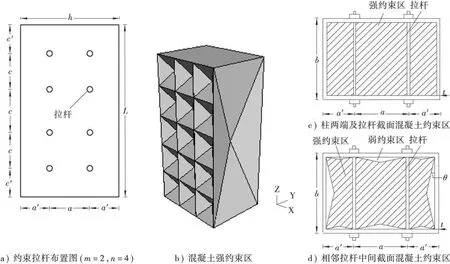
图3 带约束拉杆矩形钢管混凝土中核心混凝土强、弱约束区划分

因拉杆直径对构件性能影响不明显,可忽略拉杆体积的影响,则核心混凝土的体积为:

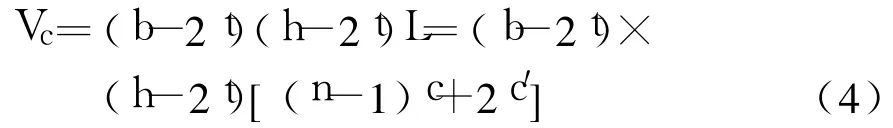
强约束区的体积为:

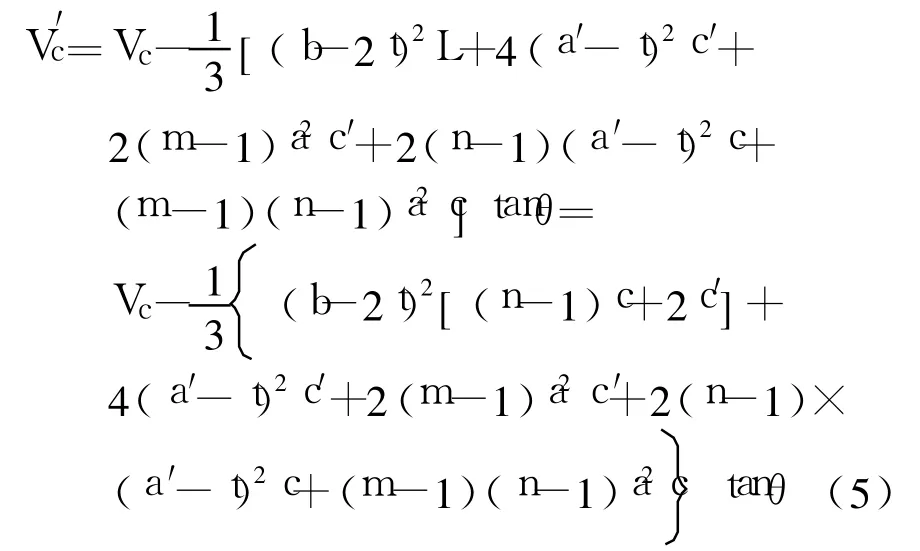
则有效侧向约束系数为:

1.2 有效侧向约束力

仍按Mander模型中的方法计算有效侧向约束力[10],两种构件中钢管长边及短边对核心混凝土平均侧向约束力不等,设其分别为f′1和f′2,而对应的钢板环向拉应力分别为为f″1和f″2,可由力学平衡条件得出f′1、f′2的表达式。

其中,矩形钢管混凝土中有:

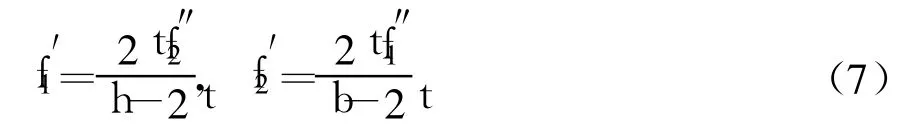
在带约束拉杆的矩形混凝土中,设拉杆强度为f′y,拉杆面积为A′s。若短边不设置拉杆时有:

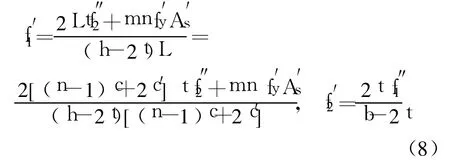
仍按照文献[7]中建议的方法计算钢管屈服时对应的f″1和f″2,不考虑钢管的局部屈曲,有f″1=f″2=0.19 fy,其中fy为钢管屈服强度。

则可以得到普通矩形钢管混凝土中长边和短边对核心混凝土有效侧向约束力为:

带约束拉杆矩形钢管混凝土中的长边和短边对核心混凝土的有效侧向约束力为:

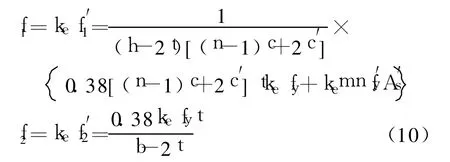
1.3 核心混凝土极限强度及峰值应变

文献[7]中采用过-王五参数强度准则计算核心混凝土的极限强度,较为精确但计算不太方便。鉴于不论在普通矩形钢管混凝土还是带约束拉杆矩形钢管混凝土中,核心混凝土所受的整体约束作用f应介于f1和f2之间,设Ac为核心混凝土面积,则当Ac=(h-2t)2或(b-2t)2时,截面均为正方形,对应的f分别与长边约束力f1、短边约束力f2相等,当(b-2t)2＜Ac＜(h-2t)2时,假定f按线性变化。即f满足以下关系:

对普通矩形钢管混凝土中核心混凝土的强度fcc,仍利用Mander模型的建议公式计算。即:

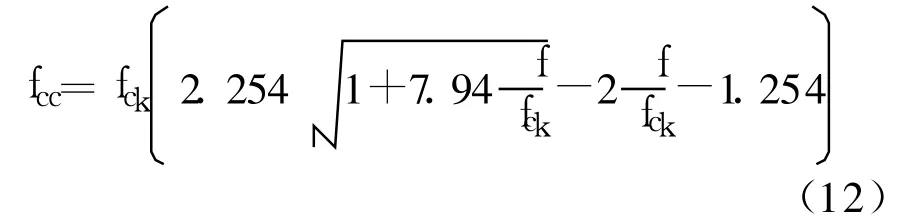
而对带约束拉杆的矩形钢管混凝土,经过试算,按William提出的强度公式[13]计算时结果较好。其表达式为:

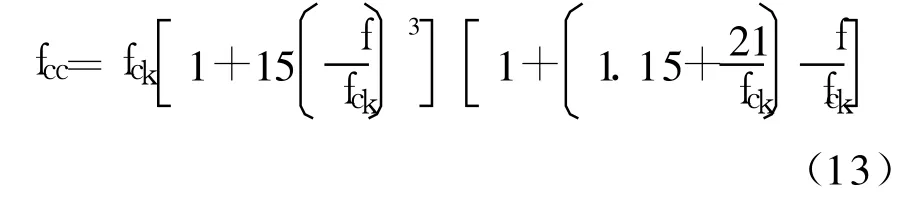
本文建议的峰值应变εcc计算公式为:

其中η为应变修正系数。对普通矩形钢管混凝土进行计算时,η的取值可与Mander模型一致,取η=5。设置拉杆后,由试验可知构件的峰值应变有较大程度的增加,此时可取η=6。

1.4 下降段

为便于计算分析,本文采用Schneider模型建议的双折线形式的下降段表达式[2],并定义下降段参数k来描述下降段的陡峭程度,普通矩形钢管混凝土的轴压曲线下降段的陡峭程度受其含钢率及材料性能影响较大,而设置拉杆后会使得构件的下降段更加平缓。在常用含钢率范围内,对h/b＜2的带约束拉杆矩形钢管混凝土,近似取k=0.4;而对h/b≤2的普通矩形钢管混凝土及h/b＞2的带约束拉杆矩形钢管混凝土,可取k=0.3。

综上所述,本文建立的核心混凝土的本构关系为:

式中:σ、ε为核心混凝土纵向应力和应变;fck为素混凝土抗压强度;fcc为核心混凝土抗压强度,对普通矩形钢管混凝土按式(12)计算,对带约束拉杆矩形钢管混凝土按式(13)计算;εcc为核心混凝土峰值应变,按式(14)计算;r为参数,按r=Ec/(Ec-Esec)进行计算;Ec为素混凝土弹性模量;Esec为核心混凝土割线模量,按Esec=fcc/εcc进行计算;k为下降段参数。

2 有限元分析及验证

2.1 有限元模型建立

本文搜集了10个普通矩形钢管混凝土(试件1～10)及16个带约束拉杆矩形钢管混凝土(试件11～26)短柱轴压试验的结果,试件的基本参数及承载力试验值列于表1,其中d为拉杆直径。为便于分析比较,混凝土强度统一换算成轴心抗压强度fck。应用ABAQUS软件对上述试件进行建模分析,混凝土采用塑性损伤模型,该模型适用于低围压下混凝土性能的模拟,受压时即采用式(15)的应力—应变关系,受拉时的应力—应变关系采用文献[2]中的受拉模型。钢材采用ABAQUS中的等向弹塑性模型,其弹性段及弹塑性段采用文献[1]的表达式,不考虑钢材的强化及二次塑流。两种材料的本构关系见图4。盖板刚度较大,因而采用刚性体模拟。考虑到计算的精度和经济性,钢板、混凝土和盖板均采用8节点三维减缩积分单元(C3D8R)。柱端面与盖板之间采用绑定约束,钢管和混凝土界面模型由切向滑移和法向接触两部分组成,沿接触面切向采用库仑摩擦及小滑移,剪切滑移系数取为0.25[14];沿接触面法向取为硬接触,允许材料分离但不允许互相穿透,能较好地模拟真实的界面性能。对约束拉杆建模时不考虑其与混凝土之间的接触关系,直接嵌固到整个模型中。在柱顶面盖板上采用位移加载的方式进行加载。

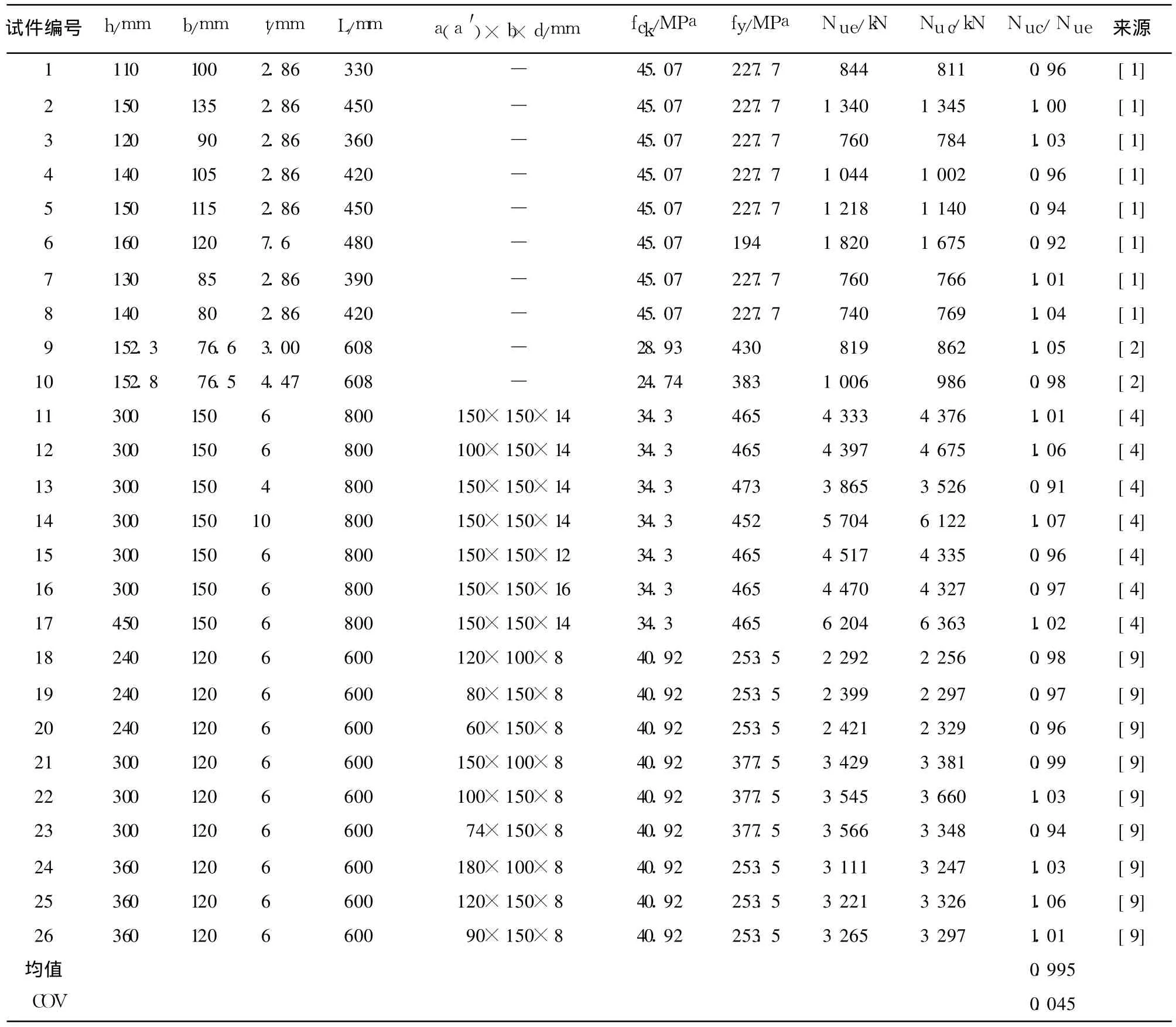
表1 试件参数及承载力表

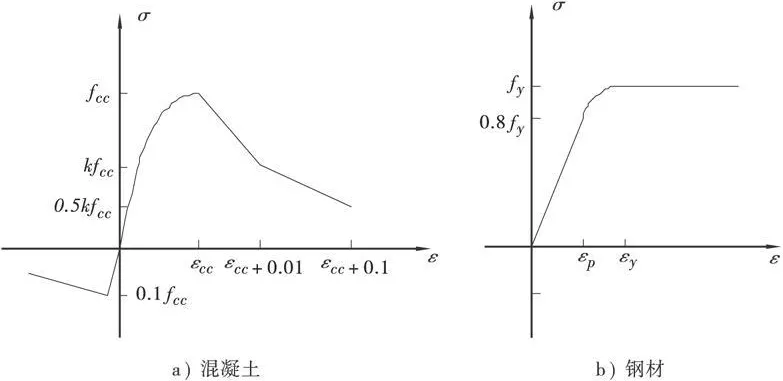
图4 材料本构模型

2.2 有限元模拟结果讨论

界线底角θ反映了钢管对核心混凝土约束作用的大小,按本文中的划分方法,θ不应大于45°即0.785 rad。由于在式(9)、式(12)及式(10)、式(13)中均考虑了材料强度对核心混凝土的影响,可认为θ仅与截面尺寸有关。经试算,对普通矩形钢管混凝土,可近似按θ=-0.063(h/b)2+0.762(h/b)-0.426 rad进行计算。对带约束拉杆矩形钢管混凝土,由于截面参数众多而试件数相对较少,统一取θ=0.35 rad进行计算。

图5所示为表1中9个试件轴压荷载—纵向应变曲线的计算结果与试验结果的对比,可见两者较为吻合。26个试件的承载力的有限元计算值Nuc与试验值Nue的对比见表1,两者之比的均值为0.995,均方差为0.045,离散性较大可能是试验方法或条件的差异引起的。总的来看,本文建议的混凝土本构关系比较合理,可供对构件进行有限元分析时使用,并且只需按本文建议的方法对核心混凝土强、弱约束区的划分稍作更改,就可以较容易的扩展到对其他形式的(如设肋等)矩形钢管混凝土柱的分析中。

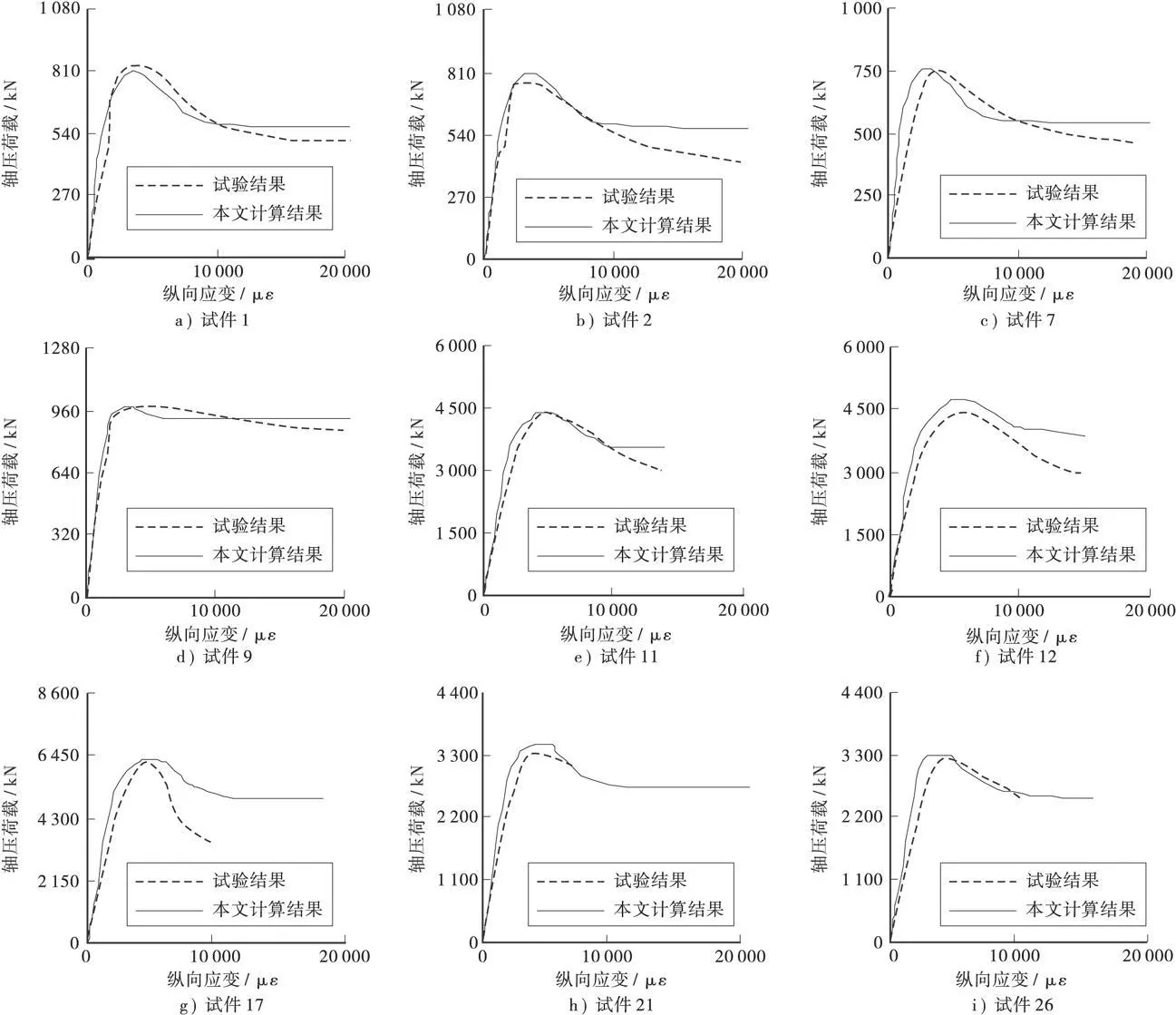
图5 计算结果与试验结果对比

3 结论

1)提出了基于体积的核心混凝土强、弱约束区的划分,符合普通矩形及带约束拉杆矩形钢管混凝土柱的约束机理和整体上的变形趋势,同时改进了Mander约束混凝土模型中有效侧向约束系数的计算方法。该方法力学概念清晰且易于扩展。

2)借鉴了Mander约束混凝土模型的建立思路,根据矩形钢管混凝土轴压试验结果对其中的极限强度、峰值应变及下降段进行修正,建立了可供对普通矩形或带约束拉杆矩形钢管混凝土构件进行ABAQUS有限元分析的统一的核心混凝土本构关系。

3)本文对普通矩形及带约束拉杆矩形钢管混凝土试验结果的验算表明,在建立适用于ABAQUS分析时的核心混凝土本构关系时,应考虑其强度和延性(峰值应变及下降段)的增加。

[1]韩林海.钢管混凝土结构——理论与实践(第二版)[M].北京:科学出版社,2007.

[2]Stephen P.Schneider.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering,1998,24(10):1125-1138.

[3]Da-lin Liu,Wie-Min Gho.Axial load behavior ofhigh-strength rectangular concrete-filled steel tubular stub columns[J].Thin-walled Structures,2005,43():1131-1142.

[4]蔡 健,何振强,陈 星.带约束拉杆矩形钢管混凝土短柱轴压性能的试验[J].工业建筑,2007,37(3):75-80.

[5]李学平.矩形钢管混凝土柱的基本力学性能研究[D].上海:同济大学,2004.

[6]Qingquan Liang,Brain Uy,J.Y.Richard Liew.Nonlinear analysisof concrete-filled thin-walled steel box columns with local buckling effect[J].Journal of Constructional SteelResearch,2006,62(6):581-591.

[7]蔡 健,龙跃凌.带约束拉杆矩形钢管混凝土的本构关系[J].工程力学,2008,25(2):137-143.

[8]陈 曦.带约束拉杆矩形钢管混凝土轴压受力性能研究[D].上海:同济大学,2008.

[9]Ehab Ellobody,Ben Young.Nonlinearanalysisof concrete-filled steel SHSand RHScolumns[J].Thin-walled Structures,2006,44(8):919-930.

[10]Mander J B,Priestley M JN,Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,ASCE,1988,114(8):1807-1826.

[11]蔡 健,孙 刚.带约束拉杆L形截面钢管混凝土的本构关系[J].工程力学,2008,25(10):173-179.

[12]蔡 健,何振强.带约束拉杆方形钢管混凝土的本构关系[J].工程力学,2006,23(10):145-150.

[13]William K J.Warnke E P.Constitutivemodel for the triaxialbehavior of concrete[C].Proceedings of International Association for Bridge and Structural Engineering,ISMES,Bergamo,Italy,1975.

[14]Susantha K A S,Ge H B,Usam i T.Confinement evaluation of concrete-filled box-shaped steel columns[J].Steel and Composite Structures,2001,1(3):313-328.