基于MPPMSG及混合式3L变流器的新型风电变换系统的设计和比较
曾翔君,张宏韬,李 迎,房鲁光
(西安交通大学电气工程学院,西安 710049)
1 引言
MW级以上的风电机组是当前风力发电技术的主流,目前单机功率已经达到5 MW,并进一步向更高的等级发展,以适应未来海上风电的要求。直驱风电机组方案(EESG DD和PMSG DD)由于不需要变速箱,可大大提高系统的效率,并缩短故障平均维护时间(MTTR),改善其可靠性[1-2]。但是直驱方案需要全功率电力电子变流器实现风机的变速控制。由于风力发电机的常规电压等级仅为690 V(或960 V),这使得全功率变流器必须处理比较大的电流,不仅造成滤波电抗等无源元件的体积庞大,另外也引起效率的问题非常突出。为了降低功率半导体器件和无源元件的开销,常规的解决方案是采用传统的两电平变流器并联来分摊容量,但这是一种效率不高的做法。最近的一些研究已经表明,多电平变流器不仅拥有比两电平变流器更优越的谐波性能,而且还具有更高的效率[3-4]。因此在风力发电的低压系统中采用多电平变流器成为当前的一个研究热点。由于多电平变流器的拓扑结构比较复杂,需要的半导体器件较多,因此直接应用于低压系统其成本开销很大。另外,在低压大电流的场合下,多电平变流器的直流母线电容存在较大的电压波动,而且还需要进行电容电压的平衡控制,特别是在风电系统中,强风或者湍流等瞬变风能的影响对于电容电压的平衡控制是很不利的。本文提出一种基于多相永磁同步发电机和三电平混合式全功率变流器的直驱风电系统的技术方案。这种方案通过三电平变流器串联和并联组合替代常规的两电平变流器并联方案。串联组合可以提高直流母线电压等级使三电平逆变器工作于中压范围,而并联组合则能够克服三电平变流器电容中点电压脉动,同时最重要的是利用这种方案可以实现很高的效率。本文将详细讨论这种技术方案的拓扑结构、参数设计以及电容平衡控制等关键性问题,最后对其效率与传统两电平变流器并联方案进行了比较。
2 基于多相永磁同步发电机和三电平混合式全功率back-to-back变流器的风电系统结构
图1a给出了常规的采用永磁同步发电机和并联两电平back-to-back变流器的直驱风电系统原理示意图。图1b给出了本文推荐的基于多相永磁同步发电机和三电平混合式back-to-back变流器的系统结构示意图。图中还给出了两电平(2L)和三电平变流器一个支路的拓扑结构原理图,其中包括Vienna整流器和中心点二极管箝位逆变器 (3LNPC)。比较图1a和图1b可见,本文推荐的方案具有以下几个特点:(1)直接通过永磁同步发电机多相绕组设计产生多组隔离三相电源,不仅可以简化变流器的并联,也能够实现变流器的串联。在图1b的方案中,通过直接利用发电机的定子漏抗,多相并联的变流器不需要Boost电感,与图1a的方案相比,这可以大大降低无源元件的成本和体积,提高系统的效率。(2)发电机被设计成6相,每相包括一对空间相差180°的反向绕组 (在图1b中分别标注为 0°和 180°以及 30°和 210°)。 反向绕组被用于两个三电平VIENNA整流器的并联,用以消除或削弱其直流母线电容中点的电压波动。(3)直流母线电压通过VIENNA整流器串联提高到中压范围,逆变器部分采用两组并联的3L-NPC逆变器。与图1a的方案相比,提高母线电压可以充分利用三电平变流器在中压范围的应用优势,一方面降低输出变流器的电流等级,另一方面也能简化并网滤波器的设计。从输出容量上考虑,一组中压3L变流器相当于两组低压2L变流器的并联。
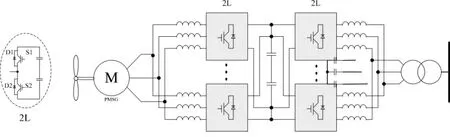
图1a 常规三相PMSG和两电平变流器并联风电技术方案

图1b 多相PMSG和三电平混合式变流器风电技术方案
3 2.5 MW 6相12绕组直驱永磁同步发电机的结构及变流器元件的选择
为了对图1a和图1b两种技术方案进行比较,本文针对一个2.5 MW的风电系统开展研究。图2给出了本文设计的一个功率等级为2.5 MW,电压等级为690 V的6相12绕组直驱永磁同步发电机的结构示意图和电势星形图。在总体结构上,该电机为6相凸极径向式永磁同步电机,但是在每相绕组的定子槽内均安装了两套绕组。电机永磁体材料采用钕铁硼(Br=1.3 T,Hc=987 kA/m),电机极对数p=20,总槽数Q=288,每极每相槽数q=1.2,单元电机数t=4,单元电机槽数Z0=72,单元电机极对数p0=5,绕组循环数:2-1-1-1-1。
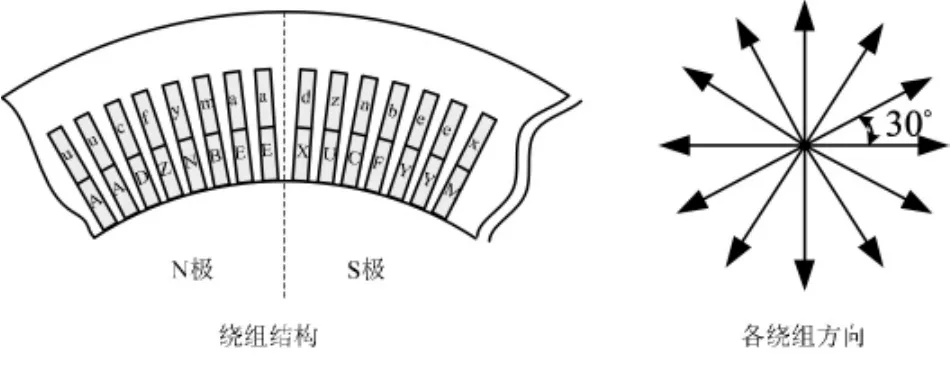
图2 2.5 MW 6相12绕组直驱永磁同步发电机的绕组结构
图2 只画出了一对极。图中A-a,B-b,C-c与D-d,E-e,F-f分别为电角度相差120°的三相绕组,这两个三相绕组之间则相差30°。同理X-x,Y-y,Z-z与U-u,M-m,N-n为相差120°的三相绕组,而两个三相绕组之间也相差 30°。A-a,B-b,C-c与 X-x,Y-y,Z-z 为两个相差 180°的绕组;D-d,E-e,F-f与U-u,M-m,N-n 也相差 180°。限于本文的篇幅,关于该电机的详细设计内容将另文阐述,在此只给出其等效电路参数(见表1)。

表1 2.5 MW 6相12绕组直驱永磁同步发电机的单相参数
如果采用图1a的方案,一个2.5 MW,690 V的直驱风电系统(整流侧和逆变侧)可以采用四组2L变流器并联。这样,每组变流器的相电流仅仅为523 A,最低的直流母线电压1 000 V,可以选择1 700 V/1 200 A的IGBT模块来构成2L变流器。
如果采用图1b所示的3 L混合式方案,发电机侧连接四组Vienna整流器,其中与两组反向绕组相连接的Vienna整流器并联,而并联后的整流器组则串联以获得两倍的直流母线电压。这样,每组Vienna整流器的IGBT和二极管耐压仅为选择2 L整流器时的一半,因此可以选择1 200 V/1 200 A的IGBT模块和FRD模块来构成。电网侧的逆变器虽然承受最低直流母线电压为2 000 V,但是3L-NPC变流器的IGBT和FRD只承压1 000 V,而且由于两组并联,因此IGBT和FRD模块可以选择1 700 V/1 200 A等级。表2给出了图1a和1b两种方案半导体器件和电抗器的数量和等级。
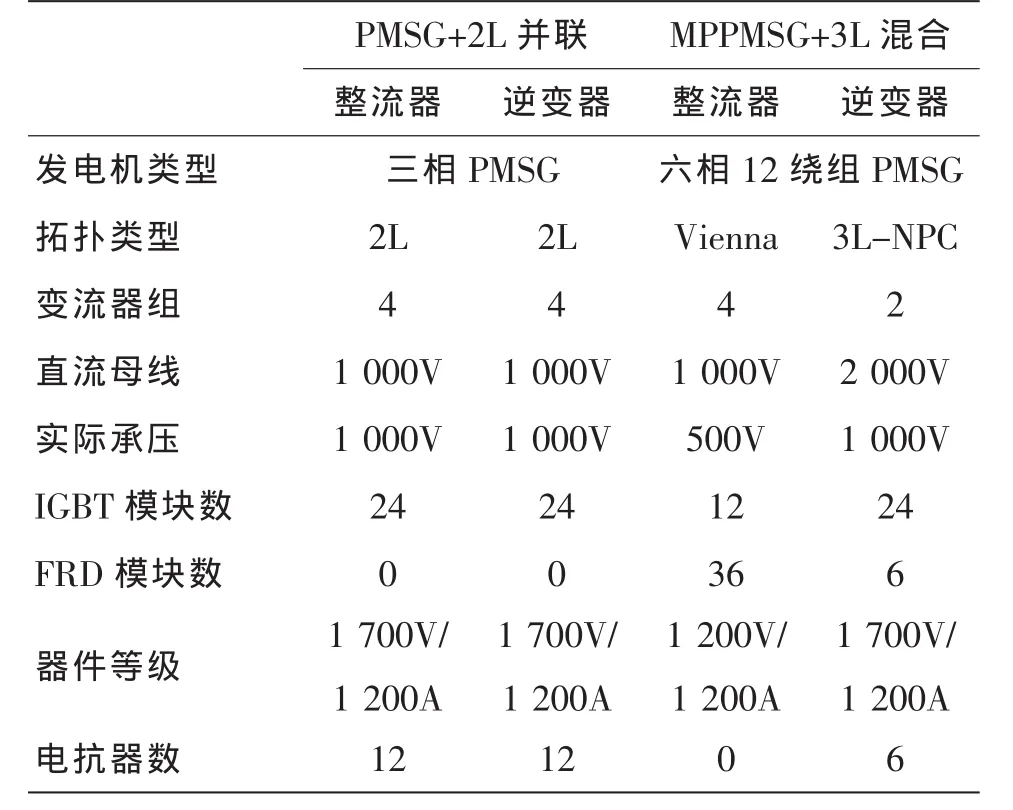
表2 各种拓扑结构IGBT和FRD数量及等级
从表2可知,采用图1b方案可大大降低IGBT模块的数量以及电抗器的数量,因此对于降低系统成本和提高效率具有重要意义。
4 变流器的调制方式以及电容电压平衡控制
对于图1b所示的基于多相永磁同步发电机和三电平混合式的直驱风电系统,实现变速控制的一种简单的方法即由发电机侧的Vienna整流器控制直流母线电压的稳定,从而实现串联的均压。在这种控制方式下,Vienna整流器工作于cosγ=1模式,即发电机出口电压和电流的功率因数为1。电网侧3L-NPC逆变器通过控制注入电网的有功电流间接实现风机的变速控制。虽然采用这种策略进行风机的变速控制其响应速度比较慢(中间大电容直流环节的影响),但是在实现上却非常简单。
变流器的性能与其采用的调制方式具有很大的关系。由于SVM能够实现较高的直流母线电压利用率和优良的谐波性能,因此本文选择SVM调制方式。关于2L变流器的SVM调制技术,文献[5]中已经给出了详细的介绍,并且将其与其它调制方式进行了综合比较。文献[6-7]中对Vienna和3LNPC变流器的标准SVM调制方式进行了阐述,Vienna变流器本质上是单极性的3L-NPC变流器,因此两种变流器调制方法非常相似。
Vienna整流器和3L-NPC变流器存在一个重要的问题是如何维持电容电压的平衡。这里不平衡的原因来自两个方面:一是SVM调制引入的“中间矢量”造成电容电压周期波动或失衡;二是变流器不理想的开关特性,如IGBT导通压降的差异,占空比的有限分辨率等引起电容电压缓慢漂移。许多文献中都提出了各种解决这种不平衡问题的方法,例如通过检测电容电压的偏离,或者在调制信号中注入一个直流分量,或者通过另外一个变流器注入电流来抵消或者抑制偏离[8]。在风电系统中,风速的随机波动、强风突袭、湍流等扰动因素对于3L变流器的电容平衡控制会造成重要的影响。因此,基于SVM调制的On-off控制策略是一种非常适合风电变流器的电容电压平衡控制方法。下面以3L-NPC为例来说明On-off策略的原理。
根据文献 [7]中提出的3L-NPC变流器标准SVM调制方法,在每个开关周期内选择的7个开关矢量序列中都会包含一个中心矢量Vx(x=1-6)及它的冗余矢量V'x(x=1-6)。这两个矢量对直流母线电容中点注入的电流方向刚好相反。在理想情况下,分配给两个矢量的占空比是相等的,因此注入电容中点的电流刚好互相抵消。但是为了平衡电容中点电压的偏离,可以有效控制两个矢量的占空比使其不相同,进而产生一个直流偏移来抑制电压失衡。On-off控制策略的思想是根据电容电压的偏离方向,只选择中心矢量Vx或者V'x中的一个来抵消偏离。可见,On-off控制是一个实现简单、控制响应速度快、而且不存在稳定性问题的方法。图3给出了本文提出的一种On-off控制的实现框图。
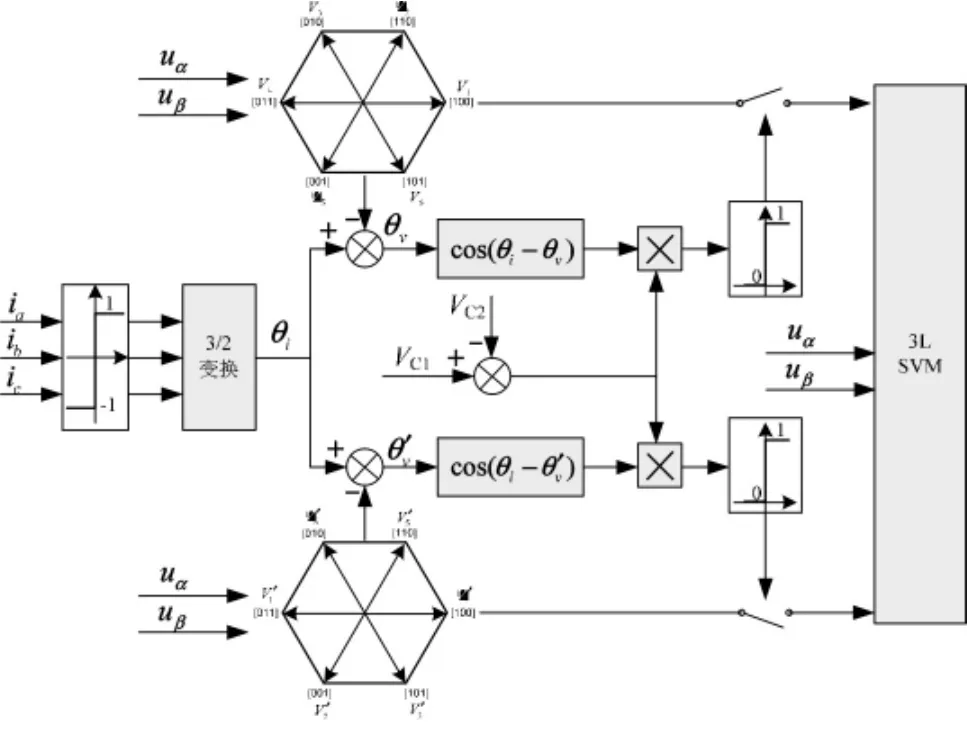
图3 3L-NPC电容中点平衡控制的On-off控制方法原理图
如图3所示,uα,uβ为输入调制器的控制信号,VC1-VC2为直流母线电容中点的电压偏差。θv,θ'v为SVM矢量图中6个中心矢量Vx(及其冗余矢量V'x)中与 uα,uβ对应的那个矢量在静止坐标轴 (α-β)上的相角,其中 θ'v=180+θv。 θi为三相电流的极性构成的矢量,经过3/2变换后在静止坐标轴上的相角。
5 变流器的电容电压脉动及其抑制
2L和3L变流器中的直流电容 (即2L和3LNPC的直流母线电容,3L-FLC的飞跨电容)是重要的无源元件。大的直流电容能够减小电容电压的脉动,进而改善变流器的谐波性能,但是过大的电容不仅增加变流器的体积和成本,同时在图1b的方案中,过大的直流母线电容对于发电机变速控制的响应速度会带来不利影响。
5.1 2L变流器直流电容的电压脉动
2L变流器的直流电容电压脉动受到相电流、调制度、负载功率因数以及开关频率等众多因素的影响。采用一般意义的平均值的方法,即假设在一个开关周期内,相电流保持恒定,可以对流入直流电容的电流i¯cap进行积分来计算电压脉动,即,式中q为占空比,k(t)反映了单位电容上瞬时电压波动(归一化值)。k(t)的最大值K代表了最大电压脉动。图4描绘了各种调制度和负载相角条件下,2L直流电容上的电压脉动系数K(无量纲)。

图4 直流电压脉动系数K与调制度及相角的关系
实际电路中的电压脉动可以通过下式来计算:

式中:Iph,peak表示相电流峰值;fsw表示开关频率;而CDC表示实际选择的直流电容。
5.2 Vienna和3L-NPC中直流电容的电压脉动
采用SVM调制技术的二极管箝位三电平变流器(Vienna和3L-NPC),其电容中点的脉动电压呈现出三倍基波频率,且脉动幅值与相电流的大小、调制度以及负载相角有关,但是却不受开关频率的影响。采用一般意义平均值方法,3L-NPC的电容中点的电压脉动峰值也可以通过一个归一化的常数Qnorm-max来表征,这里的Qnorm-max具有电量的单位(C)。图5给出了不同调制度和相角条件下的Qnorm-max。实际的电压脉动可以通过公式(2)来计算:

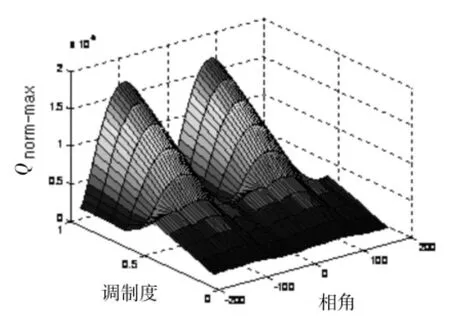
图5 3L-NPC最大电压脉动与调制度及负载相角的关系
Vienna整流器是一个单极性的3L-NPC,它的工作区域仅仅局限在1,4象限,相电流和相电压之间最大允许30°的相差,而且允许相差还取决于调制度的大小。图6a的阴影部分给出了Vienna的工作区域。图中,当调制度m在取值范围(0,0.577)内时,相差的范围为(-30°,30°);而当调制度 m 在范围(0.577,1)内时,调制度m与最大相差γ满足边界条件:

可见,为了最大化利用直流母线电压,Vienna整流器只能工作于γ=0,即进行功率因数为1的控制。在γ=0的条件下,Vienna整流器的电容中点电压脉动峰值(归一化值Qnorm-max)与调制度的关系绘制于图6b中(图中阴影部分的包络线)。

图6 Vienna整流器的工作特性
图5 和图6给出的脉动电压关系是在理想情况下不进行On-off电压平衡控制的稳态结果。如果考虑On-off控制,那么脉动电压峰值会低一些。尽管如此,Vienna和3L-NPC电容中点电压脉动不能通过提高开关频率来抑制。不过,在低压大电流的情况下,这个三倍基波频率的电压脉动可以通过变流器反相并联来抵消。变流器并联不仅能够分摊整个系统的容量,降低相电流的幅值,同时如果两组并联变流器的相电流相位相反,那么这个脉动就可以被自动削弱,甚至消除。图7给出了理想情况下3L-NPC逆变器并联消除电容中点脉动电压的仿真波形。其中,图7a给出了单组逆变器的相电流和电容中点电压脉动的波形图;而图7b给出了两组反相逆变器并联后的相电流和电容中点电压。
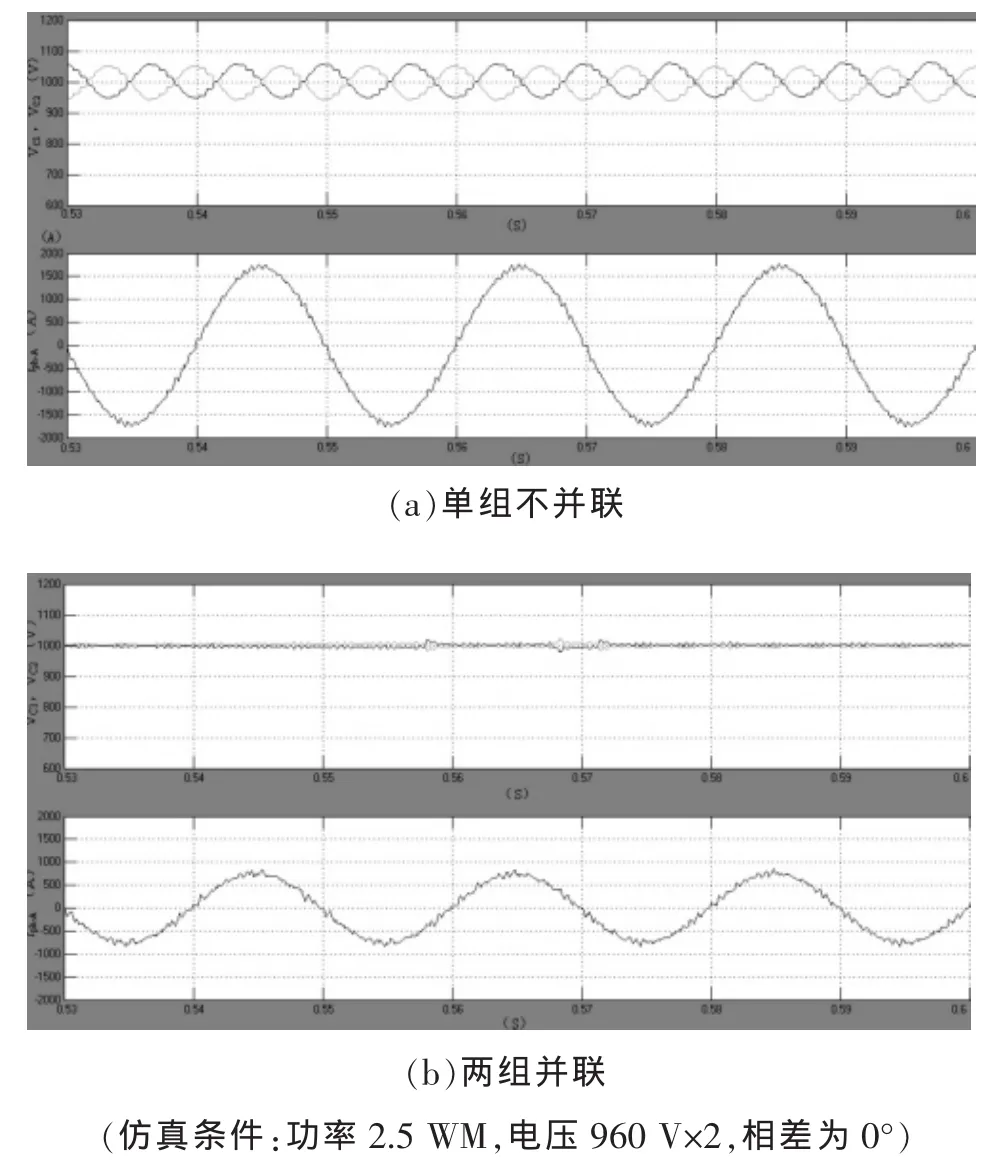
图7 3L-NPC逆变器的相电流与电容中点电压脉动仿真波形
6 电网侧LC滤波器设计
并网的风电变流器必须满足严格的电力系统谐波标准IEEE519-1999,为此LC滤波器通常被用于滤除开关频率附近及其倍数次的谐波。在大功率低压风电系统中,LC滤波器的体积和成本在整个变流器中的比重比较大。另外,大电流的应用场合,滤波电抗上的基波压降也是一个不能忽视的问题,因为它将使变流器的直流母线电压被升高。与图1a方案相比,采用图1b方案能够使得滤波电感的数量大大降低,同时3L变流器还具有更优越的谐波性能。
表3 中给出了不同的调制度下2L和3L变流器输出PWM波的电压谐波THD的比较以及WTHD的比较,这里WTHD代表电压谐波作用在电感负载上产生的电流谐波。WTHD定义为:,式中V1为基波幅值,而n则表示谐波次数。从表3中的数据可以看到,3L变流器PWM波的电压谐波仅为2L变流器的50%,无论是否采用On-off平衡控制;但WTHD值则受到电容平衡控制的影响,除了调制度特别低的情况(如表中的0.4),其它调制度下,采用On-off平衡控制策略的Vienna和3L-NPC的WTHD相当于2L的大约70%,而不采用On-off控制的理想SVPWM波的WTHD则是2L的50%。产生这种不同的原因是On-off控制引起开关频率以下的分数次谐波。

表3 不同调制度下2L和3L变流器的谐波比较
图8 分别给出了2L和3L变流器在同样调制度和负载功率因数条件下相电流的仿真波形及其谐波THD。从仿真波形可以清楚的看到On-off电容电压平衡控制对于电流谐波的影响。滤波电感参数主要根据流过电感的电流谐波的要求来进行设计。公式(4)给出了直流母线电压Vdc、滤波电感Lf、开关频率fsw和调制度Mi与流过电感的电流谐波Ih之间的关系[5]。

公式(4)中额外乘了一个谐波系数h,该系数用于考虑不同变流器拓扑对电流谐波的影响。如表3所示,对于2L,h=1;具有On-off电容平衡控制的Vienna和 3L-NPC,h=0.7;理想 3L 变流器,h=0.5。
滤波电容通过LC滤波器的谐振频率fres的配置来决定。通常fres选择在开关频率fsw的1/2处。LC滤波器的谐振频率的表达式见公式(6)。
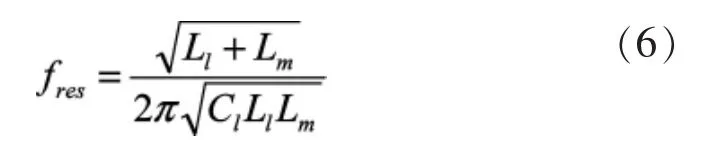
上式中,Lm是升压变压器的漏感以及电网的短路电抗折算到变压器低压侧的等效值,它与LC滤波器构成LCL结构,其谐振频率按照该公式(6)来计算。
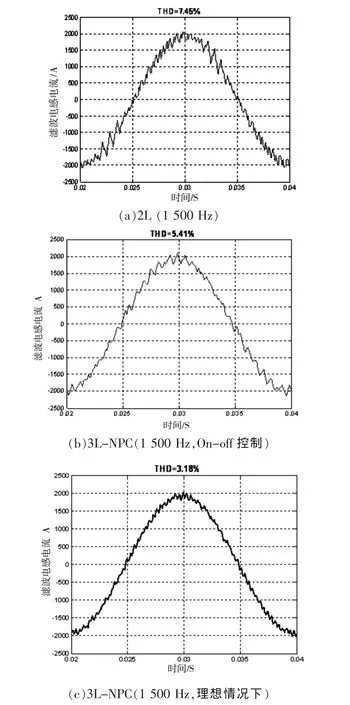
图8 不同变流器的相电流仿真波形和谐波比较(m=0.8)
7 不同变流器拓扑的损耗分析
本节将对图1a和图1b两种技术方案应用于2.5 MW的风电系统中的变流器的损耗问题进行分析。根据表2中给出的半导体器件的等级,Vienna变流器选择商用IGBT模块FZ1200R12KL4C和同等级的FRD为分析对象;2L,3L-NPC以及3L-FLC选择IGBT模块FZ1200R17KE3以及同等级的FRD为分析对象。通过理想开关电路模型结合实际器件的损耗曲线可以建立不同变流器拓扑的损耗模型。选择125℃的IGBT和FRD损耗特性曲线,不同变流器拓扑的损耗分布如图9a和9b所示。从图9a可以看到,整流器中主要的损耗是由二极管产生的。Vienna整流器的四个箝位二极管Dn1~Dn4(如图1b)没有反向恢复损耗,但是其通态损耗在整个变流器的总损耗中占有很高的比例,因此在实际中Dn1~Dn4应该选择低通态压降的整流二极管,而不是快恢复二极管。

图9 不同变流器的损耗分布比较(额定功率2.5 MW)
从图9b可以看到,当功率因数PF=1时,逆变器中IGBT损耗所占比重最高,二极管损耗则较低。相比之下,3L-NPC的损耗远低于2L逆变器。
图10 比较了不同的输入功率和开关频率下,2L和Vienna整流器以及2L和3L-NPC逆变器的损耗变化曲线。可见,三电平混合式变流器比同样容量下并联两电平变流器拥有更高的效率,损耗几乎可以降低50%。随着功率的提高,这种效应也更加明显。另外,2L变流器的损耗特性与开关频率的关系更大,即随着开关频率的提高,2L变流器的损耗增加的更快。这说明2L变流器不能工作在较高的开关频率下。既然提高开关频率可以有效降低LC滤波器的体积和成本,故3L变流器拥有2L变流器无法比拟的优势。

图10 不同变流器损耗的比较
8 结论
通过本文的分析、设计和比较,在大功率直驱风电系统中采用多相永磁同步发电机和三电平混合式全功率变流器可以实现高效率的电能变换。与传统的三相发电机和两电平并联全功率变流器方案相比较,其半导体器件损耗可以降低50%,而由于滤波电抗的数目也大大减少,故滤波电抗的损耗也能大大降低。因此,随着风机功率等级的不断提高,三电平混合式变流器替代两电平变流器并联将是非常有前景的应用方式。
[1]Tavnet P J,Van Bussel G J W,Spinato F.Machine and Converter Reliabilities in Wind Turbines[C].The 3rd IET International Conference on Power Electronics,Machines and Drives,Dublin,Ireland,Mar,2006.pp.127~130.
[2] Deok-je Bang,Henk Po Under,Shrestha G,et al.Promising Direct-Drive Generator System for Large Wind Turbines(C).EPE-WECS 2008,Delft,Netherlands,Mar,2008.pp.1-10.
[3] Ralph Teichmann,Mariusz Malinowski.Evaluation of Three-Level Rectifiers for Low -Voltage Utility Applications[J].IEEE Transactions On Industrial Electronics,2005,52(2):471-481.
[4]Zeng X J,Chen Z,Blaabjerg F.Design and Comparison of Full-size Converters for Large Variable-Speed Wind.Turbines[C].The 12th European Confer ence on Power Electronics and Applications,Aalborg,Denmark,2007.
[5]Hava A M,Kerkman R J,Lipo T A.Simple analytical and graphical methods for carrier-based PWM-VSI drives[J].Power Electronics,IEEE Transactions on,Volume 14,Issue 1,Jan.1999 Page(s):49-61.
[6]Grzegorz Radomski.Voltage Space Vector Control System ofVienna RectifierI [C].IEEE The International Conference on Computer as a Tool,Warsaw,Poland,2007,1666~1673.
[7]Beig A R,Narayanan G,Ranganathan V T.Space Vector Based Synchronized PW M Algorithm for Three Level Voltage Source Inverters:Principles and Application to V/f Drives[C].IEEE Industrial Electronics Conference,Sevilla,Spain,2002,1249-1254.
[8]Yazdani A,Iravani R.A Generalized State-Space Averaged Model of the Three-Level NPC Converter for Systematic DC-Voltage-Balancer and Current-Controller Design[J].IEEE Transactions on Power Delivery,2005,20(2):1105-1114.

