一种新颖的正弦正交编码器细分方法

洪小圆，王鹿军 吕征宇

（浙江大学电力电子国家专业实验室，杭州 310027）

1 引言

随着社会的发展，人们对电梯的体积、载重量、功耗、调速精度及调速范围等提出了越来越高的要求，永磁同步电机以功率密度大、气隙密度高、转矩电流比高、转矩惯量比大、寿命长及结构简单等优点成为无齿轮曳引机的首选[1]。对于正弦波永磁同步电机矢量控制系统，坐标变换中的转子位置角是否能准确、实时地检测，直接影响到整个系统的性能，因此高性能要求的系统一般采用分辨率高的光电式编码器检测转子位置[2]。文献[3]对方波增量编码器与正弦波增量编码器的测速方法做了归纳比较，在数字测速仪应用中，双边沿并行采样计算的固定时间检测法(PEM-CSDT)误差最小，带补偿的正弦编码器细分测速方法次之；而在低速闭环控制系统中，通过正弦编码器相位检测得到的速度反馈延迟最小，带宽可以做得比采用其他测速方法大，速度误差最小，在无齿轮电梯场合中得到广泛的应用。正弦编码器的细分有多种方法，文献[4～6]提出了tan-1的查表法，文献[7]提出了sin-1的查表法，文献[8]提出了高阶倍频的查表法，这三种细分方法都是以在线采样的编码信号幅度为索引，到离线制作的表格里寻找对应的相位，细分分辨率越高，所需A/D转换器的精度就越高，存储表格的空间就越大。为了节省存储空间，文献[9～10]提出了径向基神经网络插补法，但是算法复杂；文献[11]提出了基于sin-1的近似计算法，但是涉及到多次的乘法及除法运算，细分误差越小，乘法运算次数越多，相位检测时间越长；文献[12～13]提出了多段准线性近似法，虽然不需要复杂的运算，但是细分误差越小，分割的段数就要越多，模拟实现需要大量的器件，数字实现则需要占用大量的程序空间。

本文提出了一种不用查询表的正弦正交编码器细分方法，根据控制系统临界稳定原理生成与正弦编码信号等幅值的高频正弦载波，同时采用定时器生成一个与载波相位对应的锯齿波，将高频载波与正弦编码信号比较，当两者相等时保存锯齿波幅度即可获得正弦编码信号的相位。与传统查询表细分方法相比，节省了大量的存储空间，且不需要添加额外的硬件，载波、锯齿波的生成及相位检测过程全部由软件实现，算法简单，尤其适用于低速运行及静止时的位置检测。

2 正弦增量信号细分原理

正弦增量式编码器每转输出Nenc个增量sin/cos信号，Nenc为编码器的线数，编码信号输出并非完全正弦，存在直流偏置、相位偏差等非理想因素，影响细分的精度，校正方法已见诸多篇文献 [14～15]，本文不再赘述，下文的分析建立在编码信号理想正弦的基础上，sin信号与cos信号幅值相等，相位相差90°，则两路正交信号可表示如下：

式中：A为信号幅值；ωm为电机转子角速度；ω1为信号角频率。如果两个幅值相同而频率不同的正弦波在某一时刻幅度相等，只要知道其中一个正弦波的相位，就可得到另一个正弦波当前的相位。本文利用已知相位的高频正弦载波与正弦增量信号比较来获取每个正弦增量周期中的具体相位，从而实现细分。用于提取相位信息的高频载波表示如下：

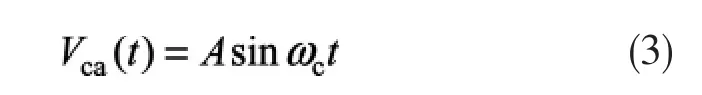
式中ωc为载波角频率，载波幅值与正弦增量信号幅值相等。载波信号与sin信号分别作为比较器的正负输入，比较器输出如图1(b)所示，每个载波周期中，Va（t）与 Vca（t）相交于两点，只保存比较输出下降沿时刻的相位，如在 t0时刻，Va（t0）=Vca（t0），载波此时的相位可从图1(c)中的相位锯齿波里查到为θc=α，则正弦增量信号相位θa=θc=α。依次求出每个载波周期交点对应的相位即可求出Va（t）整个周期范围内的相位，当载波频率为无限大时，θa的轨迹可近似为图1(d)中所示的分段直线（虚线），单纯在下降沿保存相位只能保证检测到的正弦增量信号的相位在每个90°范围内为线性，改变θa在90°～270°区间的相位检测时刻为比较输出上升沿即可获得360°范围内线性变化的相位，如图1(d)中实线所示。

本文提出的相位检测方法是基于载波与正弦编码信号幅度的比较实现的，信号幅度的准确性决定了相位检测的准确性，正弦编码器信号离散化后的准确性取决于A/D转换器的精度，由于在波峰与波谷值幅度变化缓慢，因此相位检测畸变较大。为提高系统的性能，必须采取措施进行校正。鉴于编码信号为sin/cos信号，在sin信号到达波峰或波谷附近时，cos信号处于过零点附近，而当cos信号到达波峰或波谷附近时，sin信号处于过零点附近，因此结合使用sin信号与cos信号可以减小离散化造成的相位检测的畸变。每个正弦周期中，sin信号与cos信号在 45°，135°，225°，315°的幅度绝对值相等，以这几个点为分界来分配信号选择区间，如图2所示，加粗线为各区间所采用的信号。使用cos信号检测相位的原理与使用sin信号相同，只是各自对应的载波不同，cos信号对应的载波为：

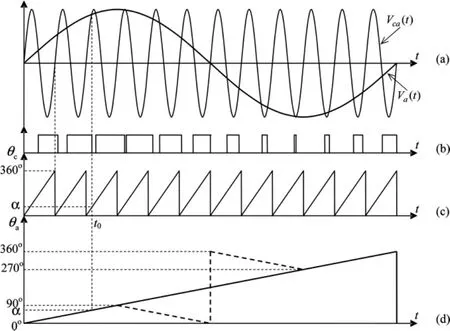
图1 细分原理图

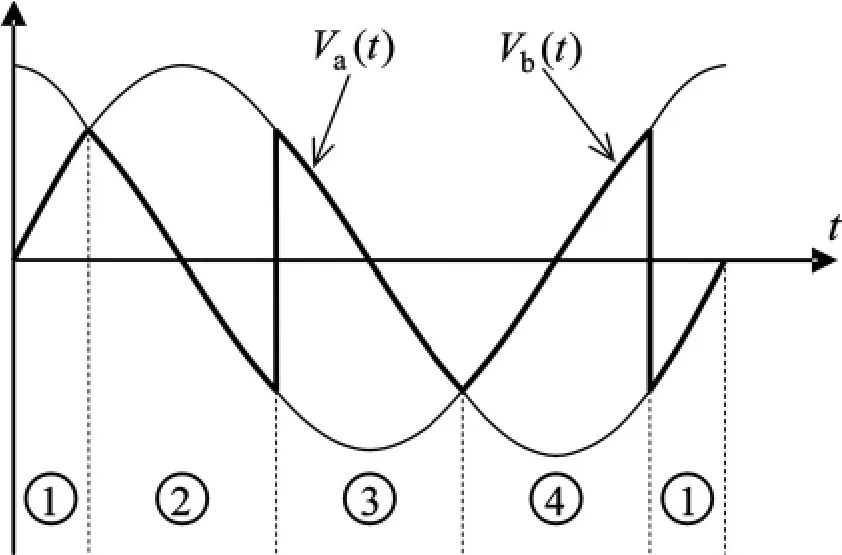
图2 区间分配

表1 区间判据及信号选择

由于编码信号为两路正交信号，通过Va（t）和Vb（t）的值可实时判断θa所处区间，确定区间后即可获得相位检测所需信号及检测时刻，上述一周期内的选择依据归纳如表1所示。

3 载波生成原理

由经典控制理论可知，线性系统特征方程式的根中有一对共轭虚根，而其他的根都在s平面的左半平面时，系统处于临界稳定状态，此时系统的单位冲激响应输出含有等幅震荡的分量。带一对共轭虚根的最简单的连续系统传递函数为：

此系统的单位冲激响应输出函数为sin（ωct）。本文所需正弦载波信号在DSP里生成，是一个离散信号，表示为：

式中：A为正弦载波幅值；ωc为正弦载波角频率；Tcs为离散信号采样周期，即载波步长。对式(6)进行z变换，得：

则输出用差分方程表示为：

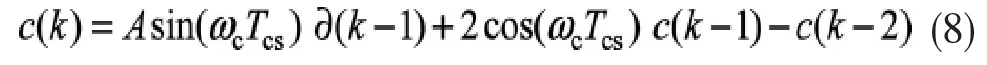
4 反混叠和细分分辨率

图1 为了阐述方便，设定正弦增量信号与载波具有相同的初始相位，实际上两者的初始相位并不一定相等，假设两者初始相位相差φ(0≤φ<2π)，正弦增量信号仍旧用式（1）表示，正弦载波信号表示如下：

本文所提相位检测边沿的选择原则实质上是正弦增量信号与载波信号在此边沿对应的交点处相位相同，可以表示如下：

令ωc=mω1，则检测到的正弦增量信号相位为：

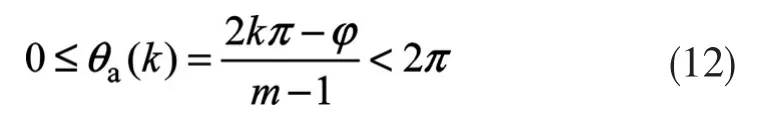
当 φ=0 时，0≤k≤m-2；当 φ＞0 时，1≤k≤m-1。因此不管初始相位如何，一个正弦增量周期中检测到的相位共m-1个，为了保证电机在最高转速下相位细分不产生混叠，一个相位检测周期转过的角度必须小于180°/Nenc，也就是说一个正弦增量周期必须至少检测到2个相位，即m-1＞2，那么满足全速范围内相位细分要求的载波角频率最低要求为：

忽略离散化载波的非线性，正弦增量信号细分分辨率只与m有关系，电机运行于最高转速时，m最小，细分分辨率最低。要提高最低分辨率只能通过提高载波角频率来实现，但是载波角频率ωc受制于离散信号采样周期Tcs和离散正弦载波每周期的点数，用Nc表示，三者关系表示如下：

细分程序嵌入在电机驱动系统里，假设驱动电机的变频器开关周期为Te，每个开关周期内的软件流程包括电流采样、速度计算、坐标转换、PI调节、空间矢量调制以及一些状态位的检测等，共占用时间tctrl，则每开关周期用于编码信号细分的时间最多为Te-tctrl。编码信号细分占用时间包括编码信号采样时间、两个载波信号的生成、相位锯齿波的生成、幅度比较和相位保存，载波信号生成需要两次乘法运算，其余全是逻辑运算，假设每次细分过程占用时间为tscale，则载波步长必须满足下式：

图3 细分系统框图

在整个控制系统方案确定后，可计算出最小载波步长，则影响载波频率的因素只有Nc，Nc决定了离散载波与连续的理想正弦波之间的逼近程度，当电机低速运行时，m变得很大，此时不能忽略离散载波的非线性，Nc成为决定细分分辨率的主要因素，因此通过降低Nc来提高载波角频率会影响到低速时的细分分辨率。综上所述，载波的设计必须权衡系统对高速及低速的性能要求，在无齿轮电梯曳引机驱动场合，低速控制精度是一项主要的性能指标，因此可以选择较大的Nc，并且舍弃高速时的细分，以满足反混叠条件。

5 实验结果

本文在一台无齿轮电梯用永磁同步电机上做了验证性实验，电机具体参数为：10对极、额定转速为350 rpm、额定功率为7 kW。编码器型号：ERN 487-2048(HEIDENHAIN)，输出信号为 A+，A-，B+，B-，R+，R-，C+，C-，D+，D-， 其中 A+，A-，B+，B-为每转 2 048 个 sin/cos信号，C+，C-，D+，D-为每转一个sin/cos信号，R+，R-为零位校正信号。控制芯片为TI公司的TMS320C2812，主频150 MHz，带16通道12位A/D转换器，两个事件管理器 （EVA和EVB），4个通用定时器。

图4 正弦绝对编码信号与相位检测结果

图5 采用增量编码信号与绝对编码信号的转子位置检测

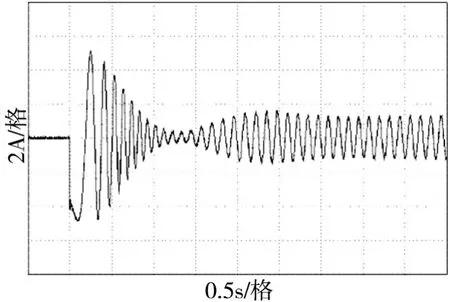
图6 转子初始位置识别后的起动相电流波形

图7 低速时的正弦增量编码信号与载波

ERN487编码器输出的增量、绝对位置信号均是正交正弦信号，通过对增量信号的细分提高速度控制的精度，通过对绝对信号的细分获得转子初始位置，两者可以共用一套载波及锯齿波，细分系统框图如图3所示。图4所示为电机运行于50 rpm时编码器输出的正弦绝对信号以及通过细分正弦绝对编码信号检测到的转子位置，随着电机稳速旋转，转子角度线性递增。为了检验正弦绝对编码信号细分所得相位的准确性，将正弦增量信号整形成方波信号，并通过DSP的正交编码脉冲电路(QEP)进行四倍频及计数，通过QEP计数得到的转子位置分辨率达到1/8192，可以充当转子实际位置，如图5上所示。图5下为绝对编码信号的相位检测结果，上下波形严格平行，对应正弦载波参数为：TCS=2.5 μs，NC=200，ωC=4 000π rad/s， 通过该载波与绝对编码信号比较获得电机初始转子位置后，电机正常起动并稳定运行，起动相电流波形如图6所示。电机运行时通过对增量信号的细分可以提高速度控制精度，图7所示为电机运行于2.5 rpm时正弦增量编码信号与载波波形。

6 结论

本文提出的正弦编码器相位细分方法不需要查询表，节省大量存储空间，且细分过程全由软件实现，细分成本低，适用于低速控制场合，另外，对于编码器带正弦绝对信号的场合，利用该方法可以很好地解决电机转子初始位置识别问题，最后基于7 kW的无齿轮电梯用永磁同步电机的实验结果证明了该方法的可行性。

[1]Wang J H,Tan F W,Jin R L.Research on low-speed gearless permanent magnet synchronous motor for elevator drive[C].Proc.IEEE ICEMS,Nanjing,China,2005.

[2]李崇坚.交流同步电机调速系统[M].北京：科学出版社，2006.

[3]Kavanagh R C.Signal processing techniques for improved digital tachometry[C].Proc.IEEE ISIE,L'Aquila,Italy,2002.

[4]Hagiwara N,Suzuki Y,Murase H.A method of improving the resolution and accuracy of rotary encoders using a code compensationtechnique[J].InstrumentationandMeasurement,IEEE Transactions on,1992,41(1)：98-101.

[5]陈晓荣，陈晓芬，杨甫勤.增量式编码器的相位编码细分研究[J].仪器仪表学报，2007，28(1)：132-135.

[6]史敬灼，王秀丽，徐殿国.交流伺服系统光电编码器信号处理电路设计与实现[J].微特电机，2007，（11）：18-19,55.

[7]Ju-Chan Kim,Jang-Mok Kim,Cheul-U Kim,Cheol Choi.Ultra Precise Position Estimation of Servomotor using Analog Quadrature Encoders[C].Proc.IEEE APEC,Dallas,USA,2006.

[8]Tan K K,Zhou H X,Tong Heng Lee.New interpolation method for quadrature encoder signals[J].Instrumentation and Measurement,IEEE Transactions on,2002,51(5)：1073-1079.

[9]Kok-Zuea Tang,Kok-Kiong Tan,Tong-Heng Lee,Chek-Sing Teo.Neural Network-based Correction and Interpolation of Encoder Signals for Precision Motion Control[C].Proc.IEEE AMC,Kawasaki,Japan,2004.

[10]Kok Kiong Tan,Kok-Zuea Tang.AdaptiveOnline Correction and Interpolation ofQuadrature Encoder Signals Using Radial Basis Functions[J].Control Systems Technology,IEEE Transactions on,2005,13(3)：370-377.

[11]Benammar M.Precise wide-range approximations to arc sine function suitable foranalog implementation in sensors and instrumentation applications[J].Circuit and Systems I,IEEE Transactions on,2005,52(2)：262-270.

[12]Alhamadi M A,Benammar M,Ben-brahim L.Precise method for linearizing sine and cosine signals in resolvers and quadrature encoders applications[C].Proc.IEEE IECON,Busan,Korea,2004.

[13]Benammar M,Ben-brahim L,Alhamadi M A.A Novel ConverterforSinusoidalEncoders [C].Proc.IEEE SENSORS,Daegu,Korea,2006.

[14]Mayer J R R.High-resolution of rotary encoder analog quadrature signals[J].Instrumentation and Measurement,IEEE Transactions on,1994,43(3)：494-498.

[15]Kavanagh R C.Probabilistic learning tech nique for improved accuracy of sinusoidal encoders[J].Industrial Electronics,IEEE Transactions on,2001,48(3)：673-681.