相似理论中时间相似的达成与意义

张 驰 李新东

(郑州铁路职业技术学院,河南 郑州 450052)

1 问题的提出

所谓物理现象相似是指：在单值性条件相似的前提下,两同类物理现象在其空间对应点上的同名物理量的比值是一常数(即对应成比例)。

例如,两相似对流换热过程,其固体壁面对应点上的对流换热系数的比值为一定值,并可由此导出两者的努塞尔数(Nu)必相等[1]。再例如,两相似圆管层流,其对应点上的流速必然成比例,由此可导出两者的雷诺数(Re)必相等。

两物理现象相似的前提,即单值性条件,总共有四个[2]：

(1)几何相似。几何相似是最容易理解的,在实验布局中也最容易实现,这里不再赘述。

(2)边界条件相似。例如两相似流动,在对应边界上均为自有液面,或均为粗糙度相似的固体壁面。边界条件相似的概念也比较容易理解。

(3)物性相似。例如两相似流动对应点上的流体物性,如密度、粘度等物性参数对应成比例。

(4)初始条件相似,即时间相似。对于恒定流或稳态传热过程,则无需该条件,但是对于非恒定流或非稳态传热,则必须保证时间相似。

以上四类单值性条件中的1、2、3都容易理解,各教材也都有详细说明,唯有第4类条件中,对于什么是时间相似,如何实现时间相似,以及时间相似的意义都没有说明。有关论著中的一些说法,比如“速度相似就意味着各相应点的加速度也是相似的”[3],及“所以动力相似是运动相似的保证”[4]等,在没有明确解释时间相似的含义前,这些说法都是难以理解的。这也给很多读者在学习理解相似理论的过程中带来很大的困难。以下,本文将重点讨论时间相似的定义,如何保证时间相似,以及时间相似的意义。

2 时间相似的定义

所谓时间相似是指：在满足几何相似、边界条件相似和物性相似的前提下,若两相似物理现象(例如流动现象)在对应几何点、对应时间点上的同名物理量(例如流体密度、流体速度、加速度、温度、粘度等)对应成比例,则两物理现象中同名物理量对应值成比例时所对应的时间间隔成比例。

3 如何实现时间相似

关于如何实现时间相似,我们看两个流体力学中的实际例子。

3.1 实现时间相似的例子1

建立两相似流动,分别称为原型p和模型m。

(1)满足几何相似、边界条件相似和物性相似。

(2)初始时刻t0,分别在原型和模型按照几何相似选取对应的流体质点n(原型中的点命名为np,模型中为nm,为简明起见,以下用n点代表两对应点)。接下来我们从初始时刻开始,分别追踪质点n在原型和模型中的运动轨迹。

(3)为满足时间相似,做如下工作：分别在原型和模型中分别选择一组对应时刻1、2、3、……、x,连同初始时刻记为 tp0/tm0、tp1/tm1、tp2/tm2、tp3/tm3、……、tpx/tmx(注：p表示原型,m表示模型,以下用法与此相同,不再重复说明),且保证时间比尺Cτ是一常数 ,即

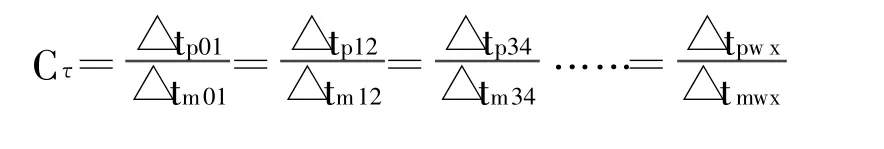
注：△tp01=tp1-tp0,△tm01=tm1-tm0分别为原型和模型的时刻0、1之间的时间间隔,其他依此类推。

注意：这是实现时间相似的关键,即对应时间间隔成比例。

(4)若两流动相似,则对应点(这里即np和nm点)、对应时刻(tp1/tm1、tp2/tm2、tp3/tm3、……、tpx/tmx)的流速必然成比例,即流速比尺Cu是一常数,表示为：

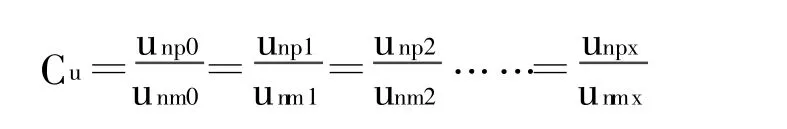
上式中,unp0的角标,n表示n点,p表示原型,0表示时刻0,其他依此类推。

至此,所有的单值性条件(包括时间相似)均达成,且流速相似,即可保证两流动是相似的。

3.2 实现时间相似的例子2

建立两相似流动,分别称为原型p和模型m。(1)满足几何相似、边界条件相似和物性相似。(2)初始时刻t0,分别在原型和模型选择一对应空间点k(原型记为kp,模型记为km,以下为简明起见,用k指两点),其流速分别为ukp0和ukm0。接下来,观察该空间点的流速随时间的变化。

(3)为满足时间相似,做如下工作：

在原型和模型中分别选择一组对应时刻1、2、3、……、x,记为 tp1/tm1、tp2/tm2、tp3/tm3、……、tpx/tm x(注：p表示原型,m表示模型),且保证：

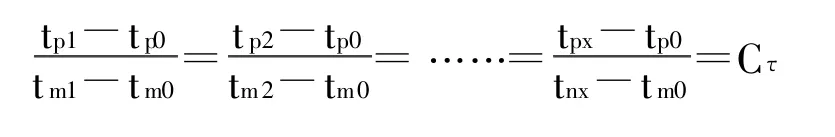
注：上式的角标使用,除k代表空间点k外,其他意义与前文规定相同,不再赘述。

注意：这是实现时间相似的关键,即对应的时间间隔成比例。

(4)若两流动相似,则该空间点(这里即k点)、对应时刻(tp1/tm1、tp2/tm2、tp3/tm3、……、tpx/tm x)的流速必然成比例,即流速比尺是一常数,记为：

至此,所有的单值性条件(包括时间相似)均达成,且流速相似,即可保证两流动是相似的。

4 时间相似的意义

上文我们曾提及“速度相似就意味着各相应点的加速度也是相似的”,这一说法中包含着相似理论的一个重要论断,即按照运动相似建立的两流动,其力学现象也必然相似。这意味着,相似特征可以在不同的物理现象之间,如长度、速度、力之间进行正确的传递,而这正是我们建立相似模型的主要依据。

下面我分别针对上述两个例子讨论,相似特征在不同的物理现象之间传递过程中时间相似的意义。

4.1 针对“时间相似的例子1”的讨论

推论1：例子1中,原型与模型是按照流速相似的原则建立的,可以证明因时间相似,则必然有对应质点的运动轨迹几何相似。

证明：

长度比尺：

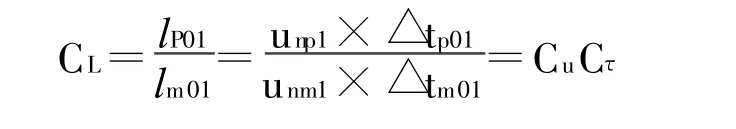
上式中,lp01、lm01分别指流体质点n在对应时间tp0/tm0、tp1/tm1在原型和模型所处空间点之间的连线;unp1的角标含义与前文规定一致,这里近似用时刻1的速度unp1代表原型流动中从时刻0到时刻1质点n的平均速度;△tp12的角标意义与前文规定一致。

类似的还有：

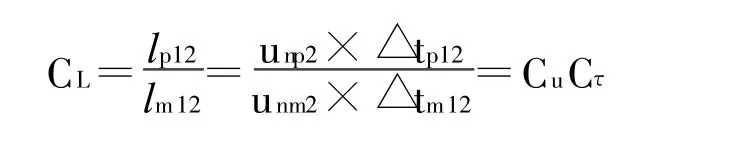
因速度相似速度比尺Cu是一常数,且时间相似时间比尺Cτ是一常数,故长度比尺或几何比尺CL也必然是一常数,故可得到结论,质点n在原型和模型中的运动轨迹必然几何相似。

推论2：例子1中,原型与模型是按照流速相似的原则建立的,可以证明原型与模型对应点、对应时刻的流体加速度相似。

证明：根据流速相似与时间相似,有：

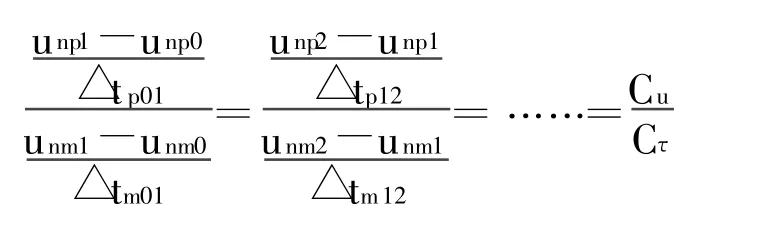
注：上式中角标含义与前文规定一致。

令所有时间间隔趋于0,则上式左端即为流体质点在不同时刻的加速度比尺Ca表示为：

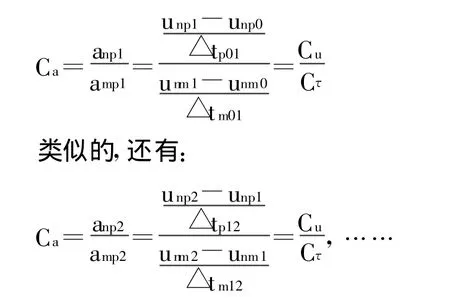
上式中,a表示加速度,角标含义与前文一致。

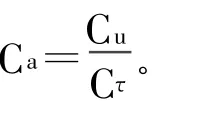
4.2 针对例子2的讨论

例子2中,原型与模型是按照流速相似的原则建立的,可以证明两流动的对应点、对应时刻流体质点的当地加速度相似。

证明：

总结：在本例中再次证明,从运动相似必然可以导出加速度相似,即时间相似是各物理现象(如长度、速度、加速度)相似关系正确传递的主要前提。

5 总结

本文运用举例法阐明了时间相似的具体含义,并指出时间相似是长度比尺、速度比尺、加速度(力)比尺之间正确传递的桥梁,在相似理论中具有重要的意义。

[1]杨世铭,陶文铨编著.传热学[M].北京：高等教育出版社,1998：154-155.

[2]伍悦宾,朱蒙生主编.工程流体力学泵与风机[M].北京：化学工业出版社,2006：94.

[3]周谟仁,主编.流体力学泵与风机[M].北京：中国建筑工业出版社,1979：168.

[4]李玉柱,苑明顺编.流体力学[M].北京：高等教育出版社,1998：304.

[5]章熙民,梅飞鸣,任泽霈,王中铮主编.传热学[M].北京：中国建筑工业出版社,1985.