粗糙集理论在高考信息系统中的应用研究

王路芳, 郭金玲

(1.山西财经大学实验教学中心, 山西 太原 030006; 2.山西大学信息工程系, 山西 太原 030031)

0 前 言

目前，我国每年参加高考的人数越来越多.据教育部统计，2009年全国普通高校招生报名人数约比2008年增加了60万名，高考信息系统也愈加庞大，其包括了各种子系统和各类数据库，如成绩管理、招生管理等，积累了大量的数据.在教育考试领域，随着计算机的普及与发展，越来越多的考试信息使用了计算机进行处理和存放，大大减少了手工处理的工序，减少了存储的空间，提高了存储的安全和便捷性.但是管理人员只能通过简单的统计或排序等功能获得表面的信息，由于缺乏信息意识和技术，隐藏在这些大量数据中的信息一直没有得到应用.如何对这些数据进行重新利用，将现有的管理数据转化为可供使用的知识，提高高中教育管理水平和办学质量，是很多教育部门正在考虑的问题.

1 粗糙集理论在高考信息系统中的应用

1.1 粗糙集理论

粗糙集理论是针对不确定性问题提出的[1，2]，它的特点是不需要预先给定某些特征或属性的数量描述，如统计学中的概率分布，模糊集理论中的隶属函数或隶属度等，而是直接从给定问题的描述集合出发，通过不可分辨关系和不可分辨类确定给定问题的近似域，从而找出该问题的内在规律.其基本思想[3-5]是将数据库中的属性分为条件属性和决策属性，对数据库中的元组根据各个属性的不同的属性值分成相应的子集，然后对条件属性划分的子集与结论属性划分的子集的上下近似关系生成判定规则.

采用粗糙集理论作为知识发现的工具具有很多优点[6].首先，粗糙集理论提供了一套数学方法来从数学上严格的处理数据分类问题，尤其是当数据具有噪音、不完全性或不精确性时；其次，粗糙集仅仅分析隐藏在数据中的事实，并没有校正数据中所表现的不一致性，而是一般将所生成的规则分为确定与可能的规则；第三，粗糙集理论包括了知识的一种形式模型，这种模型将知识定义为不可区分关系的一个集族，就使得知识具有了一种清晰的定义的数学意义，并且可以使用数学方法来分析处理；第四，粗糙集运算可以进行并行运算，适合大规模数据库知识发现的需要；最后，粗糙集不需要关于数据的任何附加信息.

针对以上高考信息系统数据管理过程中的不足，本文将粗糙集理论应用到该系统的数据管理当中[7]，找出影响考生成绩潜在的因素[8,9]，以加强高中教学科学化、规范化管理，提高教学质量和效果[10].

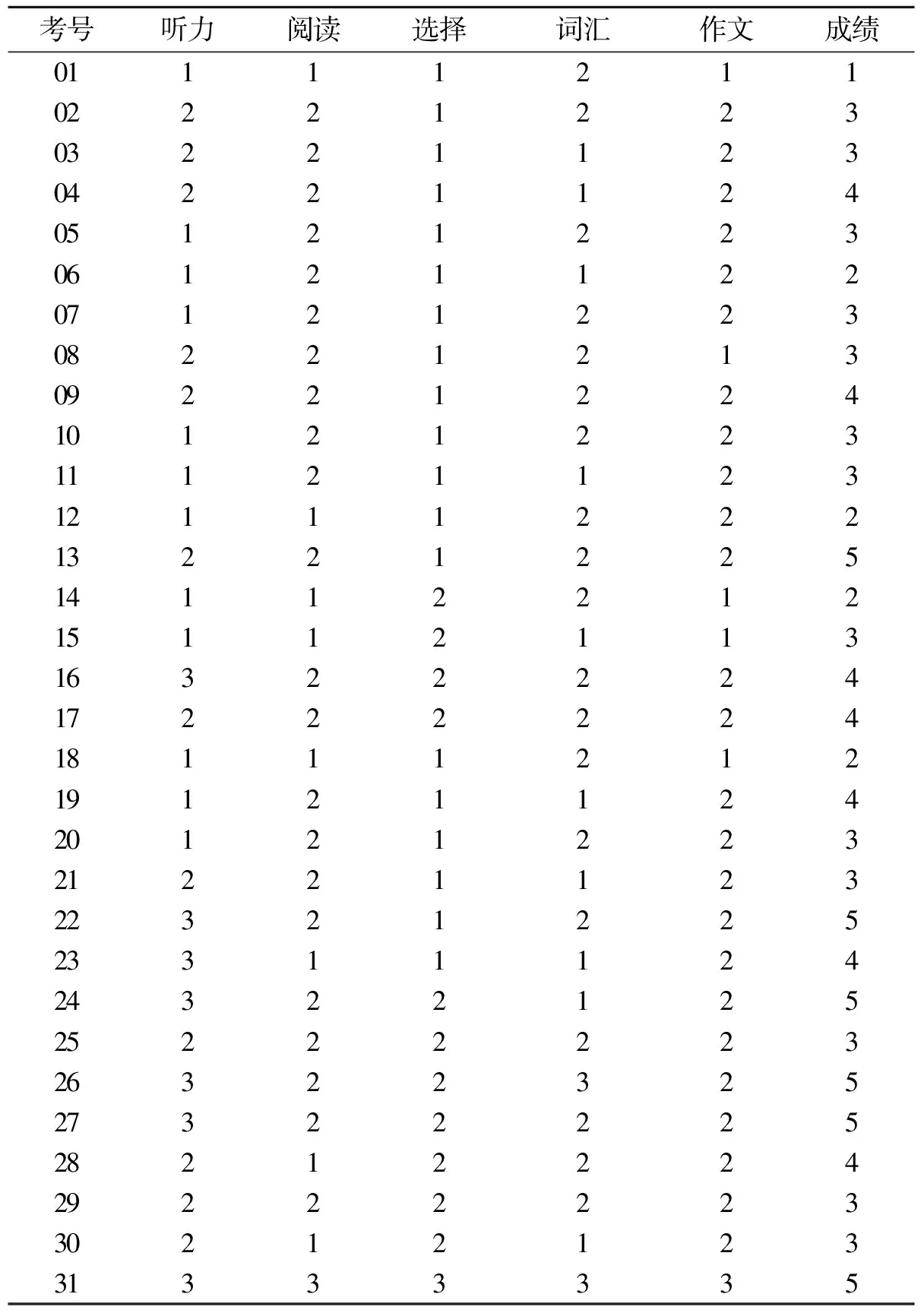
表1 修正数据表

1.2 应用粗糙集理论进行考生成绩分析

利用粗糙集理论中的属性重要性分析方法对山西省2009年高考某高中班学生的英语成绩进行分析.实验数据集来自高考信息系统中的成绩数据库，具体见图1.对这张成绩表进行数据预处理，即采用离散归一化方法把每个大题得分分成3段(排序后从高到低按30%(优良)，40%(中等)，30%(中等以下)分别用1，2，3表示，得表1.

设C表示条件属性集合，由u,v,a,r,t构成，它们分别表示听力、阅读、选择、词汇和作文各条件属性；D表示决策属性，即总成绩.我们将决策属性值取5个值，把全体同学分成成5大类，第一类为优秀的同学(125分以上)，第二类为良好的同学(112～124)，第三类为中等的同学(97～111)，第四类为及格的同学(90～96)，第五类为不及格同学(90分以下)，分别取值为1，2，3，4和5，这样C={u,v,a,r,t},D={1,2,3,4,5}.本实验的目的是分析出条件属性中哪些属性最大程度地改变了决策属性和分类，以此来确定哪些条件属性最重要.为了找出某些属性的重要性，我们的方法是从表中去掉一个属性，再来考察没有该属性后决策分类会发生怎样变化.若去掉该属性，导致分类变化大，则说明该属性的强度大，反之说明该属性的强度小，即重要性小.为方便起见，括号中的数字代表同学的考号，按照各属性进行分类，按D即{1,2,3,4,5}分类如下：记POSc(D)为D的C正域，(D)cγ=POSc(D)/|U|，U为论域.

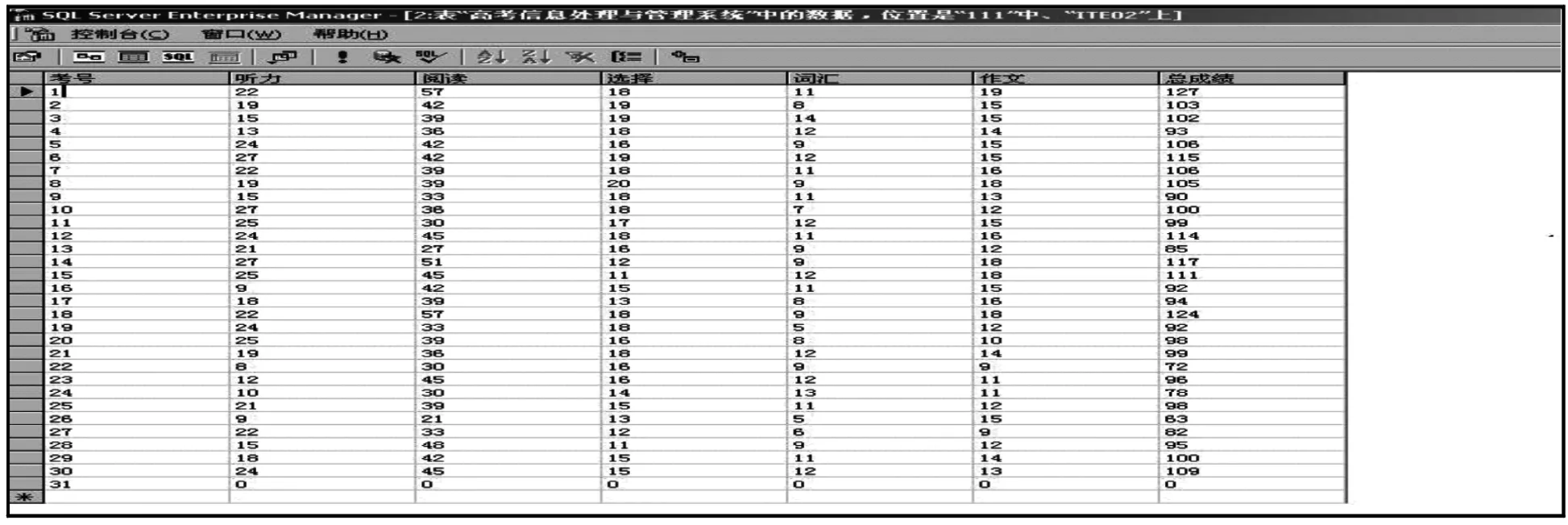
图1 高考成绩数据库中某高中班学生的英语成绩

(1)总分类.U/D={{1},{6,12,18,14},{2,3,5,7,8,10,11,15,20,21}, {4,9,16,17,19,23,28},{13,22,24,26,27,31}}

共5大类即优﹑良﹑中﹑及格和不及格.

按C即C={u,v,a,r,t}分类如下：

U/C={{1,18},{2，9，13},{3，4，21},{5，7，10，20},{6，11，19},{8},{12},{14},{15},{27，16},{17，25，29},{22},{23},{24},{26},{28}，{30},{31}}

POSc(D)={{5，7，10，20},{8},{12},{14},{15},{22},{23},{24},{26}，{28},{30},{31}}

γc(D)=12/31

(2)按C-{u}即{v,a,r,t}分类如下：U/C-{u}={{1,18},{2,5,7,20,22,9,10,13},{3,4,6,11,19,21},{8},{12}，{14},{15},{16,17,25,27, 2，9},{23},{24},{26},{28},{30},{31}}

POSc-{u}(D)={{8},{12},{14},{15},{23},{24},{26},{28},{30},{31}}

γc-{u}(D)=10/31,属性u∈C关于D的重要性为：σCD(u)=γc(D)-γc-{u}(D) =12/31-10/31=2/31

(3)按C-{v}即{u,a,r,t}分类如下：U/C-{v}={{1,18},{2,9,13},{3,4,21},{5,7,10,12,20}, {6,11,19},{8},{14},{15},{16,27},{17,25,28，29},{22},{23},{24},{26},{30},{31}

POSc-{v}(D)={{8},{14},{15}{22},{23},{24},{26},{30},{31}}

γc-{v}(D)=9/31,属性v∈C关于D的重要性为：

σCD(v)=γc(D)-γc-{v}(D)=12/31-9/31=3/31

(4)按C-{a}即{u,v,r,t}分类如下：

U/C-{a}={{1,14,18},{2,9,13,17,25,29},{3,4,21},{5,7,10,20},{6,11,19},{8},{12},{15},{16,22,27},{23},{24},{26},{28},{30},{31}}

POSc-{a}(D)={{5,7,10,20},{8},{12},{15},{23},{24},{26},{28},{30},{31}}

γc-{a}(D)=10/31,属性a∈C关于D的重要性为：

σCD(u)=γc(D)-γc-{a}(D)=12/31-10/31=2/31

(5)按C-{r}即{u,v,a,t}分类如下：

U/C-{r}={{1,18},{2,3,4,9,13,21},{5,6,7,10,11,19},{8},{12},{14,15},{16,24,26,27},{17,25,29},{20},{22},{23},{28,30},{31}}

POSc-{r}(D)={{8},{12},{20},{22},{23}{31}}

γc-{r}(D)=6/31,属性r∈C关于D的重要性为：

σCD(u)=γc(D)-γc-{r}(D)=12/31-6/31=6/31

(6)按C-{t}即{u,v,a,r}分类如下：

U/C-{t}={{1,2,3},{4},{5},{6,7,8},{9},{10},{11},{12},{13},{14,15,16},{17},{18},{19},{20,21,22,23},{24},{25},{26},{27,28,29},{30,31,32},{33,34,35}}

POSc-{t}(D)={{5,7,10,20},{14},{15},{22},{23},{24},{26},{28},{30},{31}}

γc-{t}(D)=10/31,属性t∈C关于D的重要性为：

σCD(u)=γc(D)-γc-{t}(D)=12/31-10/31=2/31

由此可见，相对而言“词汇”这一部分最大程度地改变了考试等级的分类.从整体来看，该高中在今后的英语教学中应该对学生提高学习词汇的要求.

3 结束语

利用粗糙集理论中的属性重要性分析方法，对学生英语考试成绩中的各个部分进行了分析.分析表明，“词汇”部分的得分高低，对该校学生整体高考成绩的影响最大.由于粗糙集理论是在没有任何先验假设的情况下对数据进行分析，因此所得出的结论更符合实际情况.当然，我们给出的只是一个学校的例子，其结论一般情况下也只适合于该校学生，如果将此法用于对其它学校进行考生相关成绩的分析，则可能得出其它部分对整体成绩影响最重要的因素.利用粗糙集的算法，借助于计算机，可以对于更大量的数据(有时称为海量数据)进行分析，从而可以进行更为全面和客观的预测与决策.在高考信息系统中，拥有许多重要的数据，利用粗糙集理论对这些数据进行处理和分析，分析的结果将会对高中教学提供大量有用的信息，从而促进教学质量的提高.

参考文献

[1] Ming Syan Chen, Jiawei Han, Philip S Yu. Data mining:an overview from a database perspective[J].IEEET Transactions on Knowledge and Data Engineering,1996,8(6):866-883.

[2] 王国胤. Rough集理论与知识获取[M].西安:西安交通大学出版社，2001:115-131.

[3] 石 红, 沈 毅,刘志言，等.关于粗糙集理论及应用问题的研究[J].计算机工程，2003,29(3)：14-19.

[4] 曾黄麟.粗集理论及其应用(修订版)[M]. 重庆：重庆大学出版社，1998：120-125，176-189.

[5] Miao Duoqian, Wang Jue.An information-based algorithm for reduction of knowledge[J]. IEEE ICIPS′97,1997：1 155-1 158.

[6] [美]Han J.数据挖掘:概念和技术[M]. 北京:高等教育出版社, 2001:319-322.

[7] 李 勇,徐振宁,张维明. Internet 个性化信息服务研究综述[J]. 计算机工程与应用,2002,38(19):187-189.

[8] 符江东,柏文阳,蒋 明. 基于关键字的Web页面摘要生成技术[J]. 计算机应用研究,2003,20(2) :137-139.

[9] 徐 洁. 基于Java平台MVC模式的流程企业分析检测数据管理系统[J]. 计算机工程与应用, 2005, 41(15) : 215-217, 220.

[10] 于晓慧. J2EE架构下数据库访问的性能优化研究[J]. 计算机应用研究, 2005, 22(4): 90-92.