无穷时滞抽象泛函微分方程的概周期解

杜燕飞， 肖 鹏

(陕西科技大学理学院， 陕西 西安 710021)

0 引 言

关于微分方程的周期、概周期、渐进概周期、伪概周期解的存在唯一性研究[1-3]是目前微分方程定性理论中最吸引人的课题之一，其在数学以及物理学、生物数学、控制理论等领域有着重要应用. 时滞微分方程[4-6]一直受到广泛关注，其研究有着重要的理论意义，并且在控制理论和人口问题等领域有诸多实际应用价值. 本文研究了以下具有无穷时滞的抽象泛函微分方程Cauchy问题的概周期解的存在性及唯一性：

x′(t)=Ax(t)+f(t,x(t),xt)t∈[σ，σ+α]

(1)

xσ=φ∈B

(2)

其中函数f:[σ，σ+α]×X×B→X，X是Banach空间，B是(-∞,0]→X的函数组成的空间；xt属于相空间[7]B，定义为:xt(θ)=x(t+θ)，θ∈(-∞,0].

本文中，约定如下记号：C(R,X)表示所有R→X的有界连续函数f赋上确界范数的空间，即‖f‖=supt∈R|f(t)|；A∶D(A)⊂X→X在X上生成线性算子半群(T(t))t≥0，且存在常数M，c>0,使得，∀t≥0,‖T(t)‖≤Me-ct.

1 基本定义及引理

定义1 称连续函数f∶R→X为概周期函数，若∀ε>0，存在lε>0，使得每一个长为lε的区间上都存在一个τ使得

‖f(t+τ)-f(t)‖<ε

成立,记为f∈AP(X),称τ为f的ε-平移向量.

定义2 函数f∶R×X×P→X，如果∀ε>0，紧集K1⊂X和K2⊂P，∃lε>0，对于任意R中长度为lε的区间上都存在一个τ,使得

‖f(t+τ,x,φ)-f(t,x,φ)‖<ε(t∈R,x∈X,φ∈P)

成立，则称f(t,x,φ)关于t∈R是一致概周期的，即f(t,x,φ)是t的概周期函数，且对(x,φ)∈X×P是一致的, 记为f∈AP(R×X×P,X).

引理1[7]若u(t)∈AP(X)，则函数t→ut∈AP(B).

引理2[1]AP(X)是Banach空间.

定义3 相空间[7]B表示(-∞,0]→X的函数向量空间，赋半范‖·‖B，使得下列命题成立：

(H1) 若x:(-∞,σ+α)→X，(α>0),在[σ，σ+α]上连续，且xσ∈B，则∀t∈[σ，σ+α]，下列条件成立：

(1)xt∈B； (2)‖x(t)‖≤H‖xt‖B(H为常数)； (3) ‖xt‖B≤K(t-σ)sup{‖x(s):σ≤s≤t‖}+M(t-σ)‖xσ‖B.

(H2)空间B是完备的.

引理3[7]对于任意连续函数φ:(-∞,0]→X，存在常数k>0，使得‖φ‖B≤k·supθ≤0‖φ(θ)‖.

2 主要结果

引理4 若f(t,x,φ)∈AP(R×X×B,X)，x(t)∈AP(X),φ∈AP(B). 设f(t,x,φ)满足

‖f(t,x,φ)-f(t,y,ψ)‖≤Lf(‖x-y‖+‖φ-ψ‖B)

∀t∈R,x,y∈X,φ,ψ∈B成立，其中Lf>0为常数，则复合函数g(t)=f(t,x(t),φ(t))∈AP(X).

证明：

‖g(t+τ)-g(t)‖=‖f(t+τ,x(t+τ),φ(t+τ))-f(t,x(t),φ(t))‖

≤‖f(t+τ,x(t+τ),φ(t+τ))-f(t,x(t+τ),φ(t+τ))‖+‖f(t,x(t+τ),φ(t+τ))

-f(t,x(t),φ(t))‖≤ε+Lf‖x(t+τ)-x(t)‖+‖φ(t+τ)-φ(t)‖B)

由x(t)∈AP(X)，φ∈AP(B)，上式≤(1+2Lf)ε,所以，f(t,x(t),φ(t))∈AP(X).

定理1 若g(t)∈AP(X)，则抽象泛函微分方程的Cauchy问题

x′(t)=Ax(t)+g(t)t∈[σ，σ+α]

(3)

xσ=φ∈B

(4)

有唯一的概周期mild解.

由于g(t)∈AP(X)，令τ为g(t)的ε-平移向量，则

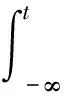
定理2 若f(t,x,φ)∈AP(R×X×B,X)，且

‖f(t,x,φ)-f(t,y,ψ)‖≤Lf(‖x-y‖+‖φ-ψ‖B)

∀t∈R,x,y∈X,φ,ψ∈B成立，其中(1+k)MLf/c<1，则时滞抽象泛函微分方程的Cauchy问题

x′(t)=Ax(t)+f(t,x(t),xt)t∈[σ，σ+α]
xσ=φ∈B

有唯一的概周期解.

f(s,v(s),vs)ds∈AP(X),因此G是把AP(X)映射到自身的变换.下面证明G是压缩映射.

≤[(1+k)MLf/c]‖v1-v2‖≤‖v1-v2‖

参考文献

[1] Chuanyi Zhang. Almost Periodic Type Function and Ergodicity[M]. Science Press (Kluwer Academic Publishers), 2002:87-194.

[2] C. Zhang. Pseudo almost periodic solutions of some differential equations 2[J]. J. Math. Anal. Appl., 1995, 192(2):543-561.

[3] 杜燕飞, 肖 鹏. 热传导方程Cauchy问题的概周期解[J]. 安徽大学学报, 2008, 32(6):14-17.

[4] Y. Hino, S. Murakami. Almost automorphic solutions of abstract functional differential equations[J]. J. Math. Anal. Appl., 2003, 286:741-752.

[5] 王良龙, 王志成. 一类无穷时滞泛函微分方程解的渐近性态[J]. 安徽大学学报, 2001, 25(4):1-6.

[6] G. M. N′Guérékata. Existence and uniqueness of almost automorphic mild solutions to some semilinear abstract differential equations[J]. Semigroup Forum, 2004, 69(1):80-86.

[7] Hino, S.Murakami, T.Naito. Functional-Differential Equations with Infinite Delay[M]. Lecture Notesin Mathematics, 1991:50-110.