电磁继电器振动极限加速度分析方法

任万滨 陈英华 康云志 王立忠 崔 黎

（1.哈尔滨工业大学军用电器研究所 哈尔滨 150001 2.桂林航天电子有限公司 桂林 541002）

1 引言

电磁继电器是一种自动运动电器。由于具有转换深度高、多路同步切换、输入输出比大、抗干扰能力强的特点，因此广泛应用于信号传递和执行控制系统中。在机械振动与冲击的工作环境下，接触压力的周期性变化将使继电器的电参数（接触电阻、吸合电压、释放电压）和时间参数发生明显变化。机械过载情况下将引起闭合触点抖断或断开触点抖闭的失效模式，严重时甚至会造成触点微动磨损及机械构件疲劳断裂现象的发生。

通常将保持继电器触点可靠接触的最大振动加速度定义为振动极限加速度，并将继电器固有频率与振动极限加速度作为衡量其耐力学环境能力的两个重要指标。大多数继电器中的常闭触点—簧片组是整机中最易谐振的部分，因此以往的研究也多集中于此。早期Chambega 将电磁继电器中的接触系统等效为单自由度系统，通过对固有频率和振动加速度的求解，得到了振动环境下继电器动作时间减小与释放电流增加的结论[1]；Ройзе 以典型平衡衔铁式继电器为例，将其中动簧片视为固定—铰支梁结构的连续系统，应用振动力学理论分析了触点处的振动特性[2]，所得的固有频率和振动极限加速度计算公式一直是目前继电器抗振性设计的理论依据。考虑到触头—簧片的结构特征，文献[3]提出了确定触簧系统振动加速度的方法，并通过引入接触刚度建立了相对完整的柔性接触系统结构动力学方 程[4]。 进而应用大型有限元仿真分析软件MSC.Patran/Nastran 确定了通用型电磁继电器整机的结构动力学特性，对其结构薄弱环节的准确定位及优化具有指导作用[5]。

本文通过对典型电磁继电器结构运动特征分析，应用有限元法思想推导出包含拉簧、衔铁和触簧组零件构成的运动组件质量矩阵和刚度矩阵，并根据相容性条件建立了衔铁触簧组在模态坐标下的结构动力学方程。通过数值计算得出继电器结构的固有频率和常闭触点间的接触力响应，从而确定了继电器激振频率与振动极限加速度的关系。另外通过所研制的实验测试系统完成了振动状态下继电器触点接触电阻的变化规律与触点运动过程的拍摄，不仅验证了本文提出的振动加速度分析方法的正确性，而且对继电器在振动环境中接触失效机理的确定具有重要意义。

2 电磁继电器结构动力学数值模型

典型通用电磁继电器结构如图1 所示。其电磁系统由L 状轭铁、线圈和平直状衔铁组成。衔铁与动簧片通过绝缘模塑件铆装在一起构成运动组件，动作时将以轭铁刀口作为支点完成吸合与释放，同时带动动触头完成其与静触头之间的转换。衔铁端部的拉簧在整个过程中提供机械反力。

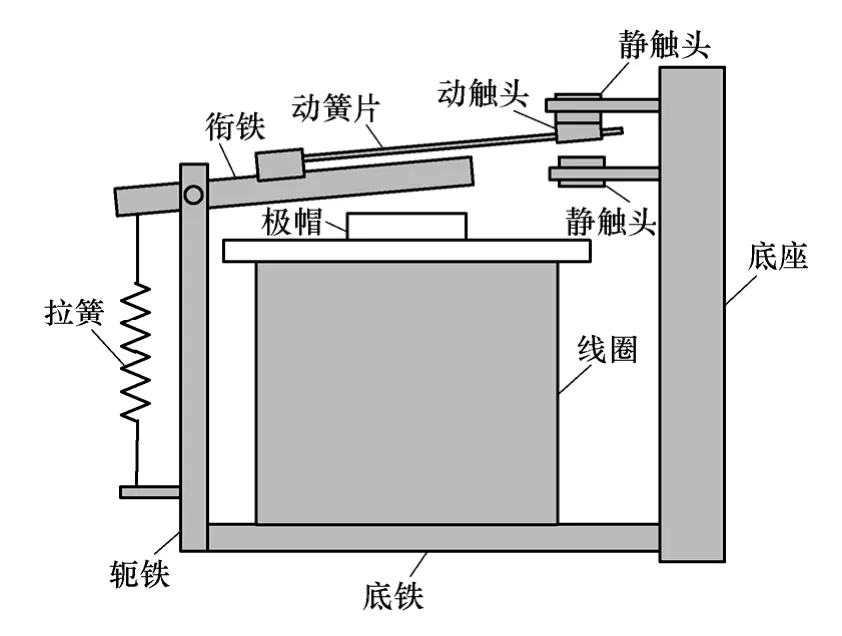
图1 电磁继电器结构示意图 Fig.1 The typical schematic structure of relay

衔铁触簧组具有刚体与柔体耦合运动的特征，这类动力学模型称为柔性多体系统或刚—柔混合多体系统。考虑到振动方向为与触头运动方向一致时对继电器影响最敏感，本文将对此重点分析。

结合有限元法思想分别将图1 中衔铁与动簧片沿长度方向上的关键位置划分为平面梁单元，单元及节点编号如图2 所示。其中1～3 段为衔铁单元，4～7 段为动簧片单元，kf为拉簧刚度，kj为接触刚度，定义及取值可参阅文献[4]。节点③为衔铁支承点，因此只保留其平面转动自由度，节点④是衔铁与动簧片的铆接点，节点⑨包含动触头的集中质量m0，节点①、③、⑩为振动加速度载荷位置。同时考虑轴力、弯矩和剪力作用下的梁单元刚度对称阵为

式中 A—单元截面积；

l—单元长度；

I—单元惯性矩。

图2 单元划分及节点定义 Fig.2 The divided elements and nodes definition

质量对称阵为

触头质量等效对角阵为

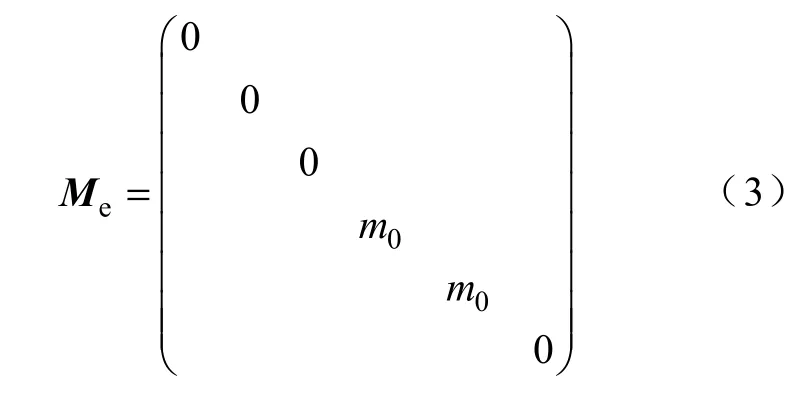
拉簧与接触弹簧刚度等效矩阵为

单元的阻尼矩阵采用Rayleigh 阻尼，表达式为

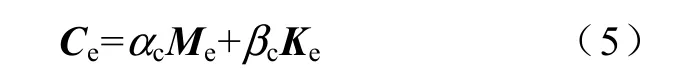
最后通过叠加原理将模型中的单元叠加成 30×30 的刚度矩阵K，质量矩阵Μ 和阻尼矩阵C，则系统运动方程为

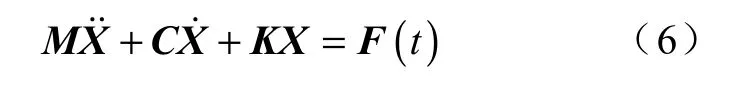
将阻尼矩阵C 设为零，并将节点①、③、⑩固定，选取子空间迭代法求解式（6）所得的特征值和特征矢量，即为系统的固有频率ωi与主振型Φi。

利用系统自由振动的主振型可将矩阵K，Μ，C和激振力F 对角化，即

从而系统解耦成互不相关的子系统，各子系统的频率响应为

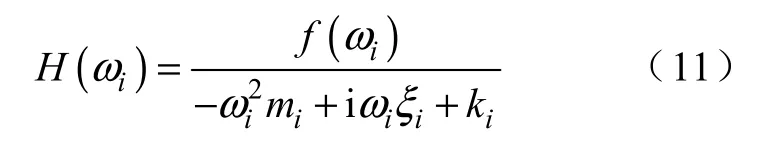
各子系统在激励条件下的响应进行叠加经变换

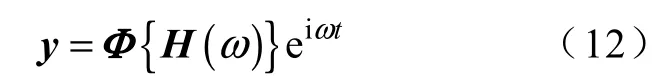
即得整个系统的强迫振动响应，则触头接触力响应为

式中，y9、y10分别为动触头与静触头的y 向位移响应。

3 计算实例与实验验证

3.1 计算实例

某继电器的主要尺寸参数见下表。由此计算得到衔铁触簧组的固有频率值与模态振型，图3 所示为一阶模态主振型，即衔铁转动带动动簧片弯曲振动模式，固有频率为328Hz。更高阶的固有频率与模态特征均远远超出本文的研究范围，因此不作讨论。为便于实验验证，首先基于低阶模态及相应的特征值得到节点④与静触头间相对位移响应。图4为振动频率范围为10～800Hz，振动加速度为49m/s2的相对位移幅值，在共振频率处相对位移出现峰值109.54μm。

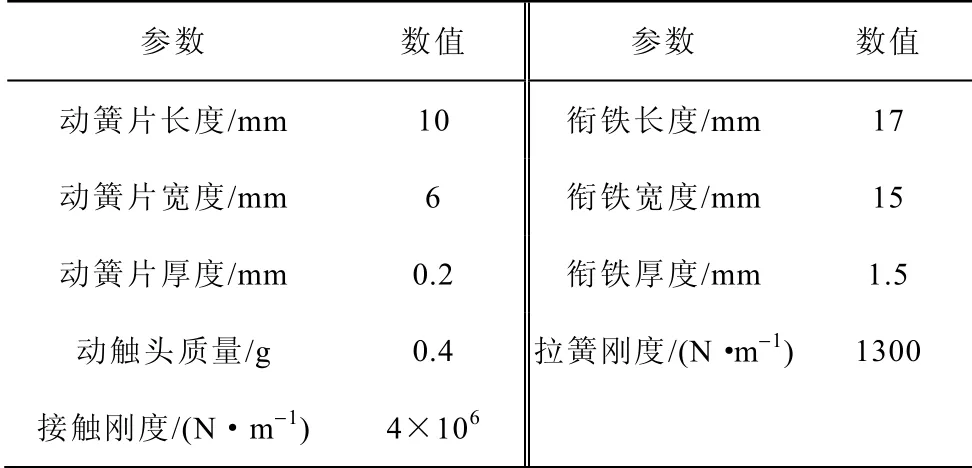
表 主要尺寸参数 Tab. Main size parameters of relay

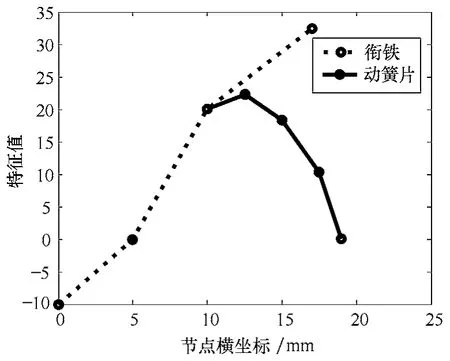
图3 系统一阶主振型 Fig.3 The first order main vibration shape

图4 触点位移响应 Fig.4 Comparisons between experiment and simulation

3.2 实验验证

为验证理论分析的正确性以及数值计算结果的精确性，本文建立了如图5 所示的电磁继电器振动实验系统。由DSP 处理器驱动功率放大模块实现对电磁振动台正弦振动的控制，系统中加入加速度传感器、电荷放大和数据采集模块，可实现对振动台的闭环控制。实验过程中应用高粘度胶将继电器底铁粘在电磁振动台台面上，振动实验中的激励条件如图6 所示。应用Phantom V7.3 型高速摄像机（拍摄速度设定为10 000 帧/s）。接近共振区域，即250～450Hz 内，激振频率以5Hz 步长递增，其他非共振 区域内以50Hz 步长递增，依次拍摄衔铁触簧组的动态过程。选取图7 中的2 点（静触头）作为位移参考点，动簧片的左端根部1 点（位移最大，接近节点④）为观察点，通过计算图片中1 点和2 点的像素间最大距离确定各激振频率下其间的相对位移响应，得到激振频率与两点间相对位移响应关系如图4 所示。由此可见，实验测试结果与数值计算结果十分接近，且当激振频率为340Hz 时相对位移曲线存在峰值99μm，该状态可判定为衔铁触簧组的共振情况。

图5 继电器振动实验系统 Fig.5 The schematic diagram of test system

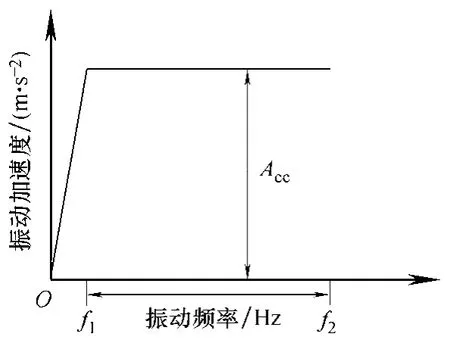
图6 扫频振动加速度波形 Fig.6 The sweep frequency vibration waveform

图7 触簧系统实物照片 Fig.7 Photo of one spring-contact group

4 继电器振动极限加速度的确定与分析

通过动力学方程的求解可获得触簧系统固有频率及动触头与静触头间的接触压力响应，并最终以触头间接触压力变化量ΔFc不大于初始压力F0作为触点保持接触状态的极值条件。

在已知触头间初始压力为0.38N 情况下，应用前述数值计算方法得到了继电器在不同激振加速度条件下的扫频振动特性，从而确定了邻近共振区域内不同激振频率条件下导致继电器触头分断失效的最小振动加速度，即继电器的振动极限加速度值。如图8 所示，在共振频率下，振动极限加速度具有最小值42m/s2，即抗振性最差，随着激振频率远离共振点，继电器所能承受的振动极限加速度逐步升高，触头抖断对应的激振频带逐步加宽。因此衡量继电器的耐振动能力应首先判断其是否工作在共振频率条件下，对于工作在谐振条件的以共振频率对应的振动极限加速度作为其耐力学环境能力的判据，对于工作在非谐振条件的以其最大激振频率对应的振动极限加速度衡量。

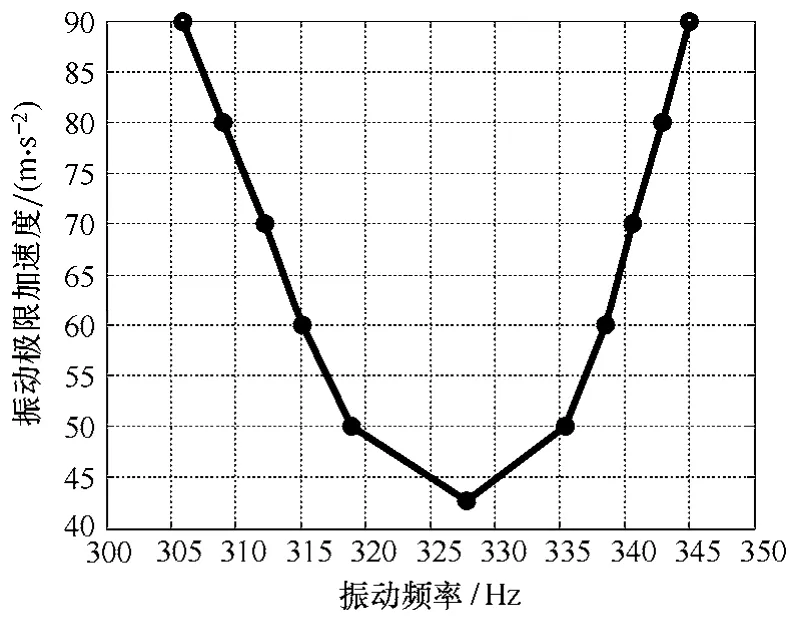
图8 继电器振动极限加速度与固有频率关系 Fig.8 The relationship between limit vibration acceleration and excited frequency range

另外，可通过式（13）所得的接触压力变化量代入式（14）中确定接触电阻的变化。由此计算所得的扫频振动条件下接触电阻特性如图9 所示。

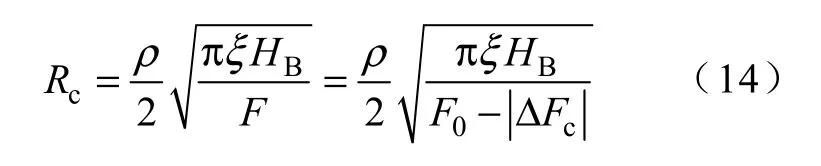
式中 ρ —电阻率；

HB—硬度；

ξ =0.3。

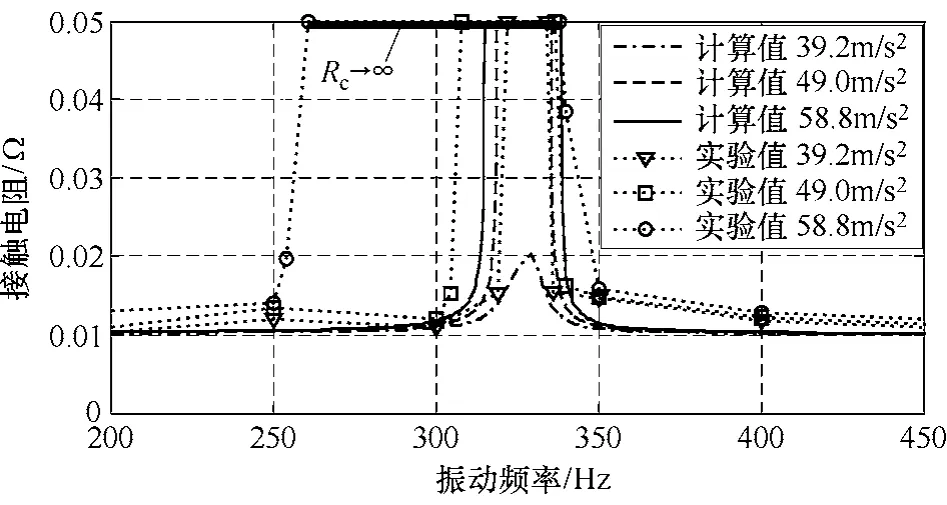
图9 扫频振动条件下的接触电阻特性 Fig.9 The relationship between contact resistance and excited frequency and vibration acceleration

同时应用四线法可监测振动状态下继电器触头的导通电流和接触电压，从而实验确定接触电阻的瞬时值。由图9 可见，接触电阻在趋近共振区域内存在急剧增大，且呈现触点断开（Rc→∞）现象，随着振动加速度的不断增大，触点抖断对应的激振频带亦变宽。考虑到实验测试过程中影响继电器接 触电阻参数的因素很多，因此测试值较计算值偏大。

5 结论

电磁继电器的衔铁触簧组具有刚柔耦合的结构特征，是振动环境中导致接触失效的主要组件。本文对此提出了一种用于分析其固有频率及接触力强迫振动响应的数值分析方法，从而得到了使继电器触点接触可靠的振动极限加速度与激振频率间的关系。在振动实验过程中通过测试触头位移响应与接触电阻，确定了继电器的振动失效模式，对电磁继电器耐力学环境性能的提高具有参考价值。

[1] Chambega D J.Qualitative analysis on the effect of external vibrations on the performance of relays[C].Proceedings 1996 4th IEEE AFRICON Conf.Part2,1996:1035-1039.

[2] B.3.罗依金.小型密封电磁继电器[M].王蓉芳,译.北京:人民邮电出版社,1979.

[3] 翟国富,任万滨,许峰,等.电磁继电器触簧系统振动极限加速度的分析方法[J].振动工程学报,2004,17(1):66-71.

Zhai Guofu,Ren Wanbin,Xu Feng,et al.Analysis method for vibration acceleration of electromagnetic relay[J].Journal of Vibration Engineering,2004,17(1):66-71.

[4] Ren Wanbin,Zhai Guofu,Cui Li.Contact vibration characteristic of electromagnetic relay[J].IEICE Transactions on Electronics,2006,E89-C(8):1177- 1181.

[5] Ren Wanbin,Chen Yinghua,Zhai Guofu.Modeling and simulation of hermetically sealed electromagnetic relay under mechanical environment[J].IEICE Transactions on Electronics,2007,E90-C(7):1448- 1454.

[6] Paul G Slade.Electrical contacts principles and applications[M].New York:Marcel Dekker,1999.