二冲程汽油机簧片阀流固耦合仿真分析
刁 璇,杨海青
(南京航空航天大学能源与动力学院,南京 210016)
对二冲程发动机而言,进气方式可分为对称进气和非对称进气两种。对称进气方式虽然结构简单、可靠,但存在高速和低速性能矛盾的缺点。由簧片阀控制的非对称进气方式在中低速不会产生反喷,稳定性和经济性较好[1]。
本文的研究对象是二冲程发动机进气系统中关键节流部件簧片阀。国内外很多关于簧片阀的研究主要侧重于以实验方式测量在发动机工作过程中簧片阀升程随曲轴转角的变化关系,以及采用数学理论推导的方式分析阀体内的气体运动以及簧片的振动特性[2-5]。前者必须在簧片阀结构生产加工出来后才能进行,若以此种方式进行簧片阀的预研工作,则成本高且效率低;后者可作为研究簧片阀内部流体与簧片运动机理的手段,但难以直接运用于工程实践中。
采用数值模拟的方法可以有效地预测簧片的运动,极大地缩短设计开发周期,并能获得一些采用实验研究法所无法得到的参数,如簧片阀体内的流场与压力分布等[6-7]。在很多场合下,数值模拟的研究方法具有无法取代的优势。因此,研究适合簧片阀的仿真方法很有必要。
对于二冲程发动机中簧片阀的仿真工作,国内外相关的研究并不是很多。国内有采用一维仿真方法计算簧片阀的升程和流量的研究;国外有学者进行过一维数值模拟、二维计算流体力学(CFD)的研究,并在此二维模型的基础上进行了流固耦合(FSI)研究[8],以及采用Fluent软件中用户自定义功能(UDF)控制簧片运动的轨迹进行三维 CFD 计算研究[9]。
本文采用基于Ansys Workbench的双向流固耦合仿真研究方法。它不同于借助第三方软件(如MPCCi)进行流体域与固体域数据交换,所有流体域与固体域的计算及数据交换都在Workbench平台中完成。该方法也不同于前文中提到的采用Fluent软件中的UDF控制簧片运动轨迹实现流体与固体的“同时计算”。每个瞬间作用在簧片上每个位置的流体力都由软件计算流体运动得到,而簧片的变形对流体域的影响将通过Fluent软件中动网格功能实现,在每个时间步长点上进行流体域与固体域的耦合计算。只要时间步长取得足够小就能无限接近每个瞬时的耦合计算,即能无限接近实际的簧片阀内运动。
1 簧片阀运动原理
1.1 簧片阀基本结构
簧片阀安装在二冲程发动机进气系统中,位于曲轴箱前面,控制发动机的整个进气过程。在阀类型上属于单向阀,可防止在发动机进气过程中流过阀体的气体出现反喷现象,有效确保了进入曲轴箱中的进气量。阀体主要由阀壳、阀芯、簧片、限位板组成。簧片有6块,每3片一组,分别位于上下两侧,通过螺钉将簧片与限位板紧固在阀芯上。簧片阀模型见图1,物理参数见表1。

图1 簧片阀模型
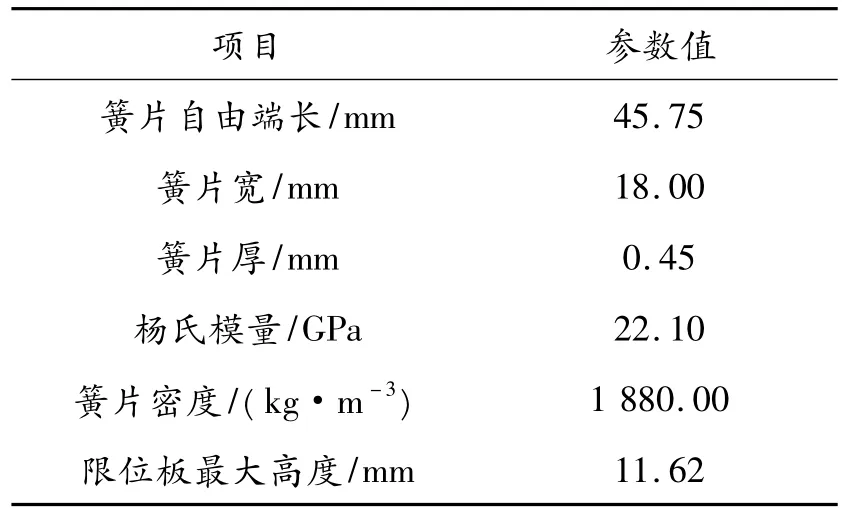
表1 簧片阀物理参数
1.2 簧片阀流体域(气体)数学模型
簧片阀位于进气管与曲轴箱之间,在发动机进气过程中,流过簧片阀气体的运动过程十分复杂。这是由于在进气过程中进气管中的气体压力是不断波动的,且曲轴箱受活塞上下运动的影响不断向缸内扫气的过程导致了曲轴箱中气体压力也在不断地变化。在进气过程中,气体存在热交换的过程,使得气体的温度也会发生变化。因此,需要对实际流动过程做必要的简化及假定[10-11],具体如下:
1)只考虑空气在簧片阀内的流动,忽略进气道喷射型(PFI)发动机进气系统中的燃油成分。
2)气体在簧片阀内的流动没有热交换,认为是绝热流动过程,比热容保持不变。
3)认为进气压力是不变的,不考虑进气管中的压力波动;考虑到阀内的气体在流通方向的流量及速度远大于另两个方向,将流动过程当做一元定常等熵过程处理。
4)将在簧片阀内流动的气体视为理想气体,即气体严格遵从理想气体状态方程。
图2为簧片阀内气体流动的情况。进口处气体的压力、温度、密度分别为 P0,T0,ρ0;气体的流速为V0;簧片阀出口处的气体压力、温度、密度分比为 P1,T1和 ρ1;气体流速为 V1。

图2 簧片阀内流动情况
根据理想气体的一元定常流动能量方程[12-13]:
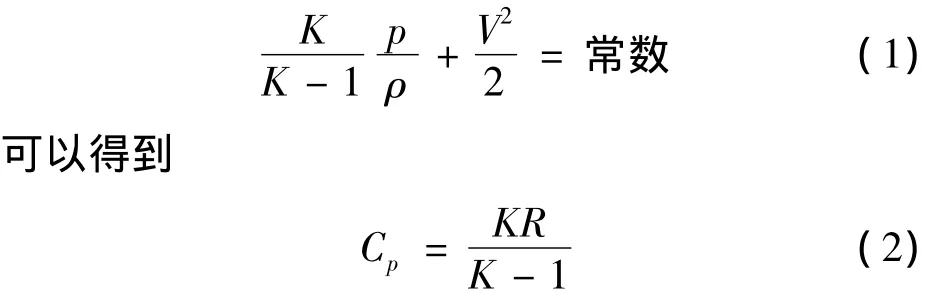
气体流过簧片阀的一元等熵流动伯努利方程为
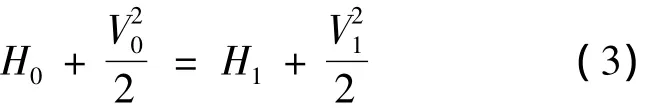
对于理想气体则有

式(1)~(4)中各物理量分别为:P为压强(Pa);ρ为密度(kg/m3);H为焓(J/kg);K为等熵指数;Cp为定压比热容(J/kg·k)。
由式(3)与(4)得到
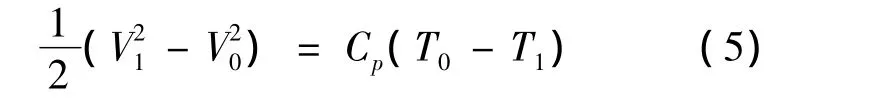
将式(2)代入式(5)得到

由气体连续性方程得到通过簧片阀的气体质量流量微分方程为
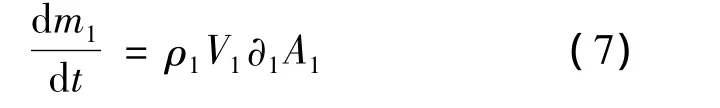
式(7)中:m1为通过簧片阀的气体质量(kg);∂1为簧片阀流量系数;A1为簧片阀出口截面积(m3)。
将式(6)代入(7)中得到通过簧片阀气体质量流量微分方程:
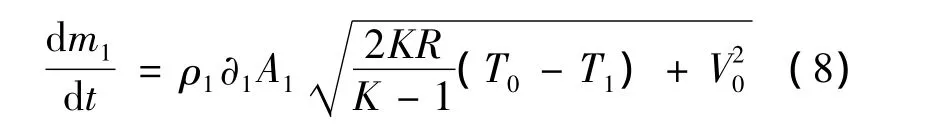
1.3 簧片阀固体域(簧片)振动特性
在簧片运动过程中,当外力的频率达到簧片的固有频率时,簧片的振幅会达到最大,此时簧片的应力与应变会非常大,对限位板和阀芯的撞击也最为剧烈,十分容易损伤簧片。因此,应保证在发动机工作过程中,气体推力的频率应远离簧片的固有频率。对本文研究的簧片阀所安装的发动机来说,设计工况点为6300 r/min,二冲程发动机曲轴每转一圈,发动机完成一次工作循环,则簧片阀需要开启一次。在发动机处于设计工况点时,气体推力的频率为105 Hz,应保证在设计工况点气体的推力频率小于簧片的固有频率。
根据簧片的结构和安装情况,可将簧片视为等截面的悬臂梁来研究其振动特性。需要说明的是,本研究不考虑簧片的振动阻尼,只研究簧片在主弯曲平面里的弯曲振动,不考虑剪切力的影响[11]。图3为悬臂梁形状的簧片模型。

图3 悬臂梁结构簧片模型
本研究中:Q为截面切力;Z为弯曲位移;M为截面弯矩;ρ为簧片密度;EI为弯曲刚度;A为截面积。由于这里研究簧片的固有特性,故令作用在簧片上的气体推力为0。
对照模型图3,根据达朗贝尔原理建立Z方向上的力平衡方程:
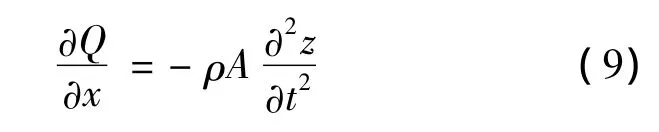
再建立任意微元段力矩平衡方程:

忽略dx的二阶小项得到

整理式(9)与(11)得到簧片自由振动方程:
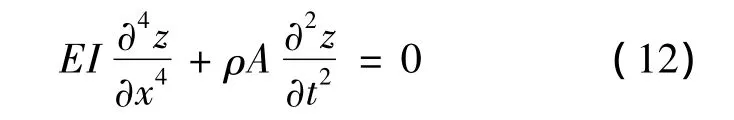
代入悬臂梁结构所对应的边界条件:x=0,Z(0)=Z'(0)=0;x=l,Z″(l)=Z‴(l)=0。
求解式(12)可以得到簧片振动的频率方程:
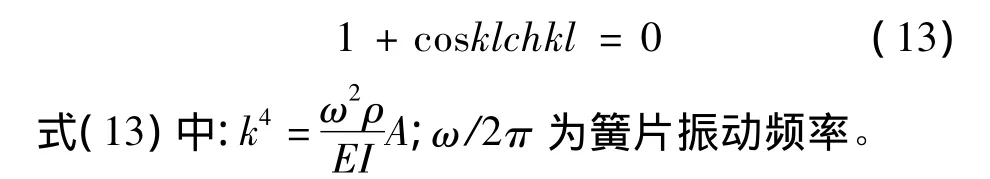
利用Matlab软件求解方程(13),发现该方程有无穷多的解,对应了簧片振动的多个固有频率。取第1阶固有频率与发动机气体推力频率对比,更高阶的固有频率远大于发动机中气体的推力频率,不需要考虑。计算得出k1l=1.8751。再由k与ω的关系以及表(1)中簧片的尺寸、物理参数求出第1阶固有频率ω1/2π约为120 Hz。发动机在设计工况点的气体推力频率为105 Hz,小于簧片的1阶固有频率,在该转速附近不会发生共振,保证了簧片阀在最常用工况下的使用安全。但当发动机转速接近7200 r/min时,气体推力的频率就会接近簧片的1阶固有频率,应避免发动机长时间工作在该转速附近。
2 簧片阀双向流固耦合仿真模型
2.1 簧片阀双向流固耦合仿真原理
图4为簧片阀双向流固耦合计算原理。
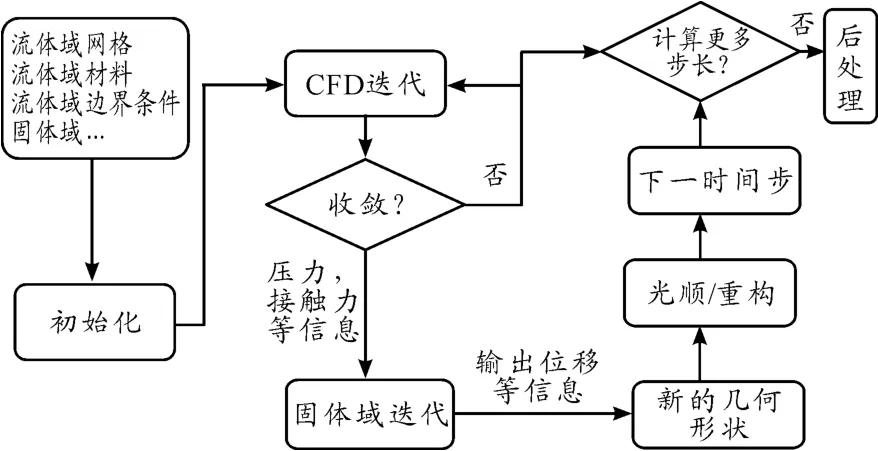
图4 簧片阀双向流固耦合计算原理
如图4所示,进行簧片阀双向流固耦合计算时,首先要分别对流体域以及固体域进行网格划分、设置边界条件、选定材料属性;然后初始化模型;先在流体域进行CFD计算,当计算收敛后,流体软件将计算得到的流体信息传递给固体计算软件,固体计算软件根据流体信息计算出固体域的变形信息;变形后的固体会产生新的流场几何边界,流体软件通过动网格的光顺和重构功能得到新的流体域网格,并进行下一时间步的流体CFD计算;当设定的所有时间步计算完成后,就可以导出流体域和固体域的计算结果进行后处理。
2.2 仿真模型的建立
在Ansys Workbench14.0版本中建立簧片阀流固耦合仿真模型,如图5所示。几何建模采用UG软件,然后倒入Workbench的几何模块中。流体部分采用Fluent软件计算,固体部分采用Transient Structure模块计算,流体域与固体域的数据交换采用System Coupling模块完成。
2.2.1 流体域模型建立
建立模型时使用Workbench中自带的Meshing画网格工具。由于存在动网格区域,所以网格类型选择四面体,网格量为154584。湍流模型为k-ε两方程模型,近壁区采用标准壁面模型。采用基于压力、绝对速度的SIMPLE求解方式。对流差分格式为1阶迎风格式。动网格方法采用Smoothing和Remeshing,将流体域和固体域需要进行数据交换的面设置为System Coupling类型的动网格区域。流体域网格模型如图6所示。
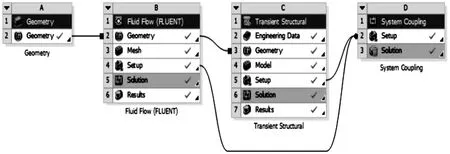
图5 Workbench中仿真模型
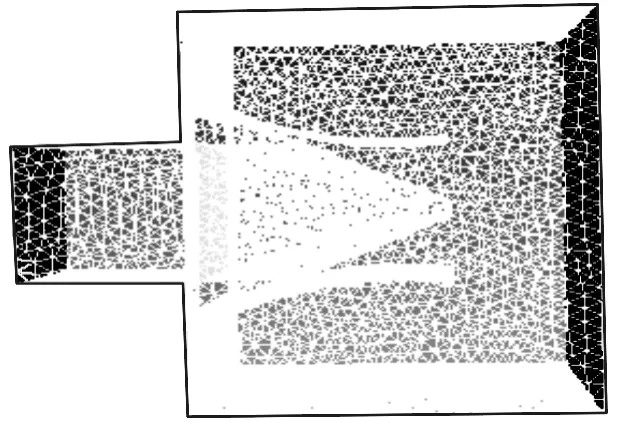
图6 流体域网格模型
2.2.2 固体域模型建立
固体域为簧片阀的6块簧片。该型簧片阀的6块簧片是相互独立的,在根部没有互相连接,不需要对簧片做分离的简化。考虑到流体域是划分的四面体网格,为保持流体域与固体域在接触面上网格类型的一致性,在Transient Structure模块中采用Meshing工具划分四面体网格,网格量为38946。对固体域需要设置约束条件,将簧片被螺钉固定在阀芯上的一端设置为Fixed Support约束类型。其他5个面均与流体接触,受到流体力的影响,设置为Fluid Solid interface。约束类型如图7所示。

图7 簧片约束类型
2.2.3 流体域与固体域数据交换模块设置
System Coupling模块负责处理流体与固体的数据交换,需要在该模块中设置耦合计算的时间信息,且要保证与流体域及固体域中设置的计算时间信息一致。将流体与固体需要进行数据交换的面设置成Data Transfer类型。还需要说明流体与固体哪一个首先进行计算。对于流体驱动固体运动的问题,应将流体设置为首先进行计算。
3 仿真结果分析
3.1 定常边界条件下仿真结果分析
保持簧片阀仿真模型的进出口压力不变,研究在固定压差下,簧片在气体压差力作用下的升程。本文研究了在5组不同的气体压差力(以大气压为单位)下簧片的尖端升程曲线和簧片阀中气体流场变化。表2列出了在5组气体压差下的簧片阀稳定升程值。图8为各组压差下簧片升程曲线图。
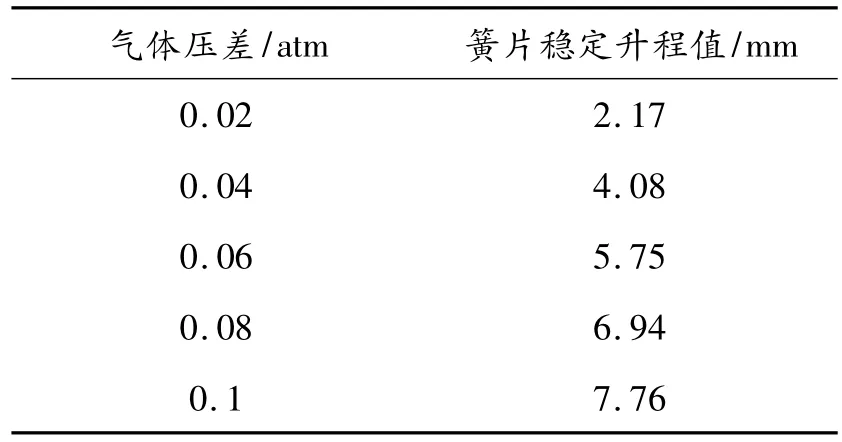
表2 不同气体压差对应的簧片升程值
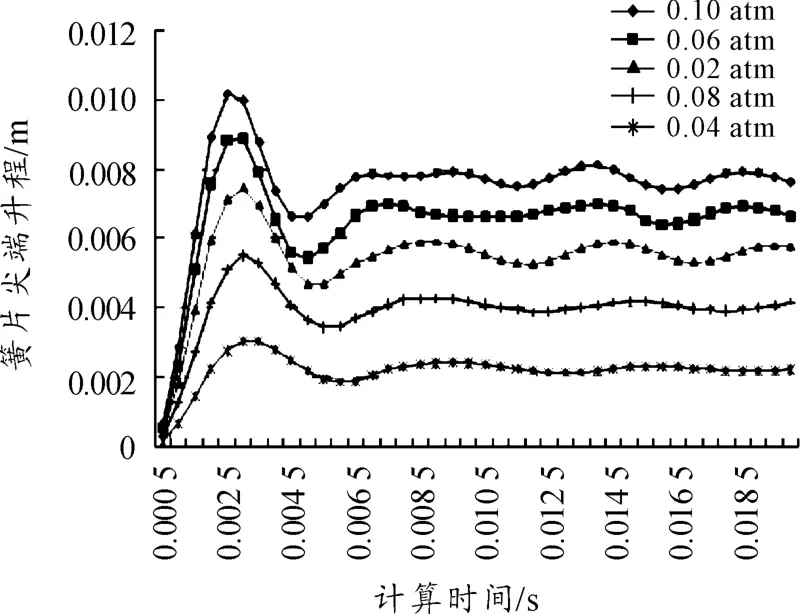
图8 不同压差下簧片升程曲线
从图8可以看出:当簧片阀前后气体压差保持不变时,簧片的升程是从0开始,最终稳定在一个较小区间内的过程。当计算时间足够长时,簧片的升程会最终稳定在区间内的某个值,此时簧片的升程就是理论上在某一压差下的稳定升程值。但考虑到计算机性能有限,计算双向流固耦合问题需要的时间很长,所以当簧片升程波动足够小时,取波动区间的中间值作为簧片升程最终的稳定值。
分析图8中升程曲线的变化规律可以发现:在簧片阀进出口气体压差力作用下,在簧片变形初期,簧片的升程会到达一个较大的波峰。此时,簧片的升程值为整个变化过程中的最大值,但簧片无法一直保持在该位置。在该波峰过后,簧片的升程值会迅速下降,下降到一定值之后,簧片的升程值会再次上升,但幅度远低于首次上升时的值。之后,簧片升程值会不断的上下波动,试图寻求一个平衡位置。
出现上述变化规律的原因可以从使簧片发生变形的作用力来考虑。作用在簧片上的力有两方面组成:一是簧片前后空气的压差力;二是簧片自身的回弹力。簧片的升程变化规律其实正反映了这两种力的变化过程。当气体压差力大于簧片的回弹力时,簧片的升程会增大;当回弹力大于气体压差力时,升程会减小。直到气体压差力与簧片的变形程度处于相对平衡时,簧片的升程才会稳定在某一位置。图9可见簧片中最小应力变化,以此来说明簧片的回弹力变化过程。

图9 不同压差下簧片尖端应力值
对比图8与图9可以发现:簧片尖端应力变化过程与簧片升程曲线的总体趋势保持一致,符合实际的变化规律。由于簧片的变形过程是非线性的,簧片的升程越大,则簧片内产生的应力也越大,产生相同的升程变化量所需的气体压差力也越大。从表2就可以看出这一点。图10为0.1 atm气体压差下簧片阀截面总压云图,设置的操作工况为1 atm,反映了气体通过压差逐步打开簧片的过程。

图10 0.1atm气体压差下簧片阀内总压云图
从图10也可以看出:在簧片的运动过程中,虽然簧片阀进出口面上压力保持不变,但簧片周围的气体压力是在不断变化的,它与簧片的回弹力一起控制着簧片的变形程度。图11为在不同压差下通过簧片阀的气体体积流量。
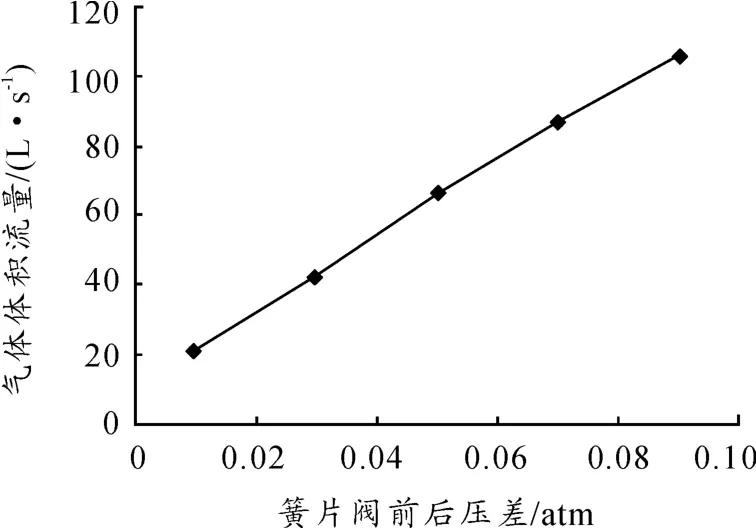
图11 不同压差下通过簧片阀气体体积流量
3.2 非定常边界条件下仿真结果分析
非定常边界条件需要控制进出口面上的压力随时间发生变化,利用Fluent软件中用户自定义功能(UDF)来实现,入口面上的压力变化规律如图12所示,出口面压力为99 Pa。
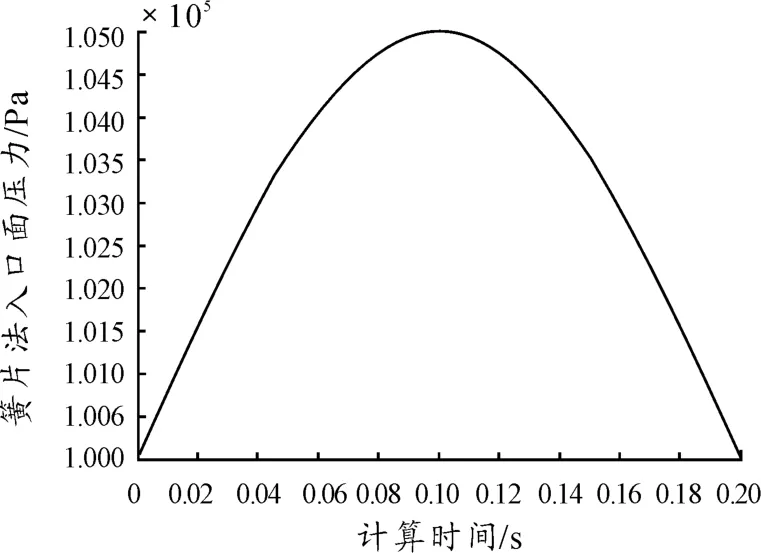
图12 入口面压力变化图
进出口面上的气体压差最小为1 Pa,最大为6 Pa,最大压差出现在0.01 s这一时刻。通过流固耦合计算来验证簧片的升程曲线能否响应边界压力的变化规律。图13为计算得到的簧片升程曲线。
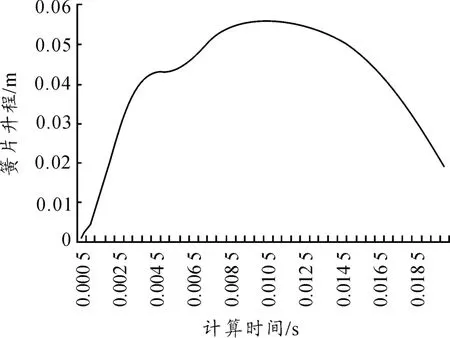
图13 非定常边界条件下簧片升程曲线
图13表明了簧片升程曲线符合边界压力的变化规律:升程曲线随入口面压力增大而增大、减小而减小,并在0.01 s时达到了最大值。因为设置了最小压差1 Pa,所以在簧片运动的初期,升程上升得较快,一段时间后升程上升速度放缓,出现了一个波峰,这类似于定常边界条件下簧片升程曲线上第一个波峰的形成原因;在计算结束时,簧片的升程比1 Pa固定压差下的稳定升程要大,原因是受到了上游较大气体压差的影响。说明簧片升程能准确地响应边界面上的压力变化,则可以完善对二冲程发动机的三维CFD数值模拟工作。此前对二冲程发动机的CFD模拟工作大都是以扫气道入口面作为整个模型的入口边界,取曲轴箱中气体的平均压力作为入口面上的压力边界条件。这种方法忽略了整个进气系统对发动机进气过程的影响,与发动机实际的工作情况存在较大差距。
4 结束语
1)分别对簧片阀内气体流动情况和簧片振动特性做了说明,得到了通过簧片阀的气体质量流量微分方程,并计算得出簧片的固有频率,分析了簧片的共振情况。
2)对簧片阀分别进行了定常边界和非定常边界条件下的流固耦合仿真计算,得到了定常边界条件下簧片的升程变化曲线、阀体内部气体压力云图和通过簧片阀的气体流量;证明了在非定常边界条件下,簧片升程能够响应边界面上压力的变化,从而可以进一步完善二冲程发动机整机三维CFD数值模拟的工作。
本文对簧片运动过程的研究没有涉及簧片撞击限位板和阀芯的过程。对于不同边界条件下,簧片撞击限位板和阀芯会产生多大的冲击应力及簧片的弹跳高度等问题,需要在今后的工作中做进一步研究。对于二冲程发动机整机的CFD模拟工作,由于模型的网格量较大,且存在模拟活塞运动的动网格区域和簧片阀流固耦合区域,对计算机配置要求较高,故最好采用高性能计算机进行计算。
[1]杨光兴,叶茂炎,程善斌.摩托车发动机原理与设计[M].武汉:武汉测绘科技大学出版社,1993.
[2]黄伟.NF50摩托车发动机簧片阀座组合的试验研究[J].摩托车技术,1998,3:7 -8.
[3]由丽娜,毛华永,戴永圣.小型二冲程汽油机进气系统的试验研究[J].摩托车技术,1997(6):3-8.
[4]Mitianiec W,Bogusz A.Theoretical and Experimental Study of Gas Flow through Reed Valve in a Two-Stroke Engine[J].SAE Paper,1996(1):1802.
[5]钱兴华.无升程阀限制器的条状簧片阀开发[J].流体工程,1992,20(10):22 -26.
[6]高孝洪.内燃机工作过程数值计算[M].北京:国防工业出版社,1986.
[7]朱访君,吴坚.内燃机工作过程数值计算及优化[M].北京:国防工业出版社,1997.
[8]Dave A,Siddiqui A,Probst D,et al.Development of a Reed Valve Model for Engine Simulations for Two-Stroke Engines[J].SAE Paper,2004(1):1455.
[9]Battistoni M,Grimaldi C N,Baudille R,et al.Development of a Model for the Simulation of a Reed Valve Based Secondary Air Injection System for SI Engines[J].SAE Paper,2005(1):0224.
[10]吴丹青,丛敬同.压缩机簧片阀的数学模拟与设计[M].北京:机械工业出版社,1993.
[11]邓志勇.K157发动机进气系统单向阀的研究[D].济南:山东大学,2006.
[12]陈卓如,金朝铭,王洪杰,等.工程流体力学[M].北京:高等教育出版社,2004.
[13]刘铮,张杨军.内燃机一维非定常流动[M].北京:清华大学出版社,2007.

