理想状态下的双离合自动变速器升挡过程滑磨功分析
向永乐,杨翔宇,谢 明,吴张兵
(重庆理工大学车辆工程学院,重庆 400054)
双离合自动变速器(dual clutch transmission,DCT)结合了自动变速器(automatic transmission,AT)和机械式自动变速器(automated mechanical transmission,AMT)在舒适性和经济性方面的优势,且传动效率高,结构紧凑[1],同时消除了AMT在换挡过程中动力中断的缺点,实现了动力性换挡[2]。因此,双离合自动变速器具有广阔的发展空间和应用前景。按冷却介质可将其分为干式双离合自动变速器和湿式双离合自动变速器,前者是靠空气冷却而后者则是靠油液冷却。在频繁换挡过程中产生大量滑磨功以致摩擦片温度过高甚至失效仍为当前一大难题。本文就其升挡过程中离合器C1与离合器C2所产生的滑磨功进行探讨。
1 DCT结构及工作特点
图1所示为双中间轴式干式离合器1、2挡结构简图。该DCT系统有7个挡位,2个离合器C1,C2交替工作,其中离合器C1与1,3,5,7挡相连,离合器C2与2,4,6及倒挡相连。以1挡升2挡为例,升挡过程中,离合器C1逐渐分离,离合器C2逐渐结合,离合器C1与离合器C2有一段重叠工作时间,本文将其称为重叠量。根据不同的控制策略其重叠量也不相同。为论述方便,本文统称逐渐结合的离合器为结合离合器,逐渐脱开的离合器为脱开离合器。
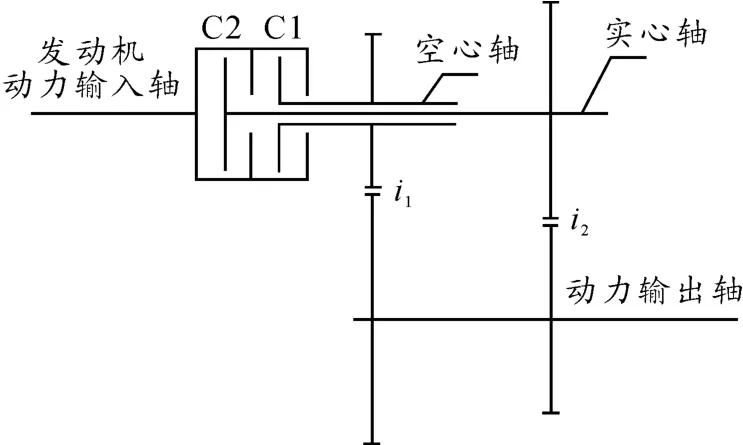
图1 双离合器1、2挡结构简图
2 控制策略的选定及所研究车型相关参数
不同的换挡控制策略决定了离合器的具体工作过程,在此以不同的重叠量制定3种典型控制策略进行分析探讨。离合器C1所能传递的力矩TC1与离合器C2所能传递的力矩TC2随时间t按如下3种控制策略变化(均以离合器C2开始结合为0时刻参考点)。

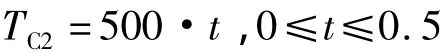
本文研究的车型有关参数如下:
1挡传动比(i1):3.764;
2挡传动比(i2):2.272;
驱动桥减速比(i0):4.437;
汽车总质量(W):1800 kg;
车轮滚动半径(RT):45 cm;
离合器转矩容量(Tmax):250 N·m。
为研究方便,本文作如下假设:
1)1挡升2挡发动机转速变化很小,本文假定其恒
定不变,传递的力矩可在极限范围内改变;
2)1、2挡车辆速度较低,忽略风阻的影响。
3 控制策略1
3.1 C1滑磨情况分析
根据滑磨功的计算公式可知,计算滑磨功须知道离合器主、从动盘转速差和传递力矩的大小以及滑磨的时间。因此,准确地判断离合器何时开始滑磨(本文将其称为始滑点)与何时停止滑磨(本文将其称为止滑点)至关重要。
在该种控制策略下离合器C1开始分离的同时,离合器C2就开始结合,C1在0.5 s完全分离,C2在0.5 s结合完毕。在离合器C1,C2重叠工作的过程中,C1与C2共同传递动力。由于离合器的转矩容量远远大于车辆1挡行驶时离合器C1从动盘上的阻力矩,加之离合器C2的助力作用,离合器C1并非一开始分离就立即进入滑磨状态。换言之,在1挡升2挡的过程中,存在这样一个阶段,即离合器C1已经开始分离却尚未进入滑磨状态,本文将该阶段称之为平衡态阶段。
在平衡态阶段,离合器C1所传递的力矩为静摩擦力矩,大小由离合器C2所传递的力矩与道路阻力矩共同决定,并非与其当前所能传递的力矩相等。因此在平衡态阶段有如下力矩平衡方程:

式(1)中:T'C1为离合器C1实际传递的力矩;TC2为离合器C2所能传递的力矩;MT1为1挡道路阻力矩,可用下式计算[3]:
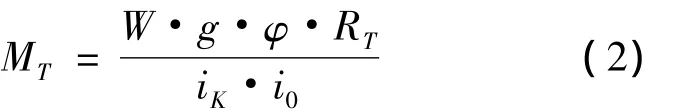
式(2)中:W为汽车总质量;g为重力加速度;i0为驱动桥减速比;ik为k挡传动比;φ为道路阻力系数,可用下式计算

式(3)中:f为滚动阻力系数,微型车、轻型车及轿车可取f=0.015;α为坡度角度。
由力矩平衡方程分析可知:当离合器C2单独传递的力矩尚不足以克服当前阻力矩时,离合器C1与离合器C2共同克服阻力矩以维持车辆当前行驶状态,车辆仍以1挡速度行驶。随着TC2的增加,离合器C1实际所传递的力矩T'C1逐渐减小。与此同时,离合器C1所能传递的力矩TC1也在减小。将有关数据代入平衡方程可得:当t=0.024 s时,T'C1=0,TC1=238 N。由此可知:经过0.024 s离合器C2单独所传递的力矩就已经足以平衡阻力矩,但此时离合器C1尚未完全分离,那么之后C1所传递的力矩将会变为阻力矩,会阻碍车辆加速,本文将其称之为反拖。经计算,当t=0.321 s时=TC1,也就是说离合器C1在0.321 s才进入滑磨状态,车辆的速度才开始改变,即t=0.321 s为C1的始滑点。那么在0.024~0.321 s内C1传递的力矩仍然为静摩擦力矩,且为起阻碍作用的反拖力矩。当C1完全分离时,C1就停止滑磨,即 t=0.5 s为 C1的止滑点。在0.321~0.5 s内C1从动盘角速度为

式(4)中:ω0为C1主动盘角速度;β1为C1从动盘角加速度,可由式(5)计算。

J1为汽车1挡当量惯量,J1可由式(6)计算。

在控制策略1下,离合器C1所产生的滑磨功(0.321 ≦ t≦ 0.5)为
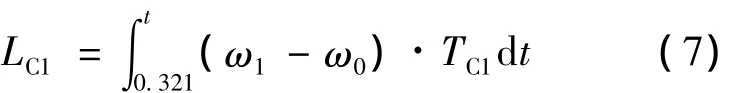
该控制策略下力矩与滑磨功随时间变化关系如图2所示。

图2 控制策略1力矩及C1滑磨功变化情况
3.2 C2滑磨情况分析
由于1挡传动比i1大于2挡传动比i2,离合器C2开始结合时其主、从动盘并不同速,则0时刻即为C2的始滑点。t=0.321 s时其从动盘才开始有角加速度,在0.321≤t≤0.5 s内 C2从动盘角速度为
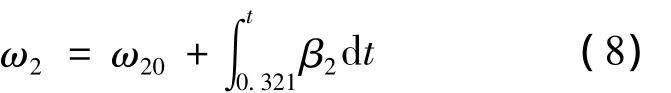
式(8)中:ω20为离合器C2从动盘初速度;β2为C2从动盘角加速度,可由式(9)计算。

式(9)中:MT2为汽车2挡道路阻力矩;J2为汽车2挡当量惯量。
由此可算得t=0.5 s时,离合器C2主、从动盘仍未达到同速,也就是说离合器C2已经结合完毕后,C2还未停止滑磨。由此可见:0.5 s以后,C2从动盘仍会继续加速;0.5 s到C2主、从动盘同速之前,其从动盘角速度为
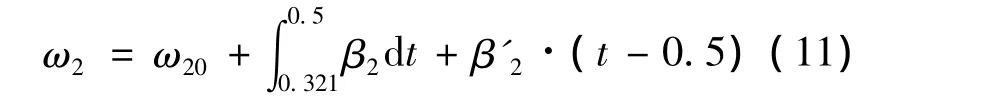
式(11)中β'2为C2从动盘0.5 s以后的角加速度,可由式(12)计算。
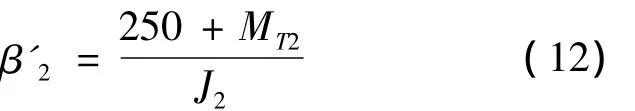
计算可得t=1.537 s为C2主、从动盘达到同速,即t=1.537 s为C2的止滑点。由以上分析可知:升挡过程中离合器C2的滑磨功须分3段分别计算,即

该控制策略下力矩与C2滑磨功随时间变化关系如图3所示。

图3 控制策略1力矩及C2滑磨功变化情况
4 控制策略2
与控制策略1的分析相同,在该种控制策略下,当离合器C2单独传递的力矩足以克服阻力矩时,离合器C1恰好完全分离,那么离合器C1在整个换挡过程产生的滑磨功为0。离合器C2的始滑点为t=0 s,止滑点为t=1.388 s。滑磨功仍分3个阶段来计算,升挡过程中总滑磨功为3段滑磨功之和,即

在该控制策略下力矩与滑磨功随时间变化的情况如图4所示。
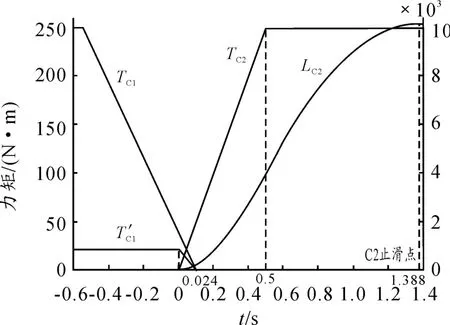
图4 控制策略2力矩及C2滑磨功变化情况
5 控制策略3
由力矩平衡方程可算得该控制策略下,t=0.009 s时,TC1=T'C1。也就是说当离合器C2单独传递的力矩还不足以克服阻力矩时,C1已进入滑磨状态。在此情况下,换挡过程中车速会出现下降,将会出现动力不足。C1始滑点为t=0.009 s,止滑点为 t=0.018 s,所产生的滑磨功为(0.009 ≦t≦ 0.018)
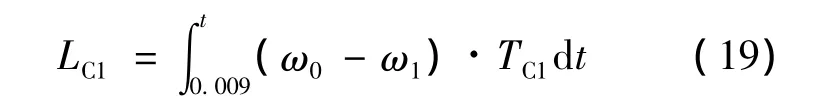
该控制策略下力矩与C1滑磨功随时间变化如图5所示。

图5 控制策略3力矩及C1滑磨功变化情况
C2的滑磨功须分为4个阶段来计算,即
第1 阶段:0≤t≤0.009 s
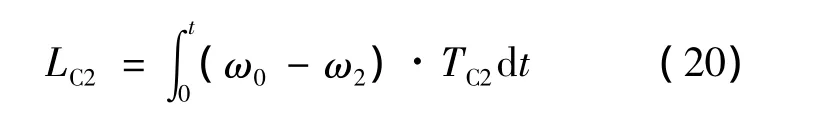
第2 阶段:0.009≤t≤0.018 s

第3 阶段:0.018≤t≤0.5 s

第4 阶段:0.5≤t≤1.388 s

该控制策略下力矩与C2滑磨功随时间变化的情况如图6所示。
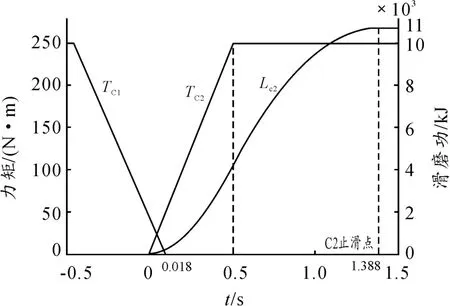
图6 控制策略3力矩及C2滑磨功变化情况
6 结束语
双离合自动变速器在升挡过程中,脱开离合器并非一开始减压就立即进入滑磨状态,其始滑点为其实际传递力矩等于当前可传递最大力矩时刻点。对于结合离合器,加压结束并不代表其滑磨结束,其止滑点只能以主、从动盘同速确定。
由3种控制策略仿真结果的分析可知:C1与C2适当的重叠量,可使脱开离合器在整个升挡过程中滑磨功为0,同时结合离合器滑磨功最小,因此从滑磨功方面考虑该控制策略最优;过大的重叠量会使脱开离合器造成反拖,会延长升挡时间,造成结合离合器产生较大的滑磨功,对C1、C2均不利;过小的重叠量会造成换挡过程动力不足,影响动力的连续性,车速将有下降。无论采取何种控制策略,升挡过程中脱开离合器产生的滑磨功都远远小于结合离合器产生的滑磨功。
后续的研究中,可根据实际发动机的特性曲线来建立模型,以实现更精确的计算。
[1]Kulkarni M,Shim T,Zhang Yi.Shift dynamics and control of dual clutch transmission[J].Mechanism and Machine Theory,2007.42(2):168 -182.
[2]Goetz M,Levesley M,Corolla D,Integrated powertrain control of gearshifts on twin clutch transmissions[C]//SAE Paper,2004.
[3]汽车工程手册.实验篇[M].北京:人民交通出版社,2000:153-154.
[4]Goetz M,Levesley M C,Crolla D A I.Dynamics and control of gearshifts on twin clutch transmissions[J].Proceedings of the Institution of Mechanical Engineers,Part D(Journal of Automobile Engineer),2005,219(D8):951-963.
[5]Dovat F.The revolutionary VW-Audi double clutch transmission[C]//Internet Document.Ge Anlin & Others.Research on Dynamic 3-parameter Gear-Shift Schedule.SAE 912488,1991.
[6]KULKARNI M,SHIM T,ZHANG Y.Shift dynamics and control of dual-clutch transmissions[J].Mechani-sm and Machine Theory,2007,42(2):168 -182.
[7]ZHANG Y,CHEN X,ZHANG X,et al.Dynamic modeling and simulation of adual-clutch automated lays-haft transmission[J].Journal of Mechanical Design,2005,127(2):302-307.
[8]AMIR I A,QIN Datong,LIU Zhenjun.A control strategy on starting up of vehicle with automatic manual transmissions[J].Information Technology Journal,2005,4(2):140-145.
[9]Kulkarni M,Shim T,Yi Zhang.Shift dynamics and control of dual~clutch Transmission Mechanism and Machine Theory[M].2006.2.
[10]Steff Schnetzler,Joakim Petersson and Paavo MUrtonen.Quality Assurance of Driver Comfort for Automatic Transmissions[C]//SAE Paper.[s.n.],2000.
[11]Persson J.Intergrated powertrain control—a literature survey on longitudinal vibrations,drivability aspects and,future challenges[Z].Master Thesis EX024/2003,Control and Automation Laboratory,Department of Signals and Systems,Chalmers University of Sweden,March 2004.
[12]葛安林,车辆自动变速理论与设计[M].北京:机械工业出版社,1991.
[13]金伦,程秀生,葛安林,等.AMT换挡过程的离合器控制[J].汽车技术,2006(1):11-13.
[14]吴光强,杨伟斌,秦大同.双离合器式自动变速器控制系统的关键技术[J].机械工程学报,2007,43(2):13-21.
[15]张哲诚.浅析双离合器自动变速系统模型的建立[J].中国高新技术企业,2010,18:200-201.
[16]屠海峰.基于DCT结构的动力换挡过程研究[D].重庆:重庆理工大学,2010.
[17]李瑜婷,赵治国,章桐.DCT变速器双离合器压力最优控制方法的仿真研究[J].中国机械工程,2010,21(12):1496-1501.
[18]杨昭.双离合器自动变速器动力学建模及仿真研究[D].长春:吉林大学,2007.

