动平衡实验机转子振动模态分析

高 阳，吕 硕，高 凯，任成东

GAO Yang，LV Shuo，GAO Kai，REN Cheng-dong

（北方民族大学 化学与化学工程学院，银川 750021）

0 引言

动平衡是旋转类产品生产、制造过程中必须解决的一个基本的共性问题，其优劣程度直接决定产品的工作性能、使用寿命，对产品的质量产生巨大的影响[1]。转子系统的非正常振动已成为引发事故的主要原因之一，因此转子动力学问题显得尤为重要[2,3]。动平衡机实验机转子的固有频率是影响动平衡机性能的重要参数，也是动平衡机支撑、驱动和传感器选型、设计的关键依据。因此，建立精确的转子-支撑系统动力学模型，并用ANSYS有限元对转子进行模态分析，研究设计参数对其影响，对动平衡实验机的设计改进有重要意义。

1 动平衡实验机工作原理

动平衡机的工作原理如图1所示。将待平衡的试件安放在框形摆架的支撑轮上，摆架的左端固结在工字型板簧中，右臂弹簧支撑。电机通过皮带带动试件旋转，当试件有不平衡的质量存在时，则产生离心惯性力使摆架绕工字型板簧上下周期性地振动，通过传感器可得振幅的大小。对于试件的不平衡量（或平衡量）的大小和方位的测量主要由差速器和补偿盘组成，差速器安装在摆架的右端，它的左端为转动输入端通过联轴器与试件联接，右端为输出端与补偿盘相联接。由于差速器是由齿数和模数相同的三个圆锥齿轮和一个蜗轮组成的周转轮系，当蜗杆不动时为定轴轮系，这时补偿盘的转速与试件转速大小相等方向相反；当试件与蜗杆都转动时为差动轮系，涡轮转速与试件同向转动时补偿盘减速，反之则加速。这样可以改变补偿盘与试件圆盘之间的相位角。

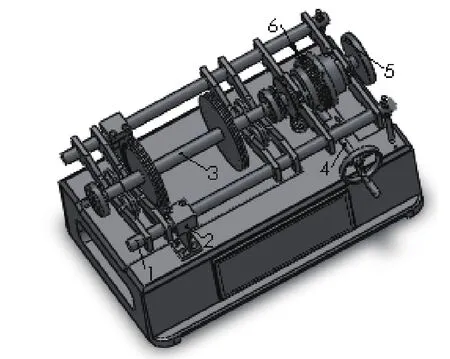
图1 动平衡实验机工作原理

2 转子动力学建模分析

转子材料的不均匀、制造误差、结构的不对称等诸因素导致转子在旋转时会产生离心惯性力组成一个空间力系，使转子动不平衡。当试件上有不平衡质量存在时，试件以角速度ω转动后产生离心惯性力 F＝mrω2，它可以分成垂直分力Fy和水平分力Fx，由于平衡机的工字型板簧和摆架在水平方向（绕y轴）抗弯刚度很大，所以水平分力Fx对摆架的振动影响很小可忽略不计。而在垂直方向上（绕x轴）的抗弯刚度小，因此在垂直分力产生的力矩的作用下，使摆架产生周期性的上下振动。因此，动平衡机可简化为自由度为2的线性受迫振动系统。设转子质量为M，对过质心且垂直于纸面的轴的转动惯量为J，不平衡量的质量分别为m1、m2，板簧和弹簧劲度系数分别为k1、 k2，转子与不平衡量的相对位置如图2所示。

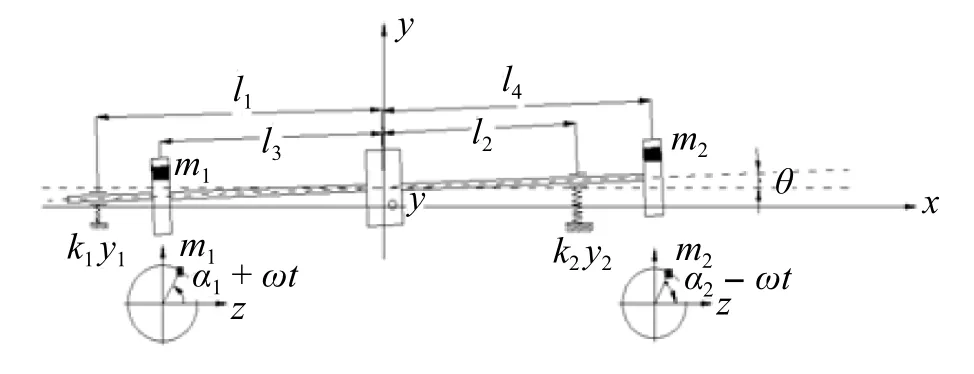
图2 转子-支撑振动系统动力学模型

设初始状态时系统水平，过质心建立坐标系。在运动的某一时刻，转子质心沿y轴方向的位移为y，转角为θ，板簧相对于初始位置的伸长量分别为y1、y2。可得转子运动微分方程：

1）解方程组4所对应的齐次方程组，可得y与θ的固有角频率p1、p2均为方程p4－（A1＋A2）p2＋A1A2－B1B2＝0的两正根：

3 转子的模态分析

1）转子模态前处理

根据转子试件的结构和精度要求，将其单元类型定义为Solid45单元。转子的材料为45，弹性模量200GPa，泊松比0.269，密度7810kg/m3。在建模的过程中将一些倒角等不影响分析结果的特征进行了简化和忽略[4]。将在Solidworks中创建好的实体模型保存为.x_t文件格式，利用ANSYS Connection for Parasolid接口将其导入到ANSYS中，使用利用Meshtool工具对其进行自由网格划分。尽量使划分的网格的粗细能够既满足分析的精度，又不至使模型太大，占用太多的计算机资源和求解时间。

在完成了有限元几何模型的建立和网格划分之后，便可以定义转子的边界条件和求解分析选项，对转子进行考虑预应力影响的模态分析。根据转子的工作条件，需要先进行有预应力的静力分析，然后在通过指定具体的分析选项进行有预应力的模态分析，求解转子的前几阶固有频率和相应的模态振型。滚轮近似为理想铰链约束，轴相对于摆架只能绕z轴转动，因此限制了x、y、z方向上移动和绕x、y方向的转动，同时转子试件左端皮带对轴主要产生的是预应力。其离心载荷是由于旋转产生的，因此需要在分析时指定转子的旋转速度。

2）转子静力分析

由于对转子模态的分析需要考虑离心力引起的应力对模态的影响，所以需要先对其进行静力分析，求解出离心力产生的应力，及其对刚度阵的影响，将结果写入数据库文件。

图3 变形后的总位移与未变形轮廓的比较

图4 转子Von mises等效应力分布

3）转子模态分析

对于转子的模态分析，模态提取方法为分块兰索斯法。它具有求解精度高、计算速度快等优点，适合对称特征值求解问题[5]。由于低阶模态对振动系统的影响较大，越是低阶影响越大，故进行结构的振动特性分析计算时通常取前5～10阶即可[6,7]。本文提取转子的前10阶模态，模态扩展阶数为10，并将ANSYS的Incl prestress effects（预应力效应）开启，在进行模态分析时ANSYS程序将会把前面静力分析中求解得到的离心力产生的应力对刚度的影响考虑进去。

通过计算，提取转子前10阶固有频率和相应振型，计算结果如表1所示。

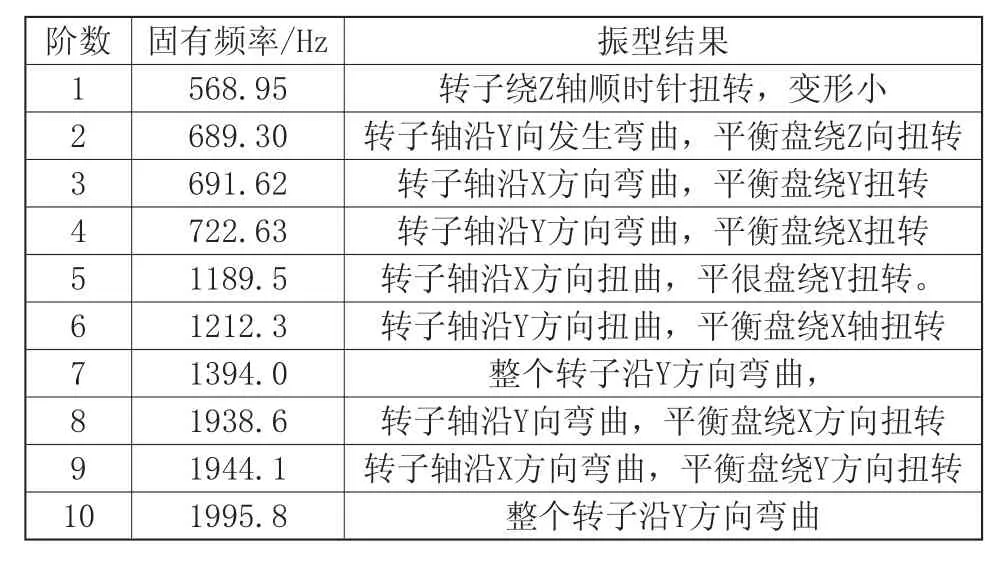
表1 转子固有频率及振型结果分析

由表1可以看出转子的前10阶固有频率在568.95～1995.8Hz之间，随着阶数增大，固有频率从小到大分布，且有些频率值很接近，这是由于转子结构和约束都是对称的，会出现振型和频率相接近但相位不同的情况。根据这些固有频率可以计算转子运动时的各阶临界速度。控制转子工作时的运动速度低于各阶临界速度一定的裕量，可使转子在工作过程中不会发生共振，保证包括转子在内的所有零、部件的安全稳定运行。

4 结论

在对动平衡实验机工作原理、转子动平衡的力学条件分析和动力学建模的基础上，利用有限元ANSYS软件，对转子进行了模态分析。研究了转子在有预应力影响下的前10阶固有频率和振型。通过动平衡机转子模态分析，通过转子的振型图和动态显示，直观地分析了转子动态特性，为更详细的动力学分析奠定了基础；为转子的振动控制、工作可靠性和使用寿命提供了理论依据；还为转子和摆架的结构优化设计了提供科学的参考数据，对后续整机结构动态改进设计，故障诊断提供重要的理论依据。

[1]王玮,刘亮.全自动动平衡机设计与动态分析[J].机电一体化,2008.03：45-54.

[2]宋兆泓.航空发动机典型故障分析[M].北京航空航天大学出版社，1993.

[3]袁平.WJ5系列发动机转子系统动力特性分析及故障机理研究[D].北京航天航空大学，2002.

[4]高耀东,郭喜平.ANSYS机械工程应用25例[M].北京：电子工业出版社，2007.

[5]王庆五,左昉,胡仁喜.ANSYS10.0机械设计高级应用实例[M].北京：机械工业出版社,2006：225-237.

[6]梁尚明,张均富,等.摆动活齿减速器箱体的有限元模态分析[J].机械设计,2003,（1）：14-17.

[7]梁尚明,罗伟,徐俊光,等.摆动活齿减速器的有限元模态分析[J].机械设计,2004,21（7）：14-16.