层合薄壁圆柱壳1∶1内共振研究
王延庆,梁 力,郭星辉,楼玲娜
(1.东北大学 应用力学研究所,沈阳 110004;2.东北大学 资源与土木工程学院,沈阳 110004)
薄壁圆柱壳被广泛应用于导弹、无人飞机、卫星外壳以及发动机等许多工程机械中。长期以来,学者们对于圆柱壳非线性振动的研究大多局限在模态相隔较远的情况[1-5],对于模态相隔较近的情况研究则不多。如果模态相距很近,那么相邻模态之间会产生耦合作用,对圆柱壳非线性振动的分析影响很大,这给此类问题的研究带来了一定的困难。在多自由度非线性系统中,当某些线性固有频率存在近似可通约关系时,振动系统的各阶模态强烈地耦合,能量不断交换,产生内共振。这将对工程中时常发生的超谐波与亚谐波共振产生重要影响,因此对内共振的研究有着重要的意义。白鸿柏[6]对密集模态间的非线性耦合作用做了初步研究,重点考察了密集模态组的整体表现。Thomas[7]利用扰动法分析了简谐激振下薄壁球壳的1∶1∶2内共振。Abe[8]采用打靶法,研究了夹支薄壁壳在两个反对称模态之间产生的1∶1内共振。在国内外的文献中,对于圆柱壳邻近模态内共振问题的研究还很少,此类问题仍需要更多的讨论与分析。
本文以电机升高片的层合圆柱外壳为研究模型,根据Donnell’s非线性简化壳理论,建立了系统的非线性振动方程,采用Galerkin方法对振动方程进行离散化。然后应用平均法,求解了系统包含两个相邻轴向模态的非线性振动响应,得到了反映复杂内共振的幅频特性曲线,表明系统存在1∶1内共振现象。最后与数值模拟进行了比较,并且得到了不同参数对层合薄壁圆柱壳复杂振动响应的影响。
1 振动方程
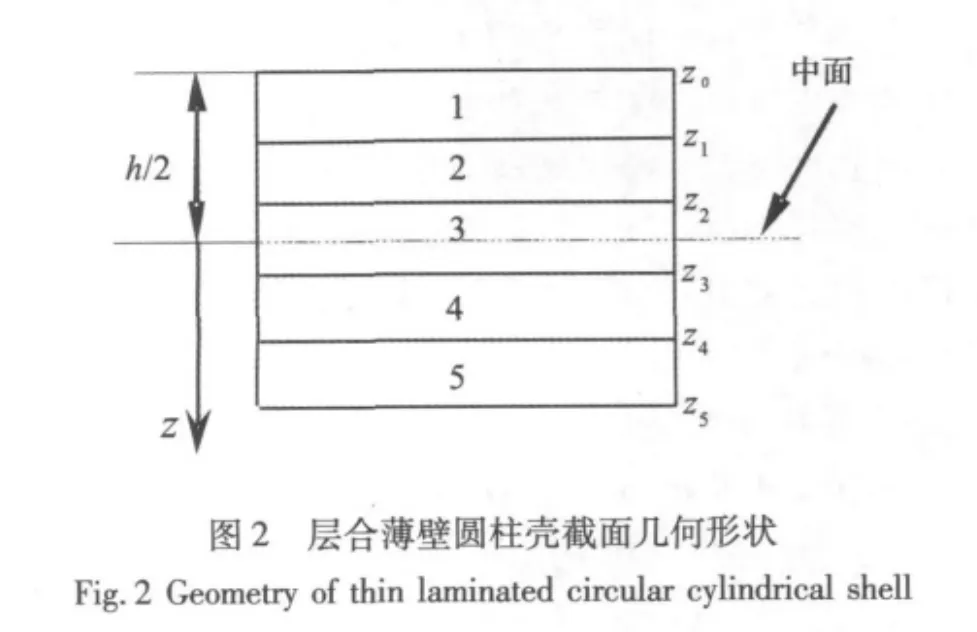
考虑一端固定,一端自由的层合薄壁圆柱壳模型(如图1),铺层材料为玻璃纤维布,它由玻璃纤维正交均匀交织而成,各单层的铺设角均为0°,截面几何形状如图2所示。

各向同性层合壳第k层的物理方程[9]:

其中Kx,Kθ为中面弯曲挠曲率,Kxθ为中面扭曲率,Qij为折减刚度矩阵,元素表达式为:

其中:Ek为第k层的弹性模量,μk为第k层的泊松比。
考虑层合圆柱壳的弹性模量随激振力频率变化而变化,两者有如下关系[10]:
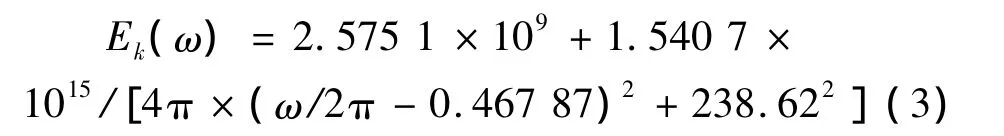
层合壳内力表达式为[9]:
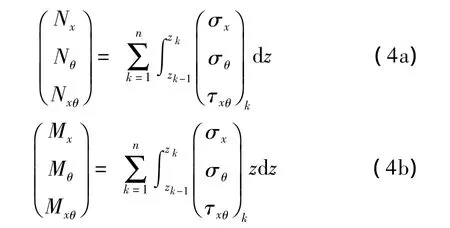
在几何方程中考虑非线性因素,利用薄壳理论及Donnell’s非线性简化壳理论得到层合薄壁圆柱壳非线性振动方程[11,12]:

具体表达式见附录(A1);c为阻尼系数;F(t)为外激振力,作用位置x0=0.34 m,θ0=π/24 rad,表达式为:

2 平均法过程
本文采用平均法来求解非线性振动方程。由文献[2]可知,周向模态N对圆柱壳非线性振动特性的影响很小,而轴向模态M影响相对较大,并且考虑到Donnell’s理论对N≥5较为精确,因此本文选择双模态(M=1,2;N=6)来分析圆柱壳的非线性动力学行为。位移形式如下:
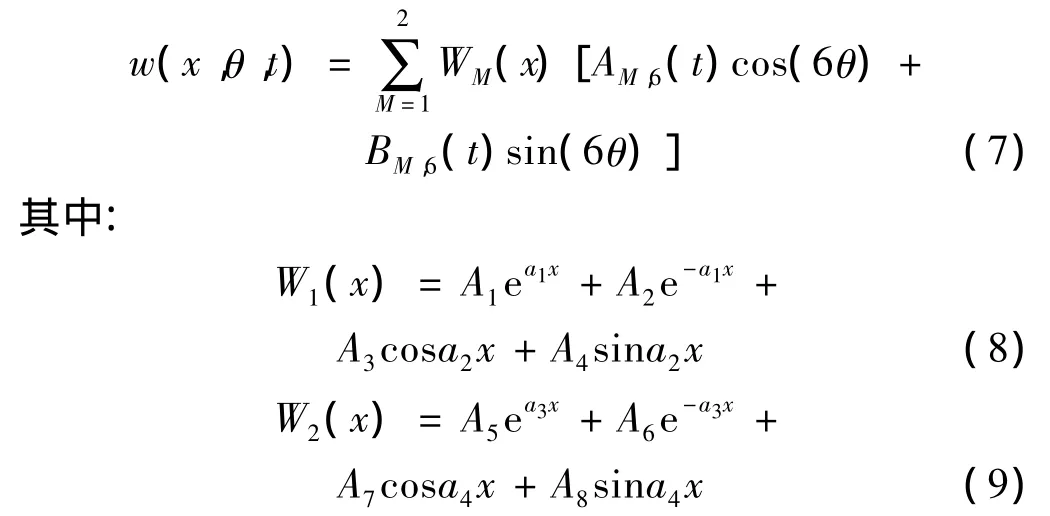
利用Galerkin法对振动方程(5)离散化,得到关于A1,6,B1,6,A2,6,B2,6的 4 个二阶非线性常微分方程 (见附录中A2)。
令:

则模态方程组(A2)可以用矩阵形式表示为:
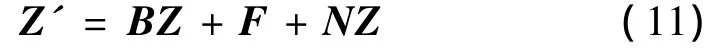
其中Z=[q1q2q3q4q5q6q7q8]T,B,F,N由模态方程组(A2)变形得到。
现构造矩阵:

则矩阵 Ω 与矩阵B具有相同的特征值 ± ω1,6i,± ω2,6i,设U为B的特征值所对应的特征向量组成的矩阵,V为矩阵Ω的特征值对应的特征向量组成的矩阵,则有下式成立:

设矩阵P=UV-1,则从方程(13)得到:

Z=Y,Y=PX,τ=ωt,并在式(11)等号两端前乘P-1,得到微分方程的标准形:

其中ε为小参数。
设激振力频率ω在某一固定频率ω0附近变化(这里 ω0= ω1,6),即:

式中σ是协调参数,表示外激励频率ω与ω0的接近程度。
将式(16)代入式(15),把1/(1+εσ)项展开成幂级数后,保留小参数ε的一次项,得:

引入振幅和相角ai,φi(i=1,…,4):

将式(18)中的xi(i=1,2,…,8)对 τ求导并代入式(17),然后对其应用平均法原理,则可以得到平均方程。为求平均方程定常解,令所有一阶导数项等于零,可以得幅频方程如下:
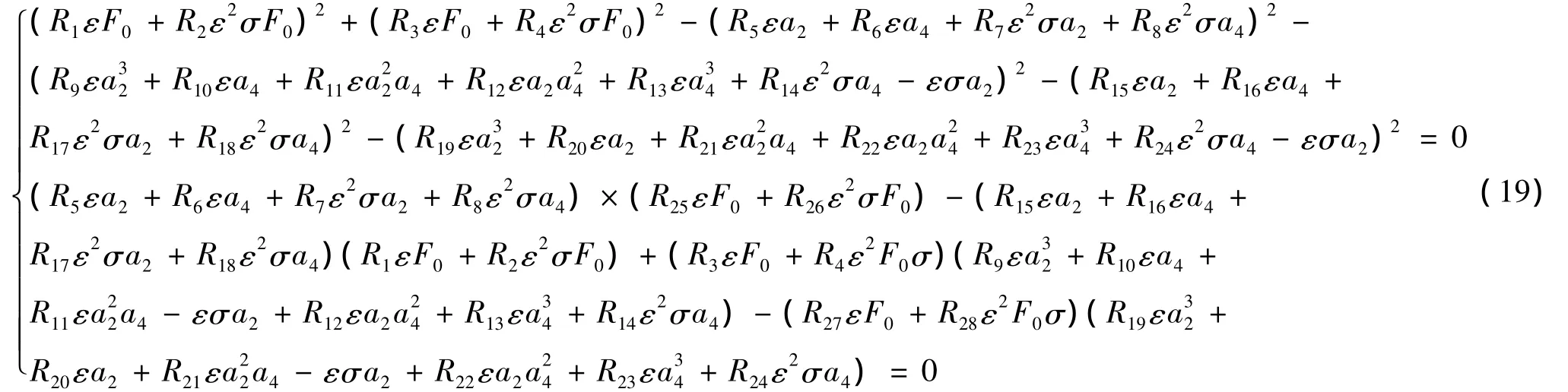
其中Ri(i=1,2,…,28)为平均化产生的积分系数。
3 近似解析解
圆柱壳的几何及材料参数如下:长度L=0.34 m,中面半径R=0.090 75 m,层数n=5,单层厚hk=0.000 1 m,泊松比 μk=0.3,壳体密度 ρk=1 951 kg/m3,两阶固有频率 ω1,6=174.27 × 2π rad/s,ω2,6=179.52×2π rad/s。可以发现两阶固有频率非常接近,因此系统可能存在1:1内共振。根据方程(19)得到稳态解的幅频特性曲线,采用李雅普诺夫一次近似理论判断稳态解的稳定性,结果如图3所示。其中实线表示稳定的周期解,虚线表示不稳定的周期解。

图3 幅频特性曲线 (F0=10 N,c=24.7 Nsm-3)Fig.3 Frequency-response curves for F0=10 N,c=24.7 Nsm-3

图4 时间响应(F0=10 N,c=24.7 Nsm-3,ω =177.8 ×2π rad/s)Fig.4 Response curves for F0=10 N,c=24.7 Nsm-3,ω =177.8 ×2π rad/s
本文考虑外激振力在第一阶固有频率附近。从图3中看出,不仅系统的第一阶模态被激励起来,第二阶模态也同样被激励,幅频特性曲线出现多个解支,并且表现出硬特性。当通过σ=0时,两阶模态表现出不同的变化趋势,其中第一阶模态解支A对应的幅值开始变小,而第二阶模态解支A对应的幅值则相反,会继续增大。当σ增加到1.34时,开始出现多值性,出现解支B,B的两条分支都随着σ的增大而增大,并且在σ=1.34~5区间内第二阶模态出现了封闭的环解。之后随着σ的增加,两阶模态都陆续出现两个分支C和D,当第一阶模态处于上半支时,第二阶模态跳跃到下半支,它们的变化趋势相反。图3中幅频曲线的变化特点说明,在第一阶固有频率附近,由于两阶模态频率十分接近,它们之间存在强烈的耦合,两阶模态彼此影响牵制,能量在它们之间传递,产生了1∶1内共振。而立方非线性带有内共振的系统,能量可以很容易地从高阶模态传输到低阶模态,反之则不然[13],因此第一阶模态响应大于第二阶模态响应。
从图4的时间响应中可以更直观地看出两阶模态间的能量交换,在恒定的激励作用下,模态响应值不确定,可以在不同解支之间跳跃,当第一阶模态的响应较大时,第二阶模态的响应较小,反之亦然。
图5给出近似解析解与数值解的比较,其中数值解采用4阶Runge-Kutta方法得到。从图中可以看出,二者变化趋势及拐点的位置都相同,只是幅值上有一些偏差。这主要是由于复合材料动态弹性模量随激振力频率而变化[10],数值解中考虑了这种变化,而在解析法中无法考虑这种关系,仅取激励频率等于第一阶固有频率时的弹性模量来近似,所以造成了一些误差。但这不影响我们对系统动力学行为的定性分析。
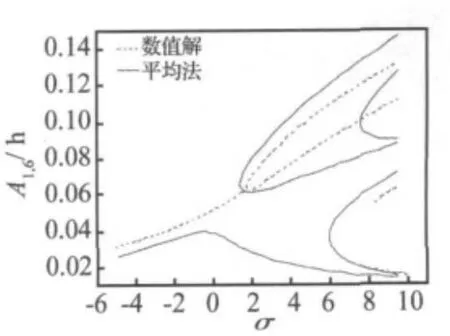
图5 平均法与数值法比较(F0=10 N,c=24.7 Nsm-3)Fig.5 Frequency-response curves got by averaging method and Runge-Kutta method(F0=10 N,c=24.7 Nsm-3)

图6 不同激励幅值下的幅频特性曲线(c=24.7 Nsm-3)Fig.6 Frequency-response curves of different excitation amplitude for c=24.7 Nsm-3
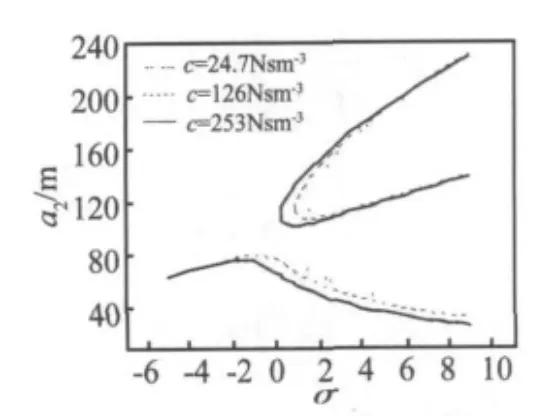
图7 不同阻尼系数下的幅频特性曲线(F0=20 N)Fig.7 Frequency-response curves of different damping coefficient for F0=20 N
4 不同参数的影响
本文以第一阶模态为例给出不同参数对系统复杂振动响应的影响。图6给出了不同激励幅值下系统的幅频特性曲线。从图中可以看出,随着激励幅值的增大,幅频曲线的解支有所减少 (如F0=10 N对应的幅频曲线比F0=5 N对应的幅频曲线少了一个半椭圆形的解支),但是系统的硬特性增强。
图7为不同阻尼系数下的幅频特性曲线,可以看出阻尼对响应的影响比激励的影响小得多,振动响应对阻尼不敏感,这主要是由复合材料自身的特性所决定的。
5 结论
本文根据Donnell’s非线性简化壳理论建立了一端固定,一端自由的层合薄壁圆柱壳的动力学方程,应用平均法求解了系统包含两个相邻轴向模态的非线性振动响应,得到以下结论:
(1)由于所选的两阶模态频率相距比较近,它们之间存在强烈的耦合,彼此影响牵制,能量在两阶模态之间相互传递,因此幅频特性曲线反应出系统内部存在1∶1内共振。
(2)由同种材料铺设而成的圆柱壳的幅频曲线表现出硬特性。随着激振力幅值的增大,系统的硬特性变得更明显,同时幅频曲线的解支有所减少;阻尼对振动响应的影响很小,说明玻璃纤维布层合圆柱壳的响应对阻尼不敏感。
[1]Wouters C R.Large amplitude free vibrations of shallow spherical shell and cylindrical shell[J].International Journal of Nonlinear Mechanics,1985,20(2):69-78.
[2]王延庆,郭星辉,常海红,等.旋转薄壁圆柱壳振型进动的非线性振动特性[J].固体力学学报,2009,30(3):267-279.
[3]Huang K H,Dasgupta A.A layer-wise analysis for freevibration of thick composite cylindrical-shells[J].Journal of Sound and Vibration,1995,186(2):207-222.
[4]Ganapathi M,Kvaradan T.Nonlinear free flexural vibrations of laminated circular cylindrical shells[J].Composite Structures,1995,30(1):33-49.
[5]Amabili M, PellicanoF, PaidoussisM P. Non-linear dynamics and stability of circular cylindrical shells containing flowing fluid.Part III:Truncation effect without flow and experiments[J].Journal of Sound and Vibration,2000,237(4):617-640.
[6]白鸿柏,张培林,陈振藩.密集模态组间非线性相互作用的初步研究[J].航空学报,2000,21(5):458-461.
[7]Oliver T,Touze C,Chaigne A.Non-linear vibration of freeedge thin spherical shells:modal interaction rules and 1∶1∶2 internal resonance[J].International Journal of Solids and Structures,2005,42(11-12):3339-3373.
[8]Abe A,Kobayashi Y,Yamada G. Nonlinear dynamic behaviors of clamped laminated shallow shells with one-to-one internal resonance[J].Journal of Sound and Vibration,2007,304:957-968.
[9]沈观林,胡更开.复合材料力学[M].北京:清华大学出版社,2007.
[10]李 健,郭星辉,郭明涛,等.复合材料薄壁圆柱壳动态弹性模量的研究[J].东北大学学报(自然科学版),2008,29(12):1770-1773.
[11] Soedel W.Vibrations of Shells and Plates[M].New York:Marcel Dekker;1981.
[12] Wang Y Q,Guo X H,Li Y G,et al.Nonlinear traveling wave vibration of a circular cylindrical shell subjected to a moving concentrated harmonic force[J].Journal of Sound and Vibration,2010,329(3):338-352
[13]周纪卿,朱因远.非线性振动[M].西安:西安交通大学出版社,1998.
附录:
非线性项:


模态方程组:

其中:A1,6,B1,6,A2,6,B2,6为时间t的函数,Si,Hi(i=1,2,…,15)为积分系数。

