轮胎多边形磨损的发生机理及其影响因素分析

李 勇，左曙光，杨宪武，吴旭东

(同济大学 汽车学院，上海 201804)

在所有的轮胎磨损形式中，非正常磨损对轮胎使用寿命的影响最大，而偏磨损又是轮胎非正常磨损的主要形式，其中以从动轮的多边形磨损最为典型。这种磨损可导致轮胎提前报废，造成爆胎等严重威胁汽车行驶安全的事故。

近年来，国内外关于轮胎磨损机理的研究有了大量的报道［1-4］，而有关多边形磨损的研究却鲜有报道。日本Sueoka［5］研究小组将轮胎多边形磨损归纳为滚动接触系统，认为胎面磨损引起的垂向自激振动是其产生的根源，并根据实验结果提出了轮胎多边形磨损边数的计算公式，即多边形磨损的边数近似等于轮胎的固有频率和车轮转动频率之比，但是该研究只考虑了垂向自由度，并没有从根本上揭示轮胎多边形磨损的发生机理，不能合理地应用到汽车轮胎磨损研究中。本文正是基于这样的背景，从轮胎与路面之间相互作用的特征出发，在侧向上探讨轮胎多边形磨损的发生机理，采用基于能量法并依据实验数据修正得到的胎面单元侧向刚度计算公式，建立基于胎面自激振动的轮胎多边形磨损动力学模型，并分析车速、载荷及轮胎定位参数(前束角)对轮胎磨损的影响。

1 数学模型

轮胎磨损是一个长期复杂的过程，为了便于分析，本文假设轮胎与路面之间只有两种类型的磨损，一种是轮胎与路面之间的正常磨损，即周向均匀磨损;另一种是由于胎面扰动而造成的周向不均匀磨损。当胎面发生侧向振动时，胎面在均匀磨损的同时还存在扰动磨损，此时胎面的磨损为均匀磨损和扰动磨损的叠加，导致轮胎磨损的周向不均匀，即可能产生轮胎多边形磨损现象。为了分析轮胎的侧向振动，首先将胎面离散化，简化为若干集中质量体，取接地质量块作为研究对象，其与整个轮胎的连接方式如图1所示，图中Ks和Cs分别为胎面的侧向刚度和侧向阻尼，m为胎面质量。

图1 胎面-路面自激振动理论模型Fig.1 The theoretical model of self-excited vibration for tread-pavement

由于本文主要分析轮胎的侧向振动，因此胎面侧向刚度Ks的确定显得尤为重要。这里我们采用能量法分析Ks，选取胎面单元的长宽高分别为a、b和h。胎面单元在垂向载荷和侧向载荷的作用下将发生变形，设侧向载荷和侧向变形分别为Q和λ，应用能量法可以得到［6］:

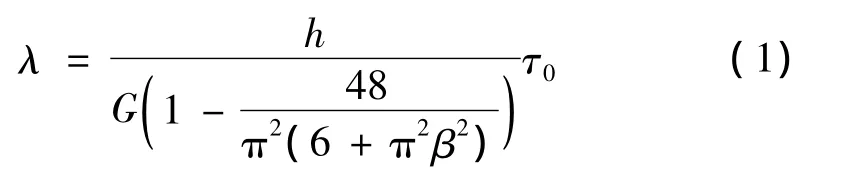
式中G为胎面橡胶的剪切弹性模量，β为单元长高比，τ0=Q/(ab)为作用在胎面单位上表面的平均剪应力。

由上式可得到胎面单位的侧向刚度计算公式:

由于胎面的侧向刚度受很多因素的影响，其中尤以垂向载荷的影响较大，按照式(2)计算所得的刚度与实际有一定差别，下面我们通过与实验结果对比对计算公式进行修正。本文中选取轮胎接地质量块为胎面单元，并忽略接地胎面与轮胎侧向刚度的区别。根据课题组前期实验，所用轮胎型号为195/65R15，表1和表2分别给出了车辆轮胎气压为280 kPa时不同垂向载荷下的接地印迹和侧向刚度［7］。

表1 不同垂向载荷下接地印迹数据表Tab.1 The data table of lateral stiffness at different vertical load

表2 不同垂向载荷下侧向刚度数据表Tab.2 The data table of lateral stiffness at different vertical load

根据表1，可以得到接地印迹与垂向载荷的拟合公式为:

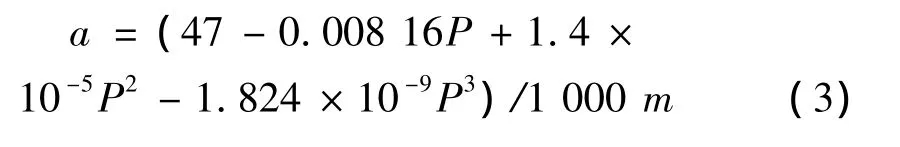
将式(3)、式(4)代入式(2)，则可以得到不同垂向载荷下胎面单元侧向刚度的计算公式。由式(2)计算得到的侧向刚度与表2中的实验结果存在很大的差别，因此需要进行修正，式(5)给出了修正后的计算公式。

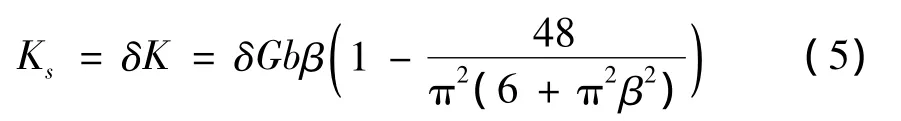
式中 δ=1.177 7-2.569 ×10-4P-1.075 ×10-9P2+3.858×10-12P3为修正系数。

在汽车前进过程中，由于前束角的存在，轮胎在侧向方向上会获得一定的速度输入。设前束角为θ，将汽车前进速度V分解到侧向上，则得到轮胎在侧向上相对于地面的线速度Vb:

在模型中，胎面振动能量的输入来源于胎面与地面之间持续不断的摩擦力作用，即两者之间的相对速度变化是激励源。为了便于分析，将轮胎与地面间的平动简化为皮带轮的转动。简化后的模型如图2所示。

图2 胎面摩擦振动模型Fig.2 The friction vibration model of tread

设胎面质量块m在皮带上相对于初始位置(即弹簧及阻尼器不受力时的位置)的位移为s，质量块m与皮带间的相对速度Vr为:

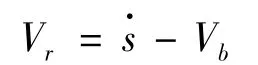
则胎面质量块m侧向振动的动力学方程如下:

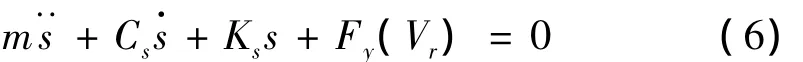
式中Fy(Vr)为胎面所受的侧向力。

在胎面-路面模型中，摩擦特性的描述一直是轮胎力学建模的重点和难点，它直接关系到模型的精度。本文采用由 de Wit Carlos等［8］提出的摩擦模型 -LuGre摩擦模型。模型的表达式如下:

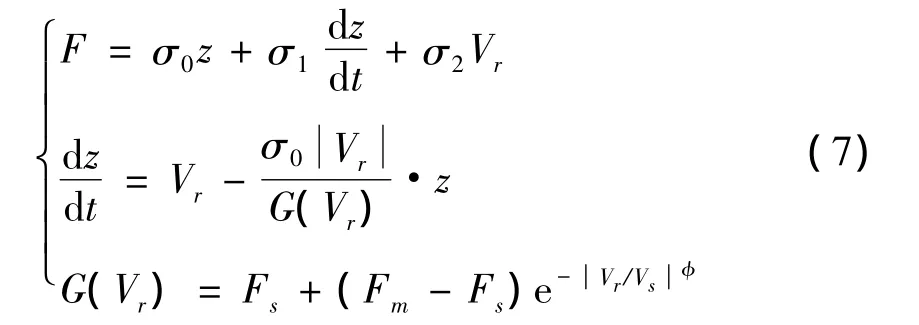
式中σ0和σ1分别为刷毛刚度系数和阻尼系数，这里可以认为与胎面的刚度和阻尼是相同的;σ2为相对粘滞阻尼系数;z为刷毛的弹性变形量;Vs为稳态摩擦特性中的Stribeck速度;φ为稳态摩擦特性中的Stribeck指数;Fm=P·μm·sinα为最大静摩擦力;Fs=P·μs·sinα为滑动摩擦力;μm为最大静摩擦系数;μs为动摩擦系数;α为轮胎的滑移角，滑移角包括轮胎的前束以及轮胎侧向弹性侧偏造成的轮胎与前进方向的夹角，本文忽略轮胎侧偏造成的偏角，认为滑移角和前束角θ是相同的。

综合以上分析，并忽略轮胎与地面间的相对粘滞，即σ2=0，则可得到系统的振动微分方程

对上式进行无量纲化，引入变化

其中Ks0=7.3×105N/m，L0为单位长度。

则化简后得到无量纲方程为

其中无量纲参数为:

将式(9)化为一阶微分方程组:

该方程刻画了轮胎侧向运动的演化过程，其解对应系统某种状态，如平衡点对应运动的稳定状态;周期解表示系统偏离原来的运动状态，按照一定的频率周期性变化，即产生自激振动，此时胎面受到的磨损将为均匀磨损和扰动磨损的叠加，可能产生轮胎多边形磨损现象。

由李雅普诺夫稳定性理论可知，当系统的最大李雅普诺夫指数为负值时，系统处于稳定运动状态;当最大李雅普诺夫指数出现零值时，系统可能通过Hopf分岔失稳，从而导致周期振荡，即发生自激振动，因此可以说轮胎的自激振动是一种由系统Hopf分岔引起的稳定周期振动现象。系统的稳定临界条件将参数空间划分为不同的区域，当参数达到临界分岔点时，系统将失去了稳定性，出现稳定的周期解，即可能导致轮胎多边形磨损现象的发生。由于系统比较复杂，理论分析有一定难度，因此下面我们通过数值模拟来确定能够引起胎面自激振动的参数范围。

2 数值模拟

造成轮胎多边形磨损的潜在因素很多，可能是车辆的动态性能、定位参数、悬架和道路情况等方面的原因，也可能是轮胎的结构参数、形状参数、胎面形式和胎压等原因造成的。考虑轮胎多边形磨损的发生特征，可以发现汽车行驶速度、整车质量(反映在胎面上即为垂向载荷)和轮胎前束角对磨损的影响很大，因此本文分别以车速、前束角和垂向载荷为分岔参数，探讨系统动力学行为的变化，确定可能导致轮胎发生多边形磨损的参数区域。

取m=0.3 kg，Cs= σ1=10 Ns/m，Vs=0.2 m/s，φ =1.8，μm=0.9，μs=0.7。

2.1 车速对轮胎磨损的影响

给定轮胎前束角θ=0.28°，垂向载荷P=4 000 N，图3给出了系统随参数γ，即随车速变化的分岔图。

图3 系统随γ变化的分岔图Fig.3 The bifurcation diagram of the system with the variation of γ

从分岔图可以看出，系统在γ较小时处于稳定状态，表明车速较小时胎面不能产生自激振动。随着γ的增大，即车速的增加，稳定的平衡点在 γ =0.974时失去稳定性，由Hopf分岔导致周期振荡，即胎面产生自激振动。随着γ的进一步增大，系统在 γ=1.961时再次趋于稳定状态。因此我们可以得到，γ在0.974～1.961的范围内系统为周期运动，对照前文中的无量纲变化过程，则车速处于70.128 km/h～141.192 km/h时胎面能产生自激振动，即当汽车以中高速行驶时可能导致轮胎多边形磨损产生，这与经常行驶在高速公路上的汽车更易出现多边形磨损的实际情况是一致的。

2.2 轮胎前束角对轮胎磨损的影响

在轮胎定位参数中，前束角是影响轮胎多边形磨损的一个重要因素，因此有必要分析前束角对轮胎磨损的影响，从而通过调整轮胎前束角避免或减少轮胎多边形磨损发生。通过以往的研究发现，当汽车在高速公路上行驶时，轮胎发生多边形磨损的概率特别高，故设定γ=1.5(即车速为108 km/h)和垂向载荷P=4 000 N，图4给出了汽车高速行驶时系统随θ变化的分岔图。

图4 系统随θ变化的分岔图Fig.4 The bifurcation diagram of the system with the variation of θ

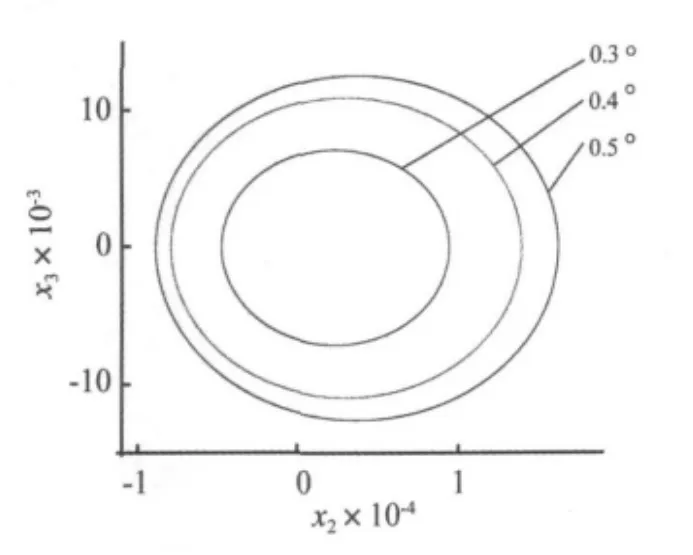
图5 不同前束角时系统的相图Fig.5 The phase maps of system at different toe-in angle

图6 系统随P变化的分岔图Fig.6 The bifurcation diagram of the system with the variation of P

从图4可以得到，当轮胎前束角处于0.247～0.558时胎面能产生自激振动，因此在设定轮胎定位参数时，可以调整前束角使其避开这一范围以避免或减少轮胎多边形磨损发生。并且可以发现，随着θ的增大，系统的振荡范围是不断变大的(见图5)，表明随着前束角的增加，胎面的自激振动越来越剧烈，即发生多边形磨损的可能性将增大，这也符合轮胎多边形磨损的发生特征——多边形磨损在车轮定位中当前束角过大时容易发生。

2.3 垂向载荷对轮胎磨损的影响

从上文我们得知，垂向载荷对胎面的侧向刚度及胎面所受侧向力都着重要的影响，从而将影响胎面的侧向运动状态，因此有必要分析垂向载荷对轮胎磨损的影响。给定车速V=108 km/h和轮胎前束角θ=0.28°，图6给出了系统随垂向载荷P变化的分岔图。

从上图可以看出，当胎面所受垂向载荷大于3 525 N时系统由Hopf分岔失稳而导致周期振荡，即胎面能产生自激振动，且随着P的增大，系统的振荡范围是不断变大的(见图7)，胎面的自激振动越来越剧烈，即发生多边形磨损的可能性将增大。随着垂向载荷的进一步增大，系统在7 365 N时再次趋于稳定状态。因此我们得出当车辆超载时轮胎发生多边形磨损的机率将增大，载荷过大是导致轮胎多边形磨损的一个可能因素。

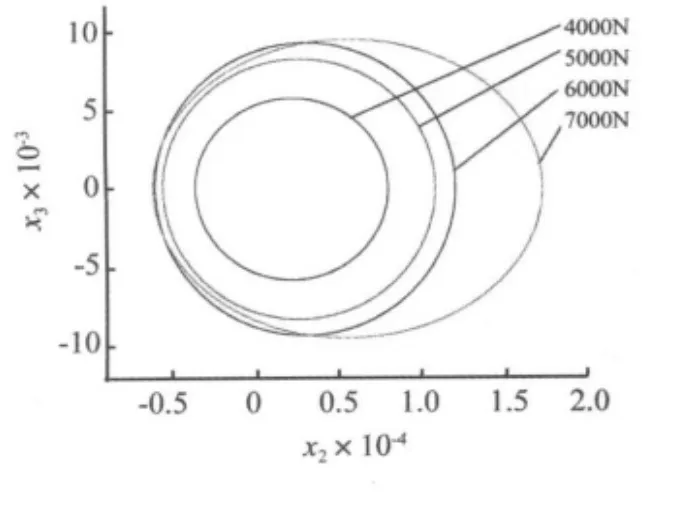
图7 不同垂向载荷时系统的相图Fig.7 The phase maps of system at different vertical load

3 结论

本文从轮胎与路面之间相互作用的特征出发，在侧向上探讨轮胎多边形磨损的发生机理，采用基于能量法并依据实验数据修正得到的胎面单元侧向刚度，建立了基于胎面自激振动的轮胎多边形磨损动力学模型，并通过数值仿真分析了车速、载荷及轮胎定位参数(前束角)对轮胎磨损的影响。得到如下结论:

(1)轮胎多边形磨损为胎面均匀磨损和扰动磨损叠加引起的周向不均匀磨损，其发生与胎面的侧向振动有关，此观点能较好地解释轮胎多边形磨损现象。

(2)以李雅普诺夫稳定性理论为基础，指出轮胎的自激振动是一种由系统Hopf分岔引起的稳定周期振动现象。当参数达到临界分岔点时，系统将失去了稳定性，出现稳定的周期解。

(3)通过仿真得出当车速在 70.128 km/h～141.192 km/h之间时，胎面将会发生自激振动，从而可能导致轮胎多边形磨损现象，这与经常行驶在高速公路上的汽车更易出现多边形磨损的实际情况一致。

(4)为避免汽车高速行驶时发生轮胎多边形磨损，通过仿真得到了引起胎面自激振动的轮胎前束角范围，从而可以通过调整前束角使其避开这一范围以避免或减少轮胎多边形磨损发生;同时还发现，胎面自激振动的幅值和速度随着前束角的增大而增大，表明前束角过大时更易导致多边形磨损现象。

(5)当胎面所受垂向载荷大于3 525N时胎面将发生自激振动，表明载荷过大是导致轮胎多边形磨损的一个可能原因。

［1］ Fujijawa T，Uchiyama Y，Yamaguchi I.Tire model to predict treadwear［J］.Tire Science and Technology，1999，27(2):106-125.

［2］ Fujijawa T，Yamazaki S，Uchiyama Y.Tire wear caused by mild slip of tread ［J］.Rubber Chemistry and Technology，1997，70(4):572-583.

［3］黄海波，彭 为，靳晓雄，等.复合式后悬架轮胎偏磨损动态仿真［J］.同济大学学报，2006，34(11):1530-1533.

［4］李文辉，魏 宏，吴光强.轮胎磨损解析研究［J］.汽车技术，2002，6:13-15.

［5］ Sueoka A，Ryu T，Kondou T，et al.Polygonal wear of automobile tire［J］.JSME，1997，40(2):210-217.

［6］王吉忠，庄继德.轮胎胎面单元表观刚度计算［J］.农业工程学报，2000，16(2):28-31.

［7］周震华.基于摩擦自振的扭杆梁式悬架和轮胎系统建模与分析［D］.上海:同济大学，2008.

［8］ Canudas D W C，Olsson H，Astrom K J，et al.A new model for control of systems with friction［J］.IEEE Transactions on Automatic Control，1995，40(3):419-425.