基于ASEGMF的旋转机械振动信号降噪方法研究
张文斌,王鸿钧,滕瑞静,李俊生
(1.红河学院 工学院,云南 蒙自 661100;2.浙江大学 机械工程学系,杭州 310027)
工业现场采集到的振动信号往往包含大量的噪声干扰,能否有效地降低噪声、提高信噪比,是进行机械设备早期故障诊断的关键。近年来随着小波分析与奇异值分解在信号降噪中的应用[1,2],信号降噪技术取得了一定的进展。但是小波降噪和奇异值分解分别因为阈值选取和奇异值选择的不确定性而影响了降噪效果[3]。
数学形态学[4]是以集合论为基础发展起来的有别于基于时域、频域的数学方法。文献[5]已将形态滤波器用于旋转机械振动信号的降噪,文献[3,6]也引入广义形态滤波器用于振动信号降噪。但是由于结构元素选择的随机性,在实际运用中如何自适应地确定结构元素的尺寸是目前形态学研究的热点。
本文根据旋转机械振动信号的特点,根据信号的局部峰值特征提出了一种基于自适应结构元素的广义形态滤波方法,将一小一大的自适应结构元素级联而成广义形态滤波器,通过仿真和实测信号的分析,得到了比形态滤波器更好的降噪效果。
1 基本形态变换及其广义形态滤波器
形态变换一般分为二值形态变换和多值(灰度)形态变换。由于在振动信号中一般只涉及一维信号,本文只限于一维离散情况下的多值形态变换,包括腐蚀、膨胀、形态开和形态闭,以及形态开、闭的级联组合。
定义1:设f(n)为定义在F={0,1,…,N-1}上的离散函数,g(n)为定义在G={0,1,…,M-1}上的离散函数,且N≥M,这里f(n)为输入序列,g(n)为结构元素,则f(n)关于g(n)的腐蚀和膨胀分别为
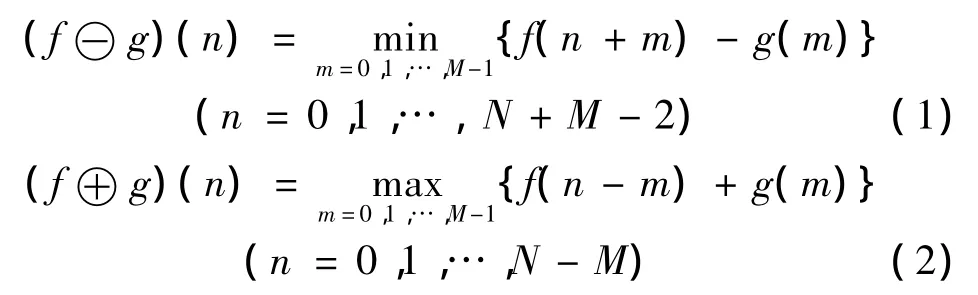
式中:⊖和⊕分别表示腐蚀和膨胀运算,f(n)关于g(n)的形态开和形态闭分别定义为:
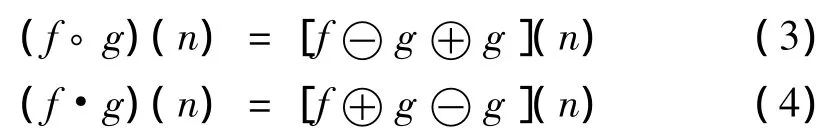
式中:◦和·分别表示形态开和形态闭运算,由于噪声通常表现为信号上叠加窄的“毛刺”,即一些很尖的“峰”和很低的“谷”,形态开可以削去“峰”,形态闭可以填平“谷”[7]。
为了同时去除信号中的正、负噪声干扰,通常采用形态开、闭的级联形式。Maragos[8,9]利用相同尺寸的结构元素,通过开、闭运算的级联组合,定义了如下的形态开-闭(open-closing)和闭-开(close-opening)滤波器。
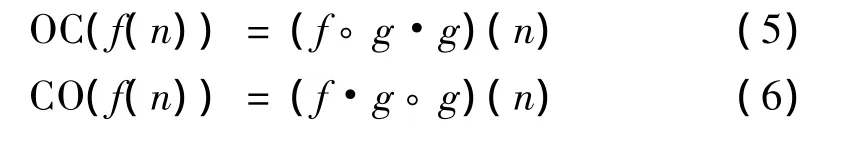
这样定义的滤波器具有开闭运算的所有性质,可以同时去除信号中的正负脉冲干扰。对于形态开-闭滤波器而言,首先进行的开运算在去除正脉冲噪声的同时,增强了负脉冲噪声,如果再采用相同的结构元素进行闭运算,就不能有效地去除全部的负脉冲噪声;同样,采用相同结构元素的形态闭-开滤波器也不能有效地去除全部的正脉冲噪声。因此,对上述两种滤波器进行改进,选用不同尺寸的结构元素,令后级结构函数的宽度大于前级结构函数,构造了广义形态开-闭和形态闭-开滤波器[10-12]。
定义2:设f(n)为定义在F={0,1,…,N-1}上的离散函数,两个结构元素分别为g1(n)(n∈G1)和g2(n)(n∈G2),且G1⊂G2,则广义的形态开 -闭和形态闭-开滤波器分别定义为:
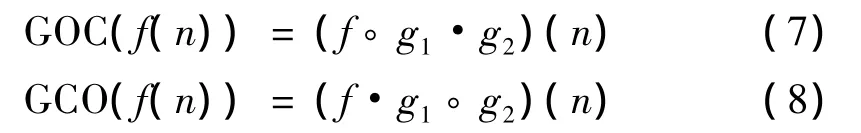
由于开运算的收缩性导致开-闭滤波器的输出偏小,闭运算的扩张性导致闭-开滤波器的输出偏大,因此信号在滤波过程中存在统计偏移现象,单独使用它们并不能取得良好的滤波效果[10]。为了有效去除振动信号中的各种噪声干扰,本文采用广义组合滤波器的输出为[6]:
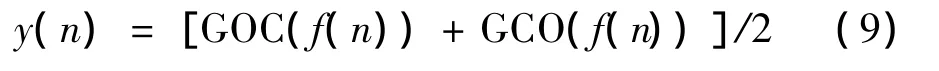
2 自适应结构元素广义形态滤波算法原理
对于振动信号,长度表示时间,高度表示幅值。因此,结构元素有必要从长度尺度和高度尺度这两方面来考虑。为此,定义了长度尺度λL和高度尺度λH,在对振动信号进行降噪处理时,形态学运算的结构元素由λL和λH共同确定。
2.1 基本原理
基于自适应结构元素广义形态滤波算法(Adaptive Structure Element for Generalized Morphology Filtering,简写为ASEGMF)的基本思路是[13]:
首先根据原始振动信号中相邻正峰值(或相邻负峰值)间隔的最小值和最大值自适应地确定λL;再根据信号峰值高度的最小值和最大值自适应地确定λH;利用小尺度的结构元素作为广义形态滤波的前级结构元素可以首先滤除信号中小尺度的噪声,再利用大尺度的结构元素作为广义形态滤波的后级结构元素滤除信号中大尺度的噪声,反之则会损失信号中有用的细节信号。这样采用一小一大的自适应结构元素来实现广义形态滤波处理,代入公式(7)~(9)就可以得到ASEGMF方法的计算结果。图1给出了具体图示。
2.2 具体构造过程
(1)选择合适的结构元素。
正弦形结构元素[14]的表达式为:
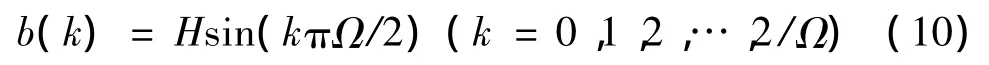
式中:H为正弦形结构元素的高度,k为正弦形结构元素的长度。由于在进行运算时正弦形结构元素取正弦波的半个周期波形,所以可得(kπΩ/2)∈[0,π]。
要处理的信号的形状决定了结构元素的形状设计,其结构要尽可能接近待分析的图形特点。汽轮发电机组的振动信号满足正弦或余弦函数的规律,因此在信号降噪处理中,选择正弦形的结构元素与待处理的信号形状最为接近。
(2)计算结构元素的长度尺度λL
通过计算原始振动信号X={xnn=0,1,2,… ,N-1}(N为振动信号的长度)的局部极大值和极小值,即对信号的局部峰值进行搜索。假设信号是经过零均值化预处理的信号,搜索的峰值包括信号的正峰值和负峰值。定义P={pnn=1,2,…,Mp}为搜索到的正峰值序列(pn>0),Mp为正峰值的数目;定义Q={qm|m=1,2,… ,Mq}为搜索到的负峰值序列(qm>0),Mq为负峰值的数目。
假设Mp>1和Mq>1,引入峰值间隔I的概念,即正峰值间隔为IP={in|in=pn+1-pn,n=1,2,…,Mp-1},负峰值间隔为IQ={im|im=qm+1-qm,m=1,2,… ,Mq-1}。
设自适应结构元素的长度尺度最小值和最大值分别为 λLmin和 λLmax,则:
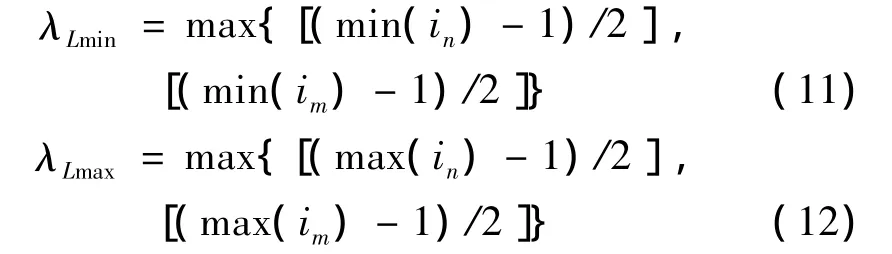
其中[·]为向上取整运算,[·]为向下取整运算。由式(11)计算得到的λLmin为广义形态滤波器的前级结构元素的长度尺度,而由式(12)计算得到的λLmax为广义形态滤波器的后级结构元素的长度尺度。
对于确定形状的结构元素,其长度应远小于待滤波函数,并大于干扰脉冲的宽度,这样才能去除脉冲干扰[15]。图1给出了含有尖峰脉冲干扰和随机噪声干扰的仿真信号局部放大的图形,根据上述正、负峰值和峰值间隔I的定义,在图1(b)中,以正峰值为例说明如何确定峰值间隔I。从图中可知,信号的正峰值为{p1,p2,p3,p4,p5,p6,p7,p8},峰值间隔为{i1,i2,i3,i4,i5,i6,i7},此时可根据峰值间隔确定结构元素的长度尺度。
(3)计算结构元素的高度尺度λH
为了充分利用信号局部峰值特征,使结构元素的高度尺度与长度尺度相匹配,引入峰值高度H,如图1(b)所示。峰值高度H定义为局部峰值点的高度减去其在原始振动信号中前一个采样步长的高度。
假设局部峰值在原始振动信号中的采样序列号为j,则其前一个采样步长为j-1,即正峰值高度HP=x(j)-x(j-1),负峰值高度HQ=|x(j)-x(j-1)|。
设自适应结构元素的高度尺度最小值和最大值分别为 λHmin和 λHmax,则:
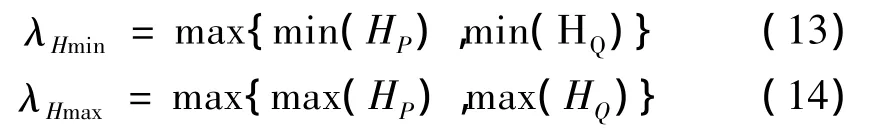
由式(13)计算得到的λHmin为广义形态滤波器的前级结构元素的高度尺度,而由式(14)计算得到的λHmax为广义形态滤波器的后级结构元素的高度尺度,这样就能保证小的长度尺度对应小的高度尺度,而大的长度尺度对应大的高度尺度。
在图1(b)中,峰值点p8的坐标为(j,x(j)),其高度为x(j),其前一个采样步长的坐标为((j-1),x(j-1)),其高度为x(j-1),则峰值点p8的峰值高度为HP=x(j)-x(j-1),其它峰值点的峰值高度也可以根据步骤(3)的定义相应求出,这样就能得到结构元素的高度尺度。
(4)计算自适应结构元素的广义形态滤波的结果。
由上面定义的长度尺度和高度尺度,可以自适应地得到广义形态滤波器的两级结构元素,而且该自适应的结构元素充分利用了原始振动信号的局部峰值的特征,更有利于抑制信号中的噪声干扰,将得到的一小一大自适应结构元素代入式(7)~(9)就可以得到ASEGMF方法的计算结果。
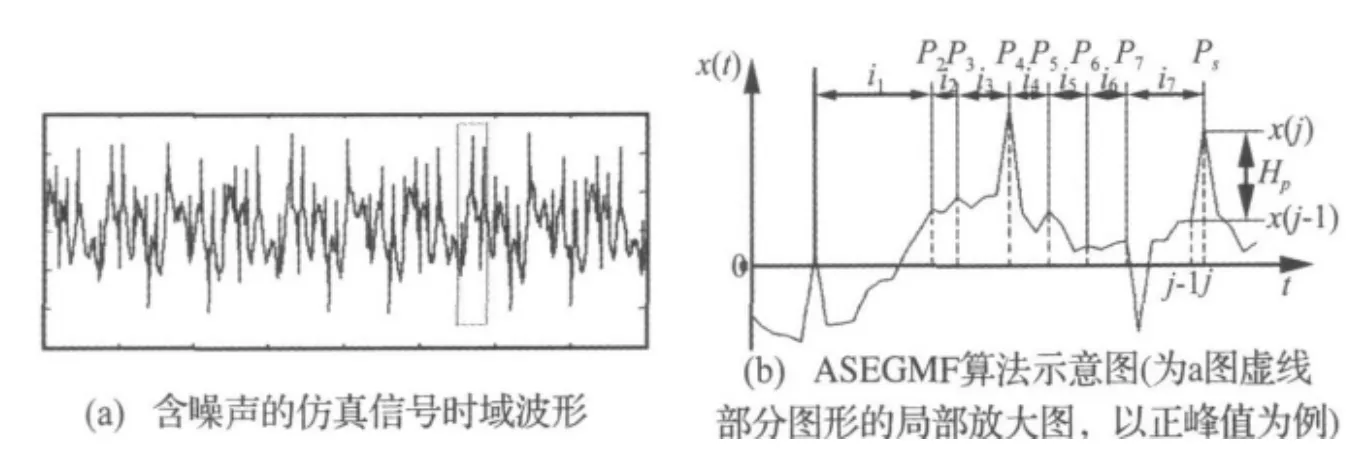
图1 含噪声的仿真信号时域波形及ASEGMF算法示意图Fig.1 Time waveform of interrupted signal and chart of ASEGMF algorithm
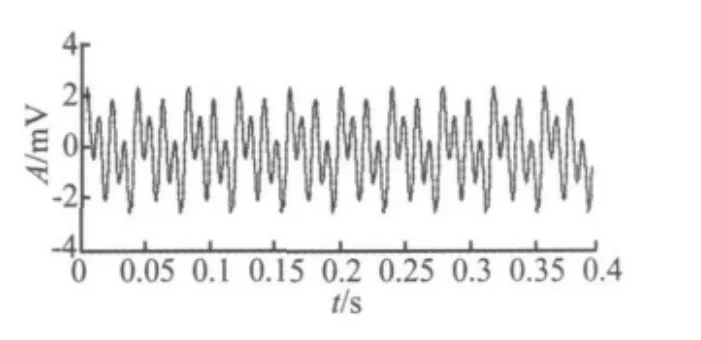
图2 仿真信号的时域波形Fig.2 Time waveform of simulated signal
3 ASEGMF的数值仿真试验
采用如下仿真方程来模拟汽轮发电机组发生不平衡、不对中和油膜涡动混合故障时转子的振动信号:
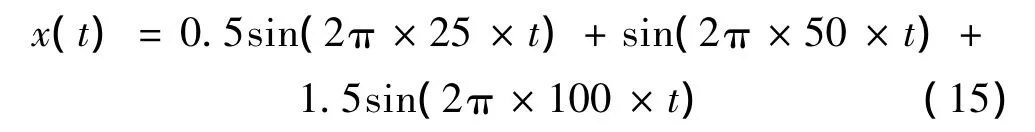
对信号进行整周期采样,取采样频率为2 kHz,图2给出了仿真信号的时域波形。
为考查ASEGMF方法的能力,在原始信号中加入周期尖峰脉冲干扰和不同标准差δ的白噪声构成的复合噪声i(t),使信号处于不同强度的噪声背景下。采用均方根误差[16]作为滤波效果的检验指标。对输入信号f(n),输出信号y(n),则有
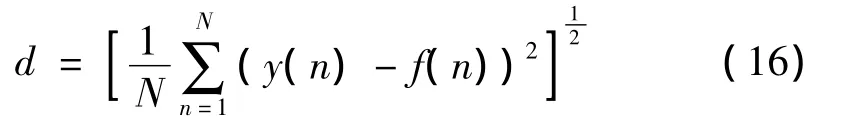
图3(a)给出了一个含噪声干扰信号的时域波形,在对信号进一步分析之前必须对原始信号进行降噪处理,以消除信号中所含的干扰噪声。

图3 含复合噪声的仿真信号时域波形及其降噪结果对比Fig.3 Time waveform of interrupted signal and de-noised results comparison
为与相同结构元素级联而成的形态滤波器进行比较,形态滤波器同样采用正弦形结构元素,表1给出了处于不同强度噪声背景下ASEGMF方法和形态滤波器对信号降噪效果的对比。
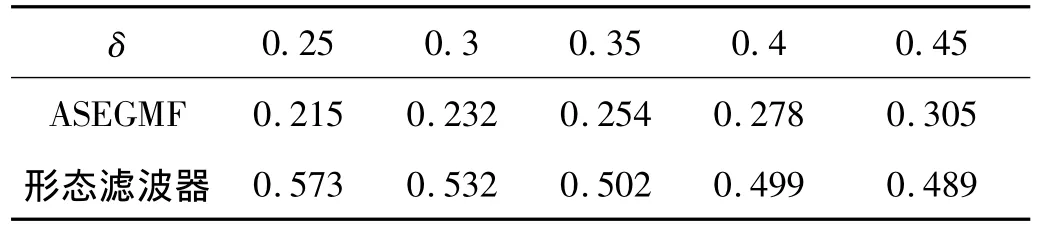
表1 不同强度噪声背景下降噪后的均方根误差对比Tab.1 Comparison of RMS error for de-noised signals under different noise background
由图3(b)、图3(c)和表1,可以得到以下几点启示:
(1)形态学运算中无需预知原信号的频谱特征,经过ASEGMF降噪处理后,信号中含有的周期尖峰脉冲干扰和白噪声干扰得到了很好的抑制,降噪后的时域波形基本保持了原始信号的波形特征。
(2)由于广义形态滤波器采用了一小一大的不同结构元素,其滤波降噪效果明显优于采用相同结构元素的形态滤波器。
(3)ASEGMF方法充分利用了信号的局部峰值特征,自适应得到的长度尺度和高度尺度避免了取值的随机性,消除了人为因素的影响,有利于提高降噪处理环节的自动化水平。
4 ASEGMF在实测信号降噪处理中的应用
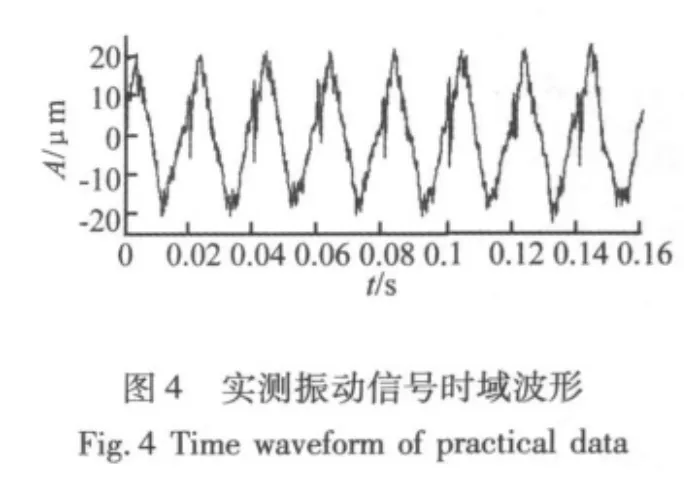
图4为某电厂实测汽轮机组振动信号,转速为3 000 r/min,采样频率为6 400 Hz。从图中可知,该振动信号由于受到尖峰脉冲和随机噪声的干扰而影响了振动特征的识别。
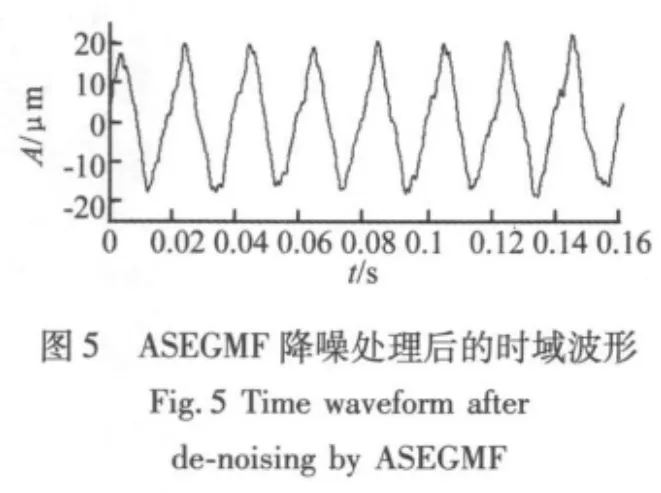
现采用ASEGMF方法对该信号进行降噪处理,以消除信号中的噪声干扰。图5为ASEGMF降噪处理后得到的信号时域波形。
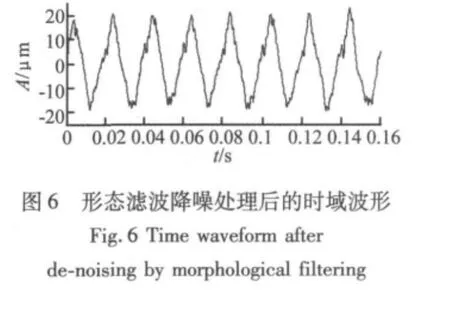
为便于对比,图6给出了形态滤波降噪处理后得到的信号时域波形。从图5、图6对比中可知,信号经过ASEGMF处理后,原信号中含有的尖峰脉冲干扰和随机噪声都得到了很好的抑制,这证明了本文提出方法的可行性和有效性。
5 结论
(1)提出了基于自适应结构元素的广义形态滤波算法。根据信号的局部峰值特征,定义了结构元素的长度尺度和高度尺度,并给出ASEGMF方法的构造过程。该方法克服了结构元素选择的随机性,能根据信号的特征自适应地选择合适的结构元素。
(2)采用正弦形结构元素对仿真信号和实测振动信号进行了降噪处理,原信号中含有的尖峰脉冲干扰和随机噪声都得到了很好的抑制,这证明了本文提出方法的可行性和有效性。
(3)形态学运算中无需预知原信号的频谱特征,通过简单的加减和极大、极小运算即可消除信号中的噪声干扰,算法简单且执行高效,非常适合旋转机械故障的在线监测和诊断。
[1]陈 果.一种转子故障信号的小波降噪新方法[J].振动工程学报,2007,20(3):285-290.
[2]吕志民,张武军,徐金梧.基于奇异谱的降噪方法及其在故障诊断技术中的应用[J].机械工程学报,1999,35(3):85-88.
[3]沈 路,周晓军,张文斌,等.广义数学形态滤波器的旋转机械振动信号降噪[J].振动与冲击,2009,28(9):70-73.
[4]崔 屹.图像处理与分析:数学形态学方法及应用[M].北京:科学出版社,2000.
[5]胡爱军,唐贵基,安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报,2006,42(4):127-130.
[6]张文斌,周晓军,林 勇.广义形态滤波器在振动信号处理中的应用研究[J].农业工程学报,2008,24(6):203-205.
[7]唐贵基,王维珍,胡爱军,等.数学形态学在旋转机械振动信号处理中的应用[J].汽轮机技术,2005,47(4):271-272.
[8]Maragos P,Schafer R W.Morphological filters.PartⅠ:Their set theoretic analysis and relation to linear shift invariant filters[J].IEEE Transactions on ASSP,1987,35(8):1153-1169.
[9]Maragos P,Schafer R W.Morphological filters.PartⅡ:Their relation to median,order-statistic,and stack filters[J].IEEE Transactions on ASSP,1987,35(8):1170-1184.
[10]王 楠,律方成,刘云鹏,等.自适应广义形态滤波方法在介损在线监测数据处理中的应用研究[J].中国电机工程学报,2004,24(2):161-165.
[11]赵春晖,李一兵,惠俊英.一种适于图像噪声平滑的广义形态滤波器[J].哈尔滨工程大学学报,2000,21(2):55-59.
[12]张兆礼,赵春晖,梅小舟.现代图像处理技术及Matlab实现[M].北京:人民邮电出版社,2001.
[13]张文斌.汽轮发电机组状态趋势预测及故障诊断方法研究[D].杭州:浙江大学,2009.
[14]荣太平,夏玉洁.形态滤波算法在油井测量数据处理中的应用[J].华中理工大学学报,2000,28(5):55-57.
[15]胡爱军,唐贵基,安连锁.振动信号采集中剔除脉冲的新方法[J].振动与冲击,2006,25(1):126-127.
[16] Serra J.Morphological filtering:An overview [J].Signal Processing,1994,38(4):3-11.

