声学数值计算的分区光滑径向点插值无网格法

姚凌云， 于德介， 臧献国

（湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082）

近年来，噪声预测和控制技术在车辆、飞机、潜艇等工程领域中得到越来越广泛的应用。声学数值计算是实现噪声控制和预测的关键技术，是进行结构噪声预测和优化设计的基础。针对Helmholtz声学方程的数值计算方法研究是近年来声学研究的一个热点，其研究重点在于如何提高声学数值计算的精度、计算效率、正确性以及算法的适用性。声学数值方法主要有有限元法（Finite element method，FEM）［1-5］、边界元法［6，7］和无网格（Meshfree）技术［8-10］等。

运用FEM求解声波方程时通常会遇到“数值色散”问题，即存在数值波的相位误差，数值仿真结果在高波数时色散严重。为了获得精度可靠的仿真结果，通常需要更精细单元和更高阶的多项式近似函数，这样势必增加计算时间和存储空间。为了降低色散效应，Petersen等［11］将高阶谱单元形函数应用到内部声学分析中，提高其计算精度和效率；Harari等［12］在声学波动方程的基本Galerkin形式下采用稳定化有限元法（Stabilized finite element method）提高数值方法的稳定性。

近年来，无网格技术在声学波动方程计算中有很大的应用和发展。Bouillard等［9］将无单元迦辽金法应用到声学波动方程的计算中，其结果的色散误差明显小于FEM结果。由于无网格法存在节点积分的不稳定性，Chen 等［13］提出了光滑应变技术。Liu［14］等将应变光滑技术和径向点插值法相结合，提出了节点光滑径向点插值法（Node-based conforming radial point interpolation method，NS-RPIM）；将有限元法与无网格中分区应变光滑技术相结合提出光滑有限元法（Smoothed finite element method，SFEM）［15］。Cui［16］用 SFEM 划分光滑域的思想与径向点插值法相结合，提出分区光滑径向点插值法（Cell-based smoothed radial point interpolation method，CS-RPIM），该方法提供合适的模型刚度，能很好地解决力学计算问题。

在声学数值计算中，由于“数值色散”效应导致计算误差随着波数k的增加变大。针对此问题，本文将CS-RPIM推广到声学问题的数值计算中，推导了CSRPIM计算二维声学方程的公式，利用分区光滑梯度技术对声压梯度进行光滑处理，只需对光滑域边界进行积分，有效降低因数值色散而引起的计算误差。为验证CS-RPIM求解声学波动方程的有效性，本文分析了二维管道声腔和车内声腔模型两个算例，结果显示：CS-RPIM分析声学问题时比FEM具有更高的精度和更好的收敛性，数值色散误差更小，在较高波数下仍具有较高的精度。

1 二维声学Helmholtz方程

结构振动在理想流体介质中引起的小振幅简谐声波满足Helmholtz波动方程：

式中：▽为拉普拉斯算子；k=ω/c为波数，ω表示圆频率；c表示声速。

声压与简谐声波的振动速度关系：

内部声场的边界条件为：

式中：p为边界处声压；n为腔边界表面法线方向；An为声导纳系数。

2 声学分区光滑径向点插值法基本理论

2.1 径向点插值法

对声场域内任意场点x声压p（x）采用耦合多项式基的径向点插值进行插值，有：

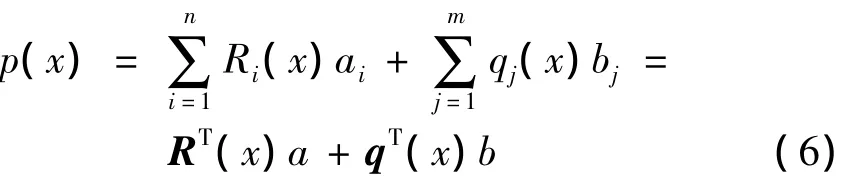
式中：Ri（x）是径向基函数，n是径向基函数的项数，qj（x）是多项式基函数，m是多项式基函数的项数，ai、bj为待定系数.。令近似声压向量p（x）为节点声压P，可得：

为求解系数ai和bj， 令：

联合方程式（7）和式（8）得：

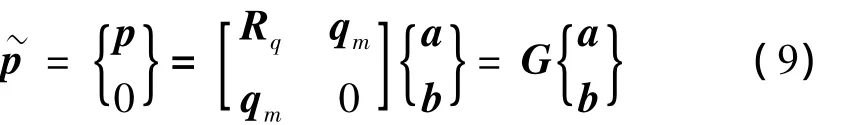
求解方程式（9）并将求解的未知量代入式（6）：

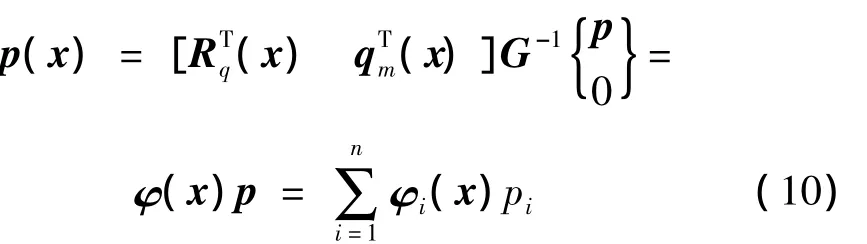
式中：φi（x）为节点形函数，pi为节点向量。

2.2 分区梯度光滑处理

分析二维声学问题时先将问题域Ω离散为容易生成的三角形背景单元，然后将三角形单元划分为若干个光滑区域（Smoothing cells，SC），满足 Ω1∪Ω2∪…ΩSC=Ω和Ω1∩Ω2∩…ΩSC=Ψ，其中Ψ表示空集；文献［16］中对背景单元光滑域的个数和形状进行了研究，研究光滑域的个数越多，积分就越硬，而一般有限元法全积分相当于光滑域为无穷多个，即SC=∞；当光滑域为1时，相当有限元法的缩减积分。在声学数值计算中光滑域的个数一般取3为宜。三角形背景单元划分光滑域个数1，3和4方式如图1所示。

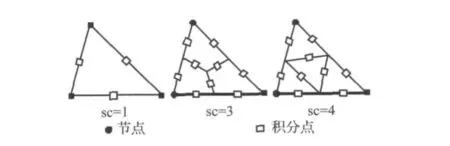
图1 背景单元划分光滑域示意图Fig.1 Division of background cell into SC smoothing cells

由式（7）可知声压梯度光滑处理的实质是速度光滑处理。在第C个光滑区域内，光滑速度表示为：

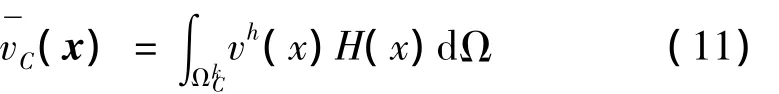
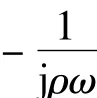
本文采用常值的光滑函数，如式（12）所示：

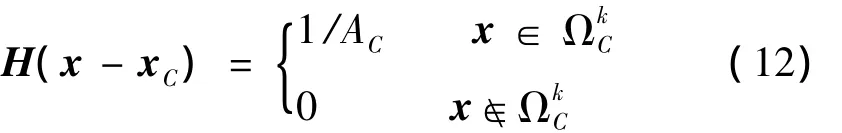
将式（12）代入式（11）并利用分步积分公式，在光滑域内的速度积分变为域边界上声压积分：

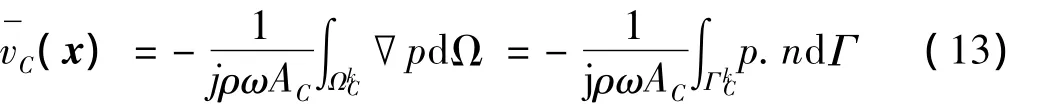
式中：为光滑域边界；n为光滑域边界法向单位矢量。将式（10）代入式（13），光滑速度写成：

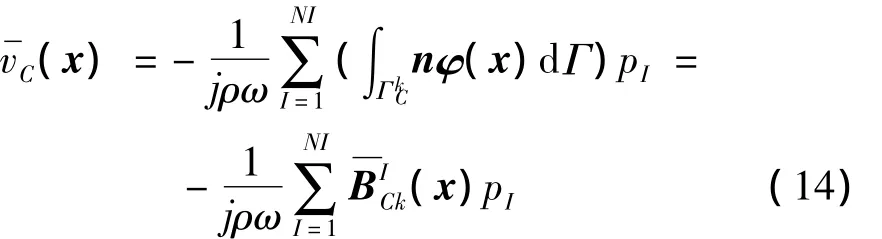
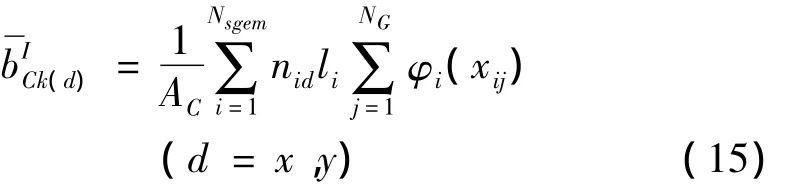
式中：N1为光滑域边界段个数；xij为第i边界段的第j个高斯积分点；nid为第i边界段的外法向矢量；li为第i边界段长度。

2.3 系统方程离散

CS-RPIM采用标准的Galerkin方法与声压梯度光滑处理相结合。在整个问题域里对Helmholtz方程及其边界条件进行离散处理，得到光滑的Galerkin弱形式：

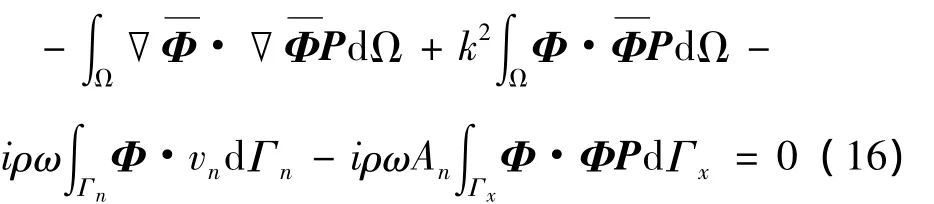
将式（10）和式（14）代入式（16）中，得到声域离散系统方程：

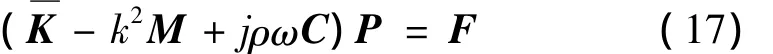
式中：Ncell为背景单元个数；Kij（k）为与单元Ωk相关联的刚度矩阵，表示为：

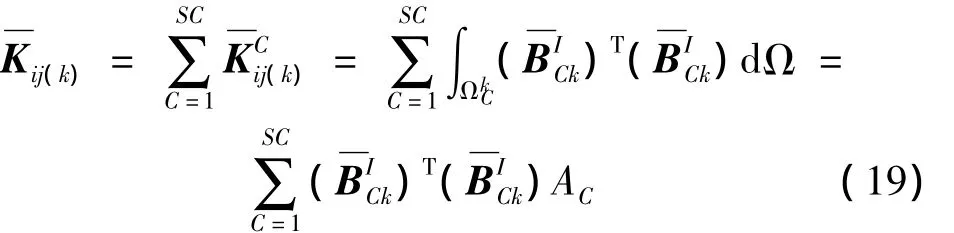
C表示由Robin边界条件得到的声学阻尼矩阵：

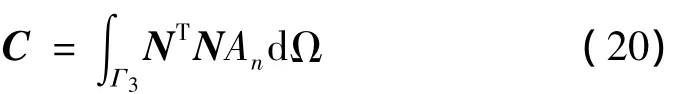
M表示声学质量矩阵，可以写成集中质量的形式：

F表示声压载荷矢量：

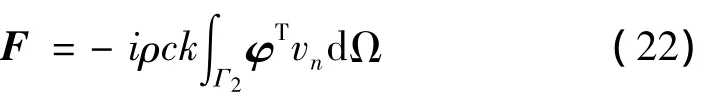
P表示节点声压矢量：

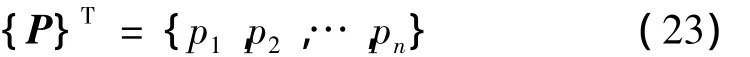
由上面的推导可以看出，应用梯度光滑处理可以使光滑声学梯度矩阵的计算简单，使区域的面积分变成边界线积分。

3 数值算例

3.1 管道声场分析

本节应用CS-RPIM分析文献［17，18］中算例模型，对一管道声场进行计算分析。调整管道声场参数：管长1 m、宽0.1 m；声场内部由空气流体填充，其密度ρ为1.225 kg/m3。声波在空气中的波速c=343 m/s，管子一端施加速度边界条件：法向速度vn=0.1 sin（ωt）；另外一端为刚性壁，如图2所示。

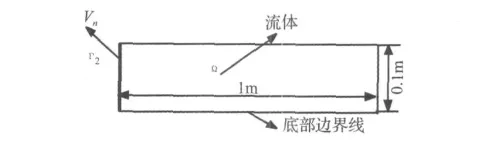
图2 管道声学模型Fig.2 The model of tube acoustic problem

管道声压的精确解为：

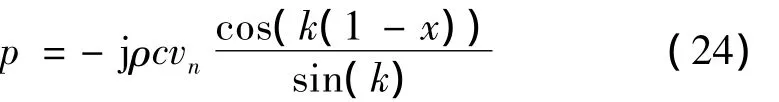
运用CS-RPIM分析背景单元尺寸为25 mm的不同频率（波数）下的声压分布。为了便于比较，应用FEM分析相同的网格模型。图3和图4分别表示管道中心线x方向的声压（虚部）分布。

为分析CS-RPIM结果的精度和收敛性，评价声学计算的相对误差：

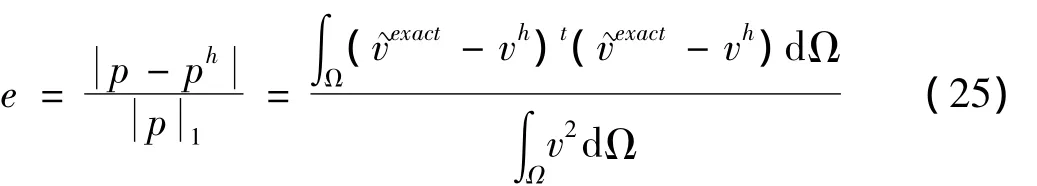
为分析声学网格的规则程度对CS-RPIM和FEM计算精度的影响，用不规则度参数来衡量网格的不规则程度。对于二维管道声域问题，对节点坐标进行如下变换：

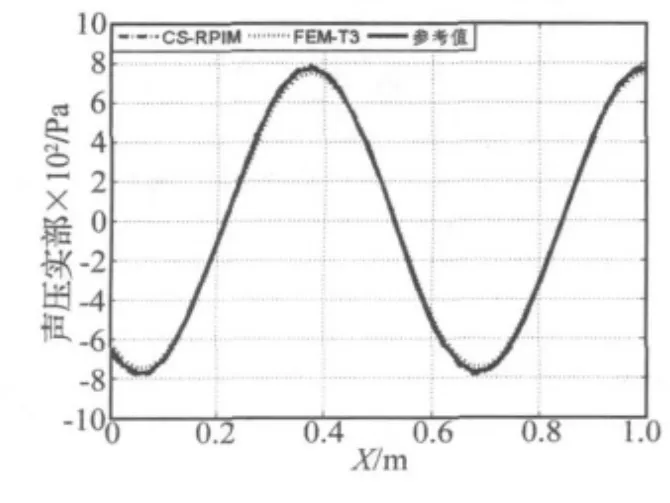
图3 波数为10的声压虚部分布Fig.3 Spatial distribution of real part of the pressure at k=10

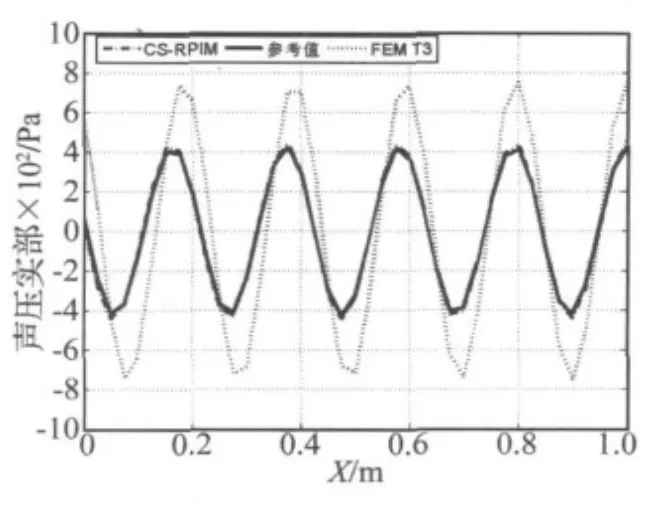
图4 波数为30的声压虚部分布Fig.4 Spatial distribution of real part of the pressure at k=30

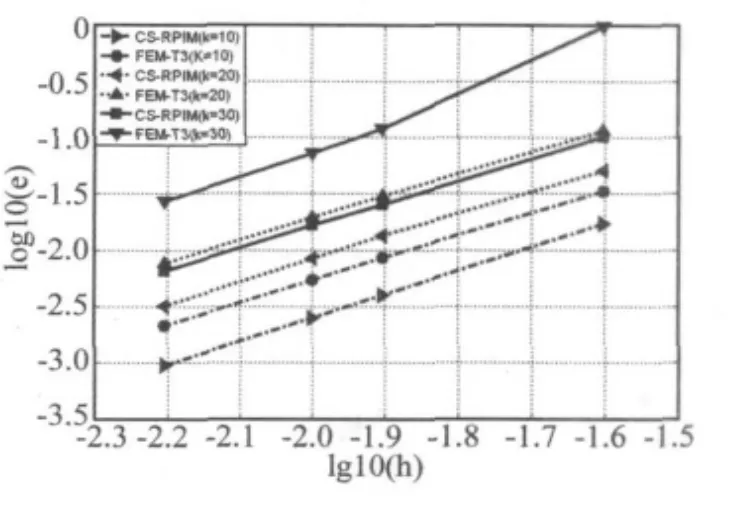
图5 CS-RPIM和FEM结果精度和收敛性的比较Fig.5 Comparison of accuracy and convergence property at different frequency values between CS-RPIM and FEM

式中：x'和y'为节点不规则变动后的坐标；x和y为原始坐标；Δx和Δy为初始规则单元节点之间的x和y方向的距离；rC是由计算机在（0.0，1.0）之间产生的随机数；βir为表示网格不规则度的参数，它在0.0和0.5之间。βir越大表明网格不规则程度越高。图6（a）、图6（b）分别表示βir为0和0.5时二维管道声场有限元网格。

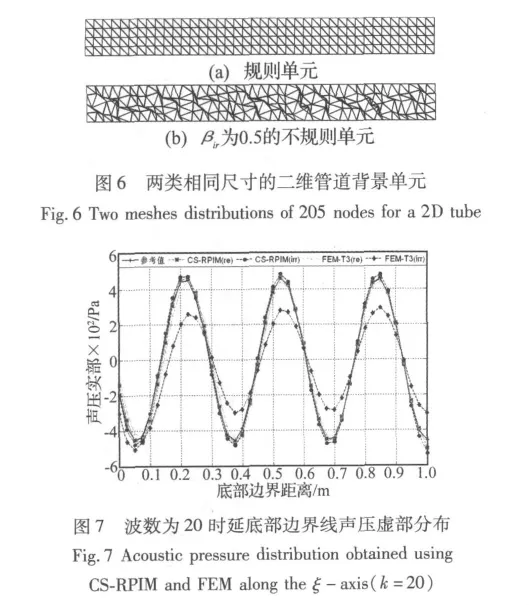
应用CS-RPIM对两种网格模型计算声压响应。图7为波数为20时管道声场底部边界线的声压分布。图中CS-RPIM（re）表示规则背景网格模型下应用CSRPIM的计算结果；CS-RPIM（irr）表示不规则背景网格模型下应用CS-RPIM的计算结果；FEM-T3（re）表示规则三角形网格模型下应用FEM计算结果；FEMT3（irr）表示不规则三角形网格模型的FEM结果。从图中可以发现，CS-RPIM对声学背景单元的网格不规则敏感度很低，在背景网格扭曲严重时仍然具有很高的精度。

3.2 轿车车内声场分析

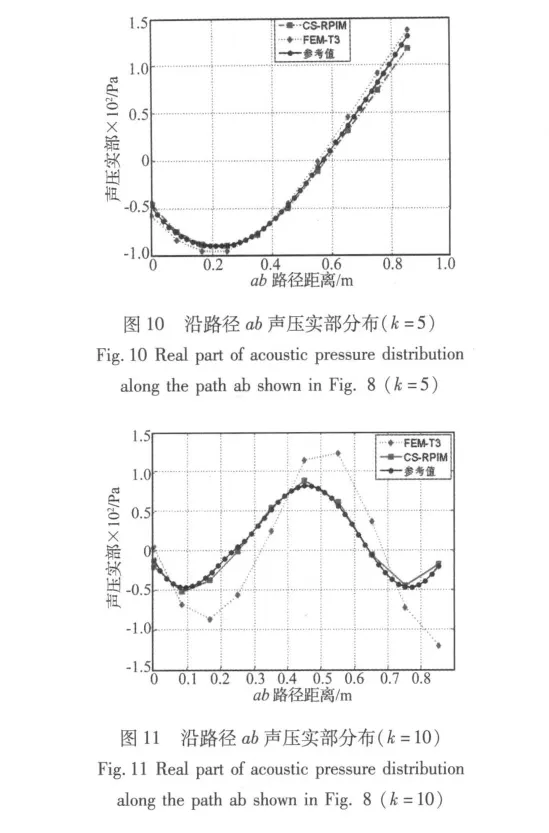
本节运用CS-RPIM分析轿车声腔模型。将车内声腔简化为二维模型，座椅简化为内部的一个空腔；边界条件为在声腔靠近发动机边界上法向振动速度vn=0.1 m/s，如图8所示。由HyperMesh自动生成三角形网格，单元数为347，节点数为219，如图9所示。空气密度为1.225 kg/m3；声速为343 m/s。

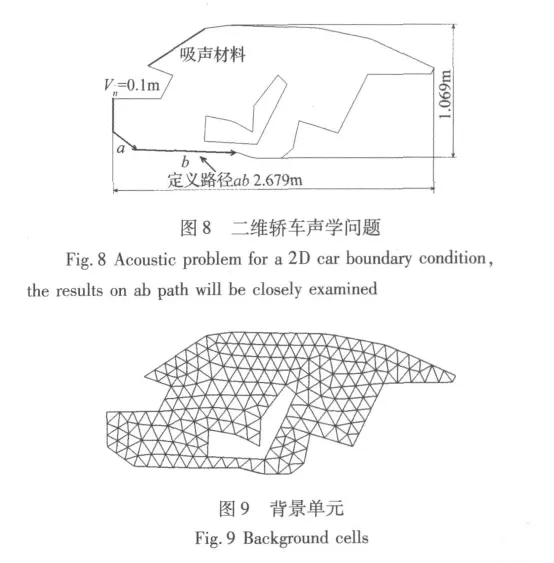
应用CS-RPIM和FEM分别对车内声腔网格进行计算，并对不同频率（波数）下的计算结果（声压虚部的分布）进行对比。图10和图11分别表示波速k=5和10时路径ab上的声压（虚部）分布。用FEM计算节点数为17 430的模型结果作为参考值。从图中可以发现，与FEM相比，运用CS-RPIM的计算结果精度随波数的增加变化不大，即CS-RPIM计算精度结果对波数k的灵敏度比FEM要小。

4 结论

本文推导了CS-RPIM求解声学波动方程的计算公式，将该方法应用到管道和车内声场的仿真分析中，研究结果表明：

（1）CS-RPIM在计算声学问题时能提供合适的模型硬度，有效降低因数值色散而引起的计算误差，因此其收敛性和结果精度比FEM更高。

（2）与FEM相比，CS-RPIM对计算波数（即频率）的敏感性较低，在较高波数时计算结果精度仍然很好。

（3）CS-RPIM对背景单元的质量要求很低，可以对扭曲严重的背景网格进行计算分析，因此可以在前处理分析中节省大量的人力和时间，具有良好的工程应用前景。

（4）由于CS-RPIM只是改进了声学刚度矩阵的计算，降低数值色散效应，因此CS-RPIM的计算结果受到计算频率、自由度和阶次的影响。

［1］朱才朝，秦大同，李润方.车身结构振动与车内噪声声场耦合分析与控制［J］.机械工程学报，2002，38（8）：54-58.

［2］ Bales L，Lasiecka I.Continuous finite elements in space and time for the nonhomogeneous wave equation［J］.Computers＆ Mathematics with Applications，1994，27 91-102.

［3］ Ihlenburg F，Babuška I.Finite element solution of the helmholtz equation with high wave number.Part 1：the hversion of the FEM［J］.Computers＆ Mathematics with Applications，1995，30：9-37.

［4］Richter G R.An explicit finite element method for the wave equation ［J］. AppliedNumericalMathematics，1994，16（1-2）：65-80.

［5］ Jenkins E W，Riviěre B，Wheeler M F.A priori error estimates for mixed finite element approximations of the acoustic wave equation［J］.SIAM Journal on Numerical Analysis，2002，40（5）：1698-1715.

［6］Chen J T，Chen K H，Chyuan S W.Numerical experiments for acoustic modes of a square cavity using the dual boundary element method［J］.Applied Acoustic，1999，57：293-325.

［7］程 昊，高 煌，张永斌，等.振动体声学灵敏度分析的边界元法［J］.机械工程学报，2008，44（7）：45-51.

［8］Wenterodt C，Estorff O V.Dispersion analysis of the meshfree radial point interpolation method for the Helmholtz equation［J］. InternationalJournalforNumericalMethods in Engineering，2009，77：1670-1689.

［9］Bouillard P，Suleau S.Element-free Garlekin solutions for Helmholtz problems：formulation and numerical assessment of the pollution effect［J］.Computer Methods in Applied Mechanicals and Engineering，1998，162：317-335.

［10］ Suleau S，Deraemaeker A，Bouillard P.Dispersion and pollution of meshless solution for the Helmholtz equation［J］.Computer Methods in Applied Mechanicals and Engineering，2000，190：639-657.

［11］ Petersen S，Dreyer D，Estorff O V.Assessment of finite and spectralelementshape functions or efficientiterative simulations of interior acoustics［J］.Computer Methods in Applied Mechanicals and Engineering， 2006， 195：6463-6478.

［12］ Harari I，Magoules F.Numerical investigations of stabilized finite element computations for acoustics［J］.Wave Motion，2004，39：339-349.

［13］ Chen J S，Wu CT，Yoon S，et al.A stabilized conforming nodal integration forGalerkin meshfree methods［J］.International Journal for Numerical Methods in Engineering，2001，50：435-466.

［14］ Liu G R，Li Y，Dai K Y，et al.A linearly conforming radial point interpolation method for solid mechanics problems［J］.International Journal of Computational Methods，2006，3（4）：401-428.

［15］ Liu G R，Nguyen T T，Dai K Y，et al.Theoretical aspects of thesmoothed finite elementmethod （SFEM）［J］.International Journal for Numerical Methods in Engineering，2007，71：902-930.

［16］ Cui X Y，Liu G R，Li G Y，et al.A cell-based smoothed radial point interpolation method（CS-RPIM）for static and free vibration of solids［J］.Engineering analysis with boundary elements，2010，34（2）：144-1570.

［17］ Bouillard P. Admissible fields and error estimation for acousticFEA with low wavenumbers.Computersand Structures，1999，73：227-237.

［18］ He Z C，Liu G R，Zhong Z H，et al.An edge-based smoothed finite elementmethod （ES-FEM）foranalyzingthreedimensional acoustic problems［J］.Computer Methods in Applied Mechanicals and Engineering，2009，199：20-33.