弹簧近似法在二维非结构动网格生成技术中的应用

霍世慧， 王富生， 岳珠峰

（西北工业大学 力学与土木建筑学院，西安 710129）

在工程实际问题中，存在着很多包括运动边界的非定常复杂流场，如自由液面流动问题、流体与结构耦合问题、气动弹性问题、强迫振动及多体分离问题等，这些问题中运动边界的处理是计算流体力学的一个难题。在这些问题的求解过程中，计算区域随着时间的变化而变化，相应区域网格也需发生改变。在网格的变形中，常用到的有网格重生成和网格变形技术。网格重生成技术是根据结构变形修改几何模型，并全部或部分重新生成模型网格；网格变形技术是基于原有网格进行网格位置、形状的修改生成新的网格，而网格的拓扑结构没有发生改变。网格重生产技术生成模型网格的过程复杂，耗费大量的时间，而且在模型局部特殊部位需要手动修改才能生成较好的网格，限制了动网格的应用，而网格变形技术只是对网格进行位置、形状的修改，很好地克服了网格重生成技术中的这些缺点。本文将开展网格变形技术在动网格中的应用研究。

目前国内外发展的可靠性较高的网格变形技术主要有弹性体近似法［1－3］（Elastic solid method，ESM）和弹簧近似法［4－8］（Spring analogy method，SAM）。弹性体近似法是把整个计算区域看成一个弹性体，通过求解控制网格点移动的基本方程来求出网格内部点的位移；弹簧近似法是把整个计算区域看成一个由弹簧组成的系统，当边界发生运动时，内部网格点按当地的运动强度重新布置达到新的平衡。

国内外已经开展了很多基于弹簧近似法的研究，Batina［4］提出了弹簧近似法在三角形非结构动网格中的应用，并将其应用到机翼颤振问题的分析研究中；Farhat［5］在弹簧近似法中引入了扭转系数，在一定程度上避免了网格边的交叉，扩大了弹簧近似法的应用范围；Blom［6］定义了弹簧近似法的两种描述方法及其倔强系数的选取，并研究了其在二维可动边界问题中的应用；Mitsuhiro［7］实现了弹簧近似法在三维动网格中的应用，并提出了根据单元形状对倔强系数的修正；Zhang［8］将弹簧近似法和局部网格重生成联合运用到动网格中，提高了网格的变形能力。上述文献分别从扭转系数、单元形状和局部网格重生成等几个方面对弹簧近似法进行了一定的改进，并将其应用到实际问题的研究中，得到了很多有用的结论，但都没有对变形后的网格质量进行系统的分析。本文将开展变形后网格质量的研究，并讨论将网格质量引入倔强系数后的网格变形能力。

1 弹簧近似法

弹簧近似法是将网格单元的各条棱边假设为弹簧，边界发生运动后，内部网格由弹簧控制达到新的平衡，从而生成变形后网格。弹簧近似方法有两种描述方法［6］：一种是将弹簧的平衡长度假设为零，称为顶点弹簧（Vertex springs）；另一种是将弹簧的平衡长度假设为其变形前长度，称为棱边弹簧（Segment springs）。顶点弹簧近似法能够用于网格变形和网格优化中，网格变形中认为网格节点的受力始终等于初始状态所受的合力；网格优化中则认为网格节点始终处于平衡状态。本文主要研究顶点弹簧近似法在网格变形中的应用。

在顶点弹簧近似法中，节点i，j间的弹簧张力可以表示为式（1）：

其中：Kij为连接节点i，j弹簧的倔强系数；ri、rj分别为节点i，j的位置矢量。假设计算区域中共有N个节点与节点i相连，则其合力可表示为：

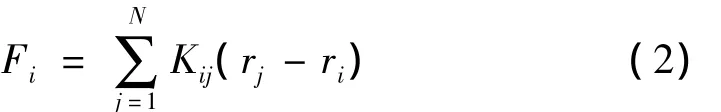
由式（2）可得整个计算区域中m个节点在初始状态下的矩阵表达式为：

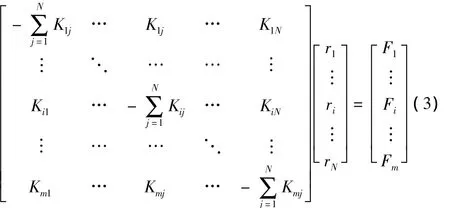
当模型边界发生变形时，通过改变模型边界的位置矢量和增加适当的外边界限制条件，如计算区域外边界位置矢量保持不变、模型边界位置矢量改为新位置下的矢量等，运用Gauss－seidel迭代法对式（3）进行迭代求解，其相应的分量迭代格式可表示式为：

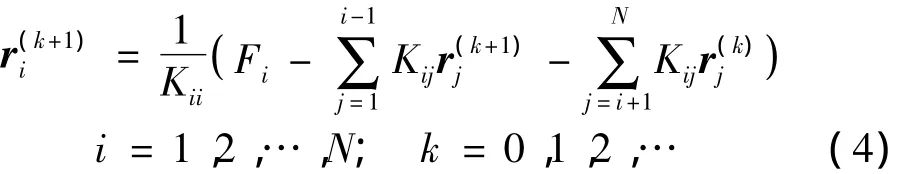
当模型发生变形时，利用式（4）对式（3）进行数次迭代，达到所需要的精度时，便可得到计算区域中各网格节点变形后坐标。

2 弹簧倔强系数的选取

在上述弹簧近似法的描述中，各单元棱边都被假设为一弹簧，都具有各自的倔强系数K，下面将进行弹簧倔强系数选取的研究。

2.1 传统方法

在传统弹簧倔强系数的选取中一般都只把网格边的边长作为参考值来定义［6］。弹簧倔强系数选取的一般格式为：

式中：lij为网格边的边长，当lij→0时，Kij→∞，这样较好地避免了网格节点i与j发生相撞，使网格取得较好的疏密特征，但在处理一些边界发生较大运动或变形问题时，容易产生体积为负的无效单元。近年来，许多文献中也提出了对传统弹簧倔强系数的改进方法。史爱明［9］在传统弹簧倔强系数中引入了对单元几何尺寸的控制，每个时间步更新弹簧倔强系数，从而保证体积最小单元不会成为体积为负的无效单元，取得了较好的效果，其具体表达式为：

其中，Vmin为拥有网格边ij单元的最小体积。Farhat［5］在每个网格的顶点上加了一个扭转弹簧，每一个连接在顶点i的三角形单元扭转弹簧的扭转刚度Ci如式（7）所示：

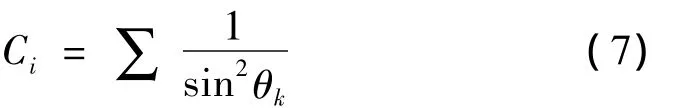
其中，θk为以i为顶点三角形面单元的内角。当边界发生运动或变形时，对每个顶点均可得到关于拉伸弹簧的力平衡方程和扭转弹簧的力矩平衡方程，联立求解得出计算区域内的新网格点。

2.2 方法改进

网格的质量随着边界运动或变形发生变化，下面将开展网格质量的研究并提出相应的改进方案。图1给出了在二维顶点弹簧近似法中，三角网格模型容易产生的狭长、扁平两种典型畸形网格单元。

单元的这两种畸形情况严重影响着网格整体质量，并最终导致网格边的交叉。为了使动网格达到最大限度的变形情况、推迟畸形网格的出现，就必须在弹簧倔强系数中引入对网格质量的控制。对网格质量的评定，主要有倾斜度和纵横比两个指标［10］，其计算公式分别为：

图1 典型畸形网格单元Fig.1 Classical abnormal meshes

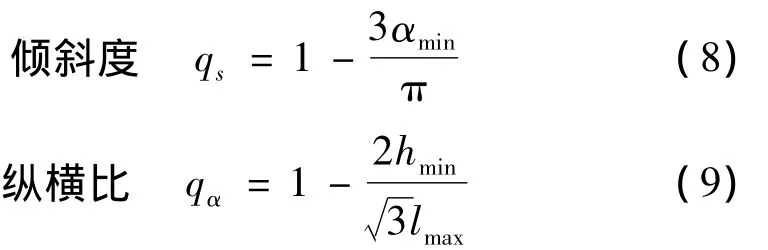
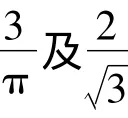
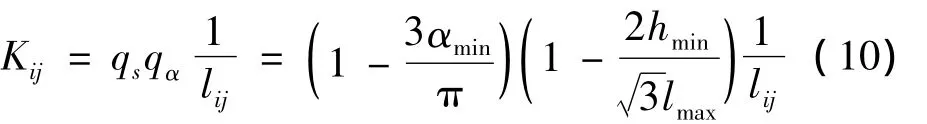
在网格的变形过程中，通过两个网格质量评定指标的修正，逐渐增大网格质量较差单元各棱边的倔强系数，使网格质量较好单元承担一定的变形。

3 方法应用

在进行弹簧近似法的应用之前，首先引入两种评定网格变形指标［11］：单元面积变化和单元形状变化。通过这些指标来量化网格的变形，分析网格的变形程度。其具体评价方式为：

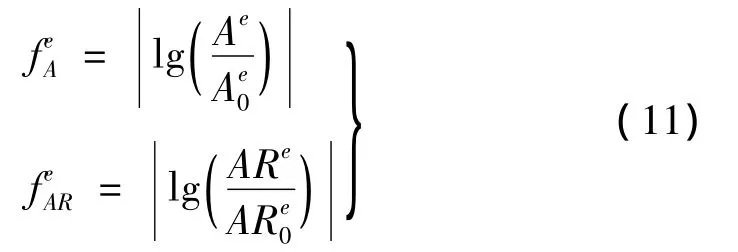
本文在算例一中采用NACA23012翼型，对其计算区域采用非结构化离散，图2（a）为翼型初始二维气动网格，该网格是由非结构三角形单元组成，共计有67 160个节点、133 966个单元，图2（b）为翼型表面网格局部图。

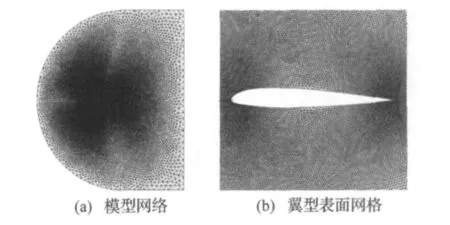
图2 NACA23012初始气动网格Fig.2 Original mesh of NACA23012

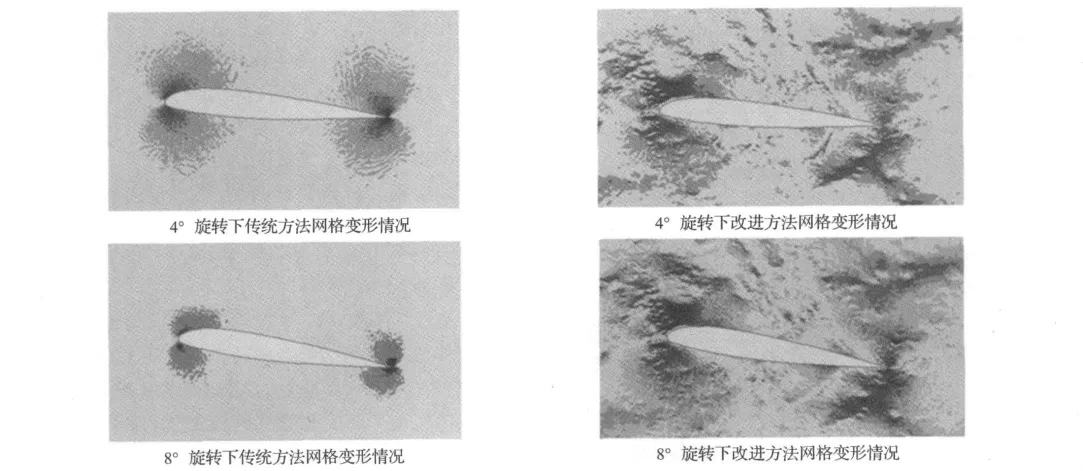
图3 网格变形指标变化情况Fig.3 The change of mesh deformation value

机翼的变形表现在二维翼型中为翼型的旋转，下面将针对NACA23012翼型通过软件Fortran编写传统和改进的弹簧近似法程序生成其不同旋转角度时网格。为了清楚地比较两程序生成网格中各单元的变形情况，图3给出了在发生相同旋转角度时，两方法生成翼型周围各网格的变形指标值。图3中区域颜色的深浅直接表示该处网格变形指标值的大小，随着颜色的加深值增大，区域网格变形加剧。

从图3可以明显地看到，传统弹簧近似法在翼型前缘和后缘处网格变形指标较大，而其它区域网格变形指标较小，网格的变形主要集中在翼型前后缘处；改进弹簧近似法生成网格的变形指标呈现以前缘、后缘点为中心向外扩展的形式，网格的变形较为分散，缓解了翼型前后缘的变形压力。

图4给出了传统和改进弹簧近似法下，计算区域网格整体变形指标fA、fAR随翼型旋转角度的变化情况。

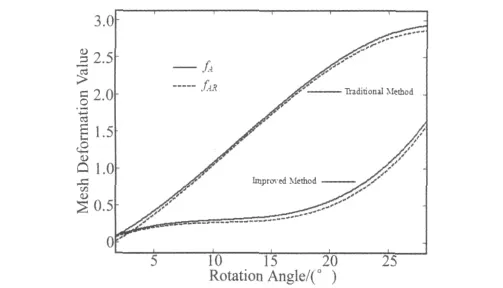
图4 变形指标随旋转角度变化曲线Fig.4 Deformation value with the increase of rotation angle

从图4可以发现，随着翼型旋转角度的增加，fA、fAR均逐渐增大，网格变形随旋转角度的增加而增大。比较图4中相同旋转角度两种弹簧近似法生成网格的变形指标可以发现，改进的弹簧近似法fA、fAR值始终低于传统方法，改进的弹簧近似法将边界的变形压力分散到了整个计算区域，降低了整体网格的变形指标值。

改进的弹簧近似法缓解了网格变形在计算区域局部集中出现的情况，将变形压力分散到整个计算区域，下面将开展变形压力分散前后，两种方法生成网格的质量变化情况的研究。图5给出了翼型边界发生旋转时两种弹簧近似法生成网格的整体网格质量变化曲线。

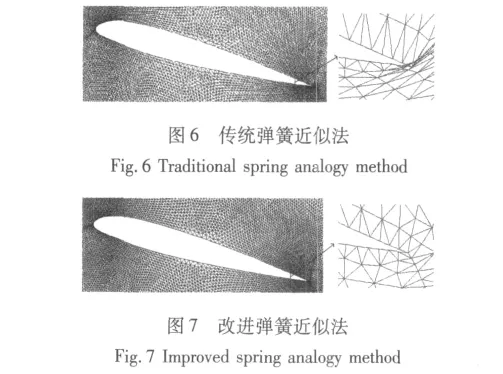
从图5中可以看出：传统和改进的弹簧近似法生成网格的qs、qa均随旋转角度的增加而增大，网格质量下降；发生相同旋转角度时，改进的弹簧近似法生成的网格质量均优于传统弹簧近似法；传统方法在边界发生13°旋转角度时，qs、qa值达到1，网格质量最差，无法继续使用，改进方法在边界发生27°旋转角度时qs、qa值才达到1，通过方法的改进，提高了网格的变形能力。图6、图7分别给出了翼型发生14°旋转时运用两种弹簧近似法生成的网格局部图，右边小图为翼型后缘局部网格放大图。

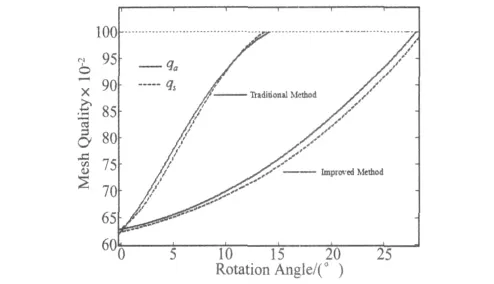
图5 网格质量随旋转角度变化曲线Fig.5 Mesh quality with the increase of rotation angle

对比图6、图7中两种弹簧近似法生成的翼型发生14°旋转时网格，可以很明显地看出，传统弹簧近似法在后缘局部发生了网格边的交叉，网格不能继续使用，而改进弹簧近似法网格却能够保持较好的质量。

4 算例

4.1 算例一

运用改进的弹簧近似法生成非结构动网格，分析二维NACA23012翼型不同攻角下的升力系数变化情况NACA23012翼型初始网格如图2所示，图8给出了运用改进弹簧近似法生成的翼型在 －5°、0°、5°和10°攻角下网格局部图。

运用上面生成的翼型网格，选定雷诺数为6.0×106，分析了机翼在不同攻角下的升力系数。图9给出了机翼升力系数随攻角的变化情况，并与参考文献［12］所得到的实验数据进行比较。

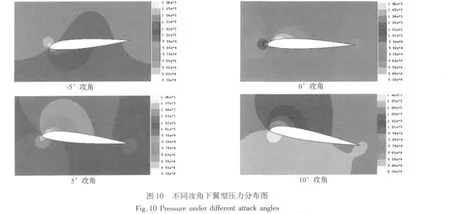
观察图9中曲线可以发现：雷诺数为6.0×106时，NACA23012翼型升力系数随攻角的增大而提高，在攻角达到12°左右时，翼型发生失速，升力系数开始下降。通过将模拟结果与实验数据比较发现，该模拟方法能够较好地得出翼型的升力系数变化情况。图10给出了翼型在 －5°、0°、5°和 10°攻角下翼型周围压力分布情况。

图8 翼型周围网格局部图Fig.8 Close-up views of mesh around airfoil

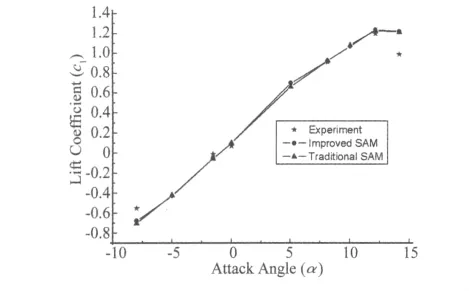
图9 升力系数随攻角变化情况Fig.9 Effect of Attack Angle on Lift Coefficient

4.2 算例二

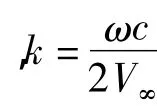
比较图11、图12可以发现，翼型升力系数的变化趋势与翼型攻角的变化完全吻合，其周期均为T=2π/ω=51.1 s，这与实际情况较为吻合。图13给出了升力系数与翼型攻角的变化曲线，并与传统弹簧近似法及实验数据进行比较。

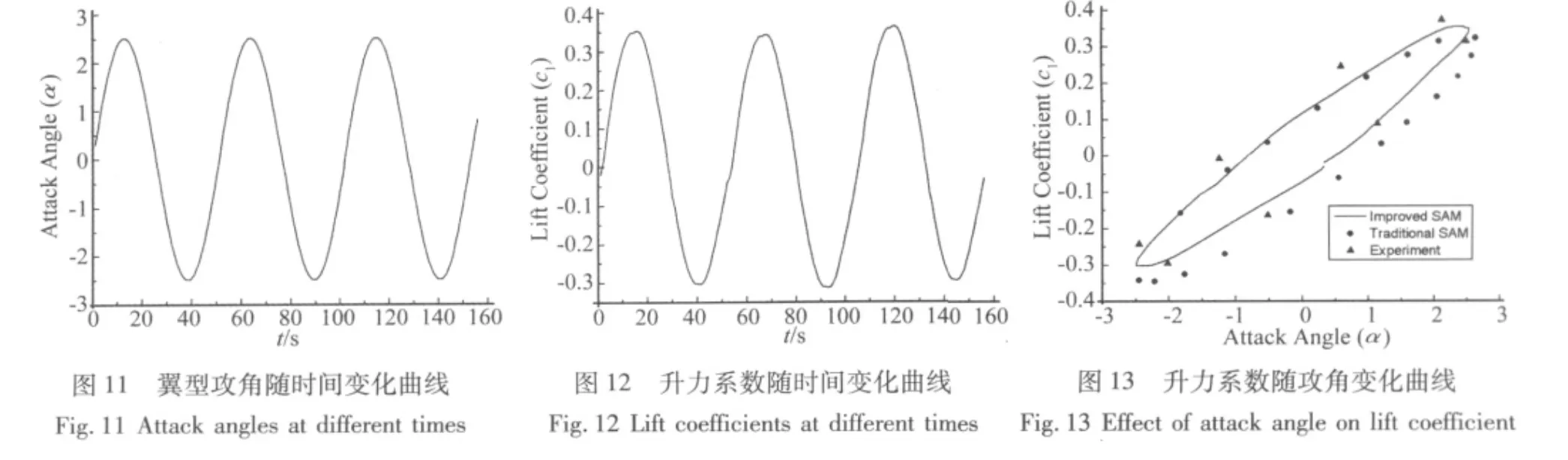
由图13可以发现，改进弹簧近似法生成的动网格在二维谐和振动翼型非定常气动力的求解中能够得到较传统方法更接近于实验数据的结果，该方法能够较好地运用于实际的数值模拟中。

5 结论

通过本文分析可以得到以下结论：

（1）随着模型边界旋转角度的增大，网格质量逐渐下降；边界旋转角度增大到一定程度时，在翼尖周围网格出现严重变形甚至发生网格边交叉现象。

（2）通过引入网格质量改进弹簧近似法，改进的弹簧近似法在网格整体质量、局部畸形情况上都较传统方法有所改善。

（3）在边界发生旋转时，传统弹簧近似法生成网格变形主要集中在翼型前后缘处，容易发生局部网格变形集中；改进的弹簧近似法将变形分散到了整个计算区域，缓解了局部网格的变形压力。

（4）在模型发生较大旋转角度时，传统弹簧近似法无法生成可用的网格，而通过对倔强系数的修正使最大旋转角度有了较大的提高。

（5）运用改进的弹簧近似法对二维翼型进行数值模拟，并与实验数据进行比较，得到了较满意的结果，该方法能够较好地运用于实际数值模拟中。

［1］ Rausch R D，Batina J.Spatial adaptation procedures on tetrahedral meshes for unsteady aerodynamic flow calculations［J］.AIAA Paper 93－0670，AIAA 31stAerospace Sciences Meeting.1993.

［2］ Baker T，Vassberg J.Tetrahedral mesh generation and optimization［J］.Proc.6thInternational Conference on Numerical Grid Generation，ISGG，1998：337－349.

［3］Baker T J，Cavallo P A.Dynamic adaptation for deforming tetrahedral meshes［J］.AIAA Paper，A99 － 3253，1999：19－29.

［4］Batina J T.Unsteady euler airfoil solutions using unstructured dynamic meshes［J］.AIAA Paper，AIAA 27thAerospace SciencesMeeting， Reno， Nevada， 1990，28（8）：1381－1388.

［5］Farhat C，Degand C，Koobus B，et al.An improved method of spring analogy for dynamic unstructured fluid meshes［J］.AIAA Paper，98 －2070.

［6］ Blom T J.Considerations on the spring analogy［J］.Journal of Aircraft，2000，32：647 －668.

［7］ Mitsuhiro Murayama，et al.Unstructured dynamic mesh for large movement and deformation［J］.AIAA 2002 －0122.

［8］ Zhang S J，Liu J，Chen Y S.A dynamic mesh method for unstructured flow solvers［J］.AIAA Computational Fluid Dynamics Conference，2003－3843.

［9］史爱明.非结构动网格下的非定常气动力计算和嗡鸣研究［D］.西安：西北工业大学，2003.

［10］ Software M S C.MSC.patran user’s manual［M］.Los Angeles：The Macneal－ Schwendler Corporation，2005.

［11］ Singh K P，Newman J C，Baysal O.Dynamic unstructured method for flows past multiple objects in relative motion［J］.AIAA Journal，1995，33（4）：641 －649.

［12］ Abbott I H，Von Doenhoff A F.Theory of wing sections，including a summary of airfoil data［M］.New York：Dover Publications，1959.

［13］ Bohn D E，Moritz N.Algebraic method for efficient adaption of structured grids to fluctuating geometries［J］.Proceedings of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，2005，219（4）：303 －314.

［14］ Ivan M.Dynamic finite element meshes for 3D lagrangian CFD［J］.AIAA Paper，AIAA 16thComputational Fluid Dynamics Conference，Orlando，Florida，June 2003.

［15］ Charbel Farhat，Ajaykumar Rajasekharan and Bruno Koobus.A dynamic variational multiscale method for large eddy simulations on unstructured meshes［J］.Comput.Methods Appl.Mech.Engrg，2006，195：1667 －1691.

［16］ Fernando de Goes，Siome Goldenstein，Luiz Velho.A simple and flexible framework to adapt dynamic meshes［J］.Computers ＆ Graphics，2008，32：141 －148.