覆冰输电线路舞动气动阻尼识别

王 昕， 楼文娟， 沈国辉

（浙江大学 结构工程研究所，杭州 310058）

输电导线舞动是指因覆冰改变其圆形断面，造成气动力特性的变化，形成气动失稳，所表现出的大幅低频振动，属于典型的驰振现象。导线舞动的直接因素是气动力所代表的阻尼项是负阻尼，即负气动阻尼的存在是舞动的必要条件，对其进行识别有助于验证舞动机理、深入研究舞动影响因素，进一步增加对舞动的认识。覆冰导线在风力作用下气动阻尼产生的机理十分复杂，它不仅同导线覆冰截面、风场特征、风速和风攻角等相关，还受到导线的振动形式和振幅的影响。

目前，对于高层建筑和大跨屋盖风振响应的气动阻尼问题已有一定数量的研究［1－4］，此类问题中气动阻尼通常为正值，对结构风振响应起抑制作用。有学者对导线覆冰后准静态气动力参数以及受迫运动下的动态气动力参数进行了试验研究［5－8］，但在覆冰线路自激舞动过程中针对响应进行的气动阻尼识别则鲜有涉及。

本文在风洞中模拟了两种断面形式的覆冰输电线路气弹模型的舞动现象，记录了其竖向和扭转运动响应，并利用Hilbert变换进行了气动阻尼的识别，研究了不同风速、风攻角和线路动力特性下覆冰线路气动阻尼的幅值及变化规律，以及覆冰断面和导线数量、布置形式对气动阻尼的影响，并对D形覆冰导线纯竖向舞动气动阻尼比与根据Den－Hartog机理计算所得理论值进行了比较。

1 覆冰线路舞动气弹模型

试验于大连理工大学风洞试验室（DUT－1）进行，风洞试验段长18 m，横断面宽3 m，高2.5 m。覆冰导线刚性节段模型通过吊臂、弹簧和支架相连，模型固定于吊臂中心，两侧吊臂各通过上下弹簧悬挂于支架上，通过弹簧和配重模拟线路的竖向和扭转运动动力特性，在风洞中构建了竖向－扭转二自由度覆冰输电线路气弹模型。试验导线覆冰截面分为D形和新月形2类，如图1所示。为调整模型竖向/扭转自振频率比，弹簧悬挂点与吊臂中心的距离可自由调节，同时在吊臂两侧安放的配重质量及其距吊臂中心的位置同样可调。

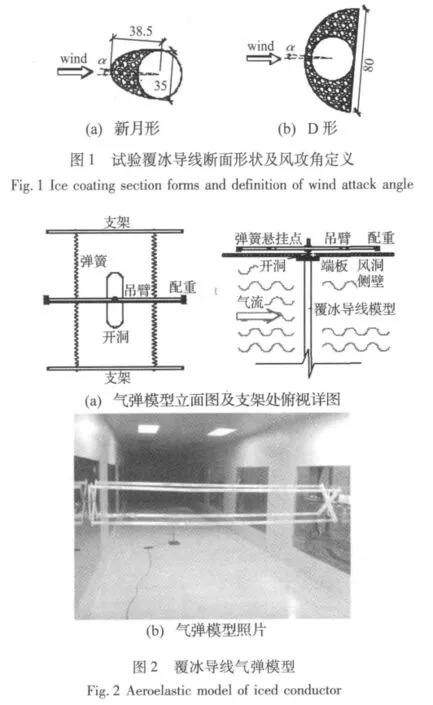
为避免覆冰导线模型以外的装置对风洞中流场造成干扰，吊臂、弹簧和支架等均放置于风洞外侧，模型通过风洞两侧洞口与吊臂相连，洞口高400 mm、宽120 mm，通过预紧弹簧和调整配重质量，使模型在洞口处的初始位置位于洞口中心。气弹模型示意图及照片如图2所示。

试验所用导线节段模型包括D形覆冰单根导线、新月形覆冰单根导线、新月形覆冰二分裂导线和四分裂导线。对于分裂导线，先按照初始位置将其固定于端板，再将端板和吊臂连接（见图2（b）），使各分裂导线同步运动并绕分裂导线中心转动。分裂导线间距均为400 mm，各子导线在覆冰偏心扭矩下初始向下偏转15°，布置形式及风攻角定义如图3所示。试验中对于每种导线模型，进一步通过弹簧悬挂点位置和配重的调节，将其分为竖向/扭转自振频率接近（fy≈fθ）和扭转频率明显高于竖向频率（fy≪fθ）两种工况。对于每一种工况，不断调整风攻角α直至模型失稳产生明显的大幅度舞动现象（新月形覆冰单根导线未能产生明显舞动），改变风速，通过加速度传感仪记录其加速度响应时程，并进一步转换为位移和转角响应。试验各工况系统参数和动力特性见表1。

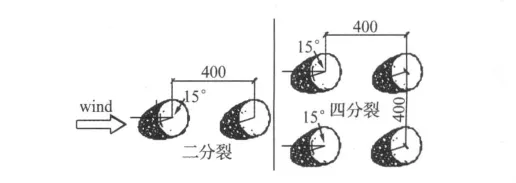
图3 分裂导线初始位置布置示意图Fig.3 Initial position of bundled conductors

表1 气弹模型系统参数和动力特性Tab.1 Parameters and dynamic characteristics of aeroelastic model

2 气动阻尼识别方法

目前气动阻尼的识别方法主要是通过气弹模型风洞试验获得结构响应的时间历程，然后采用频域方法或时域方法来识别气动阻尼［9］。频域方法可分为对数递减法、谱距法、谱曲线拟合法、半功率带宽法等；时域法则可分为自相关衰减法、最大熵法、随机减量法及系统识别法等。

对于高层建筑和大跨屋盖风振响应的气动阻尼识别由于其响应数据通常来源于环境激励下，同时此类结构具有多阶模态参与响应，因此目前通常先采用经验模态分解法（Empirical mode decomposition，EMD），对响应信号中各阶模态响应进行提取，并对其应用随机减量法（Random decrement technique，RDT），通过多次平均化处理使得响应中的强迫振动响应分量趋向于零，从而对信号进行自由衰减响应的提取，最后运用Hilbert变换对其各阶模态气动阻尼进行识别。

而对于输电线路舞动的气动阻尼识别，由于舞动响应主要来源于风激励中的平均分量，其表现为低频率、大振幅，环境激励（即风激力中的脉动分量）对其影响极为有限。同时本文将输电线路动力模型简化为仅具有竖向和扭转两项自由度的线性化气弹模型，其舞动响应方式仅有纯竖向和扭转竖向耦合两种单一模态，因而导线舞动响应信号仅来源于单一模态响应，可直接对其进行Hilbert变化，进而得到Hilbert谱。对一给定响应信号C（t），其Hilbert变换定义为：

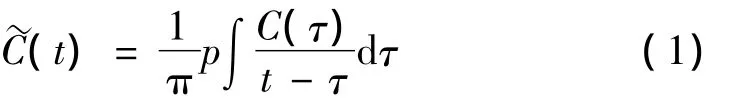
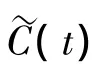
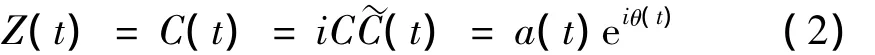
对舞动响应信号进行Hilbert变换后，可得到其瞬时振幅和瞬时频率，它们都是时间的函数，能很好的反映信号的瞬时特性。

单自由度线性振动系统的位移响应可表示为：

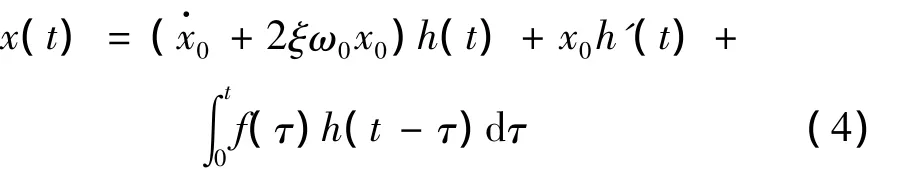
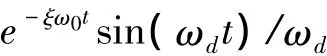
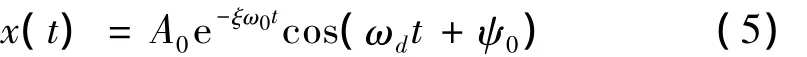
与x（t）对应的解析信号z（t）为：

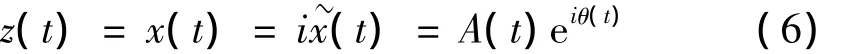
其中，A（t）与θ（t）可以表示为：

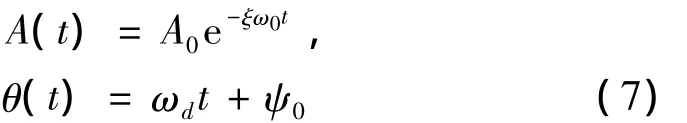
对幅值和相位分别引入对数及微分算子，可得：

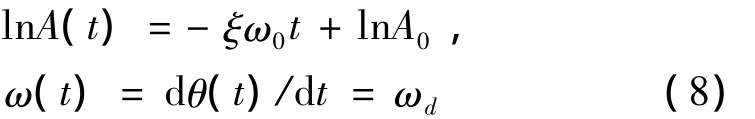
可见，系统阻尼和频率等动力特性参数即可通过上述关系识别。

3 Den Hartog舞动理论的气动阻尼

试验中导线模型将产生纯竖向舞动和竖向－扭转耦合舞动两类舞动形式，当纯竖向舞动时，根据Den-Hartog机理，可得其舞动起始阶段以对数衰减关系表示的竖向气动阻尼比的理论表达式为［10］：

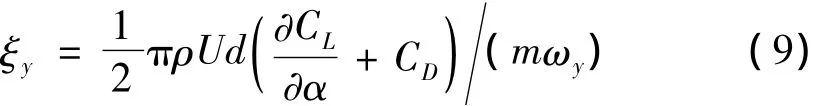
式中，ρ为空气密度，U为来流风速，d为导线模型断面迎风宽度，m为模型单位长度质量，ωy为模型竖向自振频率，（∂CL/∂α+CD）则为根据覆冰导线截面升力系数和阻力系数所得Den-Hartog系数，从式（9）中可以看出，当Den-Hartog系数＜0时，系统气动阻尼比为负，从而引发导线失稳舞动。对于竖向－扭转耦合舞动，由于两个自由度之间的耦合效应，机理较为复杂，难以给出某单一自由度气动阻尼比的显式表达式。

以往舞动研究中对Den Hartog机理的验证往往仅限于舞动稳定性的判定，本文以D形覆冰单导线模型为例，在大连理工大学DUT－1风洞内用测力天平得到了模型气动三分力系数，如图4所示。根据式（9）计算出模型竖向舞动时理论气动阻尼比，并与根据实测响应所识别的气动阻尼比进行了比较，从而于气动力系数试验值和气弹模型响应试验值两方面对Den Hartog机理进行了更为深入的验证。

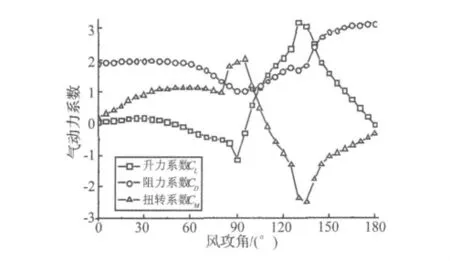
图4 D形覆冰单导线气动力系数Fig.4 Aerodynamic coefficient of single D section iced conductor

4 由舞动响应识别的气动阻尼

4.1 舞动类型及响应识别范围

风洞中覆冰输电线路气弹模型舞动将产生两类典型的竖向响应时程，如图5所示。图5（a）产生于导线纯竖向舞动（fy≪fθ）或竖扭耦合舞动（fy≈fθ）但扭转响应较小时，此时竖向舞动响应由于气动负阻尼作用不断吸收能量而逐渐增大，直至能量平衡响应达到稳定状态；而图5（b）则发生于竖扭耦合舞动（fy≈fθ）且扭转舞动响应较大时，竖向响应在增大过程中将与扭转响应进行能量交换，使得扭转响应增大，竖向响应减小后进入平稳过程。扭转舞动响应则通常如图5（c）所示，逐渐增大至稳定状态。

另外可见，导线舞动响应在增大过程中，其增长速率可能为非线性，并且由于竖向运动速度的变化导致来流相对风攻角也不断变化，因而不同于理论气动阻尼比，导线舞动实测气动阻尼比相当于对导线舞动起始后一定时间内不断变化的气动阻尼进行了平均化处理。

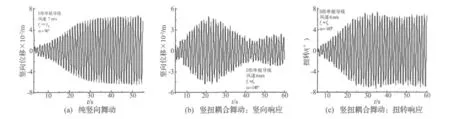
图5 舞动竖向和扭转响应Fig.5 Vertical and rotational responses of galloping

为了使不同工况及不同风速下气动阻尼存在可比性，对于气动阻尼识别的舞动响应信号截取范围作了以下规定，对竖向和扭转响应的识别时间分别取自舞动初始状态至各自响应达到最大时刻。对图5（a）所示竖向舞动响应增长段信号进行Hilbert变换，得到其振幅的对数值lnα与相位角θ的原始曲线如图6所示。再对lnα与θ进行线性拟合后（抛弃两端，截取曲线中部平滑段进行拟合），即可识别出系统舞动阻尼比，减去用同样方法根据模型自由振动响应衰减曲线所识别出的系统固有阻尼比之后（如表2所示），即为系统舞动时的气动阻尼比。

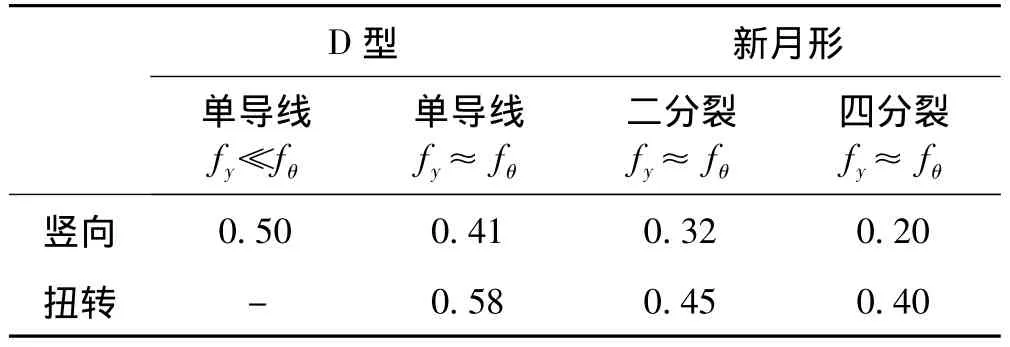
表2 气弹模型固有阻尼比（10－2）Tab.2 Critical damping of aeroelastic model（10－2）

4.2 D形单导线舞动气动阻尼

D形单根导线在2个风攻角下各自2类竖向/扭转自振频率比下产生舞动，其气动阻尼比如图7和图8所示，其中当fy≪fθ时，扭转响应极小可忽略，仅识别竖向响应的气动阻尼比，并与理论值进行比较；而当fy≈fθ时，则同时识别竖向和扭转响应信号的气动阻尼比。

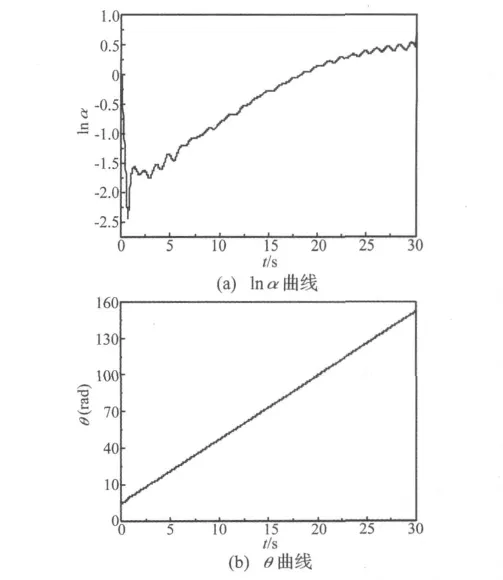
图6 竖向舞动响应的lnα与θ曲线Fig.6 Curve of lnα and θ from vertical galloping response

可见，在试验风速范围内，竖向和扭转舞动气动阻尼绝对值均随着风速增大而增大。当fy≪fθ，即气弹模型只产生竖向舞动响应时，145°风攻角下气动阻尼比绝对值随风速的增长速率略大于90°风攻角，两者数值较为接近。同时，两个风攻角下的理论气动阻尼比绝对值均略大于实测值，这是由于导线自舞动起始阶段至稳定阶段其气动负阻尼不断衰减，使得其平均值小于起始阶段的理论值。

当fy≈fθ时，2个风攻角下气弹模型均表现出竖扭增大；90°风攻角下气动负阻尼绝对值则有所减小，随风速的增长速率则基本保持不变。另一方面，对于舞动扭转气动负阻尼绝对值而言，145°风攻角对应绝对值明显大于90°风攻角。可见覆冰线路舞动时扭转响应对竖向响应气动阻尼的影响机理较为复杂。转耦合的舞动形式，有所区别的是，90°风攻角下扭转响应较小，竖向响应类型如图5（a）所示；145°风攻角下则扭转响应较大，竖向响应类型如图5（b）。此时，对于竖向响应而言，145°风攻角下气动负阻尼绝对值相比纯竖向舞动时显著增大，其随风速的增长速率同样

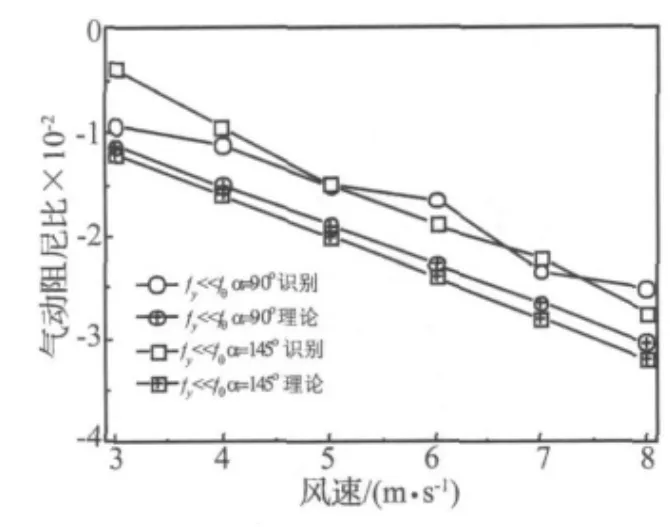
图7 D形单根导线纯竖向舞动气动阻尼比Fig.7 Critical aerodynamic damping of single D section iced conductor vertical galloping

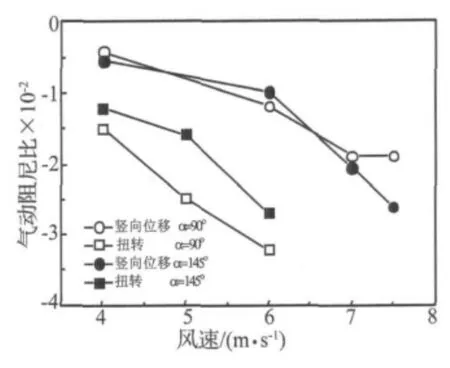
图8 D形单根导线竖扭耦合舞动气动阻尼比Fig.8 Critical aerodynamic damping of single D section iced conductor vertical-torsional coupled galloping

图9 新月形分裂导线竖扭耦合舞动气动阻尼比Fig.9 Critical aerodynamic damping of bundled Crescent section iced conductors vertical-torsional coupled galloping

4.3 新月形分裂导线舞动气动阻尼

在本次试验过程中，单根新月形覆冰导线在两种不同竖向/扭转频率比下均未能在风洞中观测到舞动现象。而新月形分裂导线则能够产生舞动现象。

新月形二分裂导线在fy≈fθ，风攻角为180°时产生竖向－扭转耦合舞动，新月形四分裂导线则在fy≈fθ，风攻角为－8°时同样发生竖向－扭转耦合舞动，两者舞动气动阻尼如图9所示。另外fy≪fθ时，两者则均不发生舞动。可见，新月形单根导线缺乏能够引起气弹模型失稳舞动的气动负阻尼，同样覆冰断面的分裂导线则能够产生舞动，扭转响应对于舞动的激发起重要作用，而分裂导线数量和布置形式的区别则导致了起舞风攻角区别，并且其相应的气动阻尼也有较大区别，新月形四分裂导线竖向和扭转气动负阻尼的绝对值均超过二分裂导线，两者随风速的增长速率则较为一致。

5 结论

本文制作了D形和新月形覆冰输电线路的气弹模型，通过调整竖向/扭转频率比和风攻角，在风洞中记录了其发生舞动时竖向和扭转响应，运用Hilbert变换对其气动阻尼进行识别。主要结论如下：

（1）竖向和扭转舞动气动阻尼比均为负值，在试验风速范围内，其绝对值均随风速增大而增大。

（2）单根D形覆冰导线在90°和145°风攻角下纯竖向舞动的气动阻尼比较为接近，同时其绝对值均略小于理论气动阻尼比；而竖向扭转耦合舞动时，90°和145°攻角下扭转气动阻尼比相差较大，并且扭转响应对竖向气动阻尼比的影响有所不同。

（3）单根新月形覆冰导线未出现舞动现象，新月形覆冰二分裂和四分裂导线均出现竖向扭转耦合舞动现象，但二分裂和四分裂导线气动阻尼比存在一定差异，说明同样覆冰断面形状的分裂导线因子导线数量的区别气动阻尼有所区别。

［1］楼文娟，孙炳楠.风与结构的耦合作用及风振响应分析［J］.工程力学，2000，17（5）：16－22.

［2］ Marukawa H，Kato N，Fuji K，et al.Experimental evaluation of aerodynamic damping of tall buildings［J］.Journal of Wind Engineering＆ Industrial Aerodynamics，1996，59：177－190.

［3］楼文娟，卢 旦，杨 毅，等.开孔建筑屋盖风振响应中的气动阻尼识别［J］.空气动力学学报，2007，25（4）：419－424.

［4］潘 峰，孙炳楠，楼文娟.基于Hilbert-Huang变换的大跨屋盖气动阻尼识别［J］.浙江大学学报（工学版），2007，41（1）：65－70.

［5］Renaud K，Jean-Louis L.Benchmark cases for galloping with results obtained from wind tunnel facilities-validation of a finite element model［J］. IEEE Transactions on Power Delivery，2000，15（1）：367－374.

［6］Stumpf P，H C M N G.Investigation of aerodynamic stability for selected inclined cables and conductor cables［D］.Winnipeg，Canada，University of Manitoba，1990.

［7］Chadha J，Jaster W.Ifluence of turbulence on the galloping instability of iced conductors［J］.IEEE Transactions on Power Apparatus and Systems，1975，94（5）：1489－1499.

［8］李万平.覆冰导线群的动态气动力特性［J］.空气动力学学报，2000，18（4）：413－420.

［9］ Kareem A，Gurley K.Damping in structure：its evaluation and treatment of uncertainly［J］.Journal of Wind Engineering＆ Industrial Aerodynamics，1996，59：131－157.

［10］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京：中国电力出版社，2002.