压电夹层梁的分岔、混沌及主动控制

张 鹏， 贾中印

(河北建材职业技术学院 信息机电系，秦皇岛 066004)

柔性结构的振动主动控制研究已成为当前动力学领域的前沿课题，压电材料由于具有良好的机电耦合性能，广泛应用于结构主动控制系统中。压电梁结构简单，且有着广泛的工程背景，人们对这种结构的动力稳定性、振动控制、分岔与混沌等问题进行了许多研究。

Sun 和 Huang［1，2]讨论了压电复合结构的控制问题，建立了含有压电层的三阶剪切变形层合梁模型，并给出了近似解。Chen等人［3]对轴向力作用下压电复合梁的动力稳定性和反馈控制进行了分析。Gao和Shen［4]采用增量有限元方法分析了粘贴有压电作动层的层合板的几何非线性瞬态振动，并应用负速度自反馈控制策略进行主动控制。Moita等人［5]对几何非线性压电复合结构进行了分析。董兴建和孟光［6]基于一阶剪切变形理论，在压电悬臂梁应变最大处配置致动器和传感器，实现了低阶系统的主动控制。Akl［7]将可变形机翼简化为层合梁，建立了非线性有限元控制方程。李凤明、孙家春等人［8]研究了参数激励压电梁的动力稳定性，分析了轴向力、电压、非线性阻尼等因素对稳定性的影响。傅衣铭、阮建力［9]基于高阶剪切变形理论，采用耦合正、逆压电效应的负速度反馈控制原理，分析了具损伤压电智能层合板的非线性主动控制和损伤监测。Belouettar等人［10]研究了压电夹层梁非线性振动的主动控制，讨论了夹层梁大幅振动和小幅振动对反馈控制的影响。近些时候，姚志刚、张伟等［11]研究了压电复合材料层合梁的分岔和混沌动力学响应，并分析了压电激励控制混沌的可行性。高美娟、张伟［12]等基于三阶剪切变形理论，采用能量相位法和数值模拟对压电复合材料层合板的混沌动力学进行研究。

本文研究了轴向激励作用下简支压电夹层梁的混沌动力学响应，采用工程当中易于实现的比例微分反馈控制方法将夹层梁整体组成一个闭环控制系统，结果表明，通过调节比例控制增益和微分控制增益都可以抑制系统通过倍周期分岔进入混沌运动，把系统控制到不同的稳定极限环上，保持系统运动的稳定性与可控性，且该方法简单有效。

1 反馈控制策略

考虑图1所示矩形截面细长夹层梁，它由上下两层压电材料和中间弹性层构成。上表面为压电传感层，下表面为压电作动层，它们之间通过一控制器相联系。该夹层梁长度为L，其它几何尺寸如图所示。其边界为左端简支滑动且受轴向力作用，右端简支不可移动。

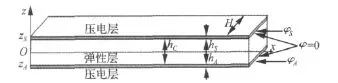
图1 压电夹层梁模型Fig.1 The model of piezoelectric-elasticpiezoelectric sandwich beam

根据 Euler-Bernoulli梁理论，梁的位移场假设如下:

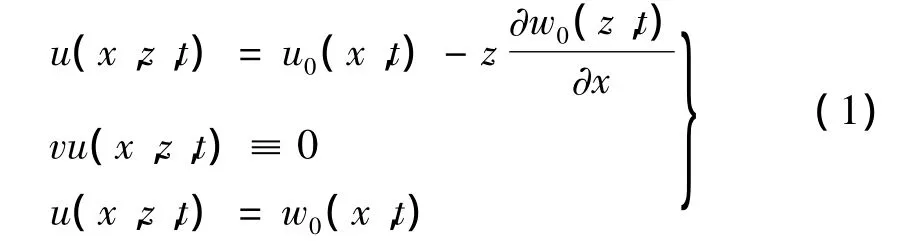
式中，u(x，z，t)、w(x，z，t)分别为沿 x 和 z方向梁内任一时刻的位移。

对应式(1)的von Karman几何非线性应变位移关系为:

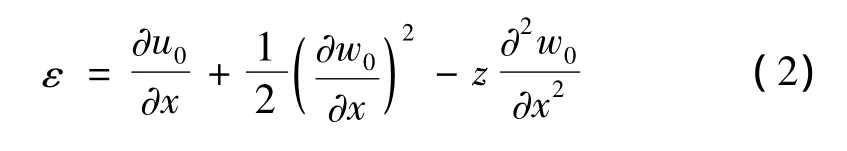
上下两层压电材料的本构关系为:

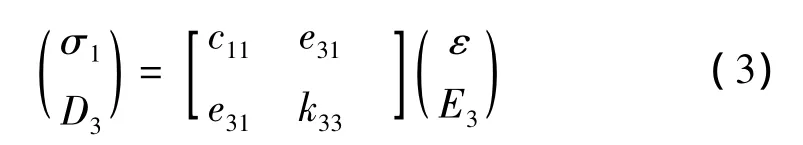
式中，σ1、D3、E3分别为 x方向的应力和 z方向的电位移和电场强度，c11、e31和k33分别为压电材料的弹性常数、压电常数和介电常数。

假定弹性层和压电层完全粘结，不发生任何滑动，根据静电平衡方程有自由体电荷密度=0，结合电位移边界条件可得:

将式(4)代入式(3)中，结合式(2)可得到压电层电场强度和位移的关系:

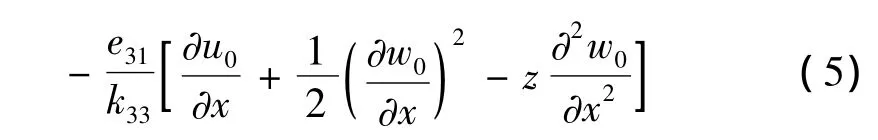
根据电场强度和电势之间的关系E3=，压电层上下表面电势差可写为:

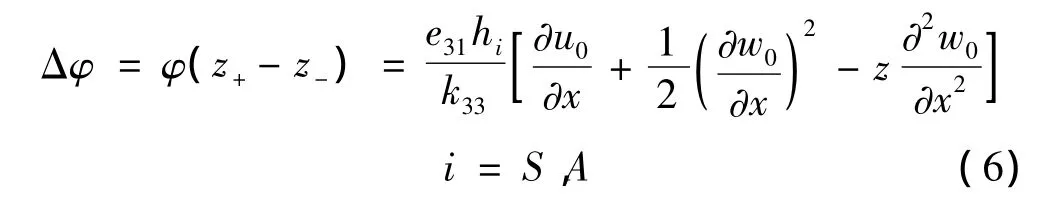
其中:φ表示电势，下标S表示压电传感层，A表示压电作动层。将式(6)代入式(5)中得到:

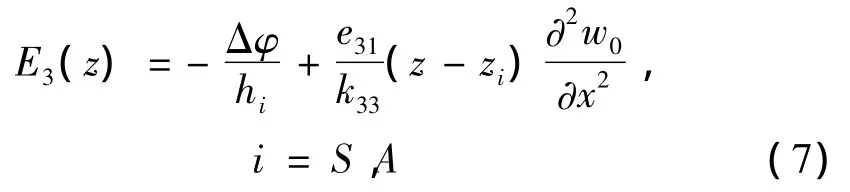
考虑到夹层梁的中间弹性层为一等势体，不失一般性，假设其电势为0，则夹层梁上表面的电势为:

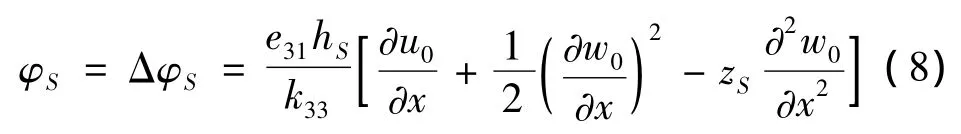
为了实现对夹层梁振动的主动控制，必须将传感层和作动层组成一个整体以形成一个闭环控制系统，本文采用以下控制策略:

其中Gp表示电势比例增益，Gd表示电势微分增益。

联立式(7)～式(9)可以得到传感层和作动层的电场强度:

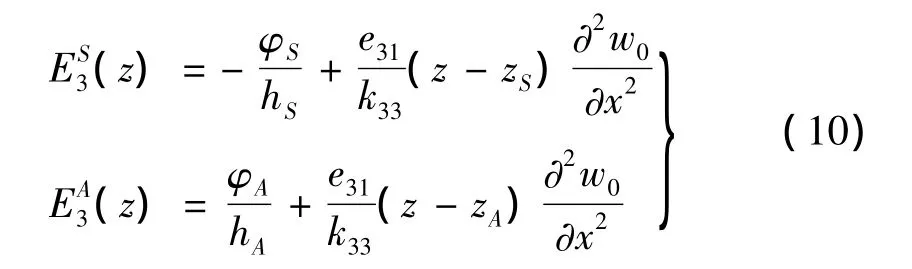
上式中 zS=(hC+hS)/2，zA=(hC+hA)/2。

2 动力学方程的建立

Hamilton原理可以表示为:

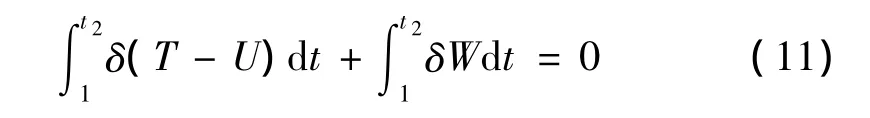
式中，δ为变分符号，T和U分别为整体结构的动能和势能，W为外力功。整体结构的势能变分表示为:

式中:

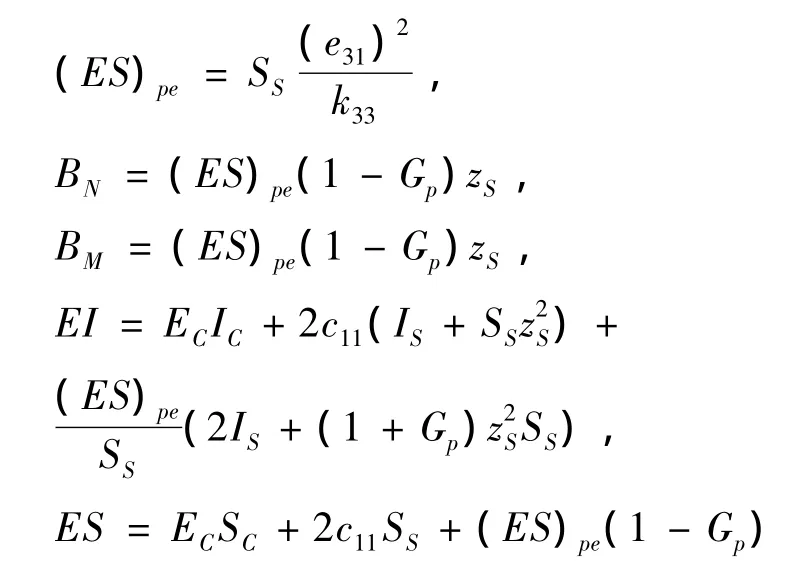
整体结构的动能变分表示为:

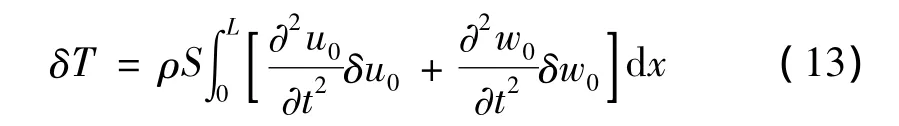
式中，ρS=ρSSS+ρCSC+ ρASA。

整体结构的外力功变分表示为

式中，p表示夹层梁左端所受的轴向力。

将式(12)、式(13)、式(14)代入式(11)中，不计轴向变形的影响，经过一系列变分运算并略去高阶微量，得到夹层梁整体结构的运动方程:

研究中只考虑夹层梁的一阶横向振动模态，可将w0表示成如下形式:

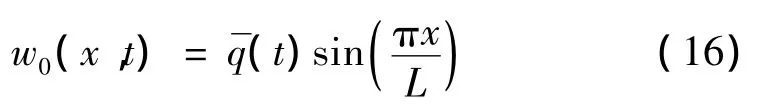
将式(16)代入式(15)中，并引入轴向力 p=p0+，进行Galerkin积分得到:

式中:

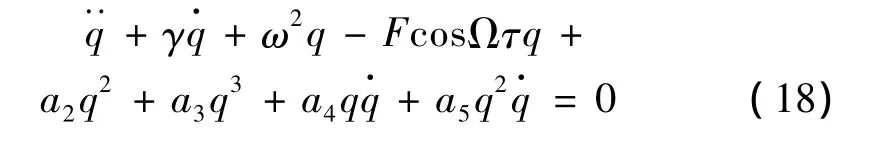
式中:

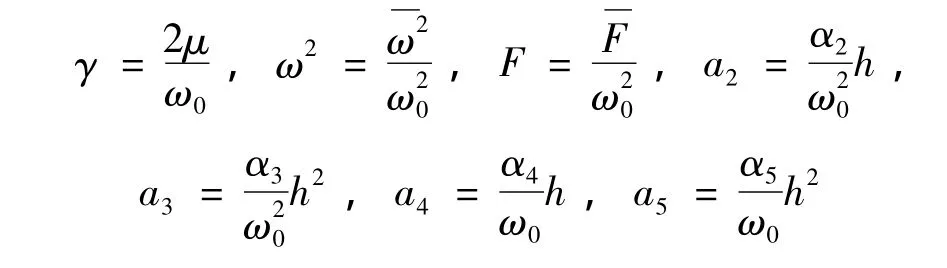
3 数值仿真

针对压电夹层梁的无量纲动力学方程(18)，利用四阶龙格库塔法对其模拟分析，得到系统的非线性动力学响应。所取夹层梁的物理参数和几何参数见表1。

表1 压电夹层梁的几何尺寸与材料物理性质Tab.1 Geometrical material properties of the piezoeletric sandwich beams

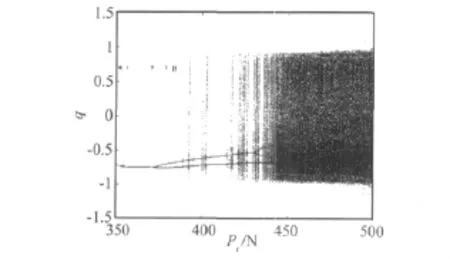
图2 轴向激励分岔图Fig.2 The bifurcation for the axial load of pt

图2 是系统响应随着轴向激励变化的分岔图，其中静态轴向力 p0=400 N，Gd=0.001 s，Gp=0.1。图3～图5各自分别给出了系统不同响应状态下的时间历程图(a)，相图(b)和Poincare映射图(c)。从图2中可看出，随着轴向激励的增大，系统经历了从周期→倍周期→混沌的分岔运动过程。改变图2中外激励pt，其他条件不变，当pt=350 N时，系统表现为周期运动如图3所示。当增大轴向激励为pt=380 N，系统由周期运动变为二倍周期运动，如图4所示。继续增大轴向激励，从图2中可看出系统经倍周期分岔发生混沌运动，如图5所示，其中(c)图的Poincare映射表现出明显的混沌特征。

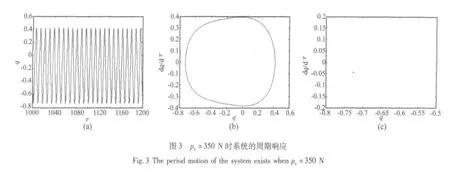
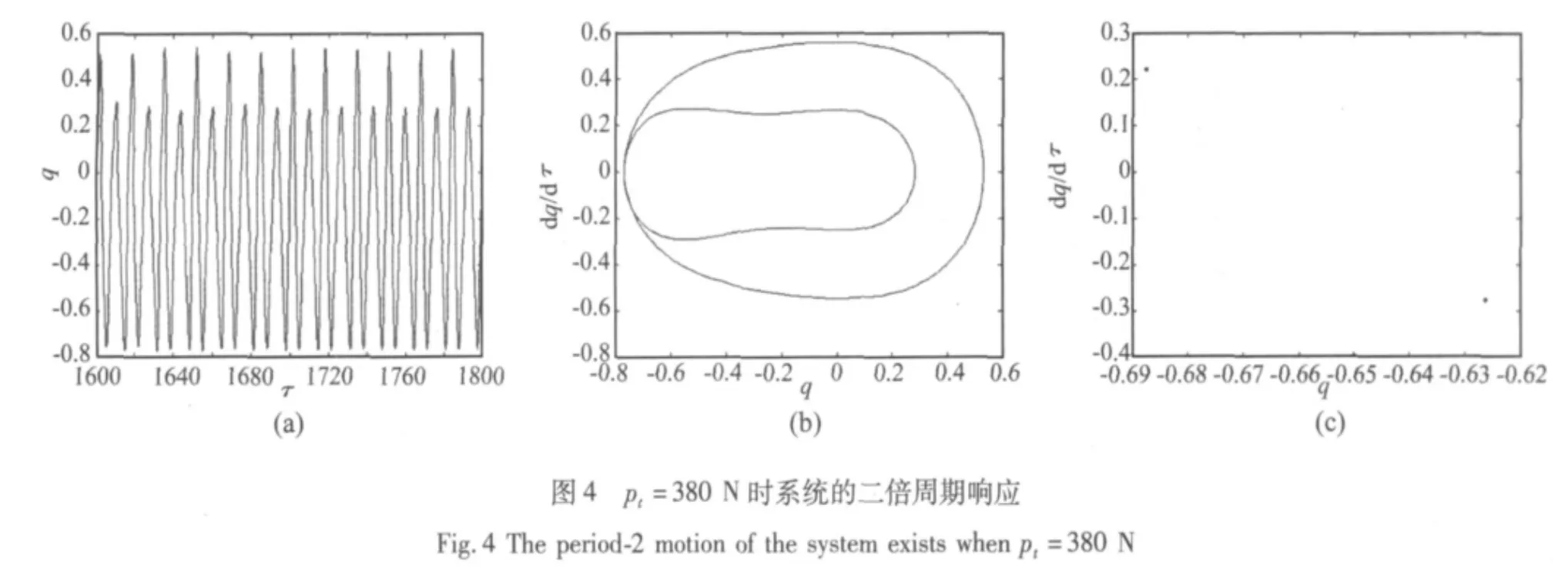
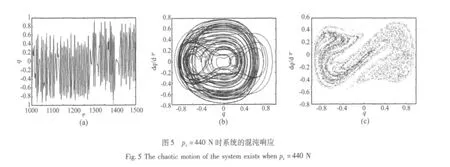
为了研究压电层的振动控制，图6和图7分别给出了闭环状态下电势微分增益Gd和电势比例增益Gp的分岔图，其中轴向激励pt=480 N，系统发生混沌响应。从图6中可以看出，随着电势微分增益的增大，系统经历了混沌→倍周期→周期的过程，可阻止系统通过倍周期分岔进入混沌运动，保持了系统的稳定性有着明显的控制效果。图7显示了电势比例增益Gp对夹层梁混沌运动的控制效果。电势比例增益Gp的增大可以抑制系统发生混沌运动，使系统发生倍周期或周期响应，控制效果也十分明显，保持了系统的稳定性与可控性。

图6 电势微分增益Gd的分岔图Fig.6 The bifurcation for the gain derivative potential Gd

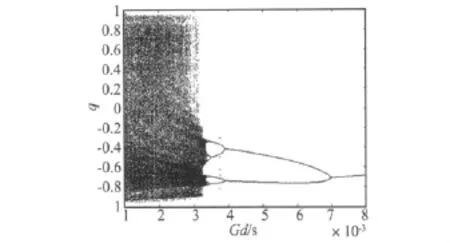
图7 电势比例增益Gd的分岔图Fig.7 The bifurcation for the gain proportional potential Gp

4 结论

以简支压电夹层梁为研究对象，研究了在轴向参数激励下夹层梁的非线性横向振动。基于von Karman理论和比例微分控制策略，运用Hamilton原理推导出了压电夹层梁的动力学方程。用数值方法研究了压电夹层梁的非线性动力学、混沌动力学响应。

通过时间历程图、相图、Poincare映射图和分岔图分析了压电夹层梁的非线性振动响应、动态分岔参数值以及压电控制效果，系统的响应经历了周期、倍周期、混沌的过程。结果表明，在一定参数范围内，系统的响应为周期运动。当系统发生混沌响应时，通过改变电势比例增益和电势微分增益，均可控制压电夹层梁的振动从混沌→倍周期→周期，控制系统产生倍周期分岔解，阻止系统通过倍周期分岔进入混沌运动，保持了系统的稳定性与可控性。

［1] Sun B，Huang D.On the feedback control gain of smart laminated beams，plates and shells［J] .The 6th international Conference on Composite Engineering(ICEE/6)，1999，859－860.

［2] Huang D，Sun B.Approximate analytical solutions of smart composite mindlin beams［J] . Journal of Sound and Vibration，2001，244(3):379－394.

［3] Chen L W，Lin C Y，Wang C C.Dynamic stability analysis and control of a composite beam with piezoelectric layers［J] .Composite and Structures，2002，56(1):97 －109.

［4] Gao JX，Shen Y P.Active control of geometrically nonlinear transient vibration of composite plates with piezoelectric actuators［J] . Journal of Sound and Vibration，2003，264(4):911－928.

［5] Moita J M S，Soares C M M，Soares C A M.Geometrically nonlinear analysis of composite structures with integrated piezoelectric sensors and actuators［J] .Composite and Structures 2002，57(1－4):253－261.

［6] 董兴建，孟 光.压电悬臂梁的动力学建模与主动控制［J] .振动与冲击，2005，24(6):54－57.

［7] Akl W，Poh S，Baz A.Wireless and distributed sensing of the shape of morphing structures［J] .Sensors and Actuators，2007，140(1):94－102.

［8] 李凤明，孙家春，王毅泽，等.参数激励非线性压电梁的振动稳定性［J] .振动工程学报，2008，21(5):441－455.

［9] 傅衣铭，阮建力.具损伤压电智能层合板的非线性主动控制和损伤监测［J] .应用数学和力学，2008，29(4):379－392.

［10] Belouettar S，Azrar L，Daya E M，et al.Active control of nonlinear vibration of sandwich piezoelectric beams:A simplified approach［J] .Computers and Structures，2008，86(3－5):386－397.

［11] 姚志刚，张 伟，陈丽华.压电复合材料层合梁的分岔、混沌动力学与控制［J] .力学学报，2009，41(1):130－140.

［12] 高美娟，张 伟，姚明辉，等.压电复合材料层和板的混沌动力学研究［J] .振动与冲击，2009，28(6):82－85.