基于耦合信号包络分析的引线键合点剪切强度识别方法研究

冯武卫， 孟庆丰

（1.浙江海洋学院机电工程学院，舟山 316000；2.西安交通大学 机械学院轴承研究所，西安 710049）

键合点的抗剪切破坏强度是衡量键合质量的重要指标之一。由于任何一个键合点的缺陷都可能导致整个集成电路的失效，因此，深入研究键合点剪切强度自动检测技术，对确保集成电路安全可靠运行具有十分重要的意义。

近年来，国内外针对键合点质量自动识别技术的研究发展迅速，主要是检测键合过程信息，如键合接触区域摩擦应力、键合工具振动、聚能器变形和换能器振动等，通过相应的特征提取与模式识别技术，进而识别键合强度［1－10］。但是由于严格的传感器安装要求以及传感器与键合系统之间的相互影响制约了这些技术在工厂的实际应用。此外，在信号特征提取方面，现有的技术主要有：采用快速傅里叶变换提取信号幅频特征［5］、通过滤波提取信号的二次谐波信号［6］、利用 Hilbert变换计算键合系统阻抗特征［6］、利用时－频分析方法提取时频分布等高线的面积［7］、计算信号的包络能量［9］等，并取得了良好的效果。但由于键合信号的瞬态特性，现有技术在刻画键合信号局部细微变化方面存在不足，不利于对键合强度的精确识别。

超声波发生器驱动电信号与键合强度有密切联系［10］，已引起高度关注。本文采用检测键合过程中超声波发生器电压和电流信号作为信息载体，并提出了基于键合信号子频带包络分段特征提取方法。通过对实验数据进行分析，结果验证了本文方法的有效性。

1 检测方法原理

压电换能器是引线键合系统的关键设备，由于其核心构件压电晶体的双向压电效应，使得换能器既是一个执行器，也具有传感器的功能。首先，基于压电晶体的反向压电效应，压电换能器作为一个执行器来完成超声波电能到机械能（机械振动）的转换；其次，基于压电晶体的正向压电效应，压电换能器同时也具有传感器功能，在键合过程中，随着键合界面机械、材料属性的变化，键合工具尖端的振动状况持续发生细微变化，经由键合工具和聚能器的传递，这个变化被感应到压电晶体，并直接影响到超声波发生器的电信号。由于键合工具的振动变化是影响键合点形成的关键，与键合强度之间存在内在关系，因此，通过检测超声波发生器的电信号，我们能够提取键合工具尖端细微的振动变化，并通过特征提取与模式识别技术建立键合强度与超声电信号之间的相互关系。

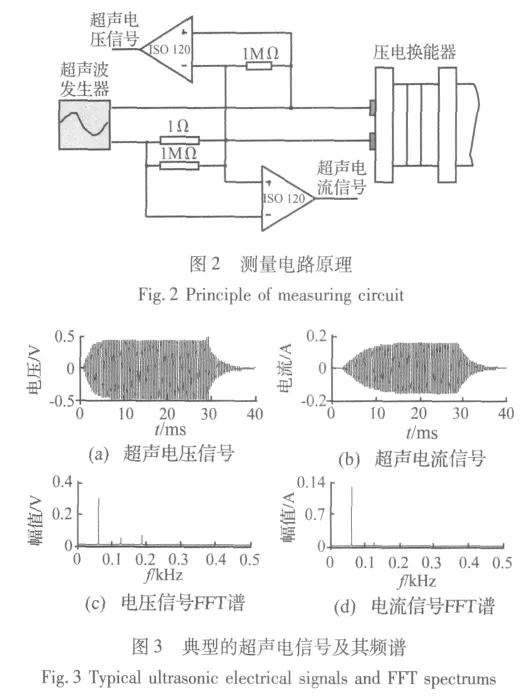
键合强度检测原理如图1所示。首先，为了避免键合系统与数据采集系统间的相互影响，在信号采集系统的前端安装专用测量电路（见图2），其中电压和电流信号分别通过在测量电路中并联1 MΩ和串联高精度1 Ω电阻来获取。采样频率为1 MHz，采样时间为40 ms。为了捕获瞬态超声键合信号，采集程序中触发方式设置为前触发，触发信号选为电压信号，触发值设置为0.03 V。当电压信号超过触发值时，采集系统将对电压和电流信号进行同时采集，并保留触发前2 ms的数据。通过现代信号分析处理方法对超声电压和电流信号进行特征提取、模式识别和质量检测。

图3是键合过程中采集的一组超声电压和电流信号以及相应的频谱，这些信号都是典型的瞬态信号，持续时间极短（约30 ms～40 ms）。因此，采用传统的频谱分析方法无法将键合过程中各个阶段的时变信息反映出来。采用联合时频分析方法虽然能够同时提供信号的时域和频域信息，但由于其固有的时频分辨率的制约，仍然难以将瞬态的微弱故障特征精确地刻画出来。键合瞬态超声信号的包络可以明显地反映键合过程的状态变化情况，已引起广泛关注［3，9］。然而，如何从包络波形上提取键合过程的细微变化仍是一个有待解决的关键问题。Michael在早期键合机理研究中，从冶金学角度将键合过程分为“去除键合接触面氧化膜、键合点塑性变形和应力扩散”［9］，揭示了键合点形成的三个关键的物理过程。对应到超声电信号包络上，这三个物理过程分别体现在信号的上升、稳定和衰减三个阶段，由于每个阶段对键合质量的贡献以及作用机理不同，其波形特征也必然不同。此外，从电压和电流信号FFT谱图［图4（c）和（d）］我们还可以看出，超声电信号的能量主要集中在前三阶倍频中，在特征提取过程中，为了反映信号在频域上的变化，须进行滤波细化处理。

2 超声电信号特征提取方法

针对超声电信号，首先，通过一个带通滤波器组，提取信号的基频和高次谐波信号；然后，利用Hilbert变换，获取各子频带信号包络；最后，各子频带信号被分别分成三个阶段进行特征提取。特征提取之后，为了消除冗余信息和实现特征降维，主分量分析方法被用来进行特征选择。

2.1 超声电信号滤波

为了提取超声电信号各子频带信号，本文设计了一个带通滤波器组，它包含3个子滤波器，子滤波器的中心频率分别是超声信号基频、二次谐波和三次谐波频率（可以通过傅里叶变换来获取）。

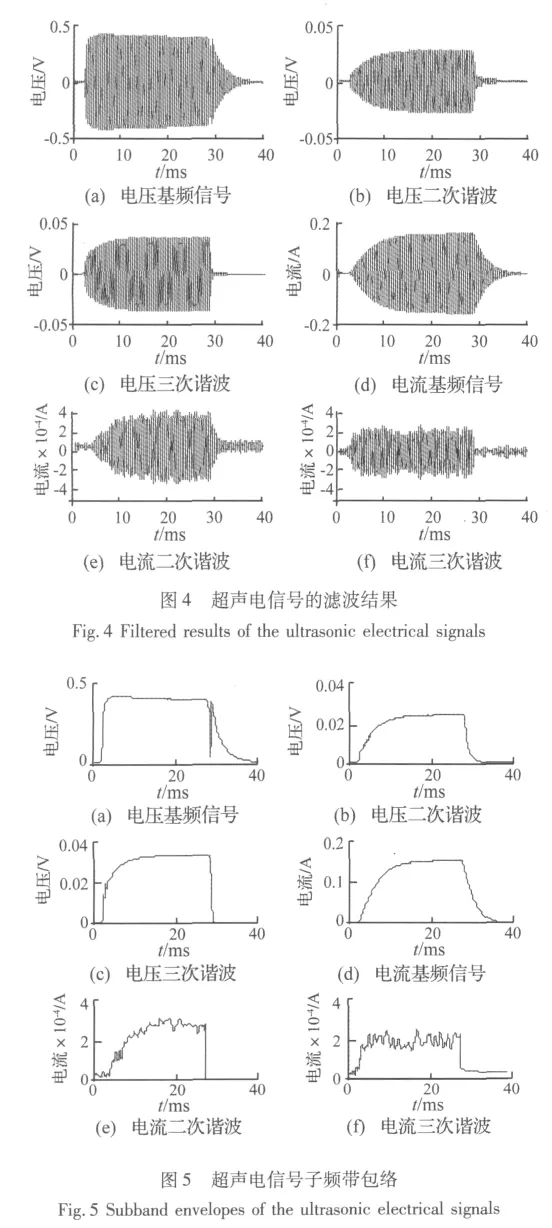
对于图3给出的典型超声电信号，通过上述设计的滤波器组滤波后结果如图4所示。可以看出，每个子频带信号波形各不相同，反映出超声电信号各子频带的变化特征。

2.2 包络计算

文献［6］利用Hilbert变换获取了超声电压和电流信号的包络并计算了键合系统的阻抗，取得了良好的效果。因此，本文利用Hilbert变换进行计算信号的包络，针对超声键合信号，设y（t）是某个子频带信号，它的Hilbert变换可表示为

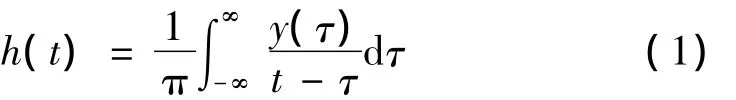
信号的包络为：

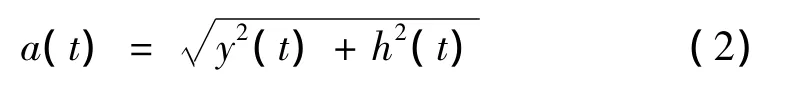
图5给出了各子频带信号的包络，可以看出，Hilbert变换在计算信号包络上的有效性。

2.3 分段特征提取

本文以超声电压信号基频包络为例进行包络分段和特征提取，如图6所示。超声电压和电流信号的其它子频带包络分段原则与电压基频包络一致。

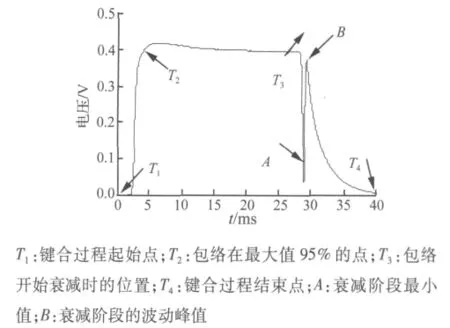
图6 电压信号基频包络分段原理Fig.6 Segmentation principle of fundamental envelope of voltage

2.3.1 电压基频包络上升阶段（T1～T2）的特征提取

在包络上升阶段，信号表现为持续上升，键合接触面氧化膜被逐渐破坏。对于不同的键合样本，由于其接触面质量和氧化程度不同，因此反应到超声信号上，上升的幅度以及上升的速率也会不同。在这个阶段，从包络信号上我们提取了3个特征量来反映这些变化，特征描述和方程如表1。

表1 电压基频包络上升阶段的特征Tab.1 Features and equations for the rising phase

2.3.2 电压基频包络稳定阶段（T2～T3）的特征提取

在包络稳定阶段，信号表现为小范围波动。当键合接触面受到污染时，包络的波形会反应出较大的波动，其波动程度反应了引线与基板的接触摩擦状况，一些统计可以反映出这些波动程度。因此，为了获取这些细微的波动变化，提取了11个统计量来表征包络的波动程度，特征和方程如表2。

2.3.3 电压基频包络衰减阶段（T3～T4）的特征提取在包络衰减阶段，信号表现为振荡衰减，键合接触面内应力逐渐减小，键合点基本形成，其衰减速度及其幅度同样能够反应出键合点的接触摩擦状况。本文提取了5个特征量来描述此阶段的衰减特性，详细描述如表3。

表2 电压基频包络稳定阶段的特征Tab.2 Features and equations for the stable phase

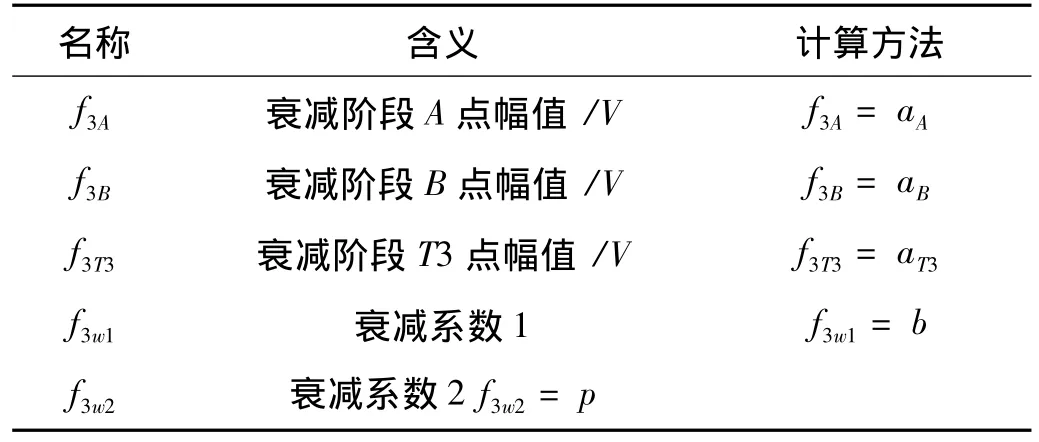
表3 电压基频包络衰减阶段的特征和方程Tab.3 Features and equations for the damping phase

设f（t）是衰减阶段点B到T4阶段的包络数据，则表3中衰减系数可以通过如下方程来拟合

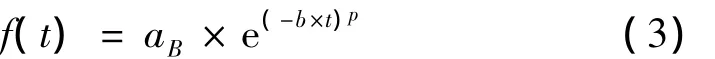
其中，f（t）是点B到T4阶段的包络数据（参见图6），本文利用最小二乘法来估计两个衰减系数b，p。

对于其它的子频带信号，特征提取方法与电压基频包络相似。最终，利用本文的方法，从超声电压和电流包络上一共提取了115个特征量，其中包含每个子频带包络提取19个特征（19×6=114）和一个基频频率特征。并以这些特征量来表征一个键合过程。

2.4 特征选择

具体提取的特征量之间可能存在相关性，为了消除特征间的相关性并实现特征降维，通常需要进行特征选择。本文选择主分量分析方法进行特征选择，设X=［x1，x2，…，xn］T是原始特征矩阵，n是特征变量的维数。主分量计算过程如下：

2.4.1 特征向量归一化

设Y=［y1，y2，…，yi，…，yn］是归一化特征矩阵，其中yi，（i=1，2，…，n）可以表示为：

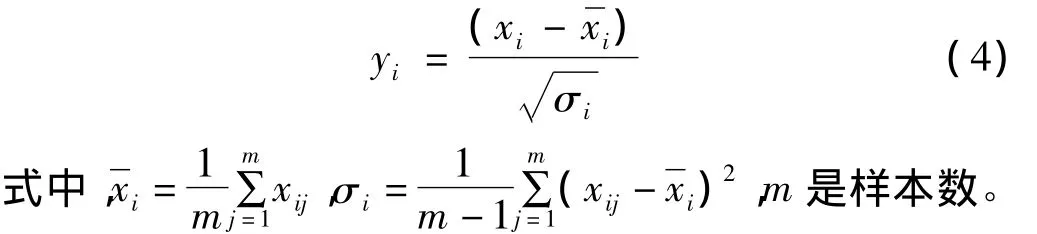
2.4.2 主分量计算

设 ξi，i=1，2，…，n，是归一化矩阵Y的线性组合，可以寻找正交转换矩阵A来计算新特征变量ξi：

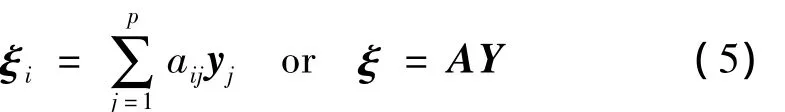
为了计算ξ，首先，我们能获得归一化矩阵Y的协方差阵R=（rij）n×n：

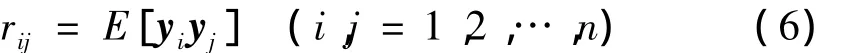
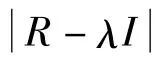
可以证明，矩阵A=（a1，a2，…，ai）是一个正交化矩阵，且能够满足主分量分析的要求。其主分量（PC）可以表示为：

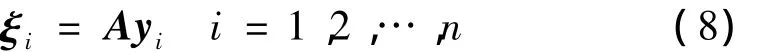
2.4.3 主分量选择

为了评估主分量的有效性和实现特征降维，这里引入两个参数，一个是特征分量贡献率κ，一个是累积贡献率ζ

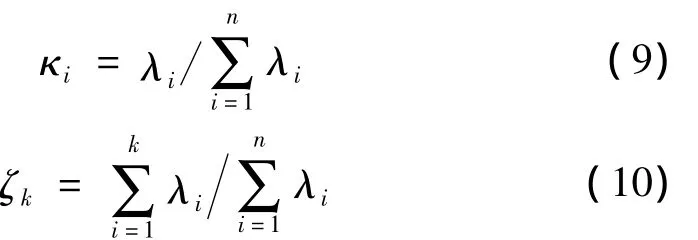
主分量贡献率代表某个主分量占有原始信息量的比重，如果累积贡献率ζk达到90%以上，就可以利用前k个主分量代替原始特征变量，实现特征降维。

3 键合点剪切强度识别

本文获取了一些具有不同剪切破坏强度的键合点，实验台由深圳天力精密系统的MG10半自动球键合机改装而成，工作频率为62.5 kHz，引线为25 um金线，键合机工艺参数设置如下：键合力：147 mN，键合功率30 mW，键合时间：40 ms，加热温度：200℃。

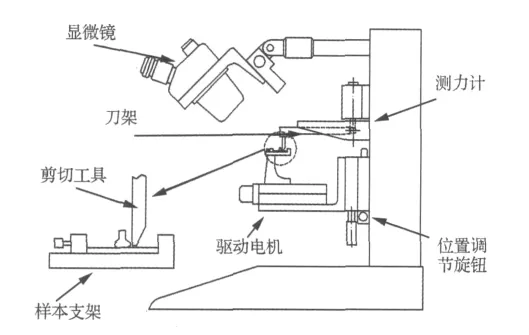
图7 键合点剪切强度测试仪Fig.7 Sketch of a precision bond shear strength tester

键合过程完成后，我们可以通过如图7所示的测试仪来测试键合点剪切强度。其主要原理是：在显微镜下调整键合点位置，使剪切工具尖端对准键合点球面的中部。然后键合点在驱动电机匀速驱动下，发生剪切破坏，并同时记录剪切工具测试力，即为键合点剪切强度。图8给出了两个典型的被剪切测试后键合点电镜扫描图片，其中图8（a）是好的键合点（剪切强度=128 mN），图8（b）是弱连接强度键合点（剪切强度=25 mN）。可以看出，好的键合点剪切测试过程中剪切断裂面发生在键合球的中部，而弱连接强度键合点直接从根部剪断。产生弱连接强度主要是由于键合基板表面受污染，我们通过在键合基板上粘附金属颗粒来模拟键合表面受污染状况。

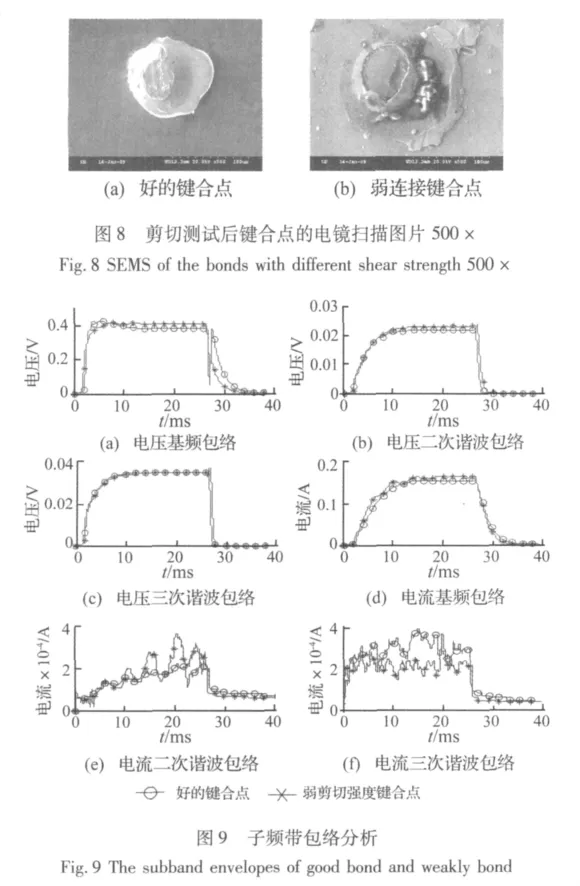
利用本文特征提取方法对上述两种键合样本超声电信号进行处理，图9给出了各子频带包络分析结果。直接通过子频带包络区分键合强度的大小有一定难度，且精度不宜保证，然而，当子频带信号被分段处理后，其变化特征被明显的展现出来（图10）。除了上升阶段上升速度、稳定阶段幅值和衰减阶段衰减速度有明显差异外，弱连接强度键合点各子频带稳定阶段包络存在剧烈波动。表4给出了几个区分不同键合强度键合点相对敏感的特征，定量的体现了本文特征提取方法的有效性。

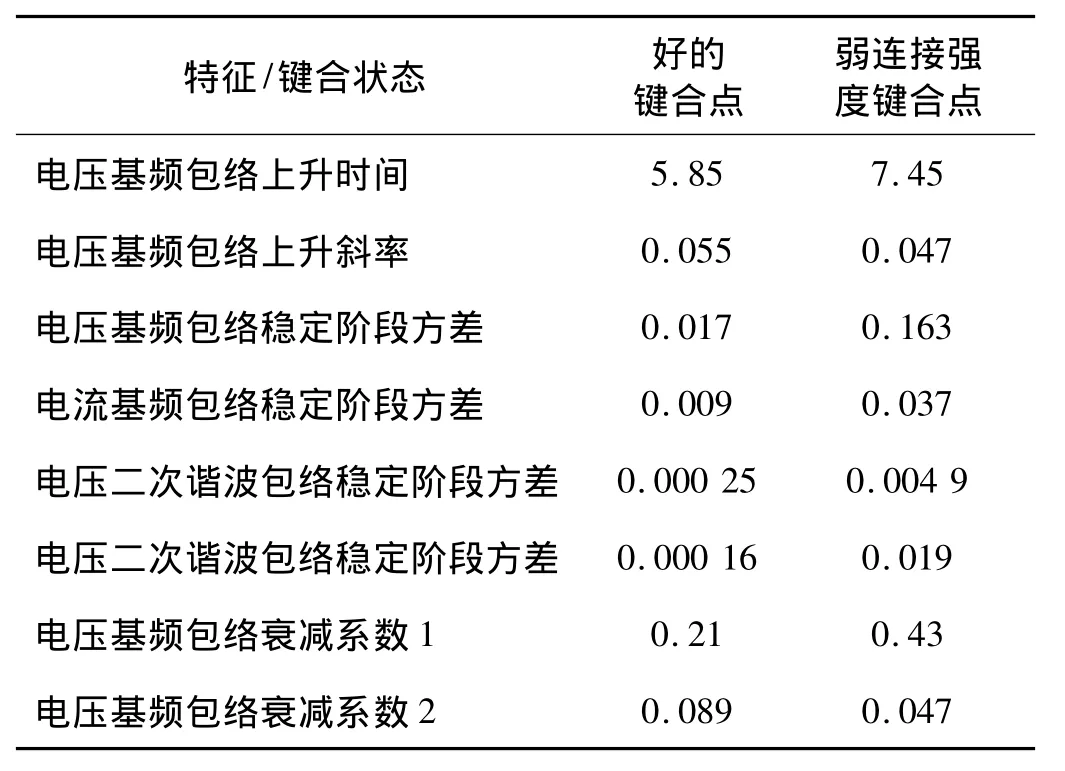
表4 区分弱连接强度键合点的敏感特征Tab.4 Sensitive features for distinguishing the weakly bond

本文总共获取了360个键合点，其中包括120个受污染键合点和240个好的键合点，好的键合点强度从78 mN到128 mN，受污染的键合点强度从19 mN到78 mN。利用本文特征提取方法对上述360个实验样本信号进行特征提取和主分量计算，表5给出了前15个主分量贡献率，本文选择前13个主分量作为识别键合剪切强度的特征，在保证充足原始特征信息的前提下实现特征降维。

鉴于提取的主分量与键合强度之间的复杂关系，本文构建了人工神经网络来识别键合点的强度，网络的输入为提取的13个主分量，输出为键合点强度。图11给出了神经网络的结构，它包含一个输入层，一个隐层和一个输出层，隐层的节点数为15，隐层的激活函数选择sigmoid函数，输出层选择线性函数。首先利用200个实验数据对（130个好的键合点数据和70个受污染的键合点）进行网络训练，循环步数设置为1 000，训练完成后，其均方误差达到0.9 mN。

图10 子频带包络分段分析Fig.10 The segmentation results of every subband signal

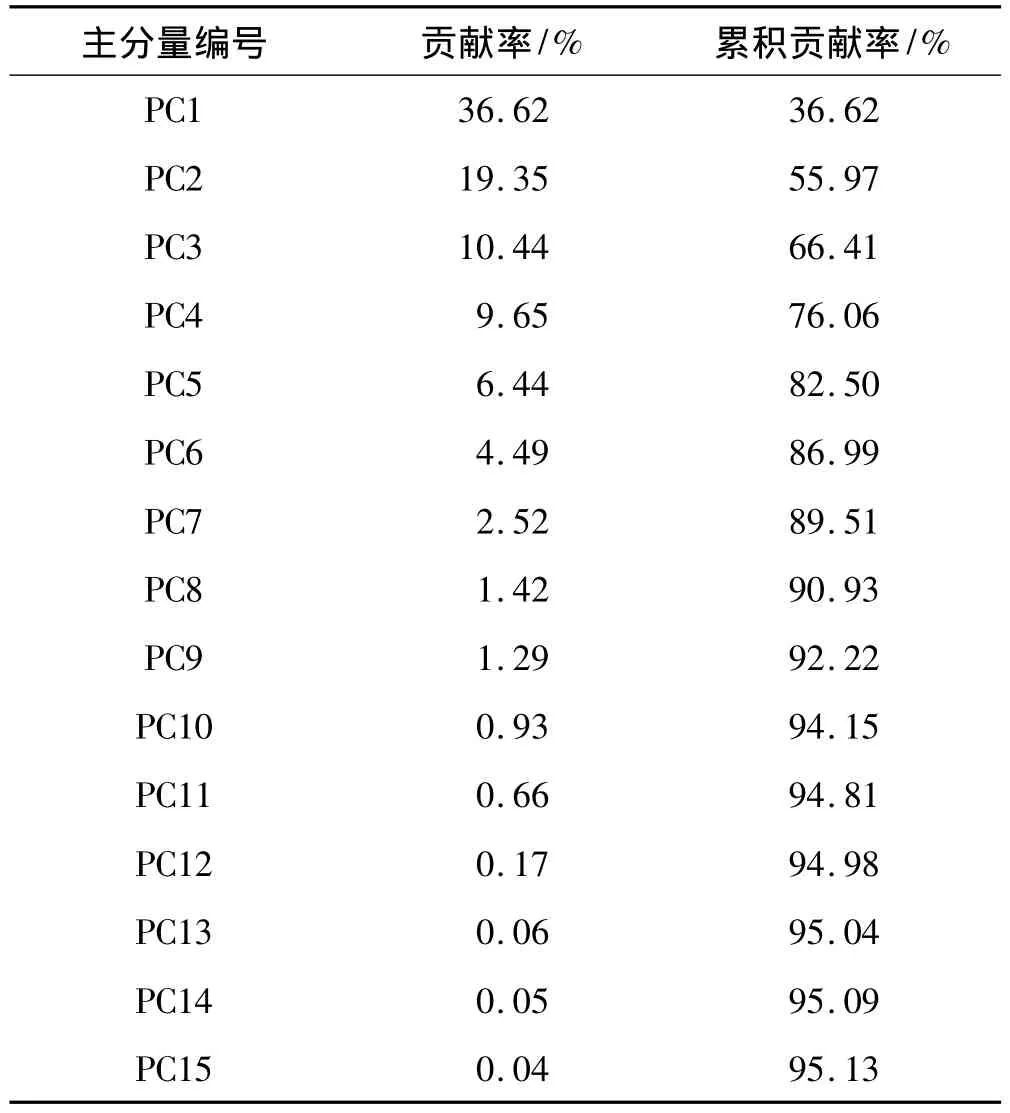
表5 主分量贡献率Tab.5 Principal component contribution rate

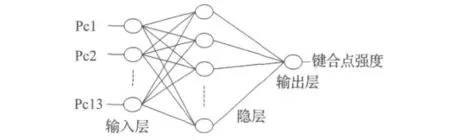
图11 神经网络结构Fig.11 The structure of ANN

为了检测网络的有效性，其余的160个键合样本对作为验证数据输入网络进行测试，测试结果的均方误差是1.4mN。图12给出了预测结果，尽管有一些数据误差比较大，然而，预测结果的趋势有效的验证了本文特征提取方法的有效性与可行性。

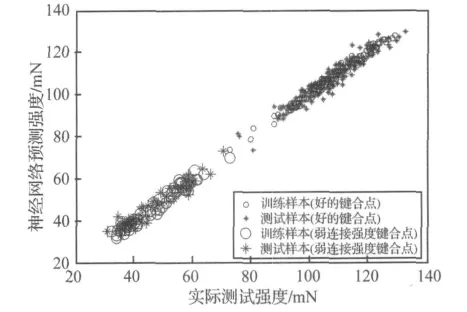
图12 神经网络训练和预测结果Fig.12 ANN predicting bond shear strength

4 结论

本研究主要完成了3个方面的工作。首先，利用专用测量电路，采集了键合系统超声波电压和电流信号；其次，利用本文的特征提取方法，提取了115个特征量，并通过主分量分析进行特征选择。最后，通过对实验数据分析，验证了本文所提出的键合点剪切强度识别方法的有效性。此外，本方法还存在以下优点，首先，它属于无传感器检测技术，避免了传感器安装困难及其传感器与键合系统的相互影响。第二，相应的信号处理及特征提取方法容易实现，为键合质量在线检测提供了一条新途径。

［1］Mcbrearty M，Kim L H，Bilgutay M.Analysis of inpedance loading in ultrasonic transducer systems［C］//Proc of 2006 Ultrasonics Symposium.Chicago，USA，2006：497－502.

［2］Khotanzad A，Banerjee H，Srinath M D.A vision system for inspection of ball bonds and 2－D profile of bonding wires in integrated circuits［J］.IEEE Trans.on Semiconductor Manufacturing，1994，7（4）：413 －422.

［3］ Lee H K，Yoo S I.A method for inspection of ball bonds in integrated circuits［C］//IEEE SMC’99 Conference Proceedings.Tokyo，Japen：IEEE，1999：975 －980.

［4］ Schwaller P，Groning P，Schneuwly A，et al.Surface and friction characterization by thermoelectric measurements during ultrasonic friction processes［J］.Ultrasonics，2000，38（1－8）：212－214.

［5］Or S W，H L，Chan W.Ultrasonic wire-bond quality monitoring using piezoelectric sensor［J］.Sens.Actuators A，1998，65（1）：69－75.

［6］Zhang D.Study of mechanism of ultrasonic wire bonding process［D］.Nanyang Techno.Univ.，Singapore，2002.

［7］Zhang D，Ling S F.Monitoring wire bonding via timefrequency analysis of horn vibration［J］.IEEE Trans.Electron.Package Manuf.，2003，26（3）：216 －220.

［8］Paul W P C，Li H L.Smart ultrasonic transducer for wire bonding applications［J］.Materials Chemistry and Physics，2002，75（1－3）：95－100.

［9］Micheal B，Jorg W C，Hans H.Bond process monitoring via self-sensing piezoelectric transducers［C］.IEEE International Ultrasonics，Ferroelectrics，and frequency Control joint 50th AnniversaryConference. SanJose， CA：IEEE， 2004：125－129.

［10］ Pufall R.Automatic process control of wire bonding［C］//Proc.Electron.Compon.Techno.Conf.，1993：159－162.