密肋复合墙-剪力墙混合结构水平位移计算方法研究
郭 猛,袁 泉,黄 炜,张旭锋,李鹏飞
(1.北京交通大学 土木建筑工程学院,北京 100044;2.西安建筑科技大学 土木工程学院,西安 710055)
为了进一步提高在基本烈度为7度地震区建造密肋复合墙结构的层数和建筑总高度,解决基本烈度为8度地震区建造超过现有《密肋壁板结构技术规程》[1]中有关密肋结构总层数和总高度的限制问题,课题组近期提出了密肋复合墙-RC剪力墙混合结构[2-5](简称复合墙-剪力墙结构),如图1所示。这种新型混合结构以密肋复合墙为主体,根据计算需要设置一定数量RC剪力墙,通过框架梁、连梁或楼板将密肋复合墙与混凝土墙联合起来,共同抵御水平荷载作用,其中剪力墙可以是实体墙、带缝墙、开洞墙等。由于混合结构的大部分抗侧力构件为密肋复合墙,因而保持了密肋结构的诸多长处;同时由于加入部分剪力墙,增大了结构极限承载力和抗侧刚度,减小了地震作用下楼层层间变形值,从而提高了密肋结构的整体抗震能力。剪力墙与复合墙变形机制的不同使得混合结构呈现双重延性受力特点,即小震时剪力墙作为第一道防线起主要作用,中震和大震时剪力墙刚度出现退化,地震力由密肋复合墙与剪力墙按有效刚度分担。作为试点工程,密肋复合墙-剪力墙混合结构体系已在宁夏银川等地区的部队营房建筑中得 到应用。
对于水平荷载下密肋复合墙-剪力墙结构位移的研究:文献[6]建立了考虑复合墙弹性常数取值特点与剪切变形的密肋结构位移方程;文献[2]从能量原理出发,通过推导结构体系的系统势能方程和约束方程,构造辅助泛函并依据变分原理,得出混合结构的水平位移计算公式。基于能量的位移计算方法的主要缺点是需要多次试算构造出合理的辅助泛函,不同泛函形式决定了最终位移的不同计算精度。
本文简要分析了复合墙-剪力墙混合结构的协同工作机制,依据密肋复合墙的弯剪型特点,采用经典的变形连续化协同工作方法,建立结构体系的位移微分方程,推导其水平位移的解析解,并通过算例分析混合结构的变形特点。

图1 密肋复合墙-剪力墙混合结构Fig.1 Multi-grid composite wall-shear wall structure
1 复合墙-剪力墙结构协同工作机制
单独承受水平荷载作用时密肋复合墙与剪力墙的变形特点不同:剪力墙以弯曲变形为主,中高层剪力墙一般忽略其剪切变形,随着楼层的增加,总侧移和层间侧移增长较快;密肋复合墙的构造形式决定了墙体的主要弹性常数(Eeq、Geq)是与框格单元截面尺寸、框格布置方式等因素有关的变参数,且Eeq、Geq之间不存在线性的比例关系,变形大致属于弯剪型,以弯曲变形为主还是以剪切变形为主取决于墙体抗弯刚度和抗剪刚度的相对大小。
复合墙-剪力墙混合结构中,框架梁、连梁或楼板把两种墙肢联系在一起,使得二者在各层楼板处协调变形。由于密肋复合墙存在剪切变形,但比框架结构要小得多,因此密肋复合墙-剪力墙结构的层间变形介于框架-剪力墙结构和剪力墙结构之间,小于框剪结构而大于剪力墙结构,与结构的刚度特征值有关。同时,由于复合墙单元的抗侧刚度大于框架,以往由剪力墙担负大部分外荷载的情况,变成由密肋复合墙与剪力墙共同承担,连梁的协同作用相对于框架-剪力墙结构而言要小的多,这是与框架-剪力墙结构的重要区别之一。
弹性阶段,复合墙与剪力墙协同工作时各自承担水平荷载的大小取决于两者的侧向刚度之比,但不是一个简单的比例关系,需要首先计算出结构的水平位移,然后根据墙体内力与位移的关系确定复合墙与剪力墙各自分担的剪力、弯矩。
2 复合墙-剪力墙结构水平位移计算
2.1 计算模型
密肋复合墙-剪力墙混合结构中,不考虑剪力墙的剪切变形,考虑密肋复合墙则的弯曲变形和剪切变形,计算模型如图2所示。当两个子结构变形机制不同时,选定不同的子结构为分析对象,得出的位移微分方程在表达形式上有所不同,计算的繁简程度亦有所区别,应以方便计算为原则选择合适的分析对象。本文选择密肋复合墙作为子结构1,以其为隔离体建立位移微分方程及进行水平位移公式的推导。

图2 复合墙-剪力墙结构计算模型Fig.2 Calculating model of the structure
2.2 基本微分方程
如图2(a)所示,子结构1(密肋复合墙)的变形由弯曲变形yb1和剪切变形yq1两部分组成,根据Timoshenko剪切梁的弯曲变形、剪切变形与外荷载的基本关系[7]列出方程为:
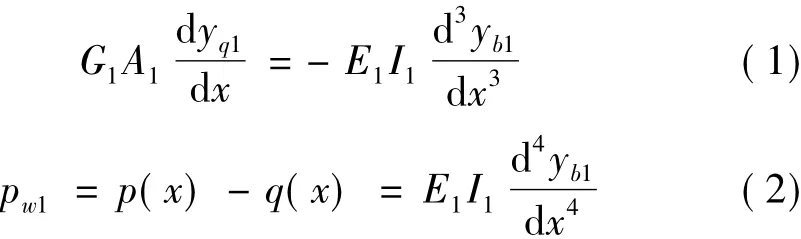
对于子结构2(剪力墙),其荷载与变形的关系为

式中,E1I1、G1A1为子结构1的抗弯刚度、抗剪刚度,E2I2为子结构2的抗弯刚度,q(x)为两个子结构之间的相互作用。
将式(3)代入式(2)得:

两个子结构在任意位置的总水平位移相等,即yb2=yb1+yq1,代入上式消去yb2得:

将式(1)两边对x微分三次,代入式(5)消去yq1

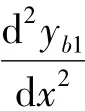


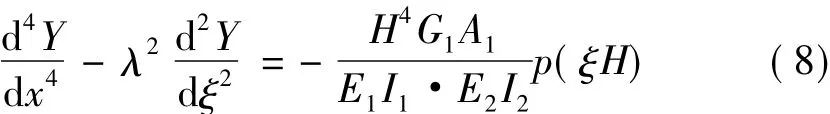
此式即为密肋复合墙-剪力墙混合结构的基本位移微分方程,理论上适用于密肋复合墙的抗弯刚度、抗剪刚度任意变化时其弯曲变形的求解。
如图2(b)所示,当选择剪力墙为子结构1,复合墙为子结构2时,得到以剪力墙为隔离体的弯曲变形微分方程见式(9)。比较式(7)与式(9)可知,后者不需要对位移方程使用变量换元法进行中间变量代换,但外荷载项中含有积分常数,需要结合边界条件求得,求解过程相对复杂。


2.3 水平位移的解析解
对于四阶常系数线性微分方程式(8),其解的一般形式为:

式中,C1、C2、C3、C4是待定常数;Y0为微分方程的特解,与外荷载的具体形式有关。
本文以常见倒三角形荷载为代表,给出水平荷载下密肋复合墙-剪力墙混合结构位移的具体推导过程。设倒三角形荷载为p(x)=qx/H=qξ,则式(7)的特解为:

将Y0代入Y得到弯曲变形方程的一般解:

由Y对ξ积分两次得到复合墙弯曲变形yb1的表达式:

通过子结构1弯曲变形与剪切变形的关系得到其剪切变形yq1,由式(1)、式(11)得:

子结构1的弯曲变形与剪切变形之和即为子结构2的变形,同时也为复合墙-剪力墙结构的总水平位移,将yb1、yq1代入yb2=yb1+yq1整理得:

根据图2(a)确定边界条件,并将边界条件写成矩阵表达形式如下

式中:
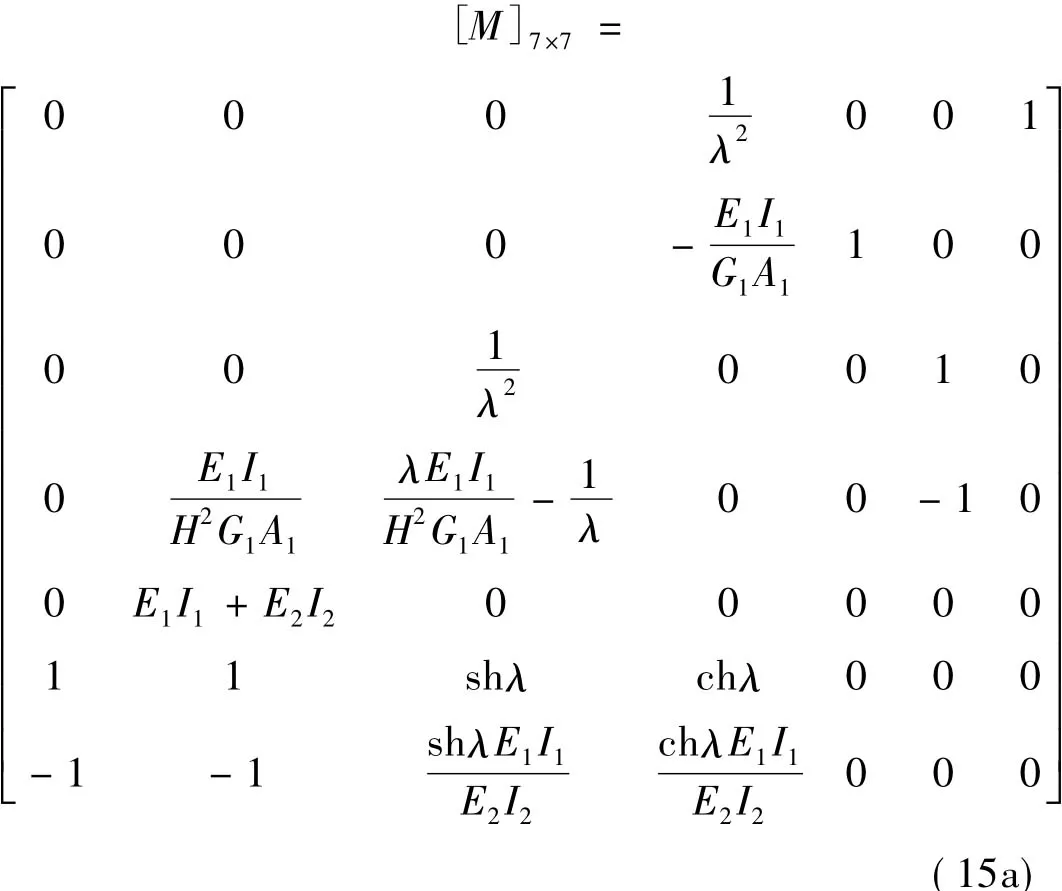

解矩阵方程式(14)得各待定系数为:

将系数C1~C7回代至式(11)~式(13),化简得:

式中,κ=E1I1/H2G1A1。
至此,倒三角形荷载作用下密肋复合墙-剪力墙混合结构中各子结构弯曲变形、剪切变形及结构总水平位移的解析解全部求出。
当混合结构承受均布荷载、顶部集中荷载作用时,位移计算过程与承受倒三角形荷载作用的计算过程基本一致。根据子结构内力与变形关系,可以计算其内力,进而进行墙体截面抗震设计与校核。
3 算例分析
算例1分析复合墙-剪力墙结构与框架-剪力墙结构位移计算公式的相容性。
图2(a)所示的子结构1,当取框架为密肋复合墙的特例时,混合结构转变为一般框架-剪力墙结构,忽略框架部分的弯曲变形,假定其抗弯刚度E1I1→∞,则对混合结构特征值λ进行极限运算得:

对混合结构中密肋复合墙的弯曲变形、剪切变形解析表达式(16)、式(17)进行E1I1→∞的极限运算,且代入式(19)给出的刚度特征值,整理得:
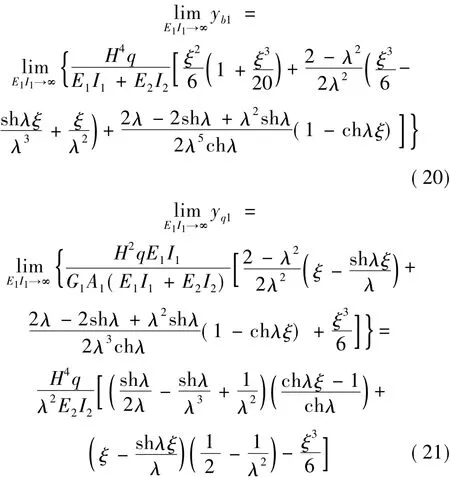
式(19)、式(21)即是人们所熟知的框架-剪力墙结构的刚度特征值和倒三角形荷载下水平位移的计算公式[8]。因此,框架-剪力墙结构可以视为密肋复合墙-剪力墙混合结构在密肋复合墙抗弯刚度取无穷大时的一种特殊表现形式,两者的刚度特征值、位移计算公式是完全相容的。
算例2某10层复合墙-剪力墙结构,层高3.6 m,密肋复合墙、剪力墙厚均为200 mm。复合墙按工程中常用的密肋复合墙构造形式设计,单片墙体抗弯刚度和抗剪刚度为E1I1=6.2 ×1016N·mm2、G1A1=1.1×109N;单片剪力墙抗弯刚度为E2I2=7.9×1016N· mm2;刚度特征值λ=9.9,承受横向倒三角形荷载作用,qmax=100 kN/m。
水平位移计算结果见图3(a),分析可知:结构整体侧移曲线呈现以弯曲变形为主的弯剪型特征,但密肋复合墙体的剪切变形在总变形中占有一定比重,不应忽略,本例中,剪切变形在复合墙下部三层占总变形的比重均超过20%,在三层至六层超过10%。与剪力墙的变形特点比较可知,当剪力墙高宽比>4时,可以忽略其剪切变形的影响,误差不超过10%,而对于复合墙由于其剪切变形较大,高宽比达到6以上时,剪切变形所占比重才减小至20%以下。

图3 算例2位移计算结果Fig.3 Displacement calculation results of example 2
根据混合结构刚度特征值λ的定义,通过调整复合墙与剪力墙数量比例,或者调整复合墙抗弯刚度与抗剪刚度比例的方法,均可改变λ大小。现考察第二种方法对结构变形的影响,复合墙抗剪刚度取为原刚度的0.1倍,其它条件不变,计算结果见图3(b),与图3(a)比较可知:当复合墙抗剪刚度减小时,复合墙自身的剪切变形增大,本例中,复合墙剪切变形明显大于弯曲变形,使得结构整体位移曲线趋近于框架-剪力墙结构的弯剪型特征。
4 结论
(1)分析了复合墙-剪力墙结构的协同工作机制,密肋复合墙的构造特点决定了墙体的抗弯刚度、抗剪刚度是与框格单元截面尺寸、框格构造形式等因素有关的变参数,复合墙剪切变形的计入导致复合墙与剪力墙之间的相互作用更为复杂。
(2)采用变形连续化方法建立了结构体系的位移微分方程,以倒三角形荷载为例推导了复合墙弯曲变形、剪切变形及结构总水平位移的解析表达式。密肋复合墙-剪力墙结构与框剪结构的刚度特征值、位移公式是完全相容的,后者可视为前者在复合墙抗弯刚度取无穷大时的一种特殊表现形式。
(3)一般中高层的复合墙-剪力墙结构侧移曲线呈现弯曲变形为主的弯剪型特征,但复合墙体的剪切变形在总变形中占有一定比重,不应忽略。
(4)本文以密肋复合墙-剪力墙结构为例分析弯剪型(密肋复合墙)-弯曲型(剪力墙)双重抗侧力结构体系的位移计算方法,其思路同样适用于其它弯剪型-弯曲型双重结构体系的位移计算。
[1]河北省建设厅.密肋壁板结构技术规程(DB13(J)64-2006)[S].河北省工程建设标准,2006.
[2]张旭峰.密肋复合墙-剪力墙混合结构协同工作计算分析与实用设计方法研究[D].西安:西安建筑科技大学,2008.
[3] Xia L,Yao Q F,Chang P,et al.Seismic safety evaluation analysis of a new building structure with multi-ribbed composite wall structure[C].Proceedings of International Conference on Earthquake Engineering:The First Anniversary of Wenchuan Earthquake,2009:325-328.
[4]北京交通大学,等.具有多道抗震防线的耗能复合墙结构设计理论与关键技术研究[R].北京:北京交通大学,2009.
[5]黄 炜,张程华,姚谦峰,等.密肋壁板结构简化计算模型对比分析[J].振动与冲击,2009,28(7):187 -191.
[6]郭 猛,姚谦峰,黄 炜,等.水平荷载作用下密肋复合墙结构的变形计算[J].世界地震工程,2009,25(4):12 -17.
[7] Timoshenko S,Gere J.材料力学[M].北京:科学出版社,1990.
[8]包世华,张铜生.高层建筑结构设计和计算[M].北京:清华大学出版社,2005.

