基于GARCH-CVaR与GARCH-VaR的人民币汇率风险测度及效果对比研究

朱新玲，黎 鹏

(1武汉科技大学管理学院，武汉430081;2中南民族大学经济学院，武汉430074)

随着人民币汇率波动频率和幅度的逐步增大，汇率风险日趋增大，对汇率波动风险进行准确度量、控制和防范是汇率波动研究的重要内容.汇率风险属于金融风险，可以用金融风险的度量方法进行测度.VaR是当前金融机构度量金融风险的标准方法，但VaR不满足次可加性，不是一致性风险度量指标［1］，且没有考虑尾部风险，缺乏对极端事件的控制.针对VaR方法的上述缺陷，学者们提出了诸多改进手段试图替代 VaR方法，如:Acerbi和Tasche(2002)［2］的预期短缺 ES，徐绪松(2002)的半绝对离差［3］，李仲飞(2003)的在险收益 EaR［4］等，然而，这些方法或者在理论上不够完善，或者在计算上不够简洁，使其在实际应用中受到较大限制，未得到学术界的广泛认可.2000年 Rockafeller和 Uryasev［5］在对VaR修正的基础上正式提出了条件在险价值(CVaR)的概念，它有效弥补了VaR不满足次可加性、没有考虑尾部风险等缺陷，逐渐受到学者和金融机构的青睐.本文以人民币汇率风险为例探究模型类型、分布假定和置信水平对VaR和CVaR风险测度的影响以及CVaR相对于VaR的优势.

1 VaR及CVaR概述

1.1 VaR及CVaR的概念

(1)VaR(Value at Risk)指处于风险中的价值，一般称为风险价值或在险价值，Jorion P(1996)把VaR定义为:资产在给定的置信水平和持有期下预期的最大损失.即:其中，Δp为资产在持有期内的损失，VaR为置信水平c(一般取为99%、95%、90%)下的风险价值.

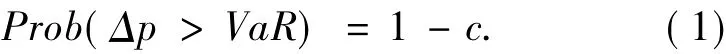
(2)CVaR(Conditional Value at Risk)一般称为条件风险价值，是在一定的置信水平下，某一资产的损失超过VaR的条件均值，反映了损失超过VaR时可能遭受的平均潜在损失，即:

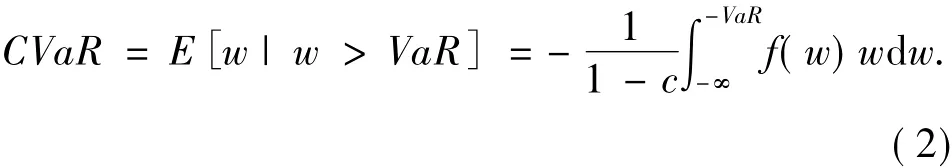
其中，c为置信水平，w为资产或资产组合的损失，f(w)为概率密度函数，VaR为置信水平c下的风险价值.

1.2 VaR及CVaR的计算方法

1.2.1 VaR 的计算方法

利用GARCH族模型计算时变的条件方差ht，将其代入VaR的定义公式(1)，可得基于GARCH族模型的动态VaR计算公式:

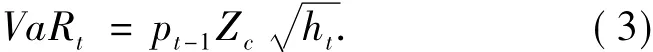
其中，pt－1为t－1日汇率收盘价，Zc为置信水平为c时对应分布函数的分位数，ht为汇率收益率序列的条件方差序列.

1.2.2 CVaR 的计算方法

若用z表示对应于某一置信水平c的分位数，用q表示大于z的分位数，根据CVaR的定义，可得基于GARCH族模型的CVaR计算公式为［6］:

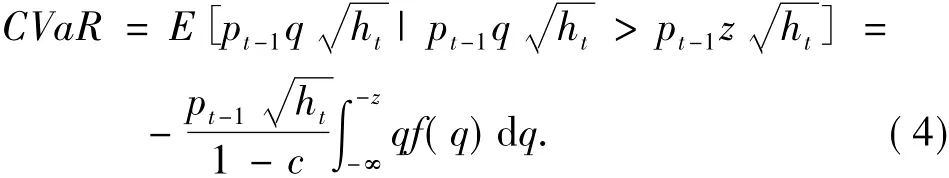
其中pt－1表示第t－1日的汇率收盘价,表示条件方差，f(q)表示汇率收益率序列服从分布的密度函数.将不同分布的密度函数代入可得以下具体的计算公式.

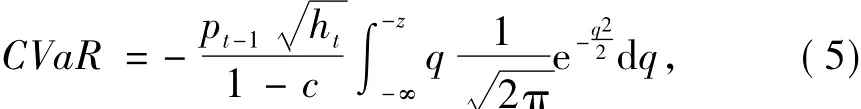
正态分布假定下，CVaR的计算公式为:t分布假定下，若d表示自由度，CVaR的计算公式为:

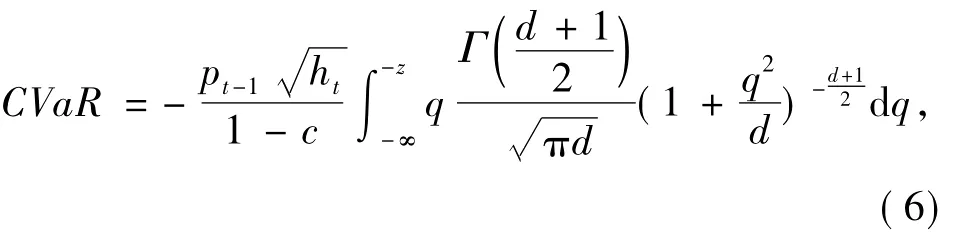
广义误差分布(GED)假定下，若d表示自由度，CVaR的计算公式为:

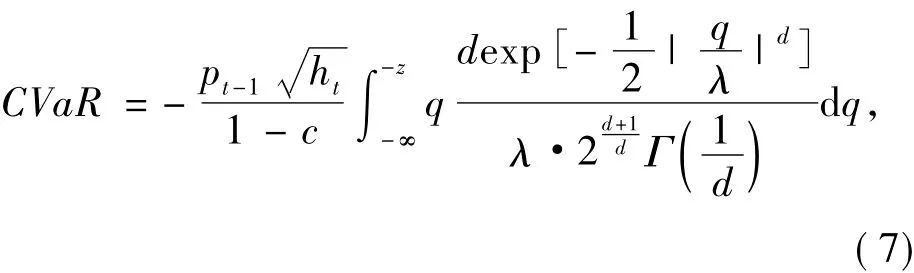
1.3 VaR及CVaR的准确性检验

VaR及CVaR模型的准确性检验是指VaR(CVaR)模型的测量结果对实际损失的覆盖程度.例如，假定估算出95%置信水平下的VaR(CVaR)值，则VaR(CVaR)模型的准确性是指实际损失结果超过VaR(CVaR)值的概率(失败率)是否接近5%.假定计算VaR(CVaR)的置信水平为c，实际考察天数为N，失败天数为m，则失败率为p(m/N)，将p与失败期望概率(1－c)进行比较，若p＞1－c，说明VaR(CVaR)模型低估了风险，若p＜1－c，说明模型结果覆盖了实际损失，但是若p很小，则表明VaR(CVaR)模型的估计过于保守.

1.4 CVaR相对于VaR的优势

CVaR继承了VaR的诸多优点，同时对VaR的缺点进行了修正，具体表现在:

(1)充分控制尾部风险.与VaR相比，CVaR不是单一的分位值点，而是尾部损失的均值，只有将所有大于VaR的损失值全部估算到才能够计算CVaR值，因此，CVaR对尾部损失的测量是充分的;

(2)CVaR具有良好的数学和统计特性.可以证明CVaR满足次可加性、连续性、凸性、单调性等特征，因此，CVaR是一致性风险度量指标，能通过优化的办法求得最小风险投资组合.

2 基于GARCH-VaR及GARCH-CVaR的汇率风险测度

本文分别计算不同模型(GARCH模型、TGARCH模型、EGARCH模型)不同分布(正态分布、t分布、GED分布)假定下，人民币汇率波动风险的CVaR值和VaR值，通过对结果的对比分析，以期解决如下问题:

(1)不同的GARCH模型对CVaR和VaR计算结果的影响;

(2)不同的分布假定对CVaR和VaR计算结果的影响;

(3)不同的置信水平对CVaR和VaR计算结果的影响.

2.1 样本的选择及数据基本分析

本文选取2005年7月25日至2009年6月29日人民币兑美元的名义汇率日数据，共961个观察值，数据来源于外汇管理局网站.汇率收益率采用自然对数收益率形式，即:rt=lnpt－ lnpt－1，其中，pt为第t日的汇率收盘价，pt－1为第t－1日的汇率收盘价.对序列rt的统计特征进行分析，具体结果见表1～表3.

表1 基本统计特征表Tab.1 Basic characteristics of statistics

由表1的结果可知:偏度为－0.602127，表明序列rt的分布是向左偏斜的，JB统计量非常显著，因此拒绝正态分布的原假设，表明序列rt不服从正态分布;峰度为5.696138，大于3，表明序列rt具有尖峰厚尾特征.

表2 平稳性检验结果Tab.2 Inspection results of stationarity

由表2的结果可知:在1%的显著性水平下，人民币汇率收益率序列通过ADF检验，也即在样本期内，人民币汇率收益率序列为平稳时间序列.

表3 异方差检验结果Tab.3 Inspection results of heteroscedasticity

表3中，Obs*R-squared为LM统计量，其概率为0，故可以在1%显著性水平下拒绝原假设，认为序列rt存在异方差现象.

2.2 不同分布假定下的风险测度

2.2.1 正态分布假定

在正态分布假定下，经过模型的筛选，认为GARCH(1，1)-n、TGARCH(1，1)-n和 EGARCH(1，1)-n模型拟合效果比较理想.根据估计出的GARCH(1，1)-n、TGARCH(1，1)-n和 EGARCH(1，1)-n模型可以得到人民币/美元名义汇率收益率序列在正态分布假定下的各条件标准差序列，将其分别代入VaR计算公式(3)和正态分布假定下CVaR计算公式(5)，可以计算得到在正态分布假定下，不同GARCH模型在不同置信水平下的日CVaR值和日VaR值，限于篇幅，本文不列举所有的CVaR和VaR结果，只给出各CVaR和VaR序列的一般统计特征以及用返回检验得到的失败天数和失败率，具体结果见表4.

从表4的结果来看，在正态分布假定下，同一置信水平下3种模型计算得到的VaR和CVaR均值无明显差别，EGARCH-n模型的VaR和CVaR标准差要小于GARCH-n和TGARCH-n模型，3种模型估计的失败天数相差不明显，失败率均小于相应的失败期望概率.

2.2.2t分布假定

在t分布假定下，经过模型的筛选，认为GARCH(1，1)-t、TGARCH(1，1)-t和 EGARCH(1，1)-t模型拟合效果比较理想.根据估计出的GARCH(1，1)-t，TGARCH(1，1)-t和 EGARCH(1，1)-t模型可以得到人民币/美元名义汇率收益率序列在t分布假定下的各条件标准差序列，将其分别代入VaR计算公式(3)和t分布假定下CVaR计算公式(6)，可以计算得到在t分布假定下，不同GARCH模型在不同置信水平下的日CVaR值和日VaR值，限于篇幅，本文不列举所有的CVaR和VaR结果，只给出各CVaR和VaR序列的一般统计特征以及用返回检验得到的失败天数和失败率，具体结果见表5.

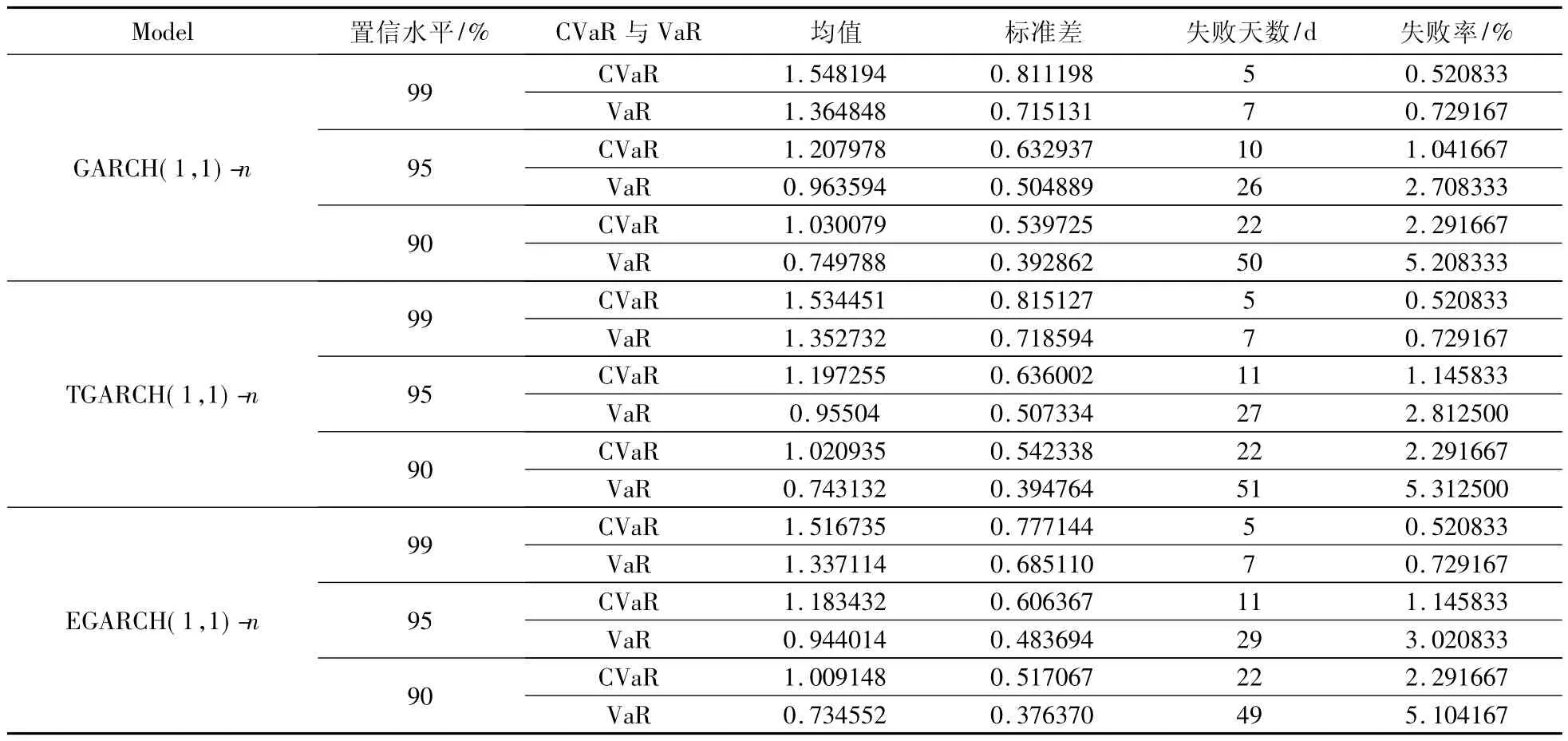
表4 基于正态分布假定的CVaR值和VaR值估计结果Tab.4 Results of CVaR and VaR under normal distribution assumptions

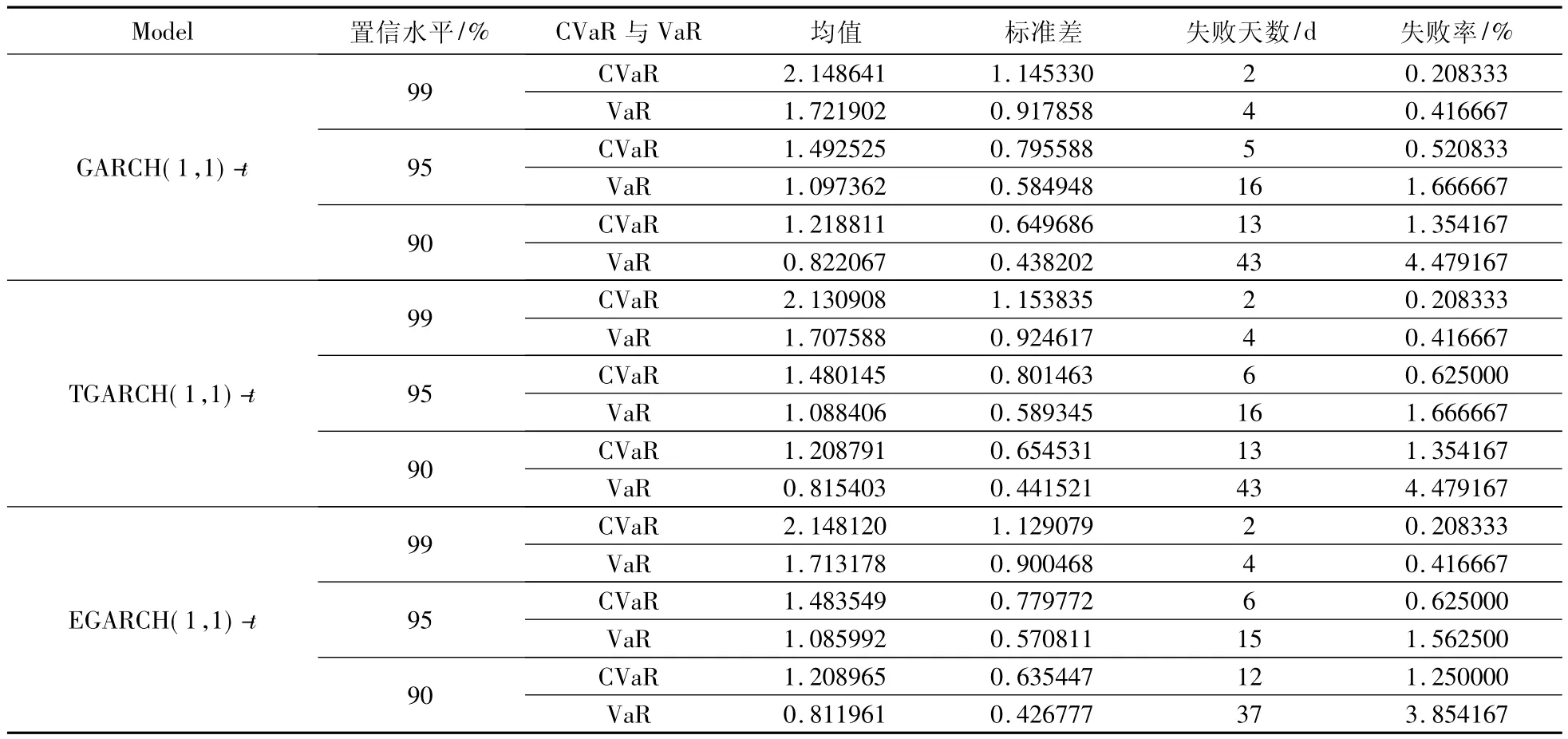
表5 基于t分布假定的CVaR值和VaR值估计结果Tab.5 Results of CVaR and VaR under t distribution assumptions

从表5的结果来看，在t分布假定下，同一置信水平下3种模型计算得到的CVaR和VaR的均值及标准差均无明显差别，3种模型估计的失败天数相差不明显，失败率均小于相应的失败期望概率.

2.2.3 GED 分布假定

在GED分布假定下，经过模型的筛选，认为GARCH(1，1)-GED、TGARCH(1，1)-GED 和EGARCH(1，1)-GED模型拟合效果比较理想.根据估计出的 GARCH(1，1)-GED，TGARCH(1，1)-GED和EGARCH(1，1)-GED模型可以得到人民币/美元名义汇率收益率序列在GED分布假定下的各条件标准差序列，将其分别代入VaR计算公式(3)和GED分布假定下CVaR计算公式(7)，可以计算得到在GED分布假定下，不同GARCH模型在不同置信水平下的日CVaR值和日VaR值，限于篇幅，本文不列举所有的 CVaR和 VaR结果，只给出各CVaR和VaR序列的一般统计特征以及用返回检验得到的失败天数和失败率，具体结果见表6.

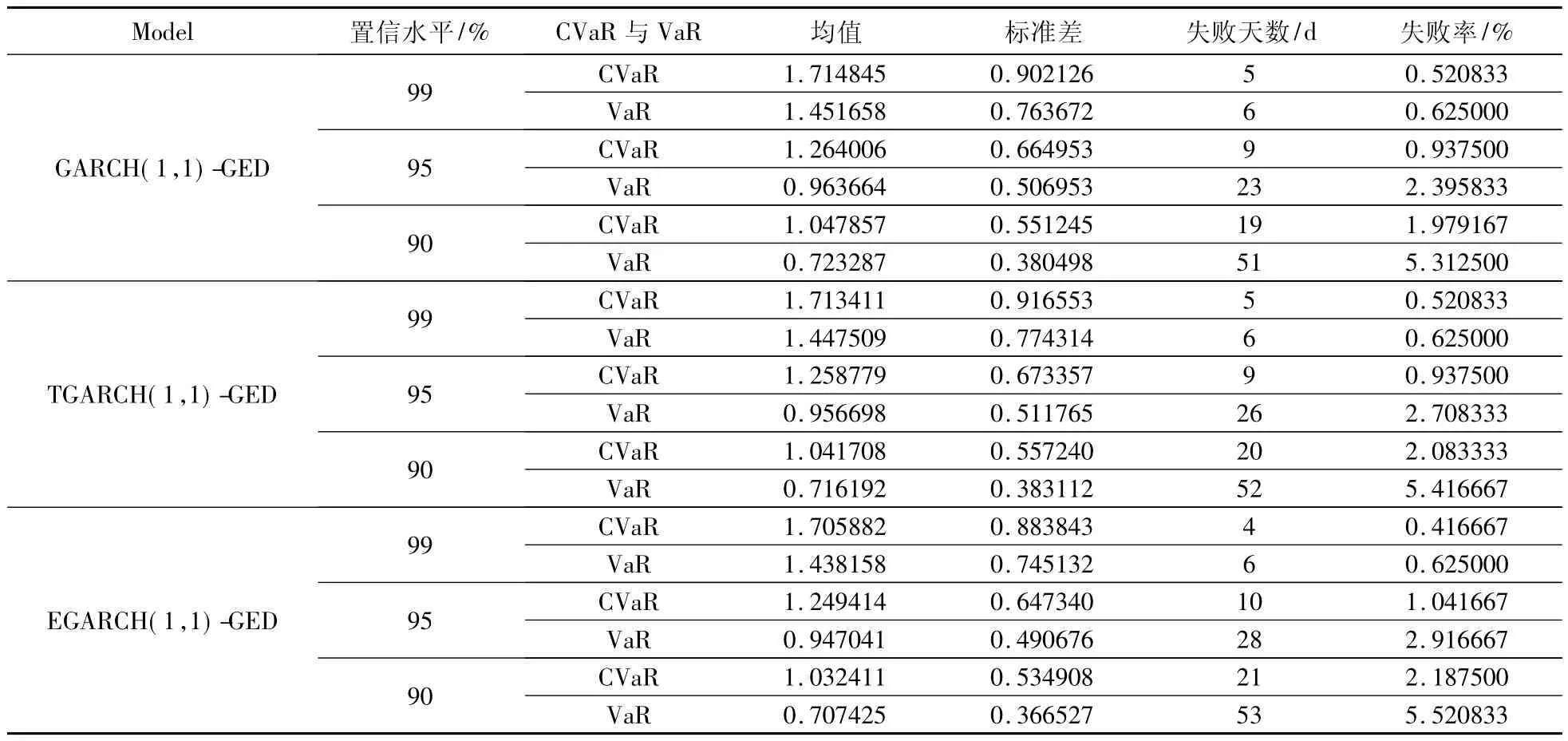
表6 基于GED分布假定的CVaR值和VaR值估计结果Tab.6 Results of CVaR and VaR under GED distribution assumptions

从表6的结果来看，在GED分布假定下，同一置信水平下3种模型计算得到的CVaR和VaR均值均无明显差别，3种模型估计的失败天数相差不明显，失败率均小于相应的失败期望概率.

2.2.4 风险测度结果分析

通过前面的风险测度结果，可以得到以下结论:

(1)在相同的分布假定下，GARCH模型的种类对CVaR和VaR的计算结果影响不明显.从上述的实证结果可见，在同一分布假定下，通过GARCH，TGARCH和EGARCH模型计算的CVaR和VaR的均值、标准差和失败天数等指标均无显著差异，这表明尽管TGARCH和EGARCH模型可以更好地描述汇率收益率序列的非对称效应，但模型的改进对CVaR和VaR的影响不是很显著.

(2)在相同的GARCH模型下，不同的分布假定对CVaR和VaR的计算结果影响显著.从上述的实证结果可见，在同一GARCH模型和相同的置信水平下，t分布假定下估算的CVaR和VaR失败天数均小于正态分布和GED分布下估算的CVaR和VaR失败天数，这表明t分布更准确地描述了汇率收益率序列的厚尾特征，其估算的CVaR和VaR对实际损益的覆盖程度更高.

(3)在相同分布、相同GARCH模型下，不同的置信水平对CVaR和VaR的计算结果影响显著.从上述的实证结果可见，在同一分布和GARCH模型下，置信水平越高，估算的CVaR和VaR失败天数越小，CVaR和VaR结果对实际损益的覆盖程度越高，因此，置信水平的选择对CVaR和VaR的计算有显著的影响.

3 CVaR与VaR的对比研究

3.1 CVaR与VaR风险测度效果比较

为了比较CVaR与VaR对汇率风险的测度效果，先将表4～表6中99%置信水平下各分布的数值汇总成如下表7，再进行对比分析.

从表7的比较结果可见，在99%置信水平下，基于相同的分布假定和GARCH模型，CVaR的均值大于相应的VaR估计的均值;从失败天数和失败率来看，CVaR的失败天数和失败率均小于相应的VaR的失败天数和失败率，尤其是t分布假定下，3种模型的失败天数减少了50%，这表明相对于VaR而言，CVaR是一种能覆盖更大范围尾部风险的风险测度指标.

95%、90%置信水平下对CVaR与VaR的比较，类似于表7，因篇幅有限表格不再列出，具体数据参见表4～表6，此处只作结果分析.在95%置信水平下，基于相同的分布假定和GARCH模型，CVaR的均值大于相应的VaR估计的均值;从失败天数和失败率来看，CVaR的失败天数和失败率均小于相应的VaR的失败天数和失败率，其中t分布假定下，3种模型失败天数的减少力度最大，减幅近69%，GED分布和正态分布假定下，3种模型失败天数的减幅分别在65%和60%左右，这表明相对于VaR而言，CVaR是一种能覆盖更大范围尾部风险的风险测度指标.

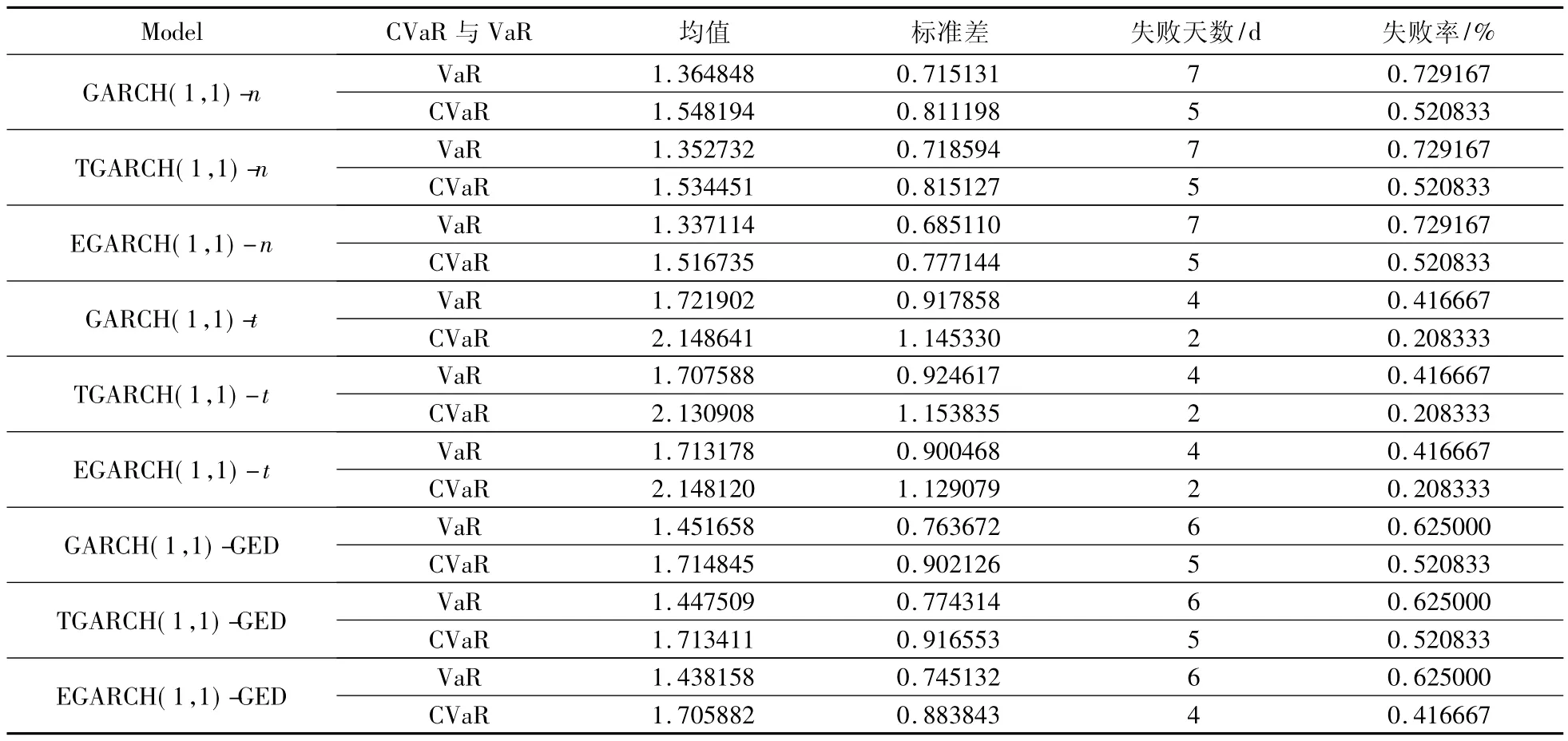
表7 99%置信水平下CVaR与VaR的比较Tab.7 Comparative results between CVaR and VaR under 99%confidence level

90%置信水平下，基于相同的分布假定和GARCH模型，CVaR的均值大于相应的VaR估计的均值;从失败天数和失败率来看，CVaR的失败天数和失败率均小于相应的VaR的失败天数和失败率，其中t分布假定下，3种模型失败天数的减少力度最大，减幅在68%左右，GED分布和正态分布假定下，3种模型失败天数的减幅分别在61%和55%左右，这表明相对于VaR而言，CVaR是一种能覆盖更大范围尾部风险的风险测度指标.

3.2 CVaR和VaR对比结果分析

通过前文CVaR和VaR的风险测度对比结果，可以得到以下结论:

(1)分布假定显著影响CVaR对VaR的改进效果.3种置信水平下，均是t分布假定下各模型失败天数的减少力度最大，这表明t分布能更准确地描述汇率收益率序列的变化特征，其估算的CVaR结果对VaR结果的改进效果更显著.

(2)置信水平显著影响CVaR对VaR的改进效果.95%和90%置信水平下，各模型失败天数的减少力度较大，减幅均高达60%以上，而99%置信水平下，各模型失败天数的减幅相对较小，导致这一现象的原因是:在99%置信水平下，仅有1%的尾部风险被VaR忽略，此时，VaR值对实际损失的覆盖程度已经较高，失败率也已较低，进而使得该置信水平下CVaR对VaR的改进效果不明显.

［1］Artzner P，Delbaen F，Eber JH，et al.Coherentmeasure of risk［J］.Mathematical Finance，1999(3):203-228.

［2］Acerbi C，Tasche D.On the coherence of expected shortfall［J］.Journal of Banking and Finance，2002，26(4):1491-1507.

［3］徐绪松，杨小青，陈彦斌.半绝对离差证券组合投资模型［J］.武汉大学学报:理学版，2002(3):297-300.

［4］李仲飞，汪寿阳.EaR风险度量与动态投资决策［J］.数量经济与技术经济研究，2003(1):45-51.

［5］Rockafeller T，Uryasev S.Optimization of conditional value-at-risk［J］.Journal of Risk，2000，2(3):21-42.

［6］周小敏.基于GARCH模型的CVaR金融风险测度研究［D］.长沙:湖南大学硕士学位论文，2007:32.