基于债券久期思想对投资回收期法的改进
林清泉,李锦涵
(1中国人民大学中国财政金融政策研究中心,北京100872;2中国人民大学财政金融学院,北京100872;3中国人民银行上海总部,上海200120)
1 研究背景
投资回收期法(payback period method)是项目投资决策中广泛采用的资本预算方法,具有使用简单方便的优点.Klammer(1972)[1]发现,在大公司中回收期法虽然使用率从1959年的34%下降到1970年的26%,但仍然占据投资决策方法中很大的比重.Stanley和 Block(1984)[2]通过对美国大型跨国公司的问卷调查发现:回收期法虽然很少被作为首选的决策方法,但在辅助方法中使用率却是最高的;另外,对美国公司的一些调查发现:在公司首席财务官对资本预算方法的选择中,回收期法占到了56.7%,使用回收期法在小公司中就更为普遍.以上的这些研究都表明回收期法在实务中的重要性.
回收期法和其它投资决策方法相比,有其独特之处.因为净现值法、内部收益率法、平均会计收益率法、获利指数法等都是从金额和收益率的角度对投资项目进行分析的,只有投资回收期法是从时间,即项目见效快慢的角度对投资项目进行分析的,所以具有其它方法不可替代的作用;但另一方面,投资回收期法也存在着较多不足之处,比如没有考虑货币的时间价值(尤其是在项目要求的回报率较高时),没有考虑现金流量在时间上的分布,没有考虑回收期后的现金流量(尤其是当项目回收期后有较大金额的现金流入或流出时)等缺点,所以回收期法在使用中,不断有人提出修正方法.
比如为了考虑货币的时间价值,有人提出了折现回收期法,即先对各期的现金流量进行折现,再利用各期折现后的金额求出达到初始投资所需要的时间长短.但折现回收期法只是在回收期法和净现值法之间取的一种折衷的方法,一方面它没有考虑现金流量在时间上的分布,比如表1所示的A、B、C 3个备选投资方案的决策问题.

表1 A、B、C 3个项目的折现回收期评价Tab.1 Discount payback period assessment of investment projects A,B and C
如果采用折现回收期法,则3个项目方案不存在差别,但从现金流的时间分布可以看出,C方案的现金在3个时期均匀分布,第1期和第2期的现金流量高于其它方案,投资回收主要在前面两期,投资回收快;而A方案的现金流全部集中在第3期,这表明该方案投资回收慢.显然折现回收期无法考虑这种差别;另一方面,和回收期法一样,折现回收期也只考虑了投资回收期以前的现金流量,而没有考虑后续的现金流入、流出的可能性.
又如为了考虑货币时间价值和有多期投资支出的情况,有人提出了动态回收期法,即将各期的现金流入量减去现金流出量得到各期现金净流量,然后对各期现金净流量折现后进行累加,直到累加值为0,从而求出动态回收期.但动态回收期也存在没有考虑回收期以后现金流量的缺陷,使得投资决策带有急功近利的特点.
我国学者和实务界人士曾提出了一些改进回收期法的措施,安劲松(1995)[3]提出投资回收期在使用时应考虑所得税的影响.陈珠明(2001)[4]提出市场机制下回收期的计算方法.冯军(2002)[5]认为回收期法应考虑固定资产折旧、税金和流动资金投资等因素.邵希娟和杜丽萍(2007)[6]就回收期法的适用性问题也进行了探讨.但上述改进措施主要是在方法的使用上增加实务中应该考虑的税收、折旧、流动性等因素,且改进措施的入手点只是从现金流金额的角度分析的,未能解决回收期法的上述不足,没有克服该方法未考虑现金流量在时间上的分布及回收期后的现金流量的缺陷.金峻炎等(2010)[7]提出将加权马氏链用于房地产项目投资回收期的预测中,但引入加权马氏链也没有克服投资回收期法本身的缺陷.
李冠众、陆宇建和孙卫业(2001)[8]曾提出综合考虑货币的时间价值和现金流在时间上分布来改进回收期法的设想,该方法在一定程度上解决了如表1所示的现金流分布差异的问题,但该方法的使用有2个隐含的前提,即各方案初始投资支出相同且投资支出只发生一次,但现实中要比较的投资方案往往初始投资额是不同的,而且很多投资支出是分期进行的.
本文研究的是如何从投资回收期本身即考虑时间参数的影响,来改进投资回收期法.借助衡量债券现金流量时间长短的久期概念,构造解决回收期法未考虑货币时间价值、现金流分布的时间差异及回收期后的现金流入和流出情况的缺陷,同时保留投资回收期从时间长短角度来评价投资项目优劣特点的模型.
2 调整后的回收期模型
2.1 债券的久期
债券久期的概念由Macaulay(1938)[9]提出,也被称为Macaulay久期,主要用于固定收益证券的定量分析和近似计算.设某一债券能带来一系列的现金流:C0,C1,C2,…,Cn,并且各期现金流对应的时间为距现在T0,T1,T2,…,Tn.
当利率期限结构是平坦的时,也就是说对于不同时间的现金流,它们折现时使用的零息利率是相等的都为r(年度百分率形式),并且利率按连续复利计息(在连续复利情况下,1元钱的存款以年度百分率r计息,1年后的本利之和为er,那么,据今天1年的1元钱的现值为e-r,同理,距今天T(T可以取任意实数)年的1元钱的现值为e-rT).
用折现现金流法则,上述债券的理论价格为B定义债券的久期为D=实际上债券的久期是各期现金流时间Ti的加权平均值,权重Wi为该现金流的现值与债券价格之比,即
当利率期限结构不是平坦的时,债券的理论价格B、债券的久期D和各期现金流时间的权重Wi分别为和
特别地,不论利率期限结构是否平坦,对于到期一次还本付息债券或者纯贴现债券,可得其久期D值为T(T为距今到期的时间).
债券的久期用于度量债券现金流回收时间的长短,久期越长,回收的时间越长.
2.2 债券久期在投资决策中的应用
将投资项目视为“债券”,将项目的初始投资视为购买债券的成本,将项目产生的各期现金流入视为债券各期的利息和本金收入,则项目的回收时间可以视为“债券”的久期.
投资决策中的现金流毕竟和债券定价中的现金流不同,前者可能需要分期投资,每期既有可能现金流入,也有可能现金流出;后者初始时期一次性支付债券的成本之后,每期只有现金的流入,久期只研究初始购买债券以后的各期现金流入.
在投资带来的各期现金流入量完全相同并且初始投资额也相同的情况下,需要后续投资的项目比不需要后续投资的项目的回收期要长,相应的需要后续投资的项目投资支出现值之和比不需要后续投资的项目投资支出现值要大,这就为分期投资项目的投资回收期长短的计算提供了思路.
在同一时点既有现金流入又有现金流出时,首先应该计算现金的净流量是流入的还是流出的,如果是净流出量,视为只有现金流出,如果是净流入量,视为只有现金流入(因为某一期现金流入100单位同时现金流出50单位与某一期只有现金流入50单位在计算时是没有区别的,都视为该时刻只有现金流入50单位).
2.3 模型的建立
记各期的现金流入量(指净流入量)为I1,I2,…,In且互不相关,对应的时间为T1,T2,…,Tn,现金流出量(指净流出量)为O1,O2,…,Om且互不相关,对应的时间为t1,t2,…,tm(t1,t2,…,tm和T1,T2,…,Tn是不同的,因为如果同一时刻既有现金流出又有现金流入,只需计算净现金流量即可).
当利率的期限结构不平坦时,各期现金流出量的现值之和O、各期现金流入量的现值之和I和项目现金流入量的久期D分别为表示回收1单位的现值所需要的久期的长短,F越大,表明相对于一定的收益现值I而言,久期D越长,表明回收期越长,反之,表明回收期越短.
由于项目的回收期取决于F和项目的各期投资支出的现值O,F可以理解为回收1单位现值所需要的久期,那么F和各期投资支出的现值O的乘积很自然地可以理解为回收全部投资支出现值所需要的久期,即回收期.定义“调整后的回收期”为S=F×O.
该调整后的回收期S既考虑了项目各期现金的流入、流出,也考虑了货币的时间价值.
3 模型分析
3.1 调整后的久期与获利指数的关系
3.2 调整后的久期与各期现金流出量的现值之和O的关系
在各期现金流入量不变(I和D不变,单位现值的久期因子F也不变)的情况下,各期现金流出量的现值之和O增加,调整后的久期也增加,表明各期投资支出现值增加,项目回收投资的速度越慢.
3.3 调整后的久期与各期现金流入量时间的关系
在各期现金流出量现值之和O不变的情况下,由于当某一期现金流入量Ij对应的时间Tj提前时,由于久期D会减小,而各期现金流入量现值之和I增加,所以单位现值的久期因子F减少,调整后的久期S减小,表明某一期现金流入量Ij对应的时间Tj提前(Tj减小)时,项目资金回收速度变快.
3.4 调整后的久期与各期现金流入量大小的关系
在各期现金流出量现值之和O不变、各期现金流入量的时间T0,T1,T2,…,Tn不变和其它期现金流入量大小不变的情况下,某一期现金流入量Ij的变化对调整后久期的影响可以通过Ij的变化对单位现值的久期因子F的影响来研究:
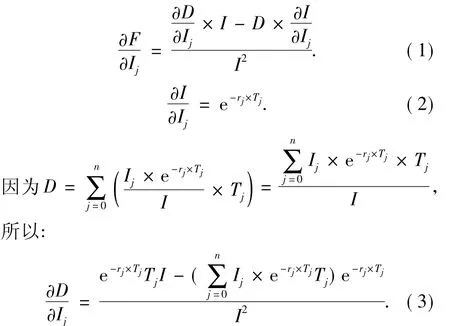
将(2)、(3)式代入(1)式得:
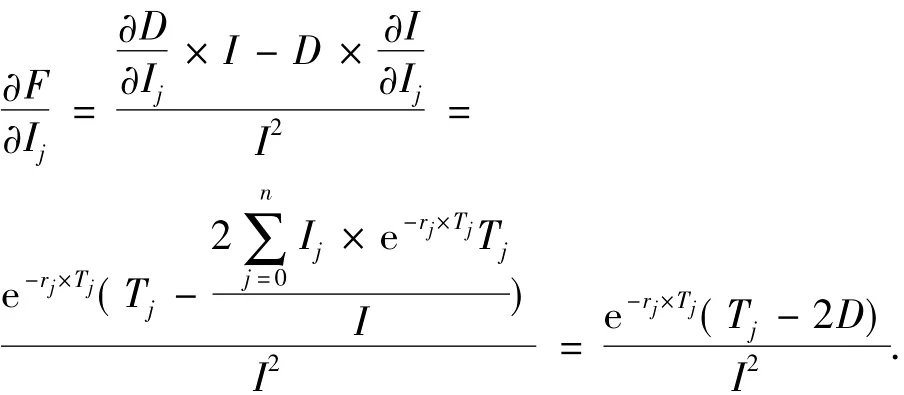
(1)当Tj>2D时表明当较远期(“终期”后)的现金流入量Ij增加时,久期D增加的比例大于总的净现值I增加的比例,单位净现值的久期因子F增大,调整后的回收期S增大.因为此时整个现金流入量的分布集中于“终期”后的程度增加(因为D为现金流入时间的加权平均值,可以视为现金流入时间的“中点”,则2D可以视为现金流入的“终期”),项目的资金回收变慢.
(2)当Tj=2D时,表明当“终期”的现金流入量Ij增加时,久期D的增加同比例于总的净现值I的增加,单位净现值的久期因子F不变,调整后的回收期S不变,项目的资金回收速度不变.
(3)当Tj<2D时,表明当较近期(“终期”前)的现金流入量Ij增加时,久期D增加的比例小于总的净现值I增加的比例,单位净现值的久期因子F减小,调整后的回收期S减小,项目的资金回收变快.
4 实证分析
4.1 模型的适用性分析
下面分析折现回收期相同但各期现金流分布不同时模型的适用性.
例1 以表1提到的A、B、C 3个投资项目的比较为例,为了说明方便,10% 年折现率相当于连续复利为每年 9.53%,即 e0.0953=1+10%,分别计算上述3个项目调整后的回收期.
A方案:
各期现金流出量的现值之和OA=3000(万元),各期现金流入量的现值之和
调整后的回收期SA=FA×OA=3(年).
同理可得到B方案SB=2.5(年),C方案SC=2(年).
通过计算调整后的回收期满足SA>SB>SC.
这表明调整后的回收期模型能考虑到现金流分布不同的影响.
4.2 基于未来现金流的模型的适用性分析
下面分析投资回收期相同但投资回收期后还有现金流入流出时模型的适用性.
例2对表2所示的A和B两个项目作比较.

表2 A和B两个项目的折现回收期评价Tab.2 Discount payback period assessment of investment projects A and B
为了说明方便,假设年折现率为10%,相当于连续复利为每年9.53%,即 e0.0953=1+10%,分别计算调整后的回收期.
A方案:
各期现金流出量的现值之和OA=100(万元),
调整后的回收期SA=FA×OA=1.91(年).
同理可得到B方案SB=0.00974(年).
通过计算,调整后的回收期满足SA>SB.
这表明,对于投资回收期法无法反映的项目回收期后现金流量的差异,调整后的回收期很好地考虑了.
5 结语
投资回收期法是在投资决策中广泛采用的资本预算方法,该方法从项目投资回收快慢和回收时间长短的角度来评价投资项目,但存在没有考虑货币时间价值,没有考虑现金流量时间分布的差异,没有考虑回收期以后的现金流量等缺陷.本文用债券久期的观点,将项目的现金流量和债券的现金流量进行类比,建立了克服传统回收期法上述缺陷的“调整后的回收期”模型,以便于投资决策实际运用.
[1]Klammer T.Empirical evidence of the adoption of sophisticated capital budgeting techniques[J].The Journal of Business,1972,7:387-397.
[2]Stanley M T,Block SB.A survey ofmultinational capital budgeting[J].The Finance Review,1984,3:36-51.
[3]安劲松.对投资回收期计算方法的改进意见[J].上海会计,2006(12):20-21.
[4]陈珠明.投资回收期研究[J].工业工程,2001,4(1):41-44.
[5]冯 军.投资回收期指标若干问题的探讨[J].北方经贸,2002(2):56-57.
[6]邵希娟,杜丽萍.关于投资回收期法的探讨[J].财会通讯:理财版,2007(1):29-30.
[7]金峻炎,陈 进.加权马氏链在房地产投资回收期预测中的应用[J].湖南科技大学学报:自然科学版,2010,25(2):63-66.
[8]李冠众,陆宇建,孙卫业.投资回收期法的评价与模型修正[J].经济问题探索,2001(8):71-73.
[9]Macaulay F R.Some theoretical problems suggested by themovements of interest rates,bond yields,and stock prices in the United States since 1856[M].New York:Columbia University Press,1938:44.

