基于LBP和PCA特征提取的人脸识别

熊承义，李丹婷，笪邦友

(中南民族大学电子信息工程学院，武汉430074)

人脸识别是生物特征识别领域甚至人工智能领域最困难的研究课题之一，它涉及模式识别、图像处理、计算机视觉、生理学、心理学等诸多学科的知识背景.其中，人脸表达是一个关键步骤，其有效性与识别结果密切相关.目前，人脸识别的研究重点逐渐集中于人脸表达，其研究具有较强的现实意义及相当的实用价值.

人脸表达的实质即为特征提取.数10年以来，基于全局特征提取的子空间方法取得了巨大的成功，主要包括主成分分析(PCA)、线性鉴别分析(LDA)、独立分量分析(ICA)等 .Kirby［1］和 Turk［2］等人提出的PCA方法通过线性变换找到在最小均方意义下最能代表原始人脸图像的正交基，使得图像数据从高维空间压缩到低维空间，不仅得到了原始数据的紧致表达，而且大大降低了计算复杂度.Belhumeur［3］等人提出的Fisher LDA以样本可分性为目标使得样本类间离散度与类内离散度比值最大，但在小样本情况下不足以描述人脸变化.Bartlett［4］等人提出的ICA方法是基于所有阶统计意义下的去相关，它的计算复杂度要高于PCA，且在识别率上没有优势.不仅如此，基于全局特征的人脸表达对于光照、姿态、表情等因素的影响较为敏感.

相对来说，基于局部特征的人脸表达对于光照、姿态的变化更为鲁棒，1997年，Wiskott等人提出的弹性图匹配(EBGM)算法［5］，他们用一组描述人脸局部特征的Gabor小波变换系数对人脸图像各部分进行最佳匹配，但它对特征点的选择和配准有较高要求，且计算复杂.2004年，Ahonen等人提出基于LBP特征的人脸表达方法［6，7］，在FERET人脸库上得到了最好的识别结果.2008年，Zhao等人提出的将LBP和Gabor相结合的算法在表情识别上取得了相对于其他算法较好的效果［8］.Tang等人提出的Haar LBP算法在姿态、表情、光照变化上取得了不错的结果［9］.但其得到的人脸表达往往具有较高的维数，直接影响了识别速度.

为能有效地降低计算复杂度，本文在分析局部二元模式在人脸表达具有优势的基础上，通过利用主成分分析能够降低人脸特征维数的特点，提出了将主成分分析与局部二元模式相结合的方法.该方法首先对人脸图像进行分块，然后对分块后的人脸图像进行直方图特征向量提取，再对直方图特征向量进行降维处理.实验结果表明，该方法保留了LBP特征的良好特性，同时又有效地降低了计算复杂度.

1 基于局部二元模式的人脸表达

LBP算子的基本思想是将中心像素点的灰度值设为阈值，其圆形邻域内的像素点与之作比较得到二进制码用来表述局部纹理特征.它计算简单，分类能力强，在描述纹理特征提取方面有着显著的效果.LBP算子通常由参数(P，R)来表示，其中P表示邻域内包含的像素个数，R表示邻域半径.对于不同的(P，R)值对，LBP算子也不相同，图1为3种不同的LBP算子.

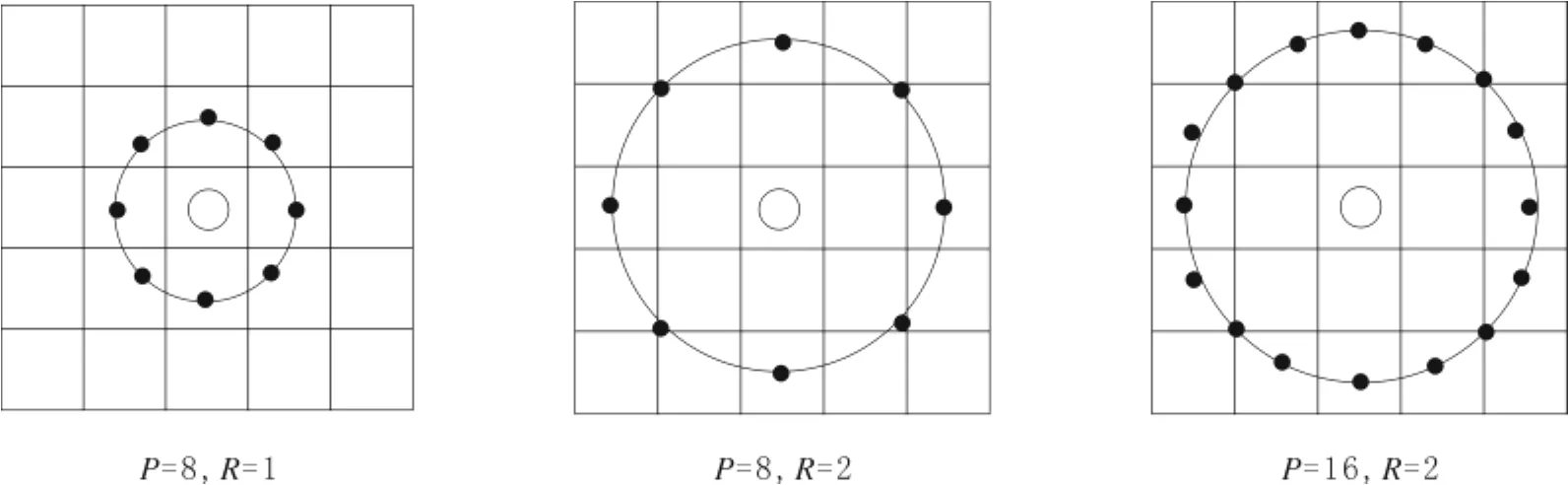
图1 不同P、R值对应的LBP算子Fig.1 Circularly symmetric neighbor sets for different(P，R)

对于任意的LBP算子，它的编码公式为:

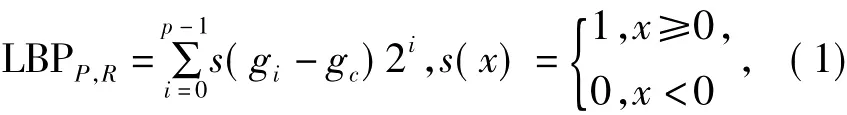
式中，gi(i=0，…，P－1)表示P个以中心像素gc为圆心，R为半径的圆周上的像素值.具体的LBP算子计算过程如图2所示.将图2左边模板阈值化，使各邻域像素点与中心像素作比较，大于0置1，小于0置0，得到图2中图，确定各像素点的权重，得到图2右图，则LBP算子即为阈值化后各像素与对应权重的点积.

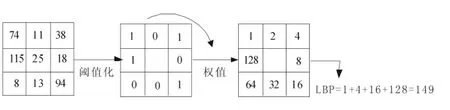
图2 基本LBP算子Fig.2 Basic LBP operator

人脸图像经过LBP算子运算后，对其做直方图统计，得到直方图特征向量.可定义为:

将原始图像fl(x，y)划分成区域R0，R1，Rm－1，对分块后的子图像进行LBP直方图统计，各分块子图像直方图表达式为:

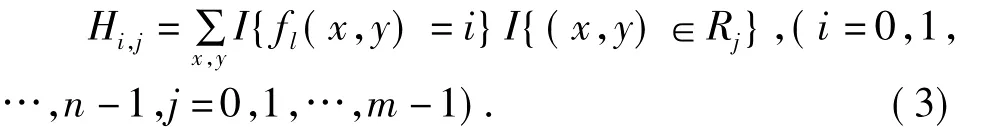
然后将这些子区域直方图连接起来构成人脸特征向量，并对直方图特征向量进行统一模式转换.图3为LBP直方图人脸表达示意图.本文利用χ2统计量来度量两个LBP特征之间的距离，用(4)式计算:

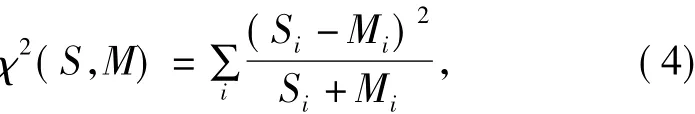
其中S、M分别为两个直方图特征向量.

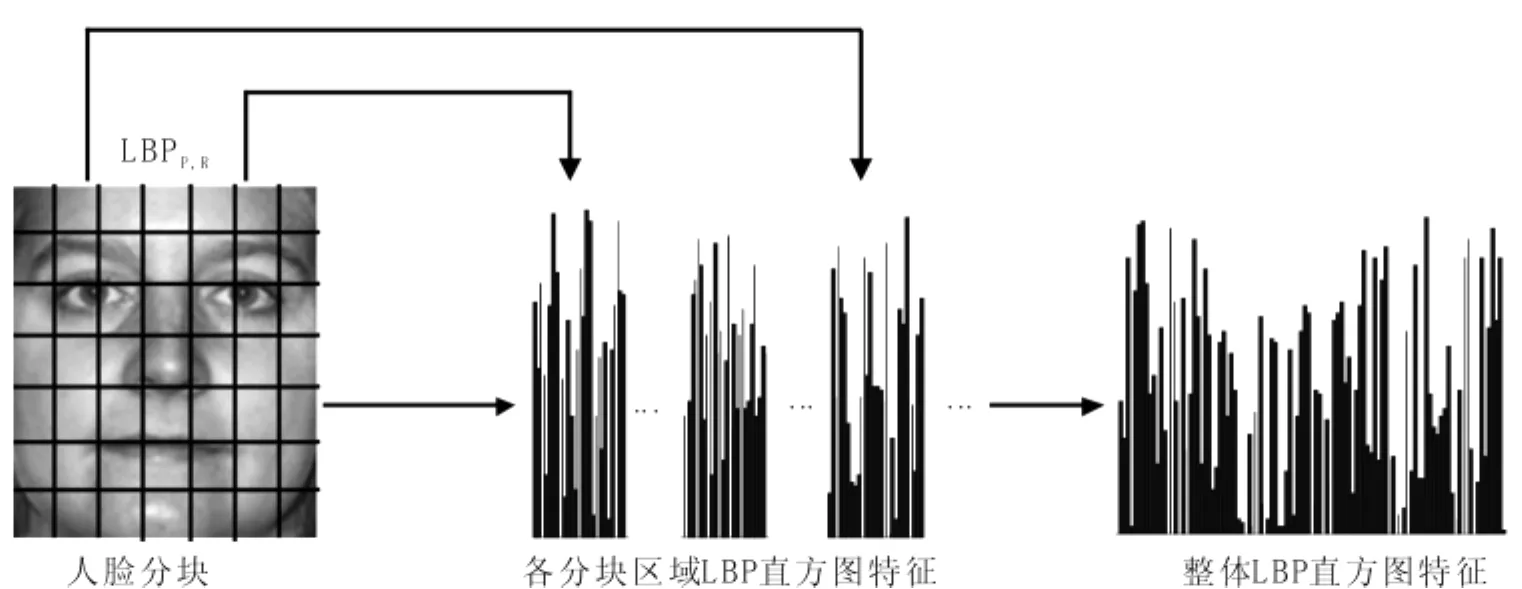
图3 基于LBP的人脸表达Fig.3 Face expression based on LBP

2 主成分分析

基于主成分分析(PCA)的人脸识别方法最初由Kirby提出［1］，Turk后来把它成功地发展为特征脸(Eigenface)方法［2］，该方法的基本思想来源于K-L变换，其通过将人脸作为一个整体处理，利用线性变换提取其中的主元，而去除其次要的分量，最后构成特征脸空间.识别时将测试图像投影到此空间，得到一组投影系数，用于表达人脸.主成分分析最显著的优点在于通过降低特征维数，使得特征表达更为紧凑，利于分类，并降低计算强度.

假设训练图像有N幅，图像大小为m×n，图像维数为M=m×n，将第i幅训练图像转化为一维的列向量xi，则N幅训练样本集为:

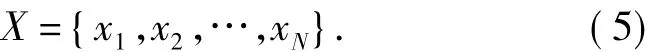
训练集的样本均值为:

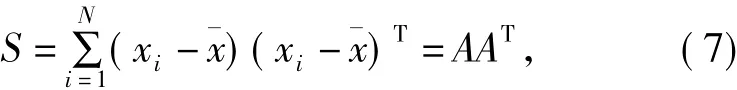
显然，协方差矩阵S为实对称矩阵，大小为M×M.

PCA提取的主元方向即为协方差矩阵S的特征向量.因协方差矩阵S为实对称矩阵，其特征值均为实数，将其M个特征值按大小进行排序，即λ1≥λ2≥…≥λM，则前m个最大特征值对应的特征向量即为所需的主元方向.

3 结合PCA的LBP特征降维

基于LBP和PCA的人脸识别过程如图4所示，本文工作主要集中在特征提取阶段.主要包括以下步骤:(1)在提取LBP描述子前，对原始图像进行分块;(2)计算各分块LBP描述子，统计分块图像的LBP直方图，并将每个子图像LBP直方图特征连接成一维向量;(3)采用PCA方法对LBP直方图向量进行降维，最终得到人脸图像的特征表达.

图4 基于LBP和PCA的人脸识别流程图Fig.4 Flow chart of face recognition based on LBP and PCA

流程图中特征提取的3个步骤为:

Step1图像分割.

在提取LBP描述子前，选择分块方式，将图像分割成为大小相等的方块，以利用LBP进行特征提取.

Step2求取各分块的LBP直方图.

分割完图像后，对每个分块进行LBP特征向量提取，得到该分块的LBP直方图表示形式.基本思想是定义一个模板，对于各分块中除去边缘的点，使其邻域内的像素值与中心像素值进行差值比较，对不同的比较结果赋予不同的权值，变换图像中的点就为各位置比较结果的加权和.为了获得特征值的分布情况，需要对特征值矩阵进行直方图统计，将得到一个2p－1的直方图向量.

Step3对直方图向量降维.

在PCA降维阶段，对所有直方图向量求解平均向量，构建协方差矩阵，计算协方差矩阵的特征值和特征向量，将特征值由大到小排列，保留前n个特征值及其对应的特征向量.

在识别阶段，采用最近邻分类器来计算测试样本与训练样本的相似度.

4 实验分析

本文采用FERET人脸库［10］对结合算法和均匀LBP进行比较验证.目前FERET人脸库包含1199个人的14051张灰度图像，这些图像包含不同光照、不同面部表情、不同年龄、不同位置角度等，本实验仅考虑正面人脸，即位置角度为0，这些人脸图像分为5类:

标准正面fa集(1196幅)，即图库集gallery，包含1196个人的正面人脸图像，一人一张;

表情fb集(1195幅)，与fa在同条件下拍摄，不同表情的人脸图像集;

光照fc集(194幅)，不同光照条件下的人脸图像集;

年龄dup1集(722幅)，相对于gallery中的图像0～18个月后拍摄的图像;

年龄dup2集(234幅)，它是dup1子集，它所包含的图像相对于gallery中的图像超过18个月.

4.1 LBP人脸表达的最优分块方法

Ahonen在其人脸识别实验中，综合考虑识别性能与计算复杂度，选定分块方式为7×7，显然更多的分块数能有效提高识别率.本实验的目的在于测试不同分块情况下LBP特征对于人脸识别的有效性.如图5所示.

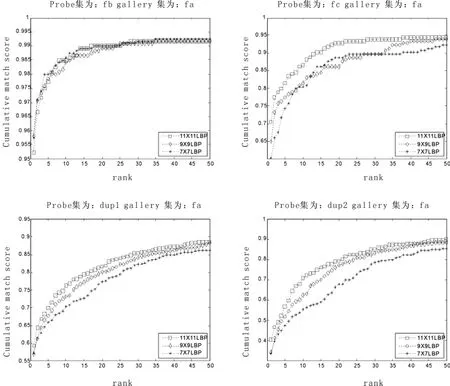
图5 不同分块数下测试集fb、fc、dup1、dup2的CMC曲线Fig 5 Rank curves for fb、fc、dup1 and dup2 probe setswith different patitions

实验结果表明，不同的分块方式在测试集fb上的识别效果基本一致，但在其它的测试集，如fc、dup1、dup2上，随着分块数的增加，识别率有较显著提高.鉴于的分块数能在各数据测试集上取得最佳的性能，本文最终选择该尺度进行进一步的实验.

4.2 结合PCA降维方法与LBP人脸表达的识别结果

通过前一个实验，将人脸图像分为个子块，对各子块提取LBP直方图后连接起来，构成人脸的特征表达，在对其分别降维到700、300后，最后采用最近邻分类器进行识别.与分块数为7×7的传统LBP方法在测试集fc、dup2上的实验比较结果如图6所示.

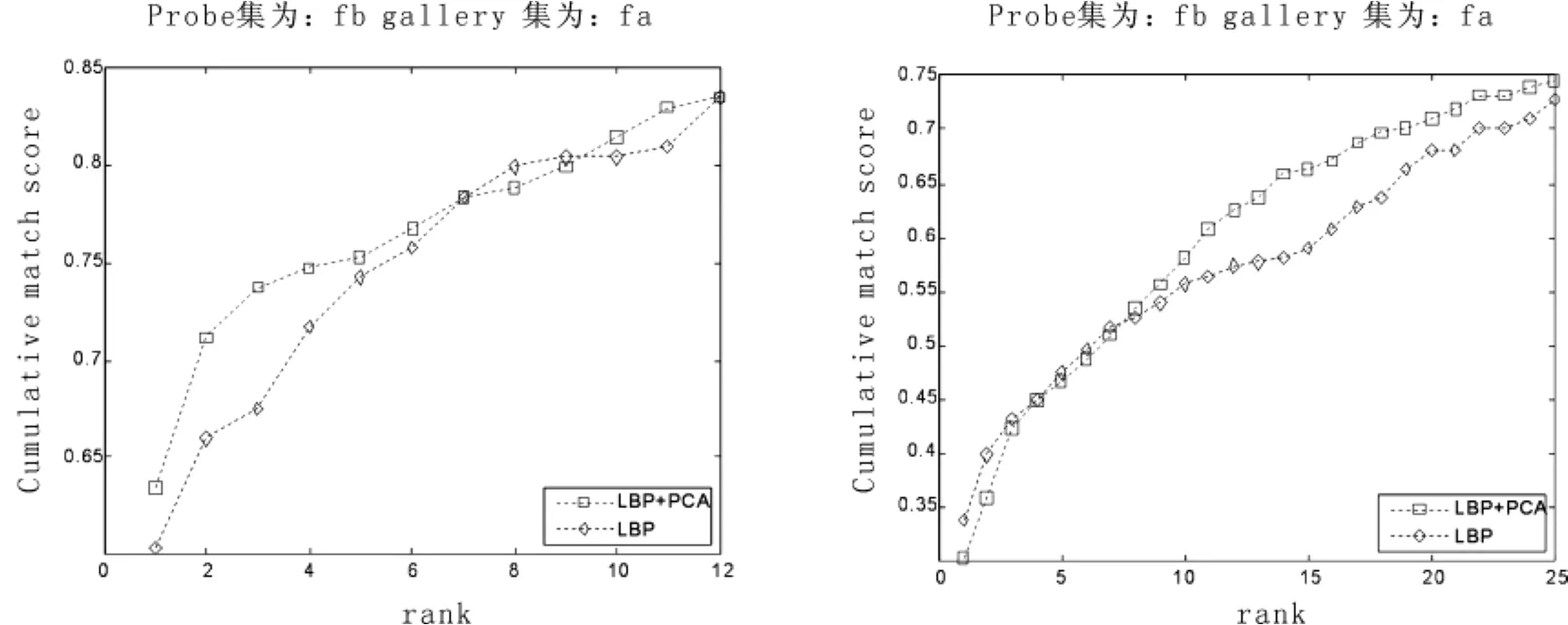
图6 两种算法在测试集fc、dup2上的CMC曲线Fig.6 Rank curves for fc and dup2 probe sets among 2 algorithms

由图6可知，在测试集fc上，分块数为11(原维数7139)降维至700的结合算法比分块数为7(原维数2891)的传统LBP算法要好，而在测试集dup2上，分块数为11降维至300的结合算法同样要比分块数为7的传统算法优越，这说明结合后的算法在光照变化集和年龄变化集上保持并有更好的识别效果.

5 结语

通过分析局部二元模式特征提取的过程，利用主成分分析低维向量表示原始数据的特点，提出了一种结合局部二元模式和主成分分析的算法.该算法与原有的局部二元模式算法相比，在保证较高的识别率的条件下，有效地降低了人脸识别阶段的计算复杂度.

［1］Kirby M，Sirovich L.Application of the Karhunen-Loeve procedure for the characterization of human faces［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12(1):103-108.

［2］Turk M，Pentland A.Eigenfaces for recognition［J］.Journal of Cognitive Neuroscience，1991，3(1):72-86.

［3］Belhumeur PN，Hespanha JP，Kriegman D J.Eigenfaces vs fisherface:recogniton using class special linear projection［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(7):711-720.

［4］Bartlett M S，Lades H M，Sejnowski T J.Independent component representations for face recognition［J］.Proceedings of SPIE，1998，3299(3):528-539.

［5］Wiskott L，Fellous JM，Malsburg C.Face recognition by elastic bunch graph matching［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(7):775-779.

［6］Ahonen T，Hadid A，Pietikainen M.Face recognition with local binary patterns［C］//ECCV.8th European Conference on Computer Vision.Prague:ECCV，2004:469-481.

［7］Ahonen T，Hadid A，Pietikainen M.Face description with local binary patterns:Application to face recognition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2006，28(12):2037-2041.

［8］Zhao Q Y，Pan BC，Pan JJ，etal.Facial expression recognition based on fusion of Gabor and LBP features［C］//ICWAPR.6th International Conference onWavelet Analysis and Pattern Recognition.Hong Kong:ICWAPR，2008:362-367.

［9］Tang H L，Sun Y F，Yin B C，et al.Face recognition based on Haar LBP histogram［J］.ICACTE，2010，6:235-238.

［10］Phillips P J，Moon H，Rizvi S，et al.The feret evaluation methodology for face recognition algorithms［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(10):1090-1104.