一类新的6维李代数及其相关的Liouville可积哈密顿系统＊

郭福奎,冯滨鲁,魏 媛,张玉峰

(1.山东科技大学,山东 青岛 266510;2.潍坊学院,山东 潍坊 261061; 3.滨州学院,山东 滨州 256600;4.中国矿业大学,江苏 徐州 221116)

1 引言

近年来可积系统理论有了迅速的发展,文献[1-4]中给出了寻求可积系统的方法。其中一种方法是著名的Lax法,它是由屠规彰教授提出的[5],后来称之为屠格式。在本文中我们将利用屠格式得到新的可积系统。因此,我们简单的介绍一下屠格式。

设G是数域C上的矩阵李代数。令G=G⊗C(λ,λ-1)是其相应的loop代数,其中 C(λ,λ-1)表示一组关于参数λ的洛朗多项式。G中基元的阶数可定义为deg(x⊗λn)=n,x∈G。

首先,记静态零曲率方程

的解为V=V(λ),且Vx(n)=(λnV)++Δn满足

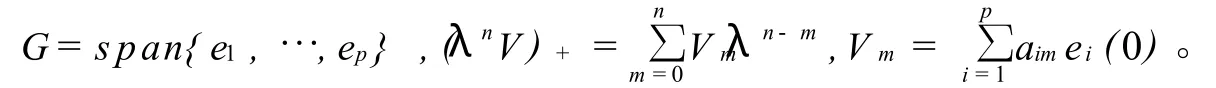
其次,利用零曲率方程

可以得到Lax可积方程族

最后,根据方程(1)我们可以得到哈密顿算子J和循环算子L,因此方程(4)可以写成哈密顿形式

其中 Hn(n∈Z)表示方程(5)的守恒密度,可以由迹恒等式[5]

计算得到,其中〈A,B〉表示矩阵的迹,例如〈A,B〉=tr(AB),∀A,B∈G。由文献[5]的论述可知,如果JL =L＊J,那么Lax可积方程族(4)是Liouville可积的。

可积系统一个重要的扩展方向是可积耦合,可积耦合是在文献[6-7]提出的,并作了相关的研究。对可积耦合的研究不仅可以帮助我们探讨可积系统的对称,还可以帮助我们发现不同进化方程的可积方程族之间的关系。例如在文献[8]中我们构造了一个可积模型(实际上是可积耦合)把著名的A KNS方程族和KN方程族联合在一起。郭福奎教授和张玉峰教授在文献[9]中提出一种简便有效地推导可积耦合的方法,其要求李代数G可以分解成两个直和子代数G1,G2它们满足

其中⊕表示直和,[,]表示李括号。自然我们会想到探讨可积耦合的一些性质,例如哈密顿结构。然而利用迹恒等式(6)是得不到哈密顿结构的。因此,我们提出一种有效的工具即二次型恒等式[10]来得到可积耦合的哈密顿结构。这个恒等式是推广的迹恒等式,也就是说迹恒等式是二次型恒等式的一种特殊的情形。为了便于阅读本文,我们先来回顾一下二次型恒等式。

其中 a,b∈G,F=(fij)s×s是常数对称矩阵。我们要求(8)满足以下关系

其中U,V满足Vx=[U,V],Λ∈G。关于W的两个约束条件为

我们可以得到

都是方程(1)的解,所以存在常数满足

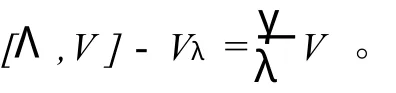
由(15)可以推导出二次型恒等式

本文中,介绍了一类新的6维李代数V6,其具有显著的特点,例如它不满足关系式(7)。因此,利用V6和屠格式所生成的可积系统不是可积耦合。下面,我们会推导出两类新的进化方程的Liouville可积方程族并根据二次型恒等式得到它们的哈密顿结构。

2 一类新的李代数和两类可积方程族

设

其中ei(i=1,2,3,4,5,6)为V6的一组基,并满足下面的换位运算

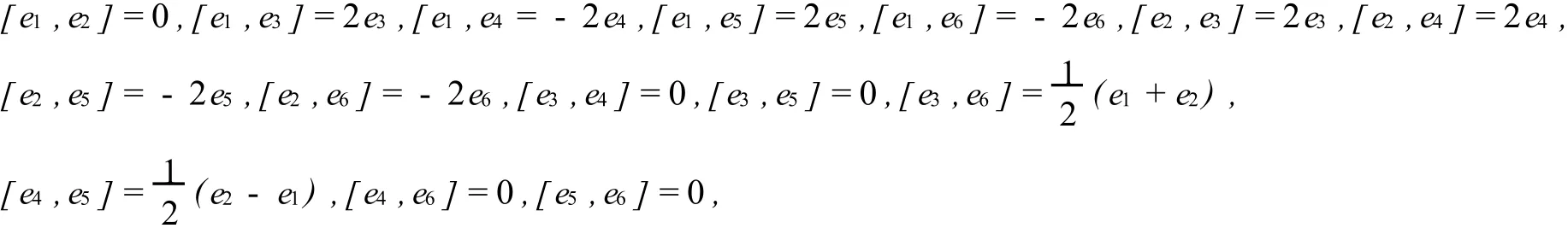
其中[a,b]=ab-ba,a,b∈V6。

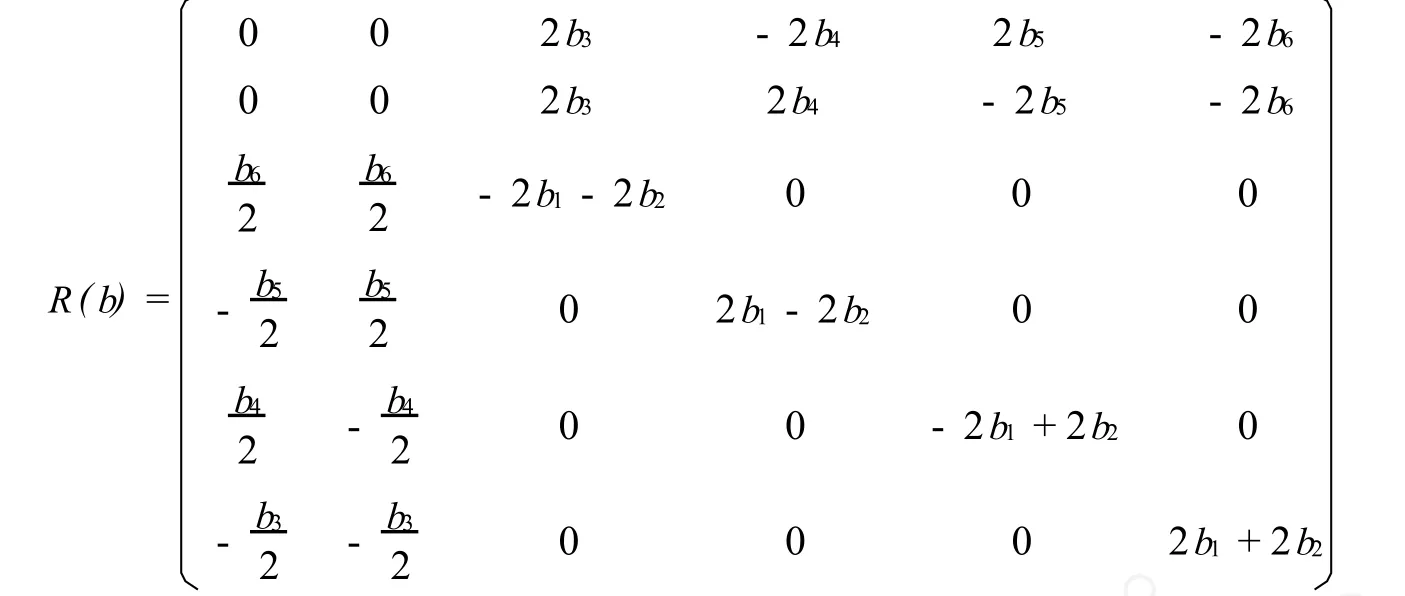
其满足等式

如果取

易验证方程(13)成立,即

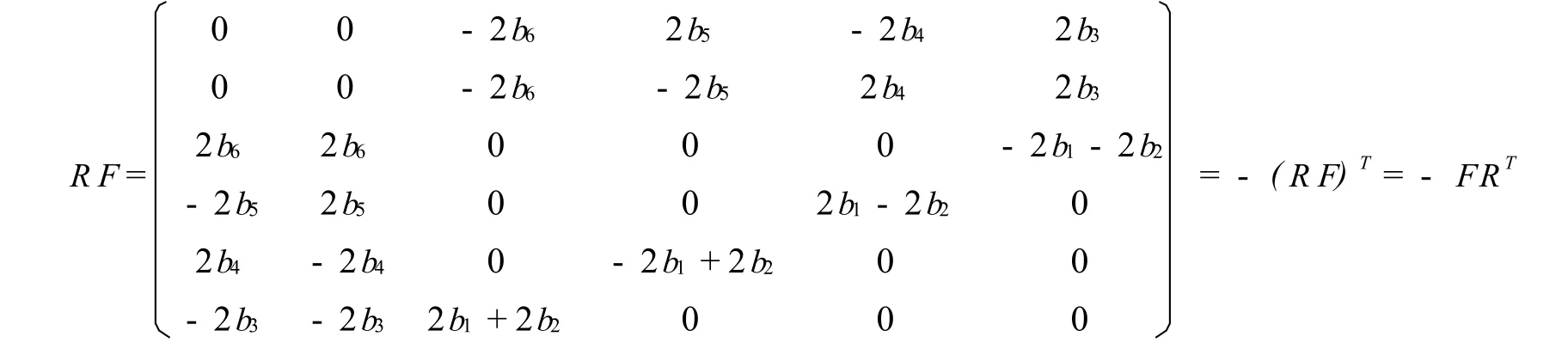
由(18)式我们可以得到下面的函数

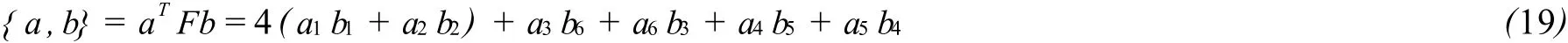
接下来,将利用李代数V6构造其Loop代数来得到两类新的Liouville可积方程族,并利用屠格式和二次型恒等式得到其哈密顿结构。

例1 第一类可积方程族

考虑下面的Loop代数和其应用

设

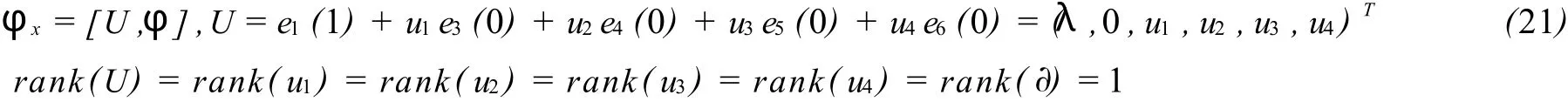
(21)和(22)式的相容性条件确定的静态零曲率方程即

其中V的解如下

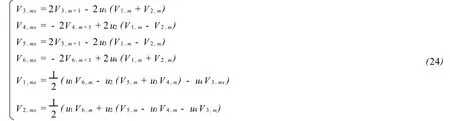
取

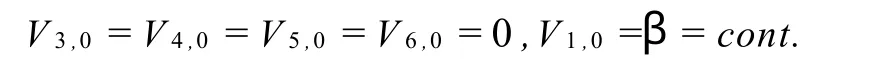
由(24)可得

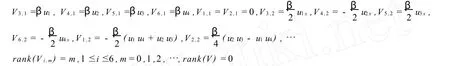
令

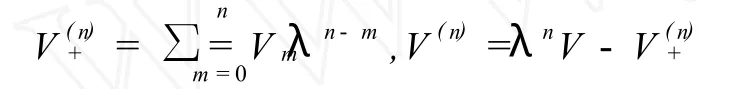
则方程(23)可分解为下面的形式

上式左端所含基元阶数≥0,右端所含基元阶数≤0。因此,我们可以得到

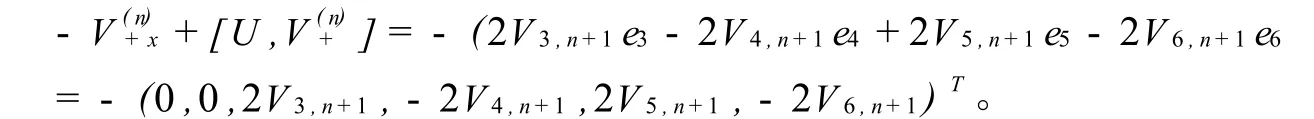
确定进化方程的Lax可积方程族

由(24)容易得到递推关系

其中

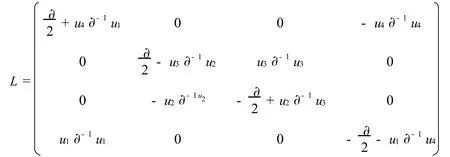
下面,推导(27)式的哈密顿结构。

记

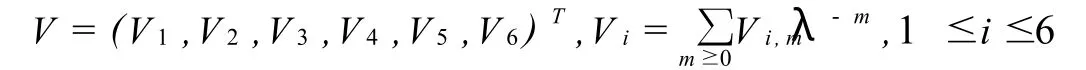
直接计算可得

把上式代入二次型恒等式(16)可得

根据文献[11]中求常数γ的方法,可以得到

比较(29)式中λ-n-2的系数可得

沟通交流是集体备课的核心，也是其区别于个人备课方式的最大特征.集体备课可以实现集中备课组所有老师的智慧与成果，实现取长补短，共同提高.在主要发言人对整节课的教学环节进行设计之后，备课组长就可以组织所有老师开展交流，对方案的不足进行补充，比如新课导入的方式、重难点的突破路径、习题的设计与选择等.

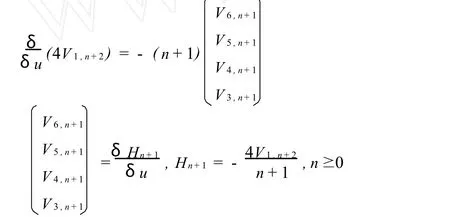
这样,方程族(27)可写成哈密顿结构

依照文献[5],任一 Hk(k≥1)是(30)的守恒密度且任意的 Hm,Hm是两两对合的。经过复杂的计算可得 JL=L＊J。因此,方程族(30)是Liouville可积的。

例2 第二类可积方程族

在这一部分中我们将考虑如下不同于(21)和(22)中Lax等谱问题的U和V

解方程

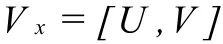
可得Vi,m的递推关系

取

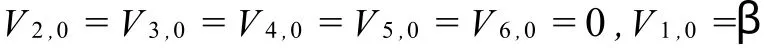
由(31)可得

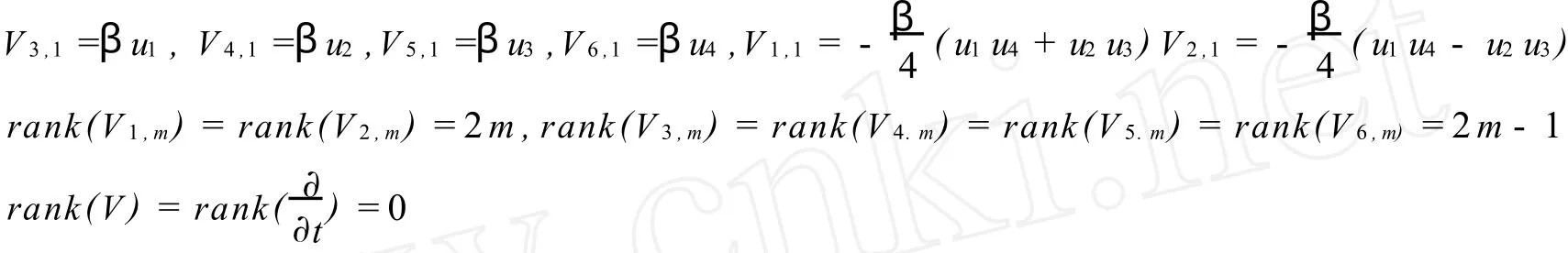
记

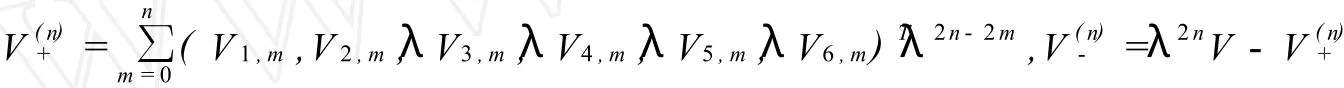
可写成

上式左端所含基元阶数 ≥0,右端所含基元阶数≤1。因此,我们可以得到

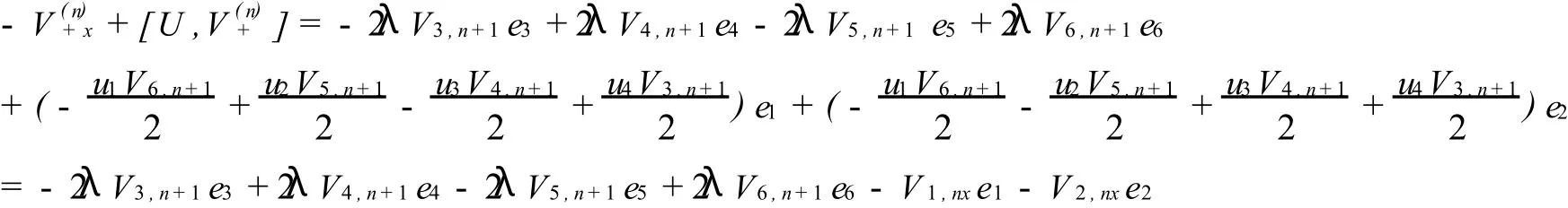
由零曲率方程

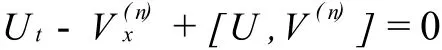
可得

由(31)式可得到下面的递推关系

通过计算可得

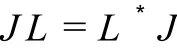
因此,Lax可积方程族(33)是Liouville可积的。

接下来利用二次型恒等式推导(33)式的的哈密顿结构。

记

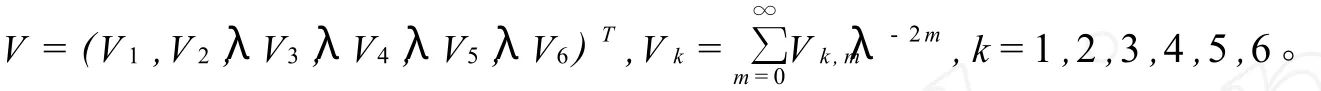
容易计算得

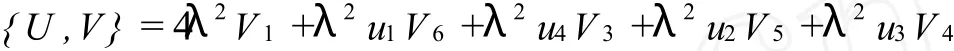
把上式代入二次型恒等式可得

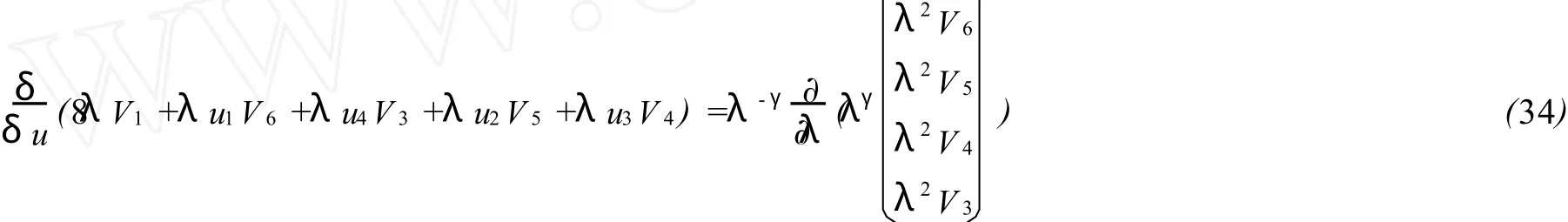
根据文献[11]中求常数γ的方法,可得

因此γ=0。

比较(34)式中λ-2n-1的系数可得

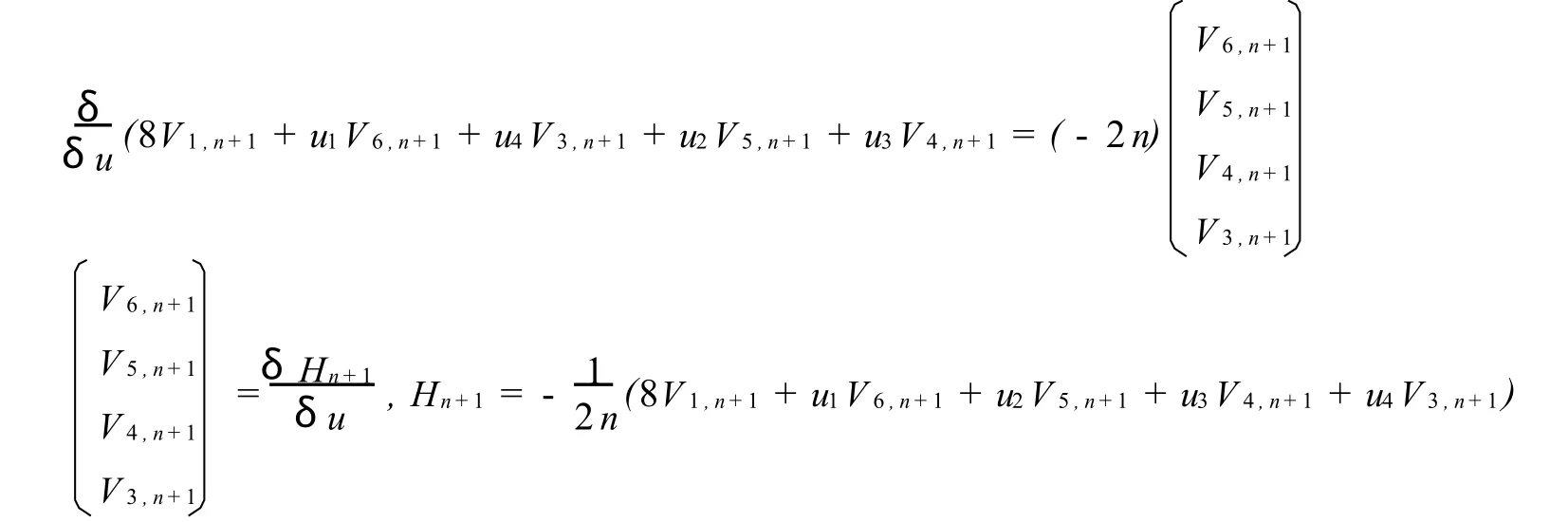
因此,方程族(33)可写成下面哈密顿结构

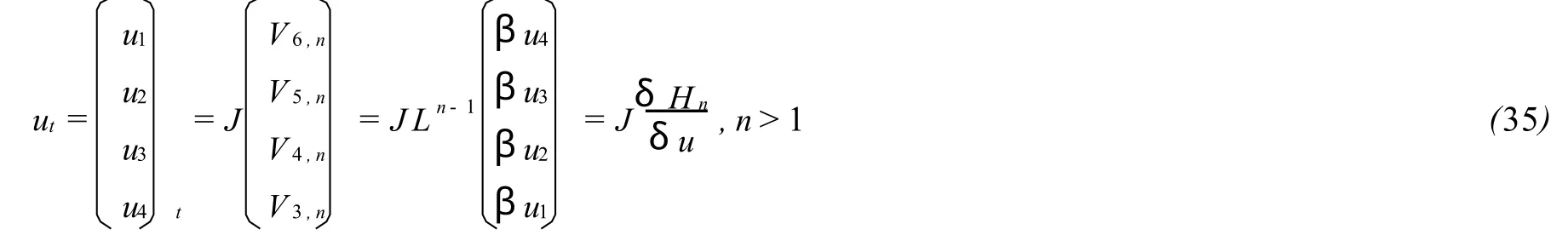
记 H1=-4V1,1,可得

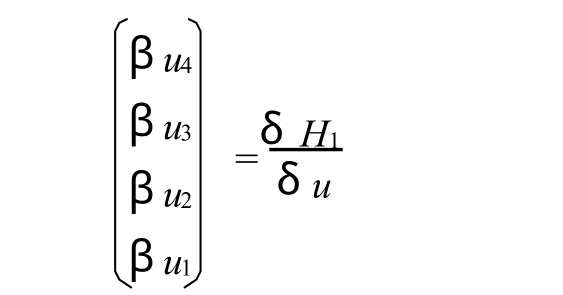
因此(35)式对于n≥1是成立的。

3 结论

本文介绍一类新的6维李代数并构造了两类相应的Loop代数。作为其应用得到了两类进化方程的可积方程族并利用二次型恒等式得到其哈密顿结构。利用本文的李代数还可以建立其他的Loop代数并利用本文的方法得到其他的新的可积系统。因此本文的方法有广泛的应用。

[1]Newell A C.Solitons in mathematics and physics[M].Philadelphia:SIAM,1985.

[2]Ablow itz M J,Segur H.Solitons and inverse scattering transfo rm[M].Philadelphia;SIAM,1981.

[3]Wadati M,Konno K,Ichikawa Y H.A Generalization of inverse scattering method[J].J Phys Soc Jpn,1979,(46):1965.

[4]Wadati M,Konno K,Ichikawa Y H.New integrable nonlinear evolution equations[J].J Phys Soc Jpn,1979,(47):1698.

[5]Tu G Z.The trace identity,a powerful tool for constructing the Hamiltonian structure of integrable systems[J].J Math Phys,1989,30(2):330.

[6]Ma W X,Fuchssteiner B.Integrable coup lings of the hierarchies of evolution equations[J].Solitons and Fractals,2003, (16):263.

[7]Ma W X.Integrable coup lingsof soliton equations by perturbations I.A general theory and app lication to the KdV hierarchy[J].Methods and App lications of Analysis,2000,(7):21-56.

[8]Guo F K,Zhang Y F.A unified exp ressing model of the AKNSand its expanding integrablemodel[J].Chaos Solitons and Fractals,2004,19(5):1207.

[9]Guo F K,Zhang Y F.A type of expanding integrable model of the A KNS hierarchy[J].Acta Physica Sinica,2002(51): 951.

[10]Guo F K,Zhang Y F.The quadratic-form identity fo r constructing the Hamiltonian structure of integrable systems[J]. J Phys A,2005,(38):8537.

[11]Guo F K,Zhang Y F.Two unified fo rmulae[J].Phys Lett A,2007,366:403.