“视图与投影”考点分析

224054 江苏省盐城市亭湖区永丰初中 唐耀庭

“视图与投影”考点分析

224054 江苏省盐城市亭湖区永丰初中 唐耀庭

《视图与投影》虽然是新教材的新内容，但已成为近几年来中考命题的热点和必考的内容之一，就2010年各地中考命题来看，主要有以下几个考点.

1 考查物体的视图

例1 (2010年抚顺)有一个圆柱形笔筒如图1放置，它的左视图是

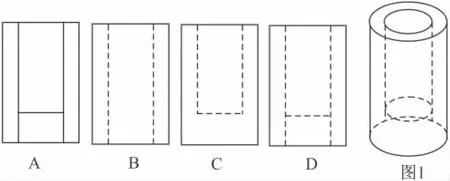
解 圆柱的左视图为长方形，那么从左面看可得到两个长方形，里面的长方形有3条边是虚线，故选C.

点评 本题考查了三视图的知识，左视图是从物体的左面看得到的视图，解答物体视图不仅要看物体的形状，同时也要注意题意的语言表述，结合实际情况.解答时首先要把它抽象为相应的几何体.三视图的实线与虚线是有讲究的，确实存在，但看不到的用虚线，看得见的用实线.

2 考查基本几何体的视图

例2 (2010年福州)下面四个立体图形中，主视图是三角形的是

解 本题考查了三视图的知识，主视图是从物体的正面看得到的视图，找到从正面看所得到的图形为三角形即可.A.主视图为长方形，不符合题意;B.主视图为圆，不符合题意;C.主视图为三角形，符合题意;D.主视图为长方形，不符合题意;故选C.

点评 基本几何体是指那些简单的几何体，象圆柱、圆锥、圆台、球、正方体、长方体、三棱柱、三棱锥等这些常见的几何体，它们的各种视图的形状应做到了如指掌.但反过来要注意仅由一种视图并不能唯一确定它所对应的几何体.

图2

3 考查组合几何体的视图

例3 (2010年天津)图2是一个由4个相同的正方体组成的立体图形，它的三视图为

解 这是简单组合体的三视图.从正面看可得到:从左往右2列正方形的个数依次为2，1;从左面看可得到:从左往右2列正方形的个数依次为2，1;从上面看可得到:从上到下2行正方形的个数依次为2，1，故选B.

点评 掌握定义是关键.几何体的三视图是指从指定的角度、方向进行观看所看到的平面图形，该平面图形的形状是由所看到的各个部分的平面图形组成的，要特别注意各部分图形摆放的位置和方向，同时还要注意大小.

4 考查由视图想象组合几何体

例4 (2010年山东)如图3，是有几个相同的小正方体搭成的几何体的三种视图，则搭成这个几何体的小正方体的个数是

A.3 个 B.4 个

C.5 个 D.6 个

图3

解 从主视图看第一列两个正方体，说明俯视图中的左边一列有两个正方体，主视图右边的一列只有一行，说明俯视图中的右边一行只有一列，所以此几何体共有四个正方体.故选B.

点评 由小正方体搭成的组合几何体是中考中有关视图命题的热点，由部分视图推测整个组合几何体至少或至多需要小几何体的个数具有一定的难度，解决时需要较强的想象力，想象出整个组合几何体的形状.做这类题时要借助三种视图表示物体的特点，从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状，综合分析，合理猜想，结合生活经验描绘出草图后，再检验是否符合题意.

5 考查太阳光、灯光与影子(平行投影)

例5 (2010年安顺)小华拿一个矩形木框在阳光下玩，矩形木框在地面上形成的投影不可能的是

分析 太阳光线可以看成平行光线，像这样的光线所形成的投影称为平行投影.在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，据此进行分析.

解 矩形木框在地面上形成的投影应是平行四边形或一条线段，即相对的边平行或重合，故A不可能，即不会是梯形.故选A.

点评 本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应视其外在形状，及其与光线的夹角而定.

6 考查灯光与影子(中心投影)

例6 (2010年江苏)如图4，夜晚，小亮从点A经过路灯C的正下方沿直线走到点B，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间的函数关系的图象大致为

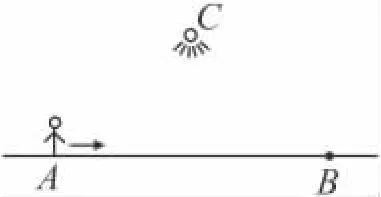
图4

分析 物体在灯光下所形成的投影为中心投影，解决投影有关题目，其最重要的是确定投影中心.

图5

点评 本题考查函数的图象函数的图象、中心投影，解决此类问题的关键是抓住横轴与纵轴的意义.

7 考查视点、视角和盲区

例7 (2010年本溪)“汽车驾驶员的座位设在前面而不是后面”这与“站得高，看得远”从数学原理上来说是为了＿＿.

分析 “汽车驾驶员的座位设在前面而不是后面”是为了增加驾驶员的视角，减少盲区，从而更有利于驾驶;在高处俯瞰时，视角会增大，而盲区相应减小，故“站得高，看得远”也是为了增大视角，减少盲区.

解 “汽车驾驶员的座位设在前面而不是后面”这与“站得高，看得远”从数学原理上来说是为了增大视角，减小盲区.

点评 能够联系实际问题来理解视角、盲区的定义是解答此题的关键.

20110323)