从一道中考题学习解“找规律题”

441123 湖北省襄阳市襄州区黄集镇初级中学 张昌林

从一道中考题学习解“找规律题”

441123 湖北省襄阳市襄州区黄集镇初级中学 张昌林

数学题，可以分为两大类，一类是应用数学规律题，一类是发现数学规律题.应用数学规律题，指的是需要学生应用以前学习过的数学规律解答的题目.发现数学规律题，指的是与学生以前学习的数学规律没有什么关系，需要学生先从已知的事物中找出规律，才能够解答的题目.学生所做数学题，绝大多数属于第一类.

由于发现数学规律题，能够增强学生的创造意识，提高学生的创新能力.因此，近几年来，人们开始逐渐重视这一类数学题.尤其是最近两年，全国多数地市的中招考试，都有这类题目.研究发现数学规律题的解题思想，不但能够提高学生的考试成绩，而且更有助于创新型人才的培养.

本文以一道2010年青岛的中考试卷里的找规律题为例，解析一下找规律题的几种解法.

例 (2010年山东)如图1，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，则摆第6个图案需要＿＿枚棋子，摆第n个图案需要＿＿枚棋子.

图1

1 一般方法——单纯从数的角度(点的角度)看

标出序列号:找规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律.找出的规律，通常和序列号有关.所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘.

图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

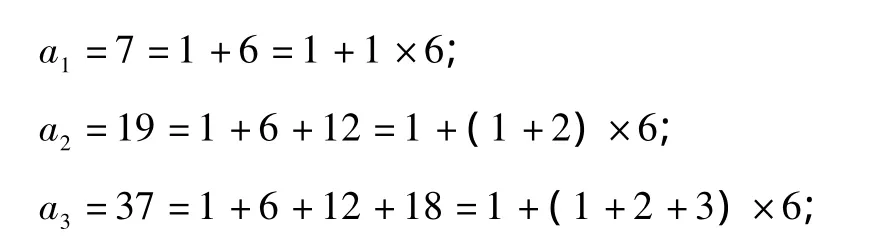
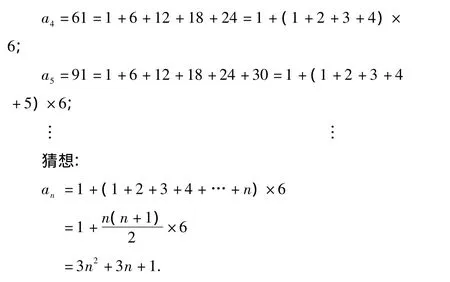
说明 上述方法需要有较强的数感.此解法虽然有一定的难度，但却是此类题的通用解法.

2 几何方法——从“数形结合”的角度看

从“形”的角度看方法较多，让人有“横看成岭侧成峰，远近高低各不同”的感觉.现在以第三个图为例进行说明.与方法1那样把变量和序列号放在一起加以比较.

2.1 横看——从“线”的角度看

如图 2，图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

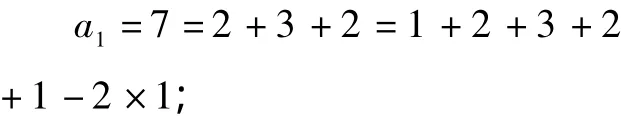
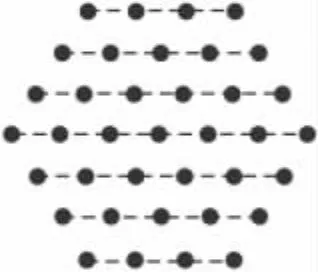
图2

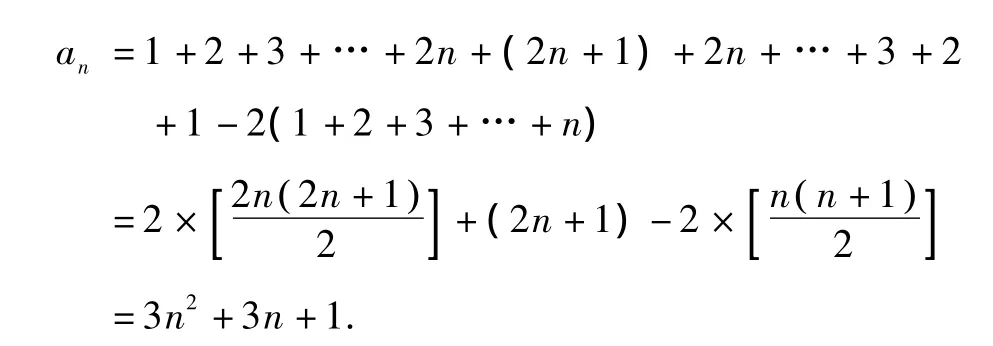
点评 把数和形结合起来跟上面的方法比更容易找出数的规律.

2.2 从三角形的角度看——把图形分成六个等边三角形

如图 3，图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

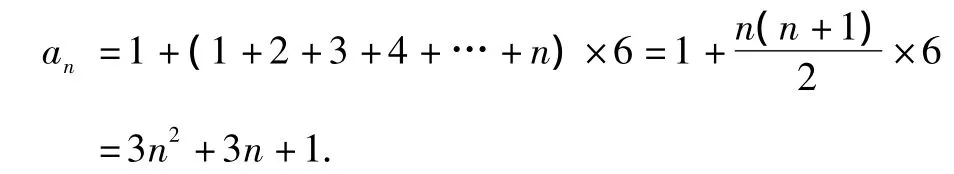
说明 把数和形结合起来跟上面的方法比又显得简单些了.

2.3 从平行四边形的角度看——把图形分成三个平行四边形

如图 4，图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

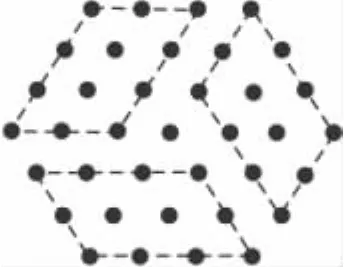
图4

点评 把数和形结合起来跟上面的方法比更显得简单些了.

2.4 从六边形的角度看——把图形分成六边形

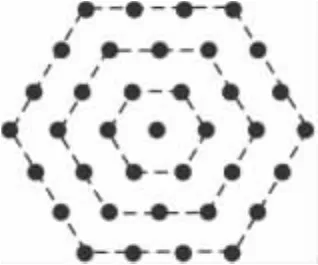
图5

如图 5，图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

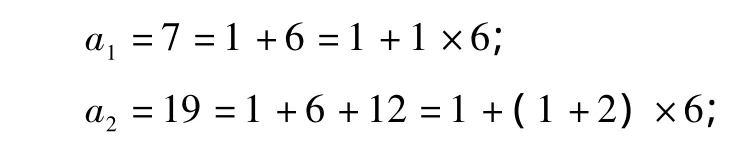
点评 这样做和“方法1”和“方法2，1.横看——从“线”的角度看:”来比有优势，但和“方法 2.2，2.3”比并不简单.

2.5 分成三个不同的平行四边形来看

如图 6，图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

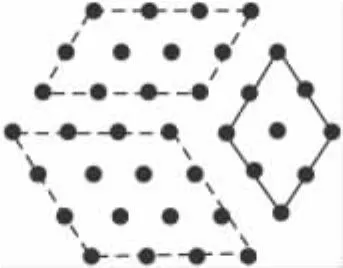
图6

点评 这样做比上面的方法都简单最就有规律性.从上面“数形结合”的角度看问题，我们会发现比单纯从数(点)的角度看问题更容易找出问题的规律性.关于这道题的解法还有很多种，同学们可以试着从梯形或组合图形的角度看一看，如图7.希望同学们有新的发现!

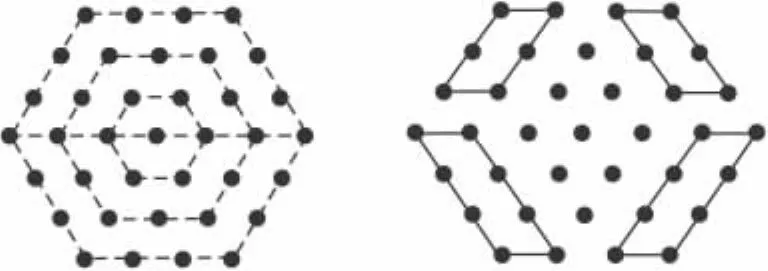
图7

3 坐标方法——从函数的角度看

图的序列号:1，2，3，4，5，…

图中点的数目:7，19，37，61，91，…

我们会发现序列号和对应图中点的数目很有规律地排列着，它们之间存在着二次函数的关系.不妨设点的数目y和图的序列号x的关系为:

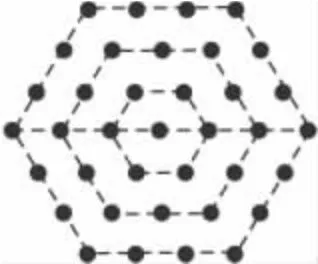
图8

点评 学习了二次函数可用此法，这样做并不见得简单实用，但也是一种解题途径.

20110402)