基于冲杯边缘线的各向异性参数反求
崔付刚 李光耀 刘迪辉 李方义
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
基于冲杯边缘线的各向异性参数反求
崔付刚 李光耀 刘迪辉 李方义
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
提出一种基于试验冲杯边缘线反求薄板金属各向异性参数的方法。首先通过冲杯试验及逆向技术获取冲杯试件边缘线;然后以各向异性参数为反求变量,以仿真冲杯边缘线与试验冲杯边缘线的逼近程度为目标函数,结合数值仿真和多岛遗传算法反求各向异性参数。算例表明,该方法能够在简单试验条件下快速地获得具有较高精度的材料各向异性参数,对提高冲压仿真的预测精度有一定借鉴意义。
反求;薄板金属;各向异性参数;多岛遗传算法
0 引言
在薄板金属冲压成形过程中,各向异性对其成形有显著的影响。凸缘制耳、断裂位置和极限拉深高度等,都与板材的各向异性造成的塑性流动的改变相关[1]。因此,为了提高数值仿真的精度,尤其是高强度钢、铝镁合金等高各向异性材料的广泛应用,准确获得各向异性参数显得很有必要。
各向异性参数的传统获取方法是,取不同方向上的标准试件做拉伸试验,根据试验数据,在假定满足特定应力应变关系下,解析求得材料的参数。这种方法属于小应变速率下的准静态试验,且不同伸长率下测得的参数值是有差别的[2]。但是薄板冲压是一个大应变、复杂各向异性的三维弹塑性变形过程,因此这种小应变下获得的且具有波动性的材料参数并不能反映材料的成形特性。
十几年来,基于优化的反求理论对准确快速地获得材料参数提供了新的方法。Zhou等[3]反求了复合材料A l2O3sf/LY12在热成形中的本构参数;高晖等[4]基于杯突试验,结合近似模型和遗传算法反求了材料参数;刘迪辉等[5]在不带肩试样拉伸试验的基础上反求了Barlat1991模型的材料参数。上述研究都是基于力-位移的试验测量值与仿真计算值之差在最小二乘意义上最小的原理进行反求的,而准确获得力-位移数据的试验装置复杂、价格高,因而限制了上述方法的应用。
冲杯成形是研究各向异性的典型成形过程。本文在简单冲杯试验的基础上提出了基于冲杯边缘线反求薄板金属厚向异性系数r0、r45、r90的方法。首先,通过冲杯试验获取试件边缘线并建立仿真模型;然后,以各向异性系数为反求变量,以仿真冲杯边缘线与试验冲杯边缘线的逼近程度为目标函数建立优化模型,并选用多岛遗传算法进行优化反求;最后以先进高强度钢DP800为例,比较了传统拉伸试验获得的参数下与反求参数下的仿真冲杯边缘线,及该两组参数下仿真中冲头的力-位移曲线,结果表明该方法是可行有效的。
1 反求模型的建立
1.1 冲杯仿真模型
为了缩短正问题的计算时间,根据冲杯的对称性,建立其相应的1/4模型。板料网格的划分规则如图1所示。网格单元选取Belytschko-Tsay壳单元。考虑仿真模型中能同时设置待反求参数r0、r45及 r90,材料模型选 3-Parameter¯Barlat模型。正问题的求解可在商用软件LS-DYNA中进行。

图1 冲杯的数值仿真模型及板料网格划分规则
为了选用较大的板料网格以缩短正问题的计算时间,我们研究了冲杯边缘对网格大小的敏感性。图2中,纵横坐标分别表示相对轧制方向为0°、90°方向上的冲杯外缘坐标,由图 2可以看出网格尺寸(边长)w 为 1mm、1.5mm、2mm、2.5mm时的边界相差无几,其一次正问题的计算时间分别为 52s、37s、32s、28s。统筹计算效率和计算精度,反求模型的板料网格尺寸选用2mm。

图2 网格尺寸对冲杯边缘的影响
1.2 厚向异性系数
本文定义的反求参数为厚向异性系数R,它包括r0、r45、r90,它是板材拉伸试件在拉伸试验中宽度方向应变εb与厚度方向应变εt之比,即
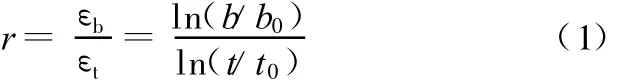
式中,b0和t0分别为试样原始宽度和厚度;b和t分别为试件在某一变形时刻的宽度和厚度。
1.3 反求用优化模型
基于优化的反求方法的基本思想就是通过优化算法优化参数,使仿真响应值逼近试验值。本文反求中用到的优化模型为

2 反求流程及其关键技术
2.1 试验冲杯边缘的获取及其离散化
试验冲杯的边缘是基于逆向工程技术获取的。逆向工程是指在没有设计图纸或设计图纸不全以及没有CAD模型的情况下,按照现有产品样件或事物模型,利用3D数字化设备快速准确地测量出实物表面的三维坐标点,并根据这些坐标点通过几何建模方法重建实物CAD模型的过程[7-9]。获取试验冲杯边缘线的流程如图3所示。文中的点云是通过三坐标激光扫描仪获取的。考虑与仿真模型的一致,只选取边缘线的1/4。

图3 逆向获取冲杯边缘线的流程
将选取的试件边缘线离散为等间距的线段,其节点总数与仿真模型中板料边缘的采样节点数相等。最后导出边缘线的节点坐标数据,将其记为Uexpi,其中U i=(xi,yi)。
2.2 多岛遗传算法
在反求中最优参数的搜寻采用多岛遗传算法(mu lti-island genetic algorithm,M IGA)进行。与传统遗传算法相比,多岛遗传算法将整个进化种群划分为若干子种群,称之为岛屿,在各岛屿内部对子种群进行选择、交叉与变异操作,并定期在各岛屿之间迁移按规定比例选择的个体,然后继续进行传统遗传算法的操作。通过这种方式,维持了群体的多样性,增强了算法的多峰搜索能力,从而尽可能地避免局部最优解,抑制早熟现象的发生[10]。
2.3 反求流程[11-13]
本文将上述数值仿真模型、优化模型、边缘获取技术及多岛遗传算法相结合,提出了基于冲杯边缘线的各向异性参数反求方法,其技术流程如图4所示。

图4 反求方法的技术流程
3 各向异性参数反求算例
3.1 冲杯试验
验证反求方法的试验材料是板厚为1.2mm的高强度钢DP800,试验模具选用Swift杯形件拉深试验的标准模具III,其关键尺寸如图5所示。

图5 冲杯试验模具的关键尺寸
试件的冲压深度为25mm,压边力为3kN。试验在美国M TS公司制造的压机试验台上进行,该压机采用计算机软件控制和液压伺服闭环设计。冲头的力和位移可分别通过力传感器和位移传感器获得,试验后处理计算机自动输出的力-位移数据,以方便验证该反求方法的可行性及其精确度。
3.2 反求参数及其分析
利用上述反求方法反求了试件的各向异性参数,图6所示为目标值的迭代收敛过程。从表1的反求结果可以看出,在反求参数搜索范围比较大的情况下,还是得到了理想的收敛值。
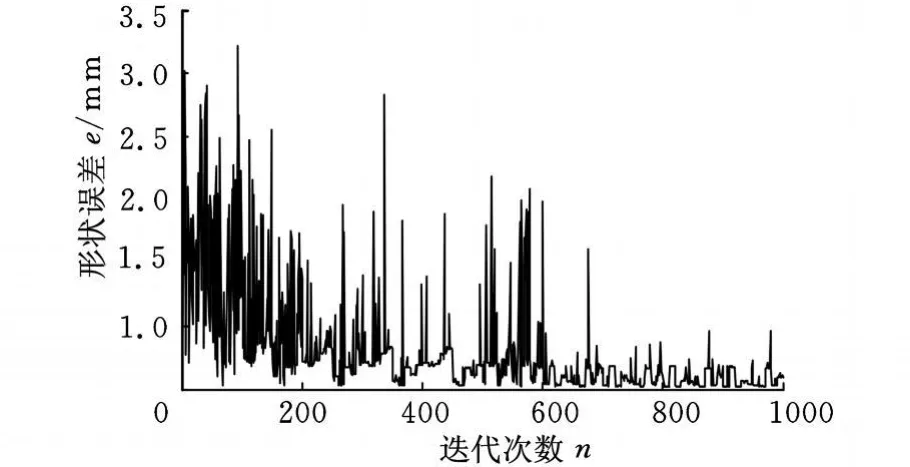
图6 迭代收敛过程

表1 反求参数的初始值/搜索范围及收敛值
从表1可以看出:与传统拉伸试验获得的材料参数相比,反求参数有一定差别。其原因主要有:①冲压成形是一个高度非线性的复杂过程,仿真中的材料模型对材料力学性能的描述有限且边界条件也不能准确描述试验状态;②传统拉伸试验获得的各向异性参数是在某一定应变范围内的平均值,但是这组以试验为参考迭代仿真模型反求的参数更有利于提高有限元仿真的精度。图7给出了反求参数下及试验参数下的仿真冲杯边缘线与试验冲杯边缘线的对比,纵横坐标分别表示相对轧制方向为0°、90°方向上的冲杯外缘坐标,由图7可见,反求参数下的仿真结果精度更逼近试验结果。

图7 不同参数下的冲杯边缘比较
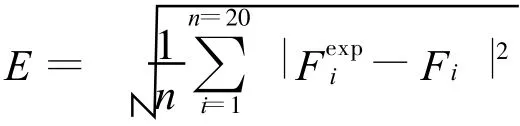
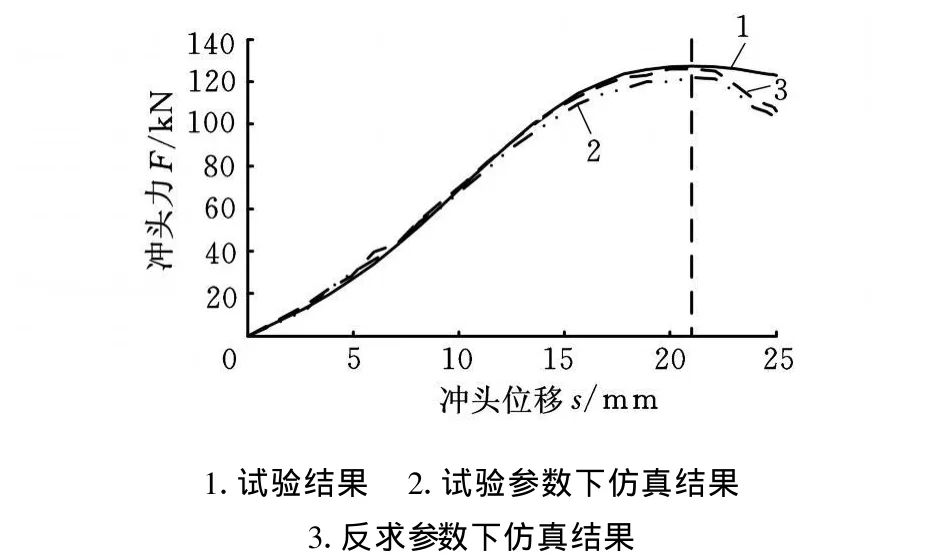
图8 不同参数下的力-位移曲线比较
4 结论
提出了基于冲杯边缘线反求薄板金属材料各向异性参数的方法。将仿真模型和多岛遗传算法相结合,通过比较仿真冲杯边缘与同步试验冲杯边缘的重合程度实现了以厚向异性参数r0、r45、r90为目标参数的反求。以高强度钢DP800为例,分析了传统拉伸试验获得的参数下及反求参数下的仿真冲杯边缘线及力-位移曲线逼近相应试验结果的程度,结果表明,提出的反求方法可以在简单的试验条件下快速精确地获得各向异性参数。由于其正问题调用的是真实仿真模型,精度较高,且方法较为简单,故应用该方法获得的参数,在高各向异性材料的应用仿真中,尤其在诸如冲压等大应变的工程问题中,对提高仿真精度可提供一定的借鉴。
[1] 李大永.板材冲压过程中回弹/制耳的数值研究/镁合金汽车零件强度分析及锻造成形仿真[D].上海:上海交通大学,2002.
[2] 崔令江.汽车覆盖件冲压成形技术[M].北京:机械工业出版社,2003.
[3] Zhou Jim ing,Qi Lehua,Chen Guoding.New Inverse Method for Identification o f Constitutive Parameters[J].T ransactions o f Non ferrous Metals Society o f China,2006,16:148-152.
[4] 高晖,郑刚,李光耀.基于响应面方法的材料参数反求[J].机械工程学报,2008,44(8):102-105.
[5] 刘迪辉,钟志华.Barlat1991模型的材料参数反求[J].机械工程学报,2006,42(4):47-51.
[6] Padmanabhan R,O liveira M C,Baptista A J,et al.Blank Design for Deep Draw n Parts Using Parametric NURBS Surfaces[J].Journa l of Materia ls Processing Technology,2009,209:2402-2411.
[7] 金涛,童水光.逆向工程技术[M].北京:机械工业出版社,2003.
[8] 张红金.逆向工程技术的应用[J].电子产品可靠性与环境试验,2005,23(5):25-29.
[9] 石秋华,程运波,王慧君.逆向工程的关键步骤和主要技术[J].中国科技博览,2009(4):106-107.
[10] 孟祥众,石秀华,杜向党.基于遗传算法的振动主动控制优化方法研究[J].计算机测量与控制,2008,16(1):74-77.
[11] 曹银锋,李光耀,钟志华.金属成型材料参数的反求技术[J].计算力学学报,2004,21(3):291-302.
[12] Anghileri M,Chirw a EC,Lanzi L,et al.An Inverse Approach to Identify the Constitutive Model Parameters for Crashworthiness Modelling of Composite Struc tures[J].Composite Structures,2005,68:65-74.
[13] 刘迪辉,汪晨,李光耀.薄壁钢管材料参数反求[J].中国机械工程,2008,19(6):688-690.
Inverse Approach to Identification of Anisotropy Parameters Based on Flange Edge of Drawing Cup
Cui Fugang Li Gangyao Liu Dihui Li Fangyi
State Key Laboratory of A dvanced Design and Manufacture for Vehicle Body,Hunan University,Changsha,410082
Based on flange edge of draw ing cup,an inverse approach to identify anisotropy parametersw as presented.This inverse approach achieved the flange edge of drawing cup through draw ing cup experim ents and reverse engineering technology,and taking the coefficient of normal anisotropy as the inverse variables,the differences of flange edge between the sim ulation and experiment as the objective function,numerical simulation and multi-island genetic algorithm were com bined to identify the anisotropy parameters.An examp le w as performed to dem onstrate that this method can identify these parameters rapid ly under sim ple experimental conditions.Using the parameters inversed by thismethod can imp rove the p recision of sheetmetal form ing sim u lation.
inverse approach;sheetmetal;anisotropy param eter;m ulti-island genetic algorithm
O34;TG38
1004—132X(2011)06—0732—04
2010—05—13
教育部长江学者和创新团队发展计划资助项目(53110505037);科技部国际科技合作重点项目计划资助项目(2008DFB50020);汽车车身先进设计制造国家重点实验室自主研究课题(70870006)
(编辑 苏卫国)
崔付刚,男,1986年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。主要研究方向为薄板冲压成形及回弹的有限元仿真计算等。李光耀,男,1963年生。湖南大学汽车车身先进设计制造国家重点实验室主任、教授、博士研究生导师。刘迪辉,男,1975年生。湖南大学汽车车身先进设计制造国家重点实验室副教授、博士。李方义,男,1978年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。

