一种基于灰色预测模型的预测桁架结构疲劳寿命的数值方法
李 源 韩 旭 姜 潮 王林军
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
2.国防科学技术大学,长沙,410072
一种基于灰色预测模型的预测桁架结构疲劳寿命的数值方法
李 源1,2韩 旭1姜 潮1王林军1
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
2.国防科学技术大学,长沙,410072
以超静定桁架结构为研究对象,提出了一种基于灰色预测模型(GM)的预测桁架结构疲劳寿命的数值方法。分析了对数阶次处理的原则,确定了适合桁架结构疲劳寿命预测的阶次;修正了临界失效元件识别参数的定义,使约界参数的选择更加精确;在主要疲劳失效模式搜寻前增加了临界失效内力判据,减小了识别失效模式算法的计算量;应用改进的灰色预测模型估计威布尔分布函数,预测出不同可靠度下的桁架结构疲劳安全寿命。所提供的十杆桁架结构的算例证明了该数值方法的有效性。
超静定桁架结构;对数准则;灰色预测模型;威布尔分布;疲劳寿命预测
0 引言
关于结构系统疲劳寿命的可靠性分析,目前研究较多的是结构系统疲劳失效概率的计算方法,很少有学者以数值方法来预测不同可靠度下结构系统的疲劳寿命[1-2]。关于预测疲劳载荷作用下结构系统寿命的数值方法的研究主要包括:①识别结构系统主要疲劳失效模式的算法研究;②以各主要失效模式疲劳寿命作为样本值,对结构疲劳寿命分布参数进行估计的方法研究。
对于工程中常用的超静定桁架结构,识别主要疲劳失效模式的算法的选择至关重要。国内外学者的研究多集中在静载作用下的结构主要失效模式识别[3-6]。吕海波、姚卫星率先提出了一种枚举桁架结构系统疲劳失效模式的工程准则法,并以十杆桁架结构为例,采用失效概率作为判据来搜寻得到结构的主要失效模式[7]。李洪双等[2]优化了工程准则法,提出了一种以临界失效元件识别参数作为判据的对数准则法。对数准则法简单实用,但在临界失效元件识别参数的定义中,未考虑对数的阶次对临界参数定义精度的影响。另外,只有所受内力高于其疲劳强度的元件才会发生疲劳破坏,但对数准则法在每次疲劳失效模式搜寻开始前需计算每个元件的寿命,导致计算量较大。
在桁架结构寿命分布参数估计方法研究方面,文献[2]假定结构疲劳寿命分布参数服从对数正态分布,采用单侧系数法得到了不同可靠度下的疲劳寿命。但对于单个元件疲劳失效引起全局失效的桁架结构的寿命估计,假定服从三参数威布尔分布更符合工程实际。且威布尔分布函数存在最小寿命,即100%可靠度的寿命,符合疲劳破坏的实际情况[8]。
针对以上问题,本文研究了对数阶次对识别参数精度的影响,修正了临界失效元件识别参数定义,在主要疲劳失效模式搜寻前增加了临界失效内力判据,提出了一种改进的对数准则法。进而以不同失效模式疲劳寿命值为母体样本值,应用改进的灰色理论模型对桁架结构的威布尔分布参数进行估计,预测出不同可靠度下的结构安全寿命。
1 数据的对数处理原则
数据的对数处理可提高其线性化程度,降低不确定性的影响。文献[9]中提出了数据的对数处理原则:
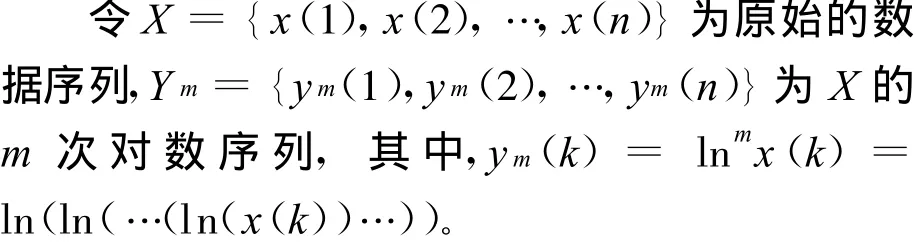
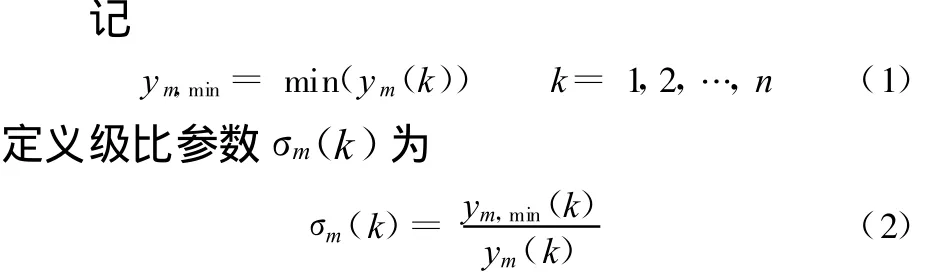
级比参数σm(k)与下文的临界元件失效识别参数的定义相一致。可通过选取合适的m,使得σm(k)变化区间到达满意的精度。
取本文算例中的一组疲劳寿命值序列X来进行验证。令 X=(x(1),x(2),x(3),x(4),x(5),x(6))=(0.3625×106,0.3812×106,0.3953×106,0.8449×106,0.9725×106,2.8422×106),根据上述计算公式,当对数的阶次m分别取1、2、3时,得到的 ym(k)和σm(k)值如表1所示,其中,带下划线的数字为相应的ym,min(k)值。

表1 对数序列值及级比参数值(m=1,2,3)
当阶次m分别取1和2时,σm(k)的变化区间为[0.8594,1]和[0.9439,1],比较可得m=2时的区间取值范围变小,选取的约界参数更加精确。文献[2]中取一阶对数,确定的约界参数的值分别为0.8和0.9,本文中取二阶对数,约界参数的值可提高到0.95和0.98。
但阶次m的值并非越大越好,过大的m会使lnmx(k)过分减小,这样σm(k)反而会减小,表1表明:当m=3时,σ3(k)反而比σ2(k)有所下降。对本文中研究的问题,取二阶对数已能满足精度要求。
2 识别主要疲劳失效模式的算法
2.1 确定第1级失效元件
假设一个桁架结构含有L个元件,受到疲劳载荷的作用,使用有限元方法进行内力分析后,得到每个元件的循环应力分别为

(1)当元件所承受的循环应力高于其疲劳极限时才会产生疲劳破坏。临界失效内力判据为

式中,σfailure为元件的疲劳极限。
为了提高效率,只取满足临界失效内力判据的元件进行计算。
(2)由S-N曲线得到上步所求的各个元件的疲劳寿命为n1,1,n1,2,…,n1,L,取

取满足不等式C≤Ci≤1的元件作为第1级失效元件,其中常数C为约界参数(contro l am bit parameter,CAP),其值应视后续失效元件的破坏概率的大小而定。本文中取二阶对数后可使约界参数限制在精度较高的区间。CAP的取值大小将影响结构系统的失效路径和总的安全疲劳寿命评价[10]。
2.2 失效历程第p+1级临界元件的确定
设此时结构在疲劳载荷作用下,在 p+1级之前沿某一失效路径已有k1,k2,…,kp共p个元件失效,失效历程各阶段载荷所作用的时间分别为n1,n2…,np。
(1)去除最近失效的元件kp,结构的载荷将重新分配,尚未失效的元件将承担原由失效元件kp所承担的那部分载荷,根据有限元方法确定尚未失效元件ki(i=p+1,p+2,…,L)的循环应力Sp+1,ki。同样地,取满足临界失效内力判据S1,i≥σfailure的元件进行计算。
(2)在k1,k2,…,kp共p个元件失效的过程中,每一个元件失效都会引起尚未失效元件所受应力的变化,因此,尚未失效的元件已承受了 p级循环载荷的作用。此时依据M iner线性疲劳损伤理论,计算桁架结构未失效元件总的疲劳累积损伤。定义失效历经第p级而未失效的元件ki的累积损伤为Dp,ki:


同理,取满足不等式C≤Ci≤1的元件作为第p+1批失效元件。
2.3 停止搜索条件
如果当q级元件失效后,下一级失效过程中的某元件 Nq,failure的最大循环应力值Sq,failu re因大于等于σb(σb为元件的抗拉极限)而发生静力失效,从而导致整个结构失效,则停止搜索直接进入下一个阶段。如果min(nki)非常大,则认为该失效模式不会发生,停止搜索。在完成一个失效模式的搜索后,再重复以上过程直至枚举出全部失效模式。
设某一失效路径i有k个元件失效,将失效元件每一阶段所受循环应力水平Si,k及相关参数代入式(5),可以求得在各级循环应力水平下结构所经历的循环次数n1,n2…,nk,对应于这一失效模式i,桁架结构寿命Nik,failure可表示为
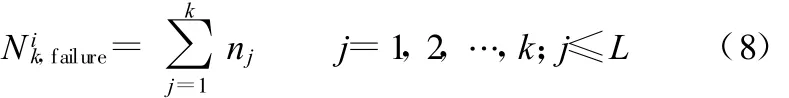
由此便可求得桁架结构疲劳寿命母体的多个最有可能出现的样本值。整个失效模式枚举的流程如图1所示。
3 基于GM的威布尔分布参数估计
由于存在三个参数,使得威布尔分布的参数估计有一定困难。在样本数量较小时,应用改进的灰色模型GM(1,1)灰色理论进行威布尔分布

图1 主要疲劳失效模式枚举法的流程图
参数估计,速度快且具有较高的精度[11]。
三参数威布尔分布的函数为

通过式(11)可预测出当R(x)为不同值时桁架结构的最小疲劳安全寿命。
对式(11)两边取自然对数可得:

按照文献[12]灰色理论方法,这与改进的灰色模型GM(1,1)的解的形式(式(16))完全一致:
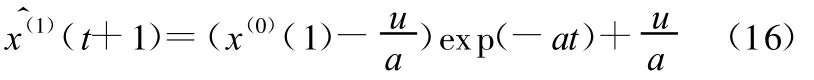
因此可以用一阶灰色模型直接建模法求得威布尔分布的三个参数,代入式(11)可预测出桁架结构在不同可靠度下的疲劳寿命。
4 算例
为验证改进方法的正确性,以文献[7]中的十杆桁架为例,进行了不同可靠度的桁架结构疲劳寿命预测。图2所示的十杆桁架的结构材料是LD10CS铝合金,其弹性模量为E=71GPa,泊松比为 μ=0.29,其断裂强度为 σb=552M Pa,屈服强度 σs=464MPa,各杆的长度 l=400mm,杆 1和杆2的横截面积为 A1=A2=200mm2,其余杆的横截面积为100mm2,在结构的右端承受着载荷值P max=25kN、循环应力比R=0.1的疲劳载荷,元件采用杆单元,失效方式为疲劳载荷破坏。材料的原始试验数据取自文献[13],应力集中系数K t=3,假定各杆光滑且不考虑尺寸效应,拟合的S-N的曲线为
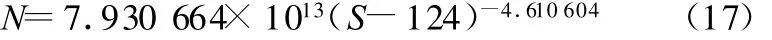

图2 十杆桁架结构图
4.1 枚举结构的主要失效模式
由有限元程序求出各杆的循环应力,依据式(17)计算相应的疲劳寿命,按照上述改进的对数准则法,得到的约界参数为0.95和0.98时的主要失效模式见表2。
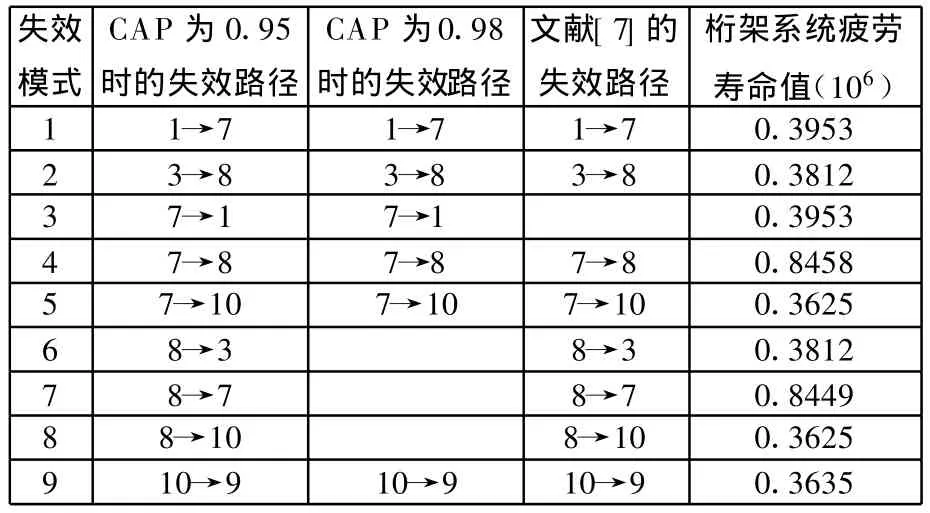
表2 十杆桁架主要疲劳失效模式
CAP值取得太大,会漏掉部分主要的失效模式,CAP值取得太小,会出现许多伪失效模式,因此CAP取值十分重要[10]。CAP取0.98时桁架结构的失效模式比取0.95时少了三个主要失效模式,因此该桁架系统CAP取0.95是合适的。采用本文中枚举失效模式的方法得到9个主要失效模式,与文献[7]中工程准则法确定的失效模式是一致的。依据Miner公式(式(5))计算出每个失效模式对应的疲劳寿命值(表2)。
4.2 威布尔寿命分布参数估计
以表2各个失效模式对应的疲劳寿命值为样本数据,采用上述基于改进的GM(1,1)灰色模型的参数估计方法得到的灰色模型为
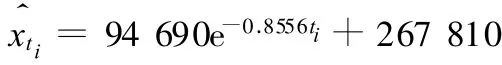
与式(15)对应可确定威布尔分布的三个参数。表3所示为基于灰色模型估计的威布尔寿命值及误差检验。从表3中可以看出,较大误差主要出现在样本8和样本9,按照文献[9]中的理论,因样本模型为非等间隔GM(1,1)模型,且两点都不在原点位置,可除去这两点,则参数估计模型平均误差在10%以内,即满足精度要求。

表3 基于灰色理论模型的威布尔参数估计
根据上述模型得到十杆桁架对应的威布尔分布函数的可靠度为
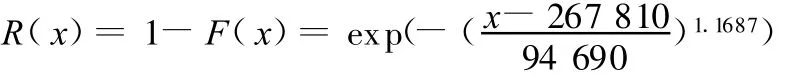
则根据式(12)可预测出桁架系统在不同可靠度下的疲劳寿命值,如表4所示。随着可靠度的逐渐提高,桁架结构的疲劳寿命逐渐降低,其中可靠度为100%的最小安全寿命值为0.2678×106。

表4 不同可靠度的结构系统疲劳寿命
5 结论
建立了一种基于GM的枚举桁架结构的主要疲劳失效模式的数值方法。在临界失效元件参数定义中,取二阶对数,使约界参数定义在精度较高的区间。在枚举主要疲劳失效模式的算法中,增加了临界失效内力判据,提高了算法的效率。应用改进的灰色理论模型估计威布尔寿命分布参数,可预测出不同可靠度下桁架结构疲劳寿命。最后以十杆桁架系统为例,验证了该数值方法的有效性。
[1] 安伟光,蔡荫林,陈卫东.随机结构系统可靠性分析与优化[M].哈尔滨:哈尔滨工程大学出版社,2007.
[2] 李洪双,吕震宙.预测复杂结构系统安全疲劳寿命的一种新数值方法[J].西北工业大学学报,2005,23(4):435-439.
[3] 赵维涛,安伟光.随机空间梁板结构系统静强度可靠性分析[J].兵工学报,2007,28(8):953-956.
[4] 安伟光,赵维涛,安海.随机结构系统综合考虑静强度、刚度和疲劳的多失效模式的可靠性分析[J].中国科学G辑,2007,37(4):516-526.
[5] Feng Y S.Enumerating Significant Failure Modes of a Structural System by Using Criterion Methods[J].Comp t.and Struct.,1998,30(5):1153-1157.
[6] 董聪,杨庆雄.结构系统疲劳裂纹形成寿命的可靠性分析[J].西北工业大学学报,1992,10(2):252-258.
[7] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.
[8] 刘惟信.机械可靠性设计[M].北京:清华大学出版社,2006.
[9] 邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002.
[10] 徐格宁,杨瑞刚.约界参数CAP对大型钢结构系统可靠性分析的影响[J].机械工程学报,2005,41(12):130-134.
[11] 严晓东,马翔,郑荣跃.三参数威布尔分布参数估计方法比较[J].宁波大学学报(理工版),2005,18(3):301-305.
[12] 郑荣跃,严剑松.威布尔分布参数估计新方法研究[J].机械强度,2002,24(4):599-601.
[13] 高镇同,蒋新桐,熊峻江,等.疲劳性能试验设计和数据处理[M].北京:北京航空航天大学出版社,1999.
A Numerical Method of Fatigue Life Prediction for Truss Structure Based on Grey M odel
Li Yuan1,2Han Xu1Jiang Chao1Wang Linjun1
1.State Key Laboratory of Advanced Design and M anufacturing for Vehicle Body,Hunan University,Changsha,410082
2.National University of Defense Technology,Changsha,410072
A numericalmethod o f fatigue life prediction of statically indeterminate truss structure based on gray model was estab lished herein.This paper analyzed p rinciples in dealing w ith the order of logarithm tim es,and determined right order of times to p redict fatigue lifetime.Then it amended the definition of the critical parameters identifying failureelements,so that the choices of bounded parameters were more accurate.Before the search of main fatigue failure modes,this paper added the critical failure internal stress criterion,reducing the calculation of recognition algorithm s for identifying failuremodes.Based on the improved grey model(GM),it estimated the Weibull distribution function,and calculated different safe lifetimes of truss structure system under different reliability degrees.The numericalexamp le of 10 truss structure show s the validity of the numericalmethod established.
statically indeterm inate truss structure;logarithm principle;grey model;Weibull distribution;fatigue life prediction
TB114.3;O346.2
1004—132X(2011)06—0710—05
2009—12—28
2011—01—19
国家杰出青年基金资助项目(10725208);长江学者和创新团队发展计划资助项目(531105050037);国家科技重大专项(2010ZX 04017-013-005);湖南大学汽车车身先进设计制造国家重点实验室自主课题(60870003)
(编辑 卢湘帆)
李 源,男,1983年生。湖南大学机械与运载工程学院博士研究生,国防科学技术大学指挥军官基础教育学院讲师。主要研究方向为材料及结构疲劳可靠性优化、车辆CAD/CAE工程。发表论文6篇。韩 旭,男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师,长江学者特聘教授。姜 潮,男,1978年生。湖南大学机械与运载工程学院副教授、博士。王林军,男,1982年生。湖南大学机械与运载工程学院博士研究生。

