平面二次包络环面蜗杆副应力及影响因素分析
张彦钦 张光辉
重庆大学机械传动国家重点实验室,重庆,400030
平面二次包络环面蜗杆副应力及影响因素分析
张彦钦 张光辉
重庆大学机械传动国家重点实验室,重庆,400030
基于弹塑性接触有限元理论,建立了多组适于蜗杆副静动态接触应力分析的模型,研究了载荷、齿形参数对齿间载荷分配系数和齿面应力分布的影响,计算了各级扭矩下不同包容齿数时的最大齿间载荷分配系数。研究结果表明:随着载荷的增大,齿间载荷分配趋于均匀;接触应力沿接触线从蜗轮齿根到齿顶呈“L”或“U”形分布;齿形参数对应力分布的影响不容忽略,以应力平均分布为目的的参数优化可通过对比有限元分析结果完成。得到了0.05~1.50倍额定扭矩下,包容齿数为3、5、7时的最大齿间载荷分配系数。
蜗杆;有限元;应力;齿间载荷分配
0 引言
平面二次包络环面蜗杆传动由于齿面形状及受力状态复杂,故其相关的应力分析很少见报道。文献[1]提出的接触应力解析算法虽然具有很好的借鉴作用,却无法分析应力的分布状态。近些年来,接触有限元法因为能够有效模拟传动副的应力分布状态而得到了广泛应用,如文献[2-3]分析了环面蜗杆副的接触应力,文献[4-5]分析了锥齿轮的应力分布状态,文献[6-7]采用有限元法得到了齿轮传动的应力分布。该类文献多以探讨有限元建模及计算方法为重点,应用有限元法分析齿面应力分布规律及其影响因素的文献很少见到。
笔者在前人分析的基础上,建立了蜗杆副静动态弹性接触有限元模型,通过对多组参数进行应力计算,研究了载荷、齿形参数对齿间载荷分配系数和齿面应力分布的影响,归纳了齿面应力分布的特点;计算了不同载荷下包容齿数与最大齿间载荷分配系数的对应关系,并分析了啮合时刻对最大齿间载荷分配系数的影响。
1 蜗杆副接触分析有限元模型
笔者根据啮合原理编制了蜗杆副参数化实体建模程序,由实体模型生成有限元网格模型,先后建立了蜗杆副理想装配状态和考虑了惯性和速度的动态接触有限元模型[8]。
如图1a所示,为了减小计算量,取蜗杆上参与啮合的一部分和蜗轮参与啮合的几个齿建立静力分析网格模型。载荷和约束均施加在内圈表面的节点上。设置约束如下:①限制蜗杆内圈的全部移动自由度,释放蜗杆内圈绕自身轴线的转动自由度;②约束蜗轮内圈的全部自由度;③将蜗杆副传递的转矩换算成圆周力施加在蜗杆内圈上。
如图1b所示,在做动力学分析时,把蜗轮上大部分轮齿简化为圆柱体,只留下参与啮合的轮齿,蜗杆齿采用整体仿真模型;将蜗杆和蜗轮的内圈均定义为刚性面,在蜗轮、蜗杆轴线上分别建立质心参考点。所有的约束和载荷均施加在刚性面上:①约束蜗杆、蜗轮内圈所有的平动自由度和2个旋转自由度,使其只能绕各自轴线旋转;②蜗杆内圈施加恒定的转速,蜗轮内圈加载恒定的阻力矩;③齿面间载荷的传递归为自动接触类型。

图1 蜗杆副有限元分析模型
蜗轮齿面上的理论接触线分布(接触应力)如图2所示,接触齿号用1,2,…,5表示,各齿的一次接触区和二次接触线(区)分别用Ⅰ和Ⅱ表示。
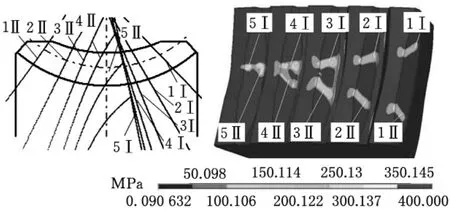
图2 蜗轮齿面接触线分布图
2 计算结果分析
笔者建立了多组有限元模型,用于分析载荷和主要齿形参数对齿面接触应力分布和齿间载荷分配系数的影响,以及包容齿数和啮合位置对最大齿间载荷分配系数的影响。
2.1 载荷的影响
2.1.1 载荷对齿间载荷分配比的影响
以中心距a=125mm、传动比i=63、转速为1500r/min时额定输出扭矩T2=1246N·m的蜗杆副为例,施加不同的载荷,研究齿间载荷分配系数的变化趋势,并用均方差考察齿间载荷分配的平均程度。均方差f的计算公式如下:

式中,ei为第i颗齿承受的载荷分配比:为齿间载荷分配比平均值;n为包容齿数。
载荷对齿间载荷分配比的影响如表1所示。根据表1,载荷较小时,靠近啮入端的三对齿承受大部分载荷,随着扭矩的增大,啮入端承受载荷减小,啮出端轮齿承受载荷不断增大,最大齿间载荷分配系数不断下降,均方差值不断减小,齿间载荷分配趋于均匀。

表1 载荷对齿间载荷分配比的影响
2.1.2 载荷对齿面应力分布的影响
传统的蜗杆接触应力计算公式中接触应力与载荷的0.5次方成正比[9],即

式中,T2为输出扭矩;ZE为材料系数;ZP为蜗杆传动系数;KA为工况系数。
图3所示是同一模型施加不同载荷下的齿面接触应力和一次区量化处理后的接触应力曲线,据此分析轮齿沿接触线方向应力分布随载荷的变化规律。

图3 载荷对齿面接触应力的影响
在传统的计算中,认为载荷沿接触线是平均分布的,分析图3,受轮齿形状影响,接触应力沿接触线从蜗轮齿根到齿顶呈“L”形分布,蜗轮的齿根发生了较明显的应力集中。对接触线中段上的应力进行平均处理,施加载荷比为0.50∶1.10∶1.50时第三对齿上一次接触区所承受的扭矩比是1∶1.8∶2.4,对应的接触应力比为1.00∶1.51∶1.78。
2.2 齿形参数对应力分布的影响
2.2.1 基圆直径的影响分析
建立蜗杆副有限元分析模型并施加相同的边界条件和载荷,改变基圆直径db,分析db对接触应力分布状态和齿间载荷分配比的影响。根据式(1)计算齿间载荷分配系数的均方差,分析db对载荷分配系数均匀度的影响。
如表2所示,随着db的增大,最大齿间载荷分配系数在31.5%~33.6% 之间变化,大部分载荷由靠近啮入端的3对齿承受。

表2 db对齿间载荷分配比的影响
根据图4,施加相同的扭矩,以二次接触区为例比较不同db时受载最大的一个齿的接触应力的分布状态。当db为71mm、94mm时,接触应力较大,且沿接触线呈“U”形分布;当db为80mm时,蜗轮齿面的接触应力最小,且分布均匀。
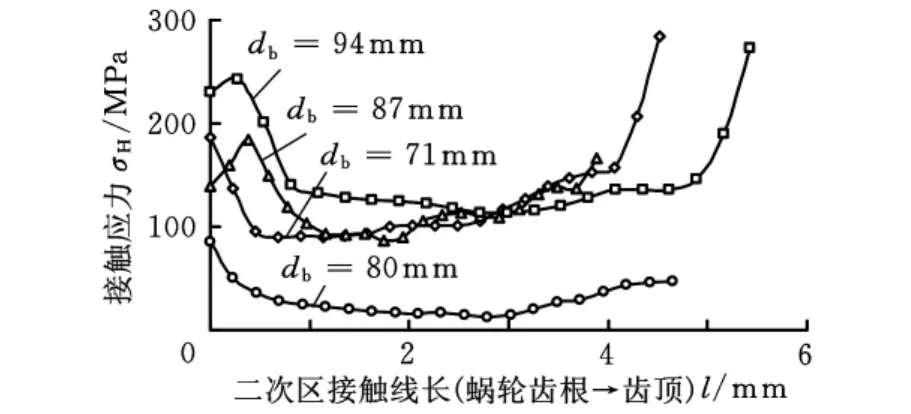
图4 db对接触应力的影响
2.2.2 母平面倾角β的影响
施加相同的载荷和边界条件,分析β对接触应力分布状态和齿间载荷分配比的影响。
如表3所示,随着β的变化,最大齿间载荷分配系数约在31.7%~37.1% 之间变化,β为1°时,齿面上只有一次接触线,均方差值最低,故齿间载荷分配最为均匀;β分别为4°、8°时,齿面上既有一次接触线,也存在二次接触线,两者均方差值相差不大。
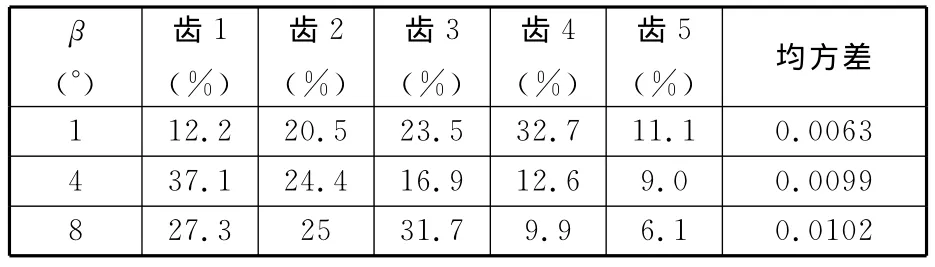
表3 β对齿间载荷分配比的影响
根据图5,施加相同的扭矩,比较β取不同值时受载最大的一个齿的接触应力的分布状态。随着β的增大,接触应力不断减小。

图5 β对接触应力的影响
综上所述,db对齿面接触应力分布状态的影响较大,选取合理的db,可避免齿根、齿顶应力集中。β对齿间载荷分配系数的影响较大,不同β对应的最大齿间载荷分配系数波动范围约5.4%。各组接触应力的对比分析表明,以应力均化为目的的参数优化可通过对比有限元分析结果完成。
2.3 包容齿数与最大齿间载荷分配系数的关系
包容齿数是指同时啮合的齿对数,笔者分别建立了包容齿数n为3、5、7时的接触分析模型,分析包容齿数对最大齿间载荷分配系数的影响。为了减小由于接触状态不同而产生的误差,各模型的接触状态基本一致(图2),即各模型的前n-1个齿的二次接触线在齿高方向的投影穿越全齿高,第n个齿的二次接触线在齿高方向的投影约为全齿高的50%。
如图6所示,在额定扭矩下包容齿数为3、5、7时对应的最大齿间载荷分配系数分别是46.5%、28.1%和24.8%。
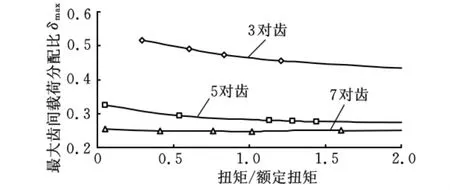
图6 包容齿数与最大齿间载荷分配系数的关系
包容齿数并不是一个固定不变的量,随着啮合时刻的不同,包容齿数总是在某个范围内周期性地变化。以包容齿数5为例,施加额定扭矩,考察一个啮合周期内啮合位置对最大齿间载荷分配系数的影响。
如图7所示,在蜗轮转过一个齿距角的周期内,包容齿数在5~6个齿内变化:最大齿间载荷分配系数在20.9%~26%之间变化。
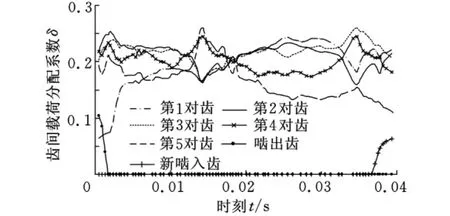
图7 啮合位置对齿间载荷分配系数的影响(转速为1500r/min)
3 结语
(1)分析了载荷、齿形参数对齿间载荷分配系数和齿面接触应力分布的影响;接触应力沿接触线呈“L”或“U”形分布。齿形参数对应力分布状态的影响不容忽略:选取合理的db,可有效避免齿根、齿顶应力集中;优化β角可有效减小最大齿间载荷分配系数,均化齿间载荷分配。
(2)研究了各级载荷下,包容齿数与最大齿间载荷分配系数的对应关系;并以5对齿啮合为例,分析了一个啮合周期内,不同啮合时刻最大齿间载荷分配系数约在20.9%~26%之间变化。
[1] 周良庸.环面蜗杆副疲劳强度的校核[J].机械工程学报,2004,40(9):180-184.
[2] 徐戊娇.制造误差与承载变形耦合条件下平面二次包络环面蜗杆的啮合分析与啮合控制研究[D].重庆:重庆大学,2005.
[3] Simon V.Stress Analysis in Double Enveloping Worm Gears by Finite Element Method[J].Journal of Mechanical Design,Transactions of the ASME,1993,115(3):179-185.
[4] 唐进元,蒲太平.弧齿锥齿轮动态啮合有限元数值分析[J].机械科学与技术,2009,28(8):981-985.
[5] 邓效忠,方宗德,杨宏斌,等.高重合度弧齿锥齿轮的强度分析[J].航空动力学报,2002,17(3):367-372.
[6] 朱才朝,黄琪,唐倩.风力发电升速齿轮箱传动系统接触齿数及载荷分配[J].农业机械学报,2006,37(7):86-89.
[7] 屈文涛,沈允文,郭辉,等.双圆弧齿轮的有限元综合分析方法[J].机械强度,2006,28(3):415-418.
[8] ANSYS Inc..ANSYS User’s Guide[M].Houston:ANSYS Inc.,2003.
[9] 齿轮手册编委会.齿轮手册(上册)[M].北京:机械工业出版社,1990.
Analysis on Stress Distribution and Influencing Factors of Planar Double Enveloping Hourglass Wom Gears
Zhang Yanqin Zhang Guanghui
State Key Laboratory of Mechanical Transmission,Chongqing University,Chongqing,400030
Based on the elastoplasticity contact finite element theory,a multi-group static and dynamic contact stress analysis models suitable for the worm gears were established.The influences of the load and parameters on the coefficient of load sharing among teeth and contact stress distribution were studied.The relationship between the number of teeth in the meshing and the maximum coefficient of load sharing among teeth under different loads was calculated.The results indicate:the load distribution tends to be even along with load enlargement;the contact stress distribution along the contact line like“L”or“U”;the influence of parameters on the stress can not be neglected,it is feasible that parameter optimized aimed at stress hypodispersion by contrasting the finite element analysis results.Under 0.05~1.5times the rated torque,the maximum coefficients of load sharing among the teeth are obtained when the number of meshing teeth is 3,5,7respectively.
worm gear;finite element method;stress;load sharing amongteeth
TH132.4
1004—132X(2011)10—1135—04
2010—07—23
国家自然科学基金资助项目(50075089)
(编辑 袁兴玲)
张彦钦,女,1980年生。重庆大学机械传动国家重点实验室博士研究生。主要研究方向为机械传动。张光辉,男,1937年生。重庆大学机械传动国家重点实验室教授、博士研究生导师。

