奇数齿数圆柱齿轮齿顶尺寸的计算探讨
陈 林
(南京高速齿轮制造有限公司,江苏 南京 211123)
齿轮是一种常见的机械传动件,被广泛使用在各种机械设备中。通过齿轮副的啮合运动实现力和运动的传递。一个齿轮副中的两齿轮齿数往往满足互质的条件,以使得啮合的机会更均等,通常相啮合两齿轮的齿数会存在奇数齿的情况。而齿顶圆直径作为齿轮件加工制造过程需要控制的参数,会影响到齿轮副的重合度以及实际顶隙,通常加以公差约束,甚至会作为产品的终检尺寸来要求。这就需要加工过程对尺寸的控制更为精准,从制造过程来看,奇数齿数由于无法直接测量齿顶圆直径,可行的是将齿顶圆直径换算成齿顶圆最大弦长,用量具直接检测齿顶圆最大弦长。常用且易于操作的方法就是采用游标卡尺或者外径卡尺来直接检测尺寸。加工时通过控制该尺寸来间接地保证齿顶圆直径达到设计要求,尤其是在齿形已加工好的零件再加工齿顶圆的情形就只能采用间接法保证齿顶圆尺寸的准确性。那么,尺寸转化计算的准确性就显得至关重要。
1 齿顶最大弦长的计算
关于齿顶圆最大弦长的计算公式,查阅文献及生产使用情况,常用的是便于现场计算的近似公式,如下
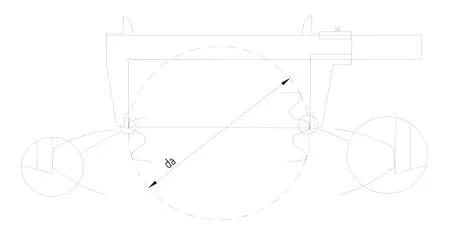
图2 奇数齿数齿顶圆尺寸的检测示意图
经过仔细推敲分析并结合生产实践,会发现上述公式计算不准确或者不符合实际检测条件,因为测量时,卡尺的卡爪间并不能准确保证正好落在齿顶正中心位置,多次可能会得到差异较大的一系列检测值,存在较大的测量误差,实现齿顶圆直径尺寸的控制。然而,最大值从理论上及实际测量时通过两卡爪跨过相对两齿顶的棱线,如图2 所示。从理论上该值是唯一的,生产现场实际检测也可以较容易地实现,测量系统性误差较小。
由图2 可知,齿顶圆最大弦长计算公式为
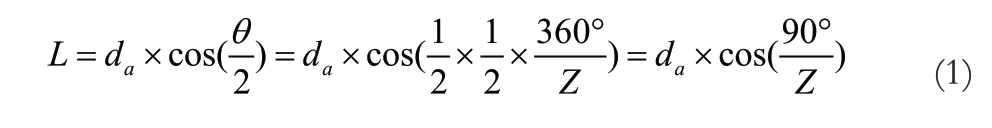
式中:ad 为齿顶圆直径,Z 为齿数(是一个奇数)。
上述近似公式可以通过图1 所示的几何关系得到。

图1 齿顶圆最大弦长近似表达
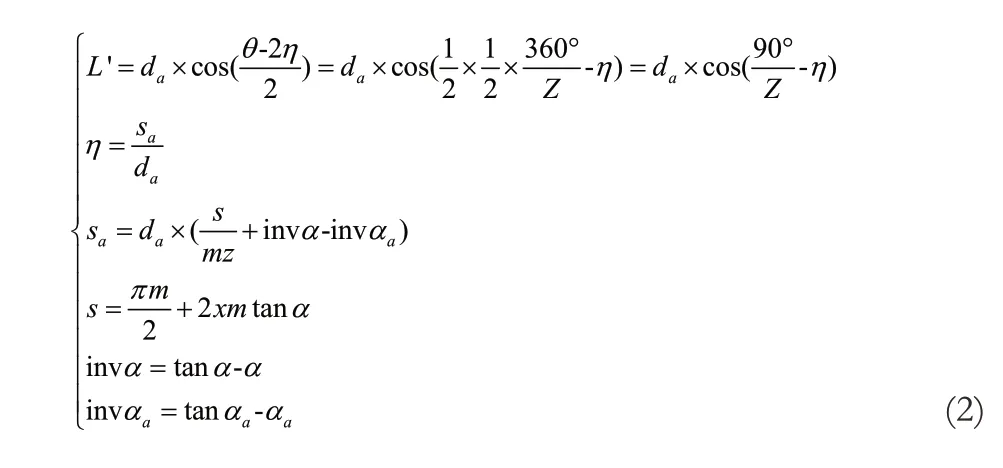
áa为齿顶圆端面压力角。

图3 齿顶圆最大弦长示意图
对比上述两种计算公式,精确计算公式需要计算齿顶圆齿厚,相比之下简化版公式则较为简单,方便生产现场在没有专门的计算工具的条件下使用,下面对简化版公式及精确计算两种公式进行简要的对比分析,考虑齿数对简化版公式结果准确性的影响。以便于在误差能够接受的范围内合理地选择公式,做到“又快又准”。从直观上看齿数越少两者差异越大,两者的差异体现在是否考虑了齿顶圆齿厚对应圆心角影响,如图3 所示。
2 计算误差分析
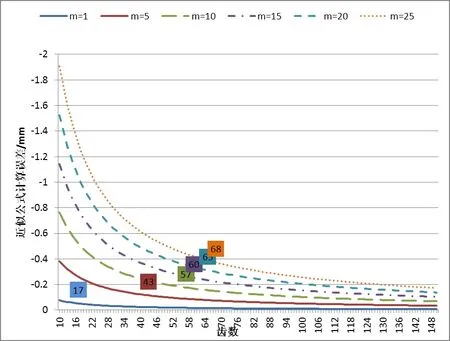
图4 近似计算公式误差
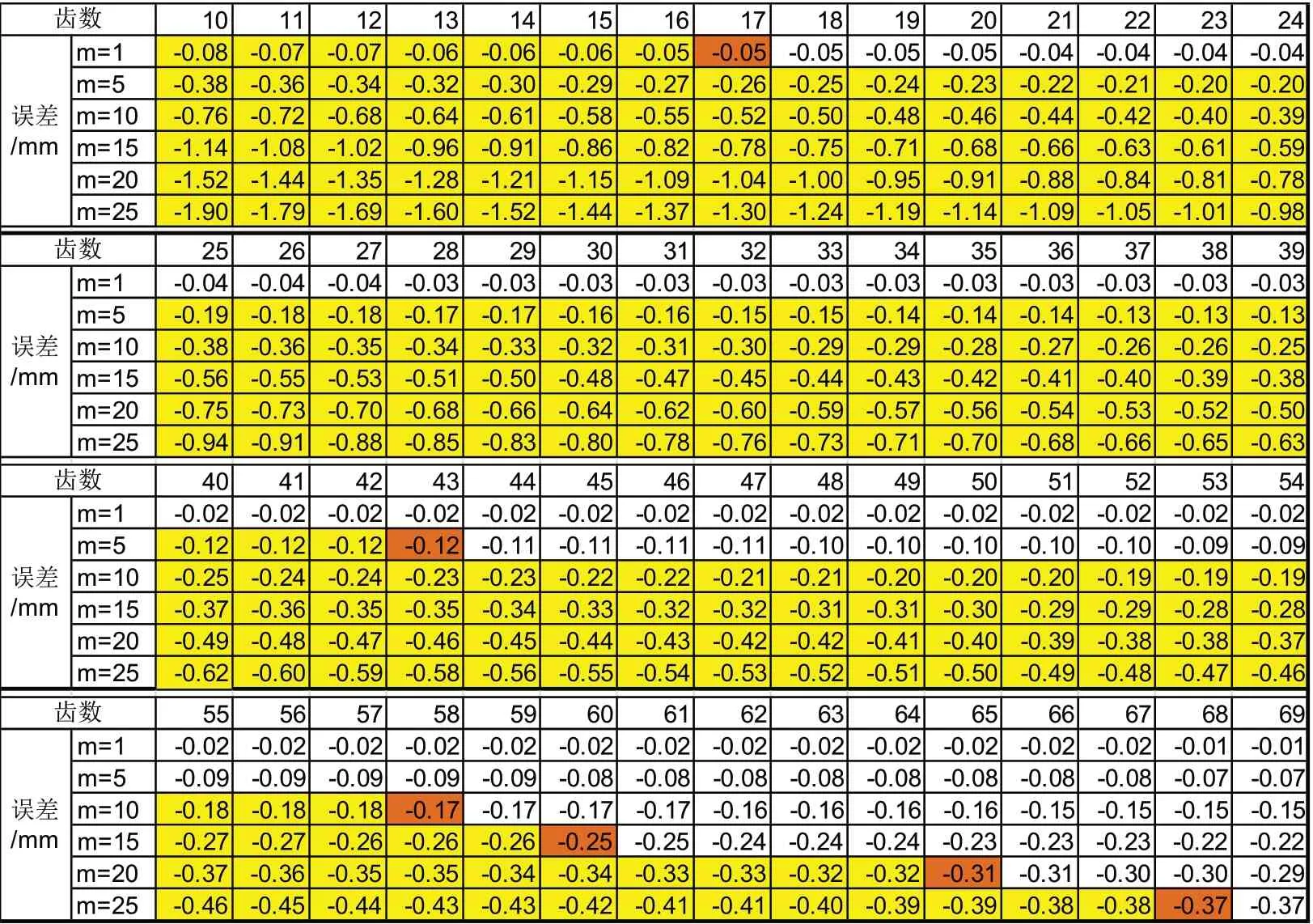
表1 近似计算公式误差表
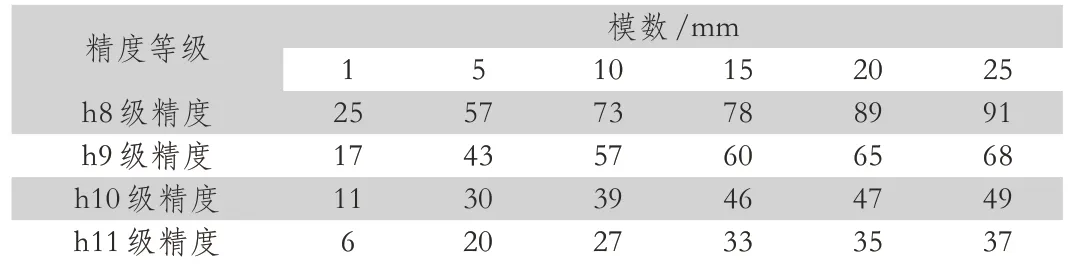
表2 各精度等级及模数对应临界齿数
根据计算结果,可得到如表2所示不同模数各精度等级对应的临界齿数,当齿数大于该临界值时,相应的齿轮件采用近似公式控制的齿顶圆尺寸能够达到相对应的精度等级。由图4可见,随着模数的增加,近似计算公式更易导致齿顶圆尺寸超差;如对于齿顶圆直径尺寸要求h9级的齿轮件,理论上能保证尺寸落在公差带内相对应模数1,5,10,15,20及25的临界齿数分别为17,43,57,60,65和68,如图4及表2。也就是模数为5的齿轮当其齿数不少于43时,按照近似公式结果加工的齿轮件能够使齿顶圆达到h9级公差要求内,模数为10的齿轮件当其齿数不少于57时,按照近似公式结果加工的齿轮件能够使齿顶圆达到h9级公差以内。
3 结论
近似公式的计算误差与齿轮件的齿数及模数相关。相同模数条件下随着齿数的增加误差逐渐减小,齿数增加至临界齿数以上时,计算误差会减小至相应公差等级要求的误差以内;对齿数较大的齿轮,计算误差相对较小,能够满足精度要求,而对齿数较少的齿轮件则可能会使得齿顶圆尺寸超差;随着模数的增加,临界齿数呈现出逐渐增加的趋势,对公式计算精确性要求更高。

